PageRank算法c++实现
首先用邻接矩阵A表示从页面j到页面i的概率,然后根据公式生成转移概率矩阵
M=(1-d)*Q+d*A 常量矩阵Q=(qi,j),qi,j=1/n
给定点击概率d,等级值初始向量R0,迭代终止条件e;
计算Ri+1=M*Ri;
ei=|Ri+1-Ri|,当ei<=e时输出Ri+1作为最终等级值向量。
#include "fstream"
#include "sstream"
#include <iostream>
#include <set>
#include <vector>using namespace std;int getNum()
{set<int> N;ifstream is("a.txt");int u, v;while (is >> u >> v){N.insert(u);N.insert(v);}return N.size();
}void getPage(vector<vector<int>>& page) //&
{ifstream is("a.txt");int u, v;while(is>>u>>v){ page[u].push_back(v);}
}void PageRank(vector<vector<int>>&page,int N,double d,double e,int maxIterations)
{//得到Mvector<vector<double>> M(N,vector<double>(N,0.0));for (int i = 0; i < N; i++){if (page[i].size() > 0){for (int j : page[i]){M[j][i]++; //0/1}for (int j=0;j<N;j++){M[j][i] /= page[i].size();}}else{for (int j : page[i]){M[j][i] = 0;}}}for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){//cout << M[i][j]<<" "; //正确M[i][j] = d * M[i][j] + (1 - d) * (1.0 / N);//cout << M[i][j] << " ";}}vector<double> pagerank(N, 1.0);while (maxIterations){vector<double> newpagerank(N, 0.0);double dif=0.0;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){newpagerank[i] += M[i][j] * pagerank[j];}dif+= abs(pagerank[i]-newpagerank[i]);}//cout << dif << endl;pagerank = newpagerank;if (dif < e){//cout << maxIterations<<endl;break;}maxIterations--;}cout << "等级值分别为:" << endl;for (int i = 0; i < N; i++){cout << pagerank[i]<<endl;}
}int main()
{int num = getNum();vector<vector<int>> page(num);getPage(page);double d = 0.85;double e = 0.1;int maxIterations = 100;PageRank(page, num, d, e, maxIterations);}数据
0 1
0 2
0 3
1 0
1 2
2 3
3 0
3 1
结果

相关文章:

PageRank算法c++实现
首先用邻接矩阵A表示从页面j到页面i的概率,然后根据公式生成转移概率矩阵 M(1-d)*Qd*A 常量矩阵Q(qi,j),qi,j1/n 给定点击概率d,等级值初始向量R0,迭代终止条件e; 计算Ri1M*R…...
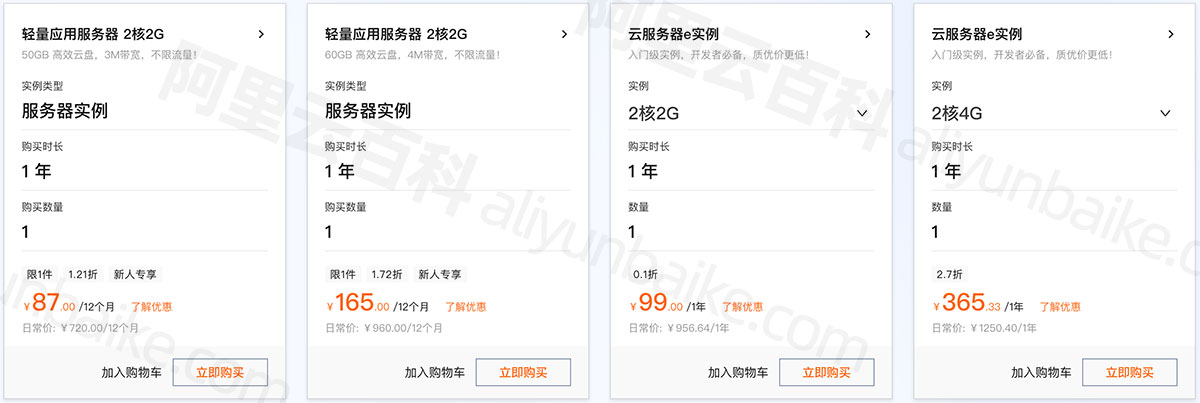
超低价:阿里云双11服务器优惠价格表_87元一年起
2023阿里云双十一优惠活动已经开启了,轻量2核2G服务器3M带宽优惠价87元一年、2核4G4M带宽优惠价165元一年,云服务器ECS经济型e实例2核2G3M固定带宽优惠价格99元一年,还有2核4G、2核8G、4核8G、4核16G、8核32G等配置报价,云服务器e…...

docker的安装Centos8
在CentOS 7中,可以使用yum安装Docker。Docker官方提供了一个yum源,可以用于安装Docker。以下是安装Docker的步骤: 卸载旧版本的Docker(如果有) 如果你之前安装过Docker,需要先卸载旧版本的Docker。执行以…...

Android.mk文件制定了链接库,但是出现ld Error
问题描述 Android.mk文件中,指定了库: LOCAL_LDLIBS : -lmylib LOCAL_LDFLAGS -L$(MYLIB_DIR)/lib出现ld: error: undefined symbol: my_function,于是查看so里面是否有my_function函数: nm -D libmylib.so | grep my_functio…...
10.MySQL事务(上)
个人主页:Lei宝啊 愿所有美好如期而遇 目录 前言: 是什么? 为什么? 怎么做? 前言: 本篇文章将会说明什么是事务,为什么会出现事务?事务是怎么做的? 是什么? 我…...

nexus搭建npm私有镜像
假设有一个nexus服务,地址为: http://10.10.33.50:8081/ 创建存储空间 登录后创建存储空间,选择存储类型为File,并设置空间名称为 npm-private 创建仓库类型 2.1 创建hosted类型仓库 创建一个名为 npm-hosted 的本地类型仓库 2.…...

智能化的宠物喂食器解决方案
随着经济条件的不断改善,越来越多的家庭开始追求生活的便捷享受,于是喂食器开始走进千家万户,喂食器主要由储存食物的蓄食箱和传送食物的滑道构成,在外部框架的支撑下,一台喂食器才能正常进行工作,而宠物喂…...
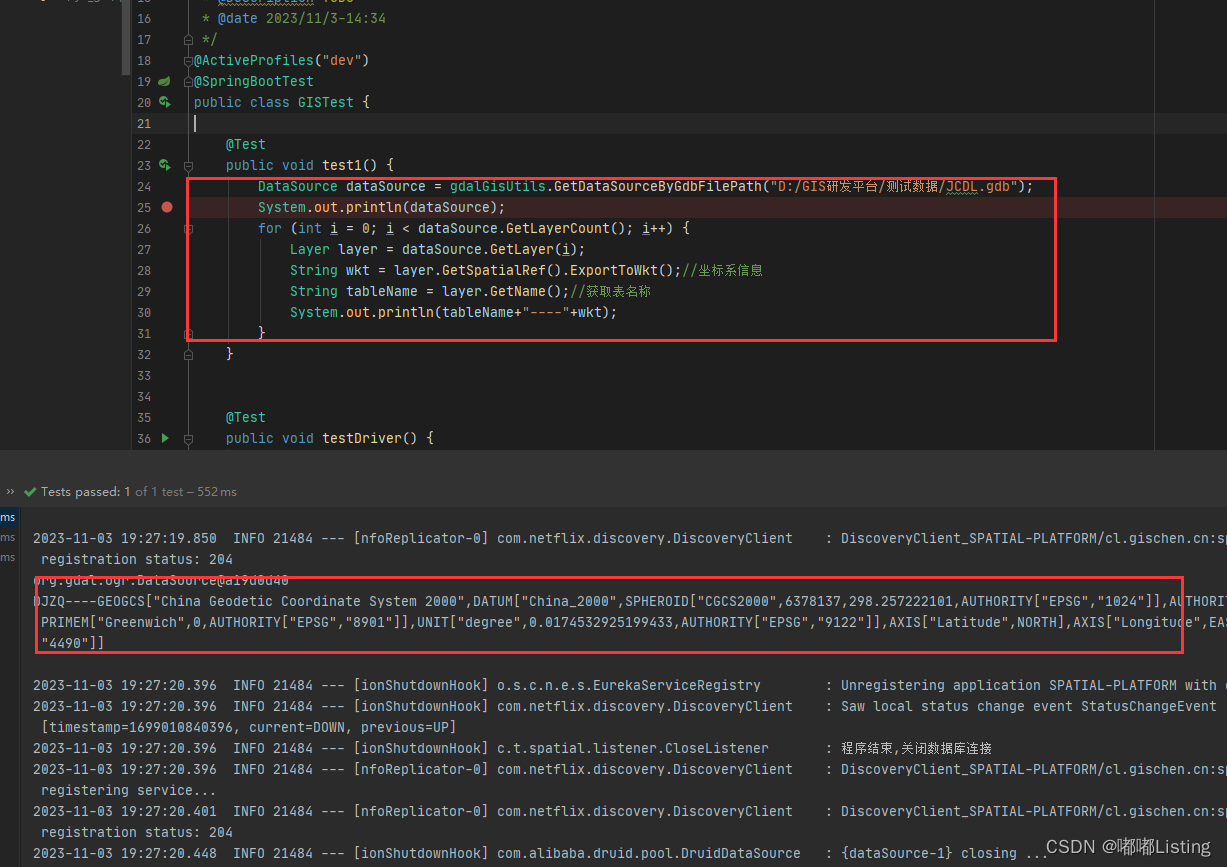
java配置GDAL
<gdal.version>3.7.0</gdal.version><!-- gdal--><dependency><groupId>org.gdal</groupId><artifactId>gdal</artifactId><version>${gdal.version}</version></dependency> GDAL环境安装 downlo…...

采购对接门禁系统采购进厂 空车出厂
本人详解 作者:王文峰,参加过 CSDN 2020年度博客之星,《Java王大师王天师》 公众号:山JAVA开发王大师,专注于天道酬勤的 Java 开发问题中国国学、传统文化和代码爱好者的程序人生,期待你的关注和支持!本人外号:神秘小峯 山峯 转载说明:务必注明来源(注明:作者:王文…...

服务器经常被攻击的原因
很多中小型企业都是选择虚拟主机服务器,是把一个服务器分成很多个给很多企业一起共用,可能同一个 IP服务器上就有很多个不同企业的网站,这个时候如果跟你同一个IP服务器的网站遭到DDoS攻击,就很有可能会影响到你的网站也无法正常访…...

子女购买房屋,父母出资的如果父母有关借贷的举证不充分则应认定该出资为赠与行为
现实生活中,由于父母与子女不和、子女离婚时父母为保全自己的出资等原因还经常会出现父母请求返还出资的情形。从司法实践反馈情况来看,父母请求返还出资所主张的基础法律关系往往为借贷而非赠与。基干父母子女之间密切的人身财产关系,父母出…...
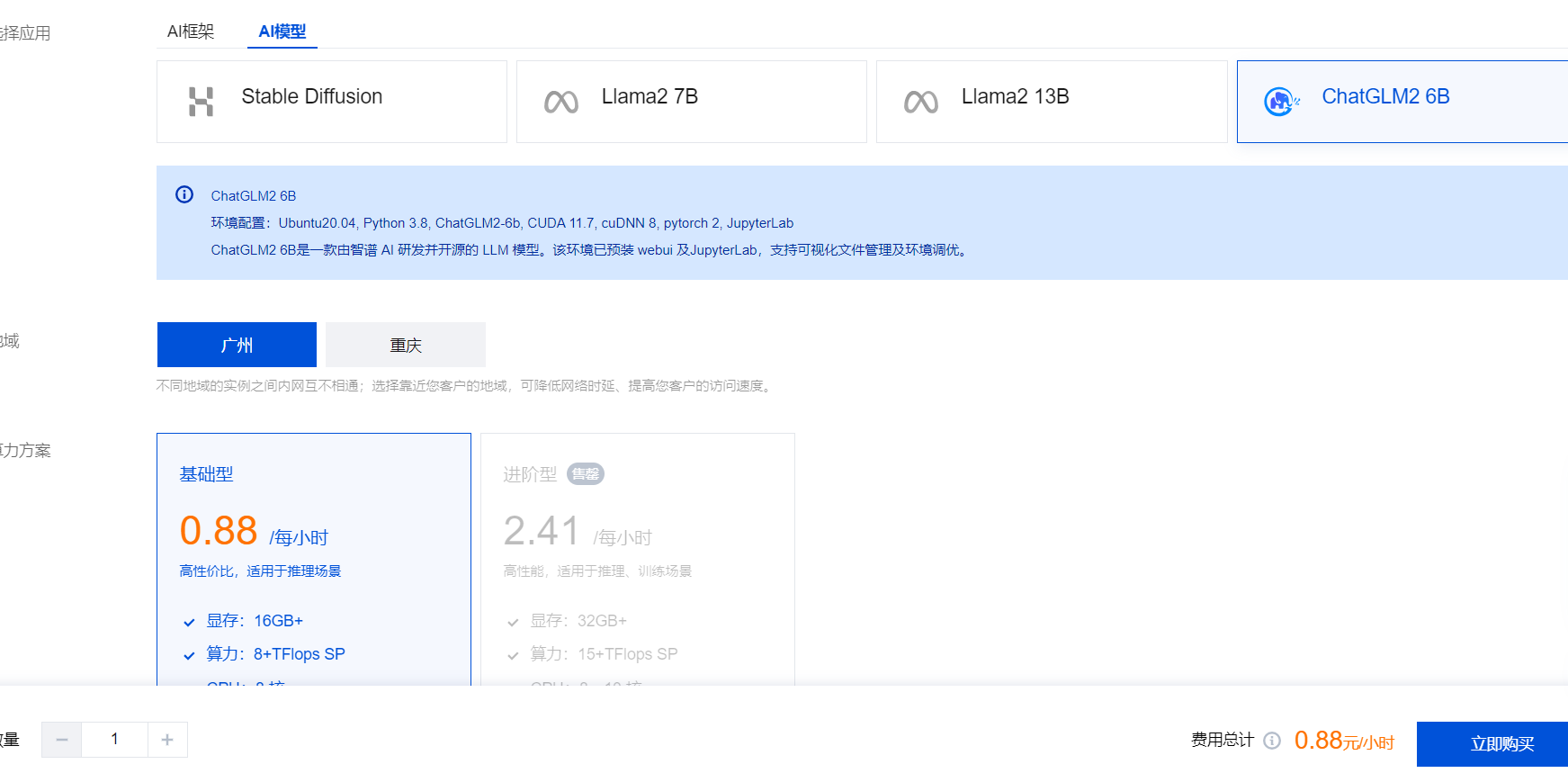
【腾讯云HAI域探秘】速通腾讯云HAI
速览HAI 产品简介 腾讯云高性能应用服务(Hyper Application lnventor,HA),是一款面向 Al、科学计算的 GPU 应用服务产品,为开发者量身打造的澎湃算力平台。无需复杂配置,便可享受即开即用的GPU云服务体验。在 HA] 中,…...

R语言爬虫代码模版:技术原理与实践应用
目录 一、爬虫技术原理 二、R语言爬虫代码模板 三、实践应用与拓展 四、注意事项 总结 随着互联网的发展,网络爬虫已经成为获取网络数据的重要手段。R语言作为一门强大的数据分析工具,结合爬虫技术,可以让我们轻松地获取并分析网络数据。…...

行业观察:数字化企业需要什么样的数据中心
伴随着数字经济在中国乃至全球的高速发展,数字化转型已经成为广大企业的必经之路。而作为数字经济的核心基础设施,数据中心充当了接收、处理、存储与转发数据流的“中枢大脑”,对驱动数字经济发展和企业数字化转型起到了极为关键的重要作用。…...

PHP依赖注入 与 控制反转详解
依赖注入 是一种设计模式,用于解耦组件之间的依赖关系。 它的主要思想是通过将依赖的对象传递给调用方,而不是由调用方自己创建或管理依赖的对象。这种方式使得组件的依赖关系更加灵活,易于维护和测试。 控制反转 是一个更广泛的概念&#…...

算法:Java构建二叉树并迭代实现二叉树的前序、中序、后序遍历
先自定义一下二叉树的类: // Definition for a binary tree node. public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val val;this.left…...

大数据毕业设计选题推荐-旅游景点游客数据分析-Hadoop-Spark-Hive
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...
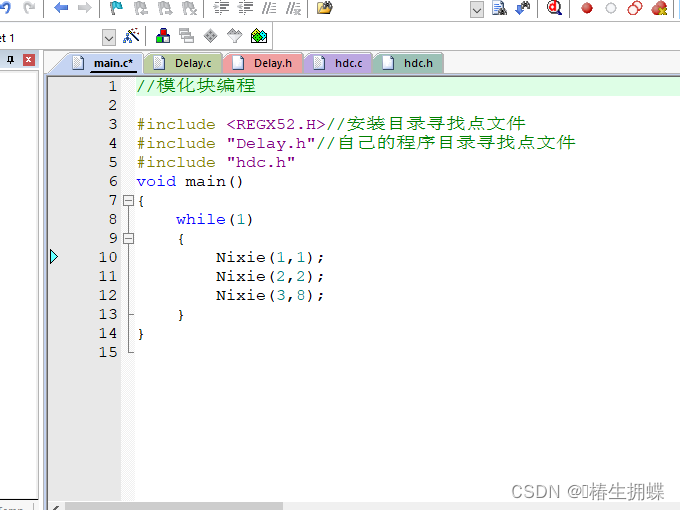
单片机,0.06
...

[PyTorch][chapter 59][强化学习-2-有模型学习]
前言: 在已知模型的环境里面学习,称为有模型学习(model-based learning). 此刻,下列参数是已知的: : 在状态x 下面,执行动作a ,转移到状态 的概率 : 在状态x 下面,执行动作a ,转移到 的奖赏 有模型强化学习的应用案例 …...
【接口测试】HTTP接口详细验证清单
概述 当我们在构建、测试、发布一套新的HTTP API时,包括我在内的大多数人都不知道他们所构建的每一个组件的复杂性和细微差别。 即使你对每一个组件都有深刻的理解,也可能会有太多的信息在你的脑海中出现。 以至于我们不可能一下把所有的信息进行梳理…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
