[PyTorch][chapter 59][强化学习-2-有模型学习]
前言:
在已知模型的环境里面学习,称为有模型学习(model-based learning).
此刻,下列参数是已知的:
: 在状态x 下面,执行动作a ,转移到状态
的概率
: 在状态x 下面,执行动作a ,转移到
的奖赏


有模型强化学习的应用案例
棋类游戏:有模型强化学习算法(例如MCTS)被广泛应用于棋类游戏,例如围棋、国际象棋等。AlphaGo和AlphaZero就是使用MCTS的典型例子。
路径规划:有模型强化学习算法(例如动态规划)可以用于路径规划问题,例如机器人导航、无人机路径规划等。
资源调度:有模型强化学习算法可以用于优化资源调度问题,例如数据中心的任务调度、物流配送的路径规划等
目录:
- 策略评估
- Bellman Equation
- 基于 T步累积奖赏的策略评估算法 例子
一 策略评估
模型已知时,对于任意策略,能估算出该策略带来的期望累积奖赏。
假设:
状态值函数: : 从状态x 出发,使用策略
,带来的累积奖赏
状态-动作值函数 : 从状态x 出发,执行动作a,再使用策略
,带来的累积奖赏
由定义:
状态值函数为:
: T 步累积奖赏
:
折扣累积奖赏,
状态-动作值函数
T 步累积奖赏
折扣累积奖赏
由于MDP具有马尔可夫性,即现在决定未来,将来和过去无关,我们很容易找到值函数的递归关系(Bellman 等式)
2.2 r折扣累积奖赏
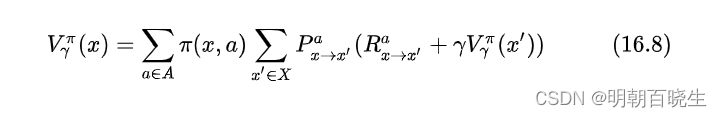
这是一种动态规划方案,从 出发,通过一次迭代就能计算出每个状态的单步累积奖赏
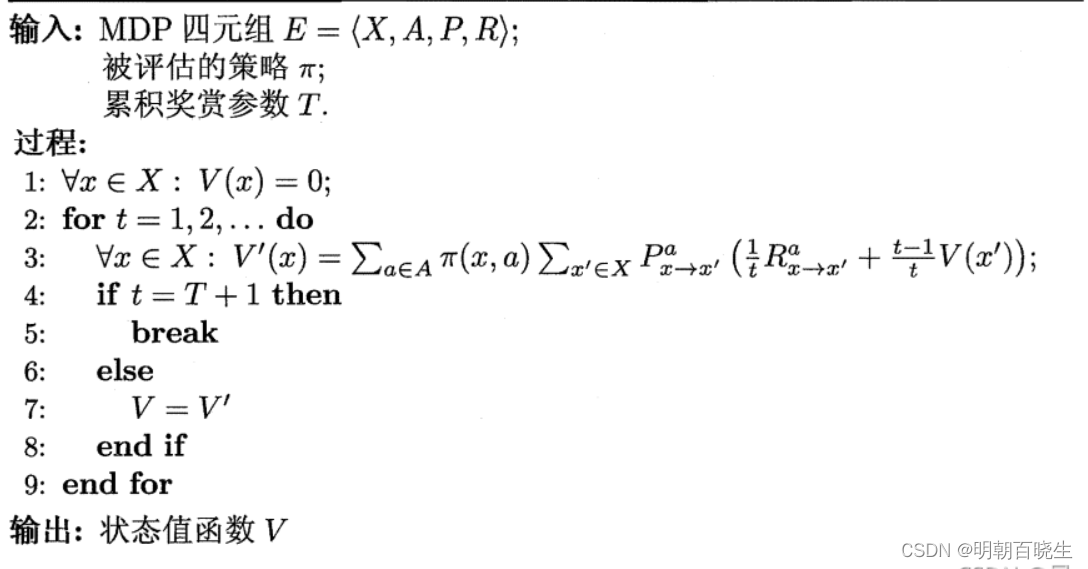
有了状态值函数V后,可以直接计算出状态-动作值函数:

由于算法可能会迭代很多次,可以设置一个阀值,当执行一次迭代后
函数值小于,停止迭代
二 Bellman Equation(贝尔曼方程)


2.1 Summing all future rewards and discounting them would lead to our return G
2.2 state-value function
给定策略 时,基于 state s 的条件期望函数,公式表示为:
State-value function can be broken into:
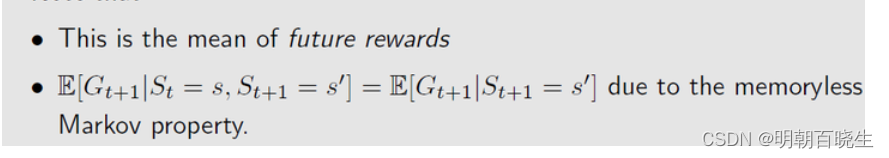

三 基于 T步累积奖赏的策略评估算法 例子
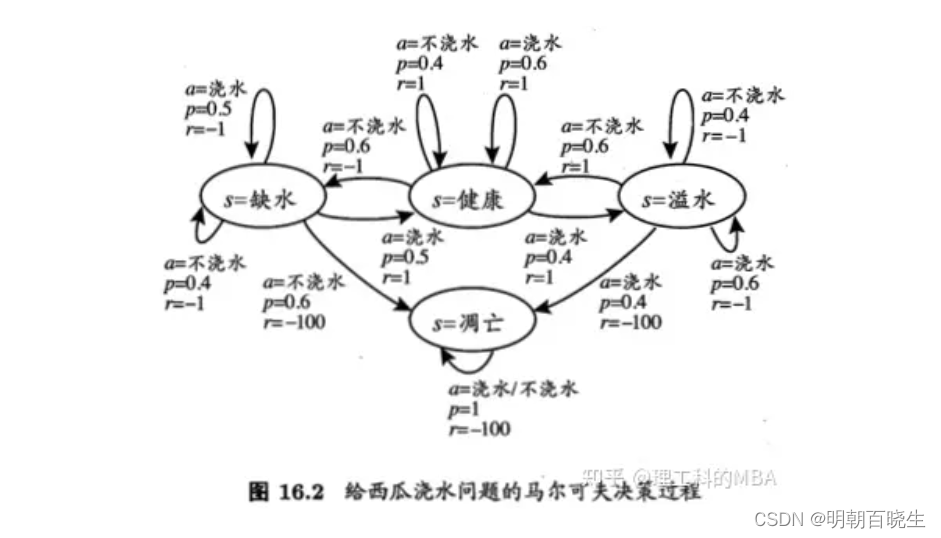
代码里面的行为函数采用的是Stochastic

# -*- coding: utf-8 -*-
"""
Created on Mon Oct 30 15:38:17 2023@author: chengxf2
"""
import numpy as np
from enum import Enumclass State(Enum):#状态空间X shortWater =1 #缺水health = 2 #健康overflow = 3 #凋亡apoptosis = 4 #溢水class Action(Enum):#动作空间Awater = 1 #浇水noWater = 2 #不浇水class Env():def __init__(self):#状态空间self.X = [State.shortWater, State.health,State.overflow, State.apoptosis] #动作空间self.A = [Action.water,Action.noWater] self.Q ={}#从状态x出发,执行动作a,转移到新的状态x',得到的奖赏 r为已知道self.Q[State.shortWater] =[[Action.water,0.5, State.shortWater,-1],[Action.water,0.5, State.health,1],[Action.noWater,0.4, State.shortWater,1],[Action.noWater,0.6, State.overflow,-100]]self.Q[State.health] = [[Action.water,0.6, State.health,1],[Action.water,0.4, State.apoptosis,-1],[Action.noWater,0.6, State.shortWater,-1],[Action.noWater,0.4, State.health,1]]self.Q[State.overflow] = [[Action.water,0.6, State.overflow,-1],[Action.water,0.4, State.apoptosis,-100],[Action.noWater,0.6, State.health,1],[Action.noWater,0.4, State.overflow,-1]]self.Q[State.apoptosis] =[[Action.water,1, State.apoptosis,-100],[Action.noWater,1, State.apoptosis,-100]]def GetX(self):#获取状态空间return self.Xdef GetAction(self):#获取动作空间return self.Adef GetQTabel(self):return self.Qclass LearningAgent():def GetStrategy(self): #策略,处于不同的状态下面,采用不同的actionstragegy ={}stragegy[State.shortWater] = {Action.water:1.0, Action.noWater:0.0}stragegy[State.health] = {Action.water:0.9, Action.noWater:0.1}stragegy[State.overflow] = {Action.water:0.1, Action.noWater:0.9}stragegy[State.apoptosis] = {Action.water:0.0, Action.noWater:0.0}return stragegydef __init__(self):env = Env()self.X = env.GetX()self.A = env.GetAction()self.QTabel = env.GetQTabel()self.curV ={} #前面的累积奖赏self.V ={} #累积奖赏for x in self.X: self.V[x] =0self.curV[x]=0def GetAccRwd(self,state,stragegy,t,V):#AccumulatedRewards#处于x状态下面,使用策略,带来的累积奖赏reward_x =0.0for action in self.A:#当前状态处于x,按照策略PI,选择action 的概率,正常为1个,也可以是多个(按照概率选取对应的概率)p_xa = stragegy[state][action] # 使用策略选择action 的概率#任意x' in X, s下个状态QTabel= self.QTabel[state]reward =0.0#print("\n ---Q----\n",QTabel)for Q in QTabel:#print(Q, action)if Q[0] == action:#新的状态x'newstate = Q[2] #当前状态x,执行动作a,转移到新的状态s的概率p_a_xs = Q[1]#当前状态x,执行动作a,转移到新的状态s,得到的奖赏r_a_xs = Q[-1]reward += p_a_xs*((1.0/t)*r_a_xs + (1.0-1/t)*V[newstate])#print("\n 当前状态 ",x, "\t 转移状态 ",s, "\t 奖赏 ",r_a_xs,"\t 转移概率 ",p_a_xs ,"\t reward",reward)reward_x +=p_xa*rewardreturn reward_xdef learn(self,T):stragegy = self.GetStrategy()for t in range(1,T+1):#获得当前的累积奖赏for x in self.X:self.curV[x] = self.GetAccRwd(x,stragegy,t,self.V)if (T+1) == t:breakelse:self.V = self.curVfor x in self.X:print("\n 状态 ",x, "\t 奖赏 ",self.V[x])if __name__ == "__main__":T =100agent = LearningAgent()agent.learn(T)参考:
https://www.cnblogs.com/CJT-blog/p/10281396.html
1. 有模型强化学习概念理解_哔哩哔哩_bilibili
1.强化学习简介_哔哩哔哩_bilibili
16 强化学习 - 16.3 有模型学习 - 《周志华《机器学习》学习笔记》 - 书栈网 · BookStack
1 强化学习基础-Bellman Equation - 知乎
相关文章:

[PyTorch][chapter 59][强化学习-2-有模型学习]
前言: 在已知模型的环境里面学习,称为有模型学习(model-based learning). 此刻,下列参数是已知的: : 在状态x 下面,执行动作a ,转移到状态 的概率 : 在状态x 下面,执行动作a ,转移到 的奖赏 有模型强化学习的应用案例 …...
【接口测试】HTTP接口详细验证清单
概述 当我们在构建、测试、发布一套新的HTTP API时,包括我在内的大多数人都不知道他们所构建的每一个组件的复杂性和细微差别。 即使你对每一个组件都有深刻的理解,也可能会有太多的信息在你的脑海中出现。 以至于我们不可能一下把所有的信息进行梳理…...

ALLRGRO拼板的问题。
1、建议拼板还是用AUTO CAD或者CAM350会比较方便。 2、如果要在allegro中拼板,就拼个外框Outline,然后让板厂的人按照板框帮你放。板厂都会帮你操作的。也不会影响贴片。 3、如果非要死乞白赖的在PCB板子里面拼板,请看文章最后面。 具体的…...

YOLO算法改进6【中阶改进篇】:depthwise separable convolution轻量化C3
常规卷积操作 对于一张55像素、三通道(shape为553),经过33卷积核的卷积层(假设输出通道数为4,则卷积核shape为3334,最终输出4个Feature Map,如果有same padding则尺寸与输入层相同(…...
自定义类型枚举
目录 枚举类型枚举类型的声明扩展枚举类型的优点枚举的优点 感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接 🐒🐒🐒 个人主页 🥸🥸🥸 C语言 🐿️🐿️🐿…...

PHP foreach 循环跳过本次循环
$a [[id>1],[id>2],[id>3],[id>4],[id>5],[id>6],[id>7],[id>18],];foreach($a as $v){if($v[id] 5){continue;}$b[] $v[id];}return show_data(,$b); 结果:...

lua-web-utils库
lua--导入所需的库local web_utilsrequire("lua-web-utils")--定义要下载的URLlocal url"https://jshk.com.cn/"--定义代理服务器的主机名和端口号local proxy_port8000--使用web_utils的download函数下载URLlocal file_pathweb_utils.download(url,proxy_…...

大数据毕业设计选题推荐-热门旅游景点数据分析-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...
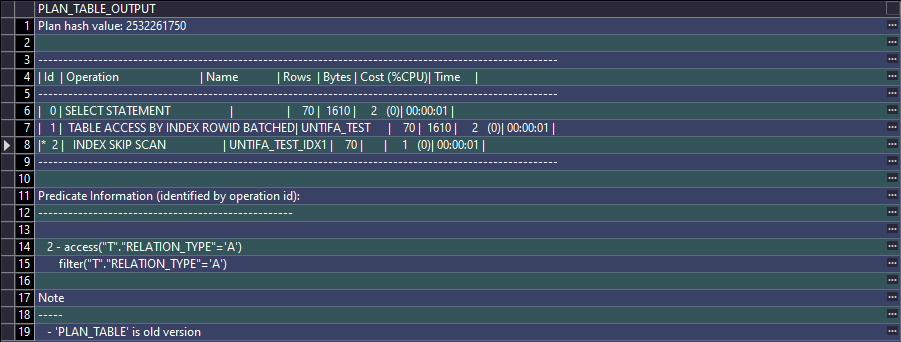
Oracle-执行计划
执行计划生成的几种方式 1. EXPLAIN FOR 语法: EXPLAIN PLAN FOR SQL语句SELECT * FROM TABLE(dbms_xplan.display());优点: 无需真正执行SQL 缺点: 没有输出相关的统计信息,例如产生了多少逻辑读、物理读、递归调用等情况无法判…...

Pytho入门教程之Python运行的三种方式
文章目录 一、交互式编程二、脚本式编程三、方式三关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③Python小游戏源码五、面试资料六、Python兼职渠道 一、交互式编…...

如何修改docker容器中的MySQL数据库的密码?
查看容器中MySQL的ID:docker ps | grep mysql进入容器:docker exec -it {容器ID} /bin/bash调整MySQL配置文件,设置跳过权限控制:echo "skip-grant-tables" >> /etc/mysql/conf.d/docker.cnf 警 告:这…...

JOSEF约瑟 数显三相电压继电器 HJY-931A/D 导轨安装
名称:数字交流三相电压继电器型号:HJY-93系列品牌:JOSEF约瑟电压整定范围:10~450VAC额定电压:200、400VAC功率消耗:≤5W HJY系列 数字交流三相电压继电器 系列型号 HJY-931A/D数字式交流三相电压继电器&am…...
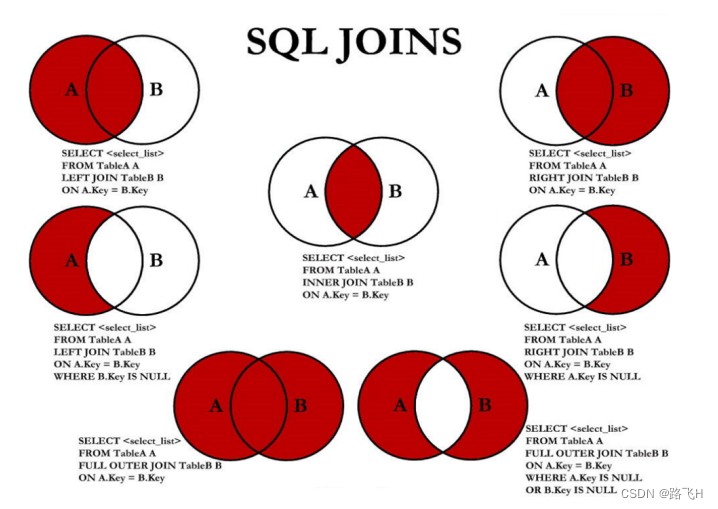
第6章_多表查询
文章目录 多表查询概述1 一个案例引发的多表连接1.1 案例说明1.2 笛卡尔积理解演示代码 2 多表查询分类讲解2.1 等值连接 & 非等值连接2.1.1 等值连接2.1.2 非等值连接 自连接 & 非自连接内连接与外连接演示代码 3 SQL99语法实现多表查询3.1 基本语法3.2 内连接&#x…...
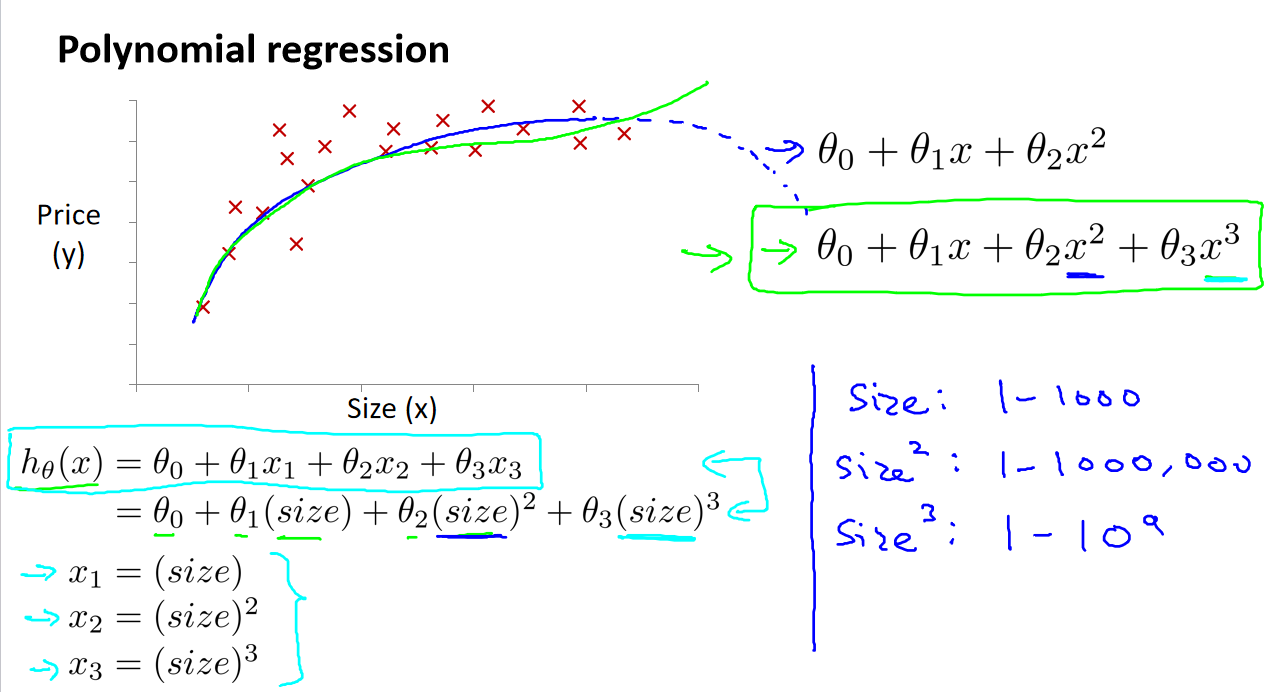
吴恩达《机器学习》4-1->4-5:多变量线性回归
一、引入多维特征 在多维特征中,我们考虑的不再是单一的特征,而是一组特征,例如房价模型中可能包括房间数、楼层等多个特征。这些特征将组成一个向量,表示为(𝑥₁, 𝑥₂, . . . , 𝑥ₙ)&#x…...

搜索引擎系统简要分析
目录 一、搜索引擎简单介绍 二、搜索引擎整体架构和工作过程 (一)整体分析 (二)爬虫系统 三个基本点 爬虫系统的工作流程 关键考虑因素和挑战 (三)索引系统 网页处理阶段 预处理阶段 反作弊分析…...

蓝桥杯(C++ 扫雷)
题目: 思想: 1、遍历每个点是否有地雷,有地雷则直接返回为9,无地雷则遍历该点的周围八个点,计数一共有多少个地雷,则返回该数。 代码: #include<iostream> using namespace std; int g[…...
--mobile - 蜂窝网络)
LuatOS-SOC接口文档(air780E)--mobile - 蜂窝网络
示例 -- 简单演示log.info("imei", mobile.imei()) log.info("imsi", mobile.imsi()) local sn mobile.sn() if sn thenlog.info("sn", sn:toHex()) end log.info("muid", mobile.muid()) log.info("iccid", mobile.icc…...

c++创建函数对象的不同方式
在C中,创建任何一个对象(即使我们创建的是一个没有任何成员变量的对象)时,需要占用一定的内存空间。 应用程序会将可用的内存(排除源代码运行的内存等)分出两个部分:栈(stack&#x…...
python实现从字符串中识别出省市区信息
从字符串中识别出省市区的信息分别存储,是我们经常会碰到的问题。如果用分词的方法去匹配获取比较麻烦,cpca包提供了便捷的调用函数transform。只要把含省市区的信息放进去,即可返回标准的含省市区的数据框。 本文详细阐述如何安装cpca包、transform函数参数定义,以及…...
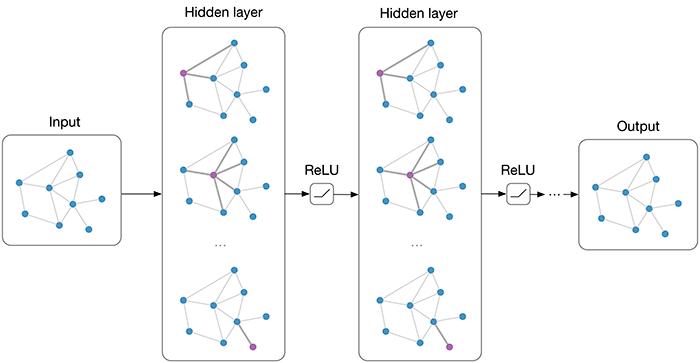
GCN火车票识别项目 P1 火车票识别项目介绍 Pytorch LSTM/GCN
从本节开始,我将带大家完成一个深度学习项目:用图卷积神经网络(GCN),实现一个「火车票文字信息提取」的项目,由于火车票上每个节点文字不是等长的,所以还需要添加一个前置的 LSTM 来提取句子特征。 课前说明 1、这是…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
