最长回文子串-LeetCode5 动态规划

由于基础还不是很牢固 一时间只能想到暴力的解法:
取遍每个子串 总数量n+n-1+n-2+…+1 =O(n^2)
判断每个子串是否属于回文串 O(n)
故总时间复杂度为O(n^3)
class Solution {
public:string longestPalindrome(string s) {
int max=0;string ret;for(int i=0;i<s.size();i++)for(int j=1;j<=s.size()-i;j++){string s1=s.substr(i,j);if(Judeg(s1)>max){max=Judeg(s1);ret=s1;}}return ret;}int Judeg(string s)
{int i,j;for(i=0,j=s.size()-1;i<=j;i++,j--){if(s[i]!=s[j])return 0;}return s.size();
}
};
在查阅题解以后 比较简单易懂的还是动态规划算法
设某子串的左下标为i 右下标为j
则该子串是不是回文串可以走如下流程:
1.s[i]和s[j]不相等 那么一定不是回文子串 dp[i][j]=false
2.在s[i]和s[j]已经相等的基础上 若子串的长度<=3 那么一定是回文串 dp[i][j]=true
3.最后一种情况 dp[i][j]=dp[i+1][j-1]
一个很长的子串是不是回文串 取决于去掉首尾字符以后 中间的子串是不是回文串(动态规划套娃)
时间复杂度为遍历dp数组 故为O(n^2)
空间复杂度为开辟dp数组 故为O(n^2)
string longestPalindrome(string s)
{int max=1,begin=0;int len=s.size();if(len<2)return s;bool **dp=new bool*[len];for(int i=0;i<len;i++){dp[i]=new bool [len];}for(int j=1;j<len;j++){for(int i=0;i<j;i++){if(s[i]!=s[j])dp[i][j]=false;else{if(j-i+1<=3)dp[i][j]=true;else{dp[i][j]=dp[i+1][j-1];}}if(dp[i][j]&&j-i+1>max){max=j-i+1;begin=i;}}}return s.substr(begin,max);
}
相关文章:

最长回文子串-LeetCode5 动态规划
由于基础还不是很牢固 一时间只能想到暴力的解法: 取遍每个子串 总数量nn-1n-2…1 O(n^2) 判断每个子串是否属于回文串 O(n) 故总时间复杂度为O(n^3) class Solution { public:string longestPalindrome(string s) { int max0;string ret;for(int i0;i<s.size();i)for(int…...

mysql简单备份和恢复
版本:mysql8.0 官方文档 :MySQL :: MySQL 8.0 Reference Manual :: 7 Backup and Recovery 1.物理备份恢复 物理备份是以数据文件形式备份。这种方式效率高点,适合大型数据库备份。物理备份可冷备可热备。 使用mysqlbackup 命令进行物理备…...

JMeter介绍
1. JMeter是什么? 是Apache组织开发基于Java的接口测试工具,性能测试工具 2.JMeter的优缺点 优点: 开源,免费 跨平台 支持多协议 轻量级别 缺点: 不支持IP欺骗 不可验证页面UI 3.JMeter可以用来做什么? …...

flink job同时使用BroadcastProcessFunction和KeyedBroadcastProcessFunction例子
背景: 广播状态可以用于规则表或者配置表的实时更新,本文就是用一个欺诈检测的flink作业作为例子看一下BroadcastProcessFunction和KeyedBroadcastProcessFunction的使用 BroadcastProcessFunction和KeyedBroadcastProcessFunction的使用 1.首先看主流…...

数据中心系统解决方案
设计思路 系统设计过程中充分考虑各个子系统的信息共享要求,对各子系统进行结构化和标准化设计,通过系统间的各种联动方式将其整合成一个有机的整体,使之成为一套整体的、全方位的数据中心大楼综合管理系统,达到人防、物防和技防…...
服务器开设新账户,创建账号并设置密码
实验室又进新同学了,服务器开设新账号搞起来 1、创建用户: 在root权限下,输入命令useradd -m 用户名,如下 sudo useradd -m yonghuming 2、设置密码: 输入命令passwd 用户名 回车,接着输入密码操作&…...

【C++】关于构造函数后面冒号“:“的故事------初始化列表(超详细解析,小白一看就懂)
目录 一、前言 二、 初始化的概念区分 三、初始化列表 (重点) 💦初始化列表的概念理解 💦初始化列表的注意事项 四、共勉 一、前言 在之前的博客学习中,我们已经学习了【C】的六大默认成员函数 ,想必大…...
)
【Shell 系列教程】shell基本运算符(四)
文章目录 往期回顾关系运算符布尔运算符逻辑运算符字符串运算符文件测试运算符其他检查符: 往期回顾 【Shell 系列教程】shell介绍(一)【Shell 系列教程】shell变量(二)【Shell 系列教程】shell数组(三&am…...

MongoDB安装及开发系例全教程
一、系列文章目录 一、MongoDB安装教程—官方原版 二、MongoDB 使用教程(配置、管理、监控)_linux mongodb 监控 三、MongoDB 基于角色的访问控制 四、MongoDB用户管理 五、MongoDB基础知识详解 六、MongoDB—Indexs 七、MongoDB事务详解 八、MongoDB分片教程 九、Mo…...
ffmpeg命令帮助文档
一:帮助文档的命令格式 ffmpeg -h帮助的基本信息ffmpeg -h long帮助的高级信息ffmpeg -h full帮助的全部信息 ffmpeg的命令使用方式:ffmpeg [options] [[infile options] -i infile] [[outfile options] outfile] 二:将帮助文档输出到文件 …...

回归预测 | Matlab实现SO-CNN-SVM蛇群算法优化卷积神经网络-支持向量机的多输入单输出回归预测
Matlab实现SO-CNN-SVM蛇群算法优化卷积神经网络-支持向量机的多输入单输出回归预测 目录 Matlab实现SO-CNN-SVM蛇群算法优化卷积神经网络-支持向量机的多输入单输出回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.SO-CNN-SVM蛇群算法优化卷积神经网络-支持向量…...
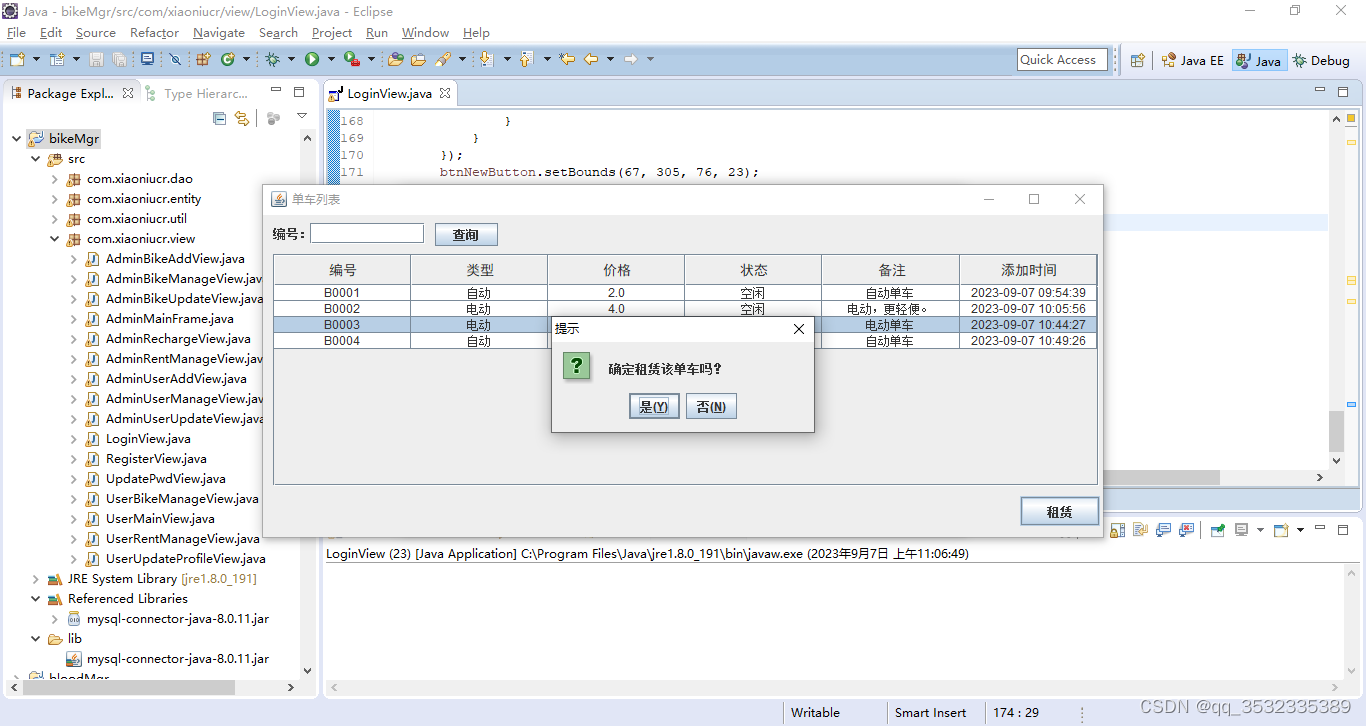
【原创】java+swing+mysql校园共享单车管理系统设计与实现
摘要: 校园共享单车作为一种绿色、便捷的出行方式,在校园内得到了广泛的应用。然而,随着单车数量的增加,管理难度也不断加大。如何提高单车的利用率和管理效率,成为校园共享单车发展面临的重要问题。本文针对这一问题…...
(自适应手机端)响应式新闻博客知识类pbootcms网站模板 自媒体运营博客网站源码下载
(自适应手机端)响应式新闻博客知识类pbootcms网站模板 自媒体运营博客网站源码下载 带后台系统PbootCMS内核开发的网站模板,该模板适用于新闻博客网站、自媒体运营网站等企业,当然其他行业也可以做,只需要把文字图片换成其他行业的即可&#…...
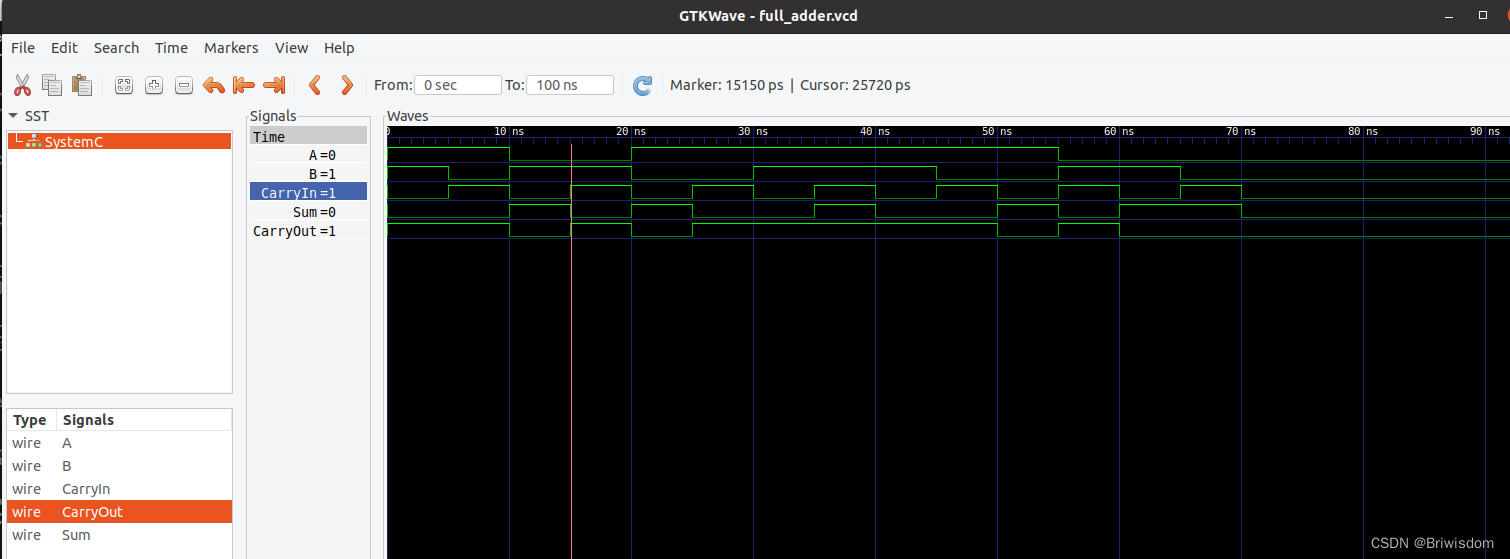
SystemC入门完整编写示例:全加器测试平台
导读: 本文将完整演示基于systemC编写一个全加器的测试平台。具体内容包括:激励平台,监控平台,待测单元的编写,波形文件读取。 1,main函数模块 搭建一个测试平台主要由:Driver, Monitor, DUT(design under …...

动手学深度学习:2.线性回归pytorch实现
动手学深度学习:2.线性回归pytorch实现 1.手动构造数据集2.小批量读取数据集3.定义模型和损失函数4.初始化模型参数5.小批量随机梯度下降优化算法6.训练完整代码Q&A 1.手动构造数据集 import torch from torch.utils import data from d2l import torch as d2l…...

重要的linux指令
系统管理命令 切换用户 su 用户名管理员身份运行 sudo 命令实时显示进程信息(linux下任务管理器) top查看进程信息(ps) ps -efps -ef | grep 进程名 ps -aux | grep 进程名参数说明e 显示所有进程f 全格式a 显示所有程序u 以用户为主的格式来显示程序状况x 显示无控制终端…...

delphi7安装并使用皮肤控件
1、下载控件 我已经上传到云盘,存储位置 2、下载后并解压。 3、打开dephi7,File-Open,打开路径D:\LC\Desktop\vclskin2_XiaZaiBa\d7, 然后将 D:\LC\Desktop\vclskin2_XiaZaiBa\d7文件夹中所有后缀.dcu的文件复制粘贴到delphi安装路…...

安徽省黄山景区免9天门票为哪般?
今日浑浑噩噩地睡了大半天,强撑起身子写网文......可是,题材不好选,本“人民体验官”只得推广人民日报官方微博文化产品《这两个月“黄山每周三免门票”》。 图:来源“人民体验官”推广平台 因年事渐高,又有未愈的呼吸…...
MFC 窗体插入图片
1.制作BMP图像1.bmp 放到res文件夹下,资源视图界面导入res文件夹下的1.bmp 2.添加控件 控件类型修改为Bitmap 图像,选择IDB_BITMAP1 3.效果...

关于中间件技术
中间件是一种独立的系统软件或服务程序,可以帮助分布式应用软件在不同的技术之间共享资源。中间件可以: 1、负责客户机与服务器之间的连接和通信,以及客户机与应用层之间的高效率通信机制。 2、提供应用的负载均衡和高可用性、安全机制与管…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
