游戏引擎中为什么要用四元数表示旋转而不用欧拉角旋转?
个人观点,仅供参考,如有错误可太刺激了
四元数的简单概念和使用
欧拉角通常用于表示一个物体的旋转状态,而不是表示旋转过程。
欧拉角描述的是物体相对于某个参考坐标系的朝向或旋转状态,通常以不同的轴(例如,绕X轴、Y轴和Z轴)的旋转角度来表示。这可以让你知道物体是如何朝向的,但它不提供旋转的完整信息。 当你用三个欧拉角表示一个旋转状态时,绕三个轴旋转的顺序不同,会得到不同的旋转结果。这些性质,就导致了以下这些问题:
欧拉角存在的问题
- 万向锁(Gimbal Lock): Gimbal Lock 是一个常见的问题,会导致旋转自由度的丢失
- 非唯一性: 欧拉角表示不是唯一的,相同的旋转可以用多种不同的欧拉角组合来表示,这很扯淡
- 不连续性: 欧拉角旋转可能会导致不连续性,特别是在插值时,会导致角度的突然跳跃,使得动画过渡不平滑
- 旋转顺序依赖: 欧拉角旋转的结果依赖于旋转轴的顺序,因此必须明确定义旋转顺序
- 数学计算复杂性: 进行欧拉角旋转计算需要需要复杂的矩阵运算
四元数的优点:
- 一个四元数通常需要存储4个分量(w、x、y、z),而旋转矩阵通常需要存储9个分量(3x3矩阵)。由于存储空间较小,四元数在内存中占用更少的空间。
- 计算效率: 四元数的乘法运算相对于矩阵乘法来说计算更快,因为四元数只涉及4个分量的乘法和加法,而矩阵涉及9个分量的乘法和加法。这在计算机图形和游戏中非常重要,因为需要频繁执行旋转操作。
- 插值: 四元数在插值(如球形线性插值)方面表现更好。插值旋转矩阵涉及到矩阵分解和插值,而四元数的插值通常更简单和高效。
- 避免万向锁: 四元数在避免万向锁问题上更稳定。欧拉角旋转和旋转矩阵都可能在特定情况下遇到万向锁问题,而四元数通常不会。
- 四元数既可以表示朝向,也能表示变换到当前朝向的旋转变换。
怎么理解优点5:也能表示变换到当前朝向的旋转变换?
案例: 一个游戏对象,在世界空间中以某个姿态摆放着,已知该物体的面朝方向的欧拉角表示为 forward = (roll, pitch, yaw),求其 Up 向量和 Right 向量
- 一般计算方法:非常简单且好理解,用叉乘
glm::vec3 forward = getObjectTransform().Rotation; // 物体的朝向 glm::vec3 worldUp = glm::vec3(0.0f, 1.0f, 0.0f); glm::vec3 RightInWorld = glm::normalize(glm::cross(worldUp, forward)); glm::vec3 UpInWorld = glm::normalize(glm::cross(forward, Right)); - 用四元数计算: 因为当前朝向的四元数同时也代表了物体的局部坐标空间中物体朝向变换到世界空间中的当前朝向的旋转变换,因此把该四元数变换应用给局部
Up和Right就能得到物体当前在世界空间中的的Up和Rightglm::quat forwardQuad = glm::quat(getObjectTransform().Rotation);glm::vec3 UpInWorld = glm::rotate(forwardQuad, glm::vec3(0.0f, 1.0f, 0.0f); glm::vec3 RightInWorld = glm::rotate(forwardQuad, glm::vec3(1.0f, 0.0f, 0.0f));
二者计算量其实差不多,根据需要选择方法即可。
相关文章:

游戏引擎中为什么要用四元数表示旋转而不用欧拉角旋转?
个人观点,仅供参考,如有错误可太刺激了 四元数的简单概念和使用 欧拉角通常用于表示一个物体的旋转状态,而不是表示旋转过程。 欧拉角描述的是物体相对于某个参考坐标系的朝向或旋转状态,通常以不同的轴(例如&#x…...
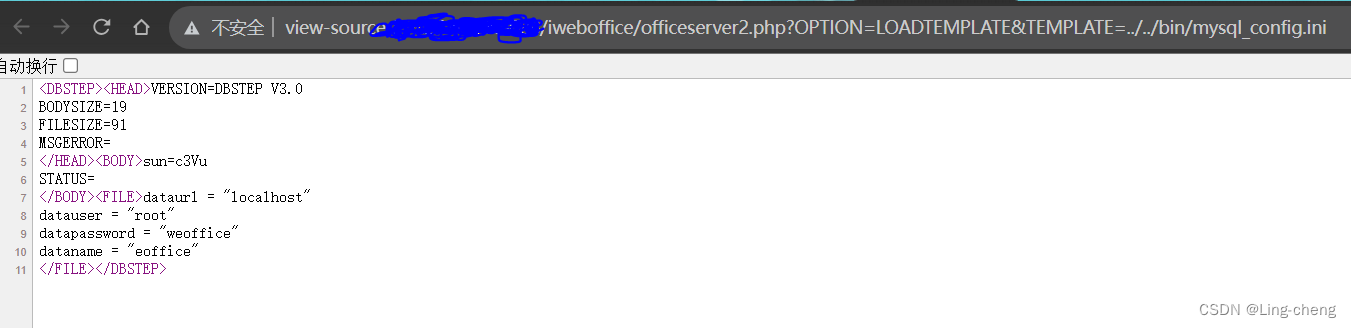
E-Office(泛微OA)前台任意文件读取漏洞复现
简介 泛微E-Office是一款企业级的全流程办公自动化软件,它包括协同办公、文档管理、知识管理、工作流管理等多个模块,涵盖了企业日常工作中的各个环节。在该产品前台登录页存在文件读取漏洞。 officeserver.php文件存在任意文件读取漏洞,通…...

前端小案例 | 喵喵大王立大功 | 一个带便利贴功能的todolist面板
文章目录 📚html📚css📚js🐇stickynote.js🐇todolist.js🐇clock.js 📚html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><m…...

算法训练营第十一天 | 20. 有效的括号、 1047. 删除字符串中的所有相邻重复项、150. 逆波兰表达式求值
目录: 力扣 20. 有效的括号力扣 1047. 删除字符串中的所有相邻重复项力扣 150. 逆波兰表达式求值 问题一、 20. 有效的括号 题目链接:20. 有效的括号 - 力扣(LeetCode) 思路分析: 很多朋友刚开始接触这一类题的时候…...
Python unittest单元测试框架 TestSuite测试套件
TestSuite 测试套件简介 对一个功能的验证往往是需要很多多测试用例,可以把测试用例集合在一起执行,这就产生了测试套件TestSuite 的概念,它是用来组装单个测试用例,规定用例的执行的顺序,而且TestSuite也可以嵌套Tes…...

FSB逮捕为乌克兰网络部队工作的俄罗斯黑客
导语 近日,俄罗斯联邦安全局(FSB)逮捕了两名涉嫌协助乌克兰网络部队对俄罗斯重要基础设施目标进行网络攻击的个人。这起事件引起了广泛关注,涉及到了网络安全和国际关系等多个领域。本文将为您详细介绍这一事件的背景和最新进展。…...
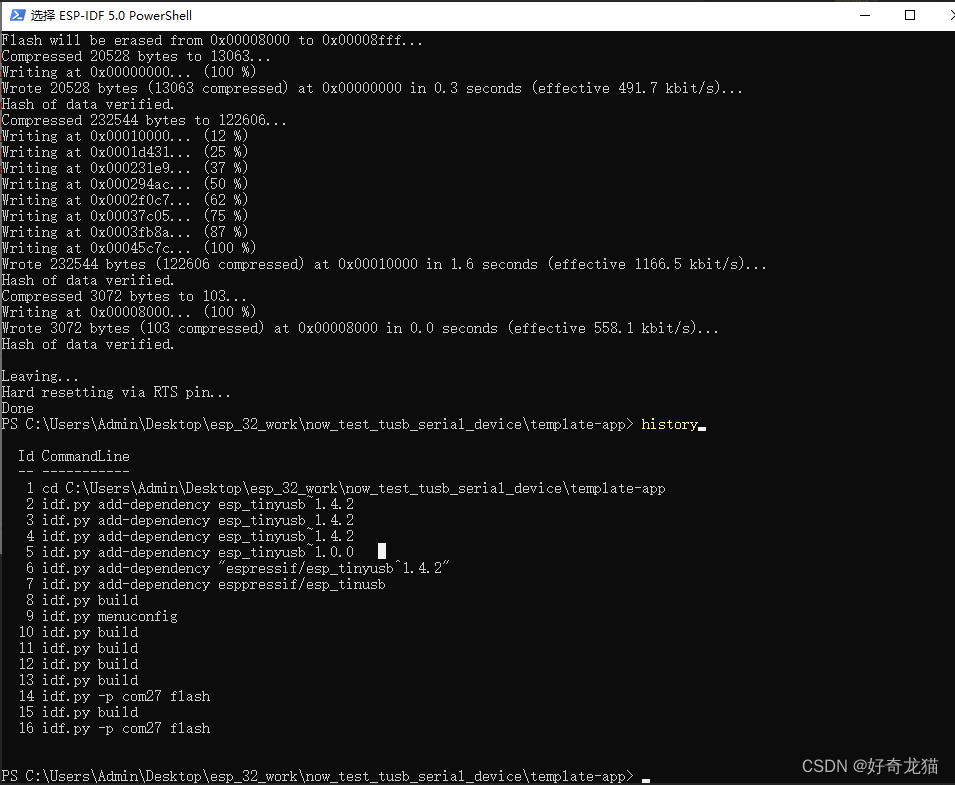
【PC电脑windows-学习样例tusb_serial_device-ESP32的USB模拟串口程序+VScode建立工程+usb组件添加+-基础样例学习】
【PC电脑windows-学习样例tusb_serial_device-ESP32的USB模拟串口程序-基础样例学习】 1、概述2、实验环境3-1、 物品说明3-2、所遇问题:ESP32 cannot open source file "tinyusb.h"或者“tinyusb.h:No such file or directory ....”3-3、解决问题&#…...

LeetCode75——Day26
文章目录 一、题目二、题解 一、题目 394. Decode String Given an encoded string, return its decoded string. The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guar…...
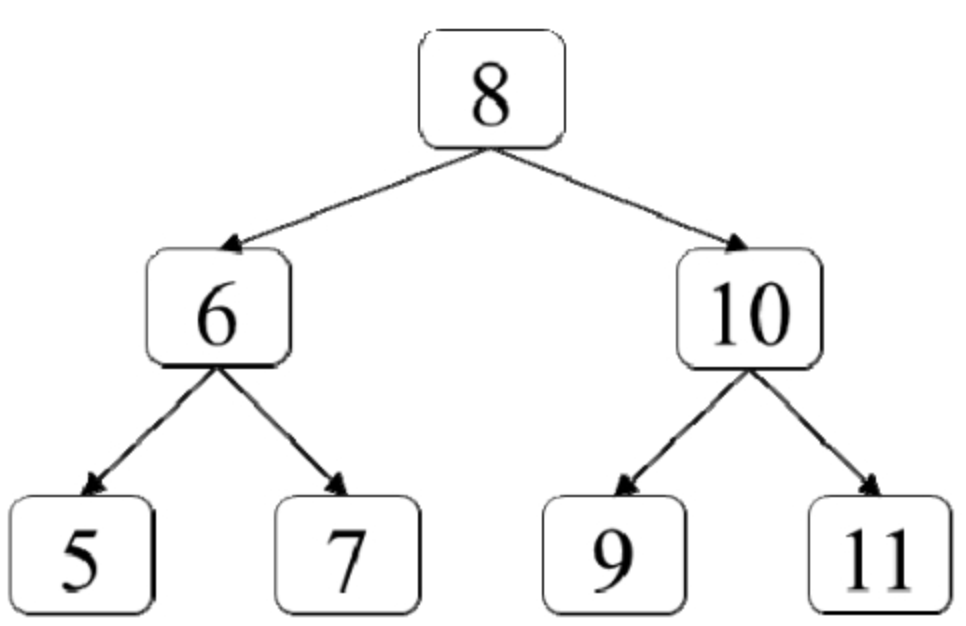
面试算法53:二叉搜索树的下一个节点
题目 给定一棵二叉搜索树和它的一个节点p,请找出按中序遍历的顺序该节点p的下一个节点。假设二叉搜索树中节点的值都是唯一的。例如,在图8.9的二叉搜索树中,节点8的下一个节点是节点9,节点11的下一个节点是null。 分析…...

2023SHCTF web方向wp
1.ezphp 看一眼,你大爷,啥玩意都给我过滤完了。 还好下面有preg_replace()/e,会把replacement当作php语句执行 传参pattern.*, .*表示任意字符,code{${phpinfo()}} ,为什么这样写,因为,print_…...
从物理磁盘到数据库 —— 存储IO链路访问图
原图来自:数据库IO链路访问图 – OracleBlog 由于很复杂,为了加深理解自己重新画了一次,另外参考其他文档补充了各部分的插图和介绍。 一、 存储服务器 1. 物理磁盘 外层的壳子称为硬盘笼 cage 2. chunklet Chunklet 是一个虚拟概念而不是实…...
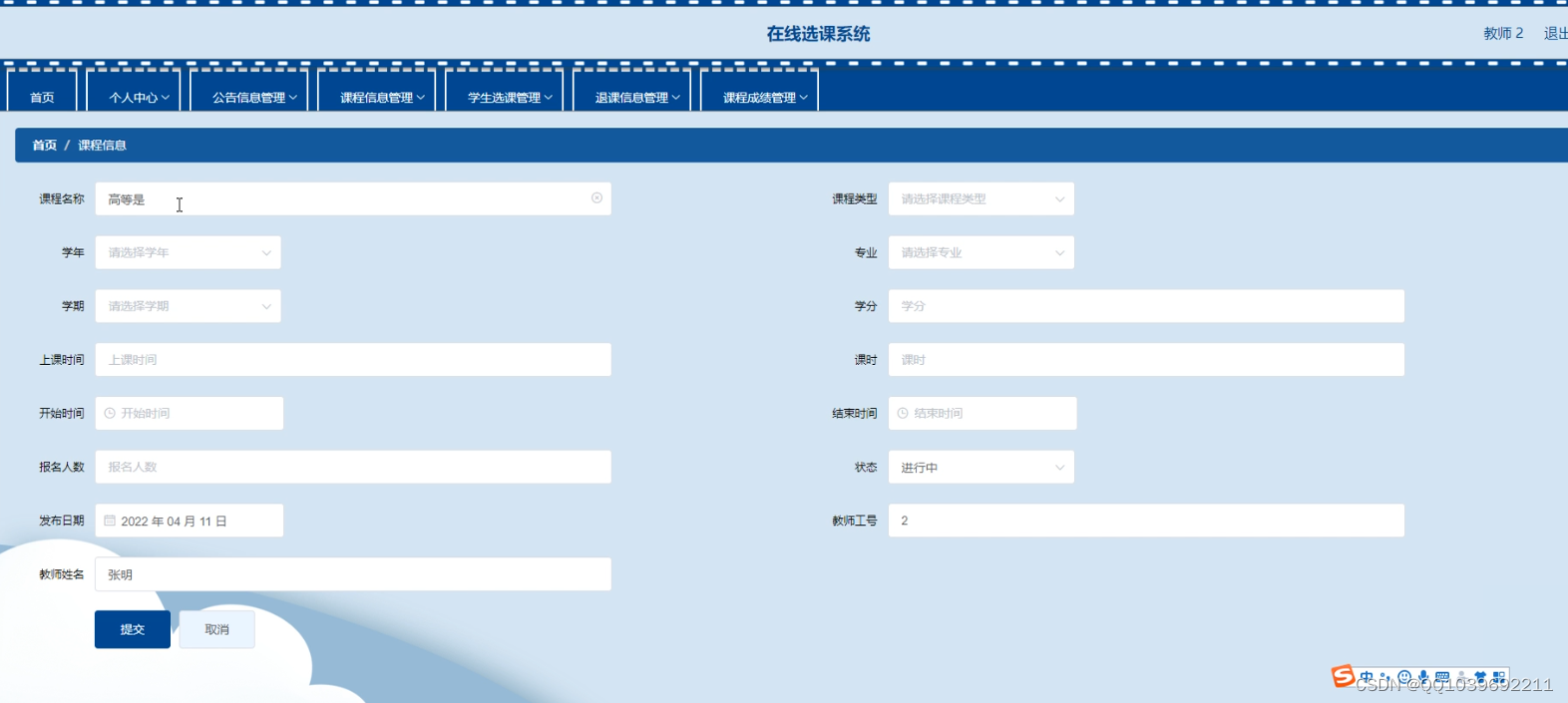
基于java+springboot+vue在线选课系统
项目介绍 本系统结合计算机系统的结构、概念、模型、原理、方法,在计算机各种优势的情况下,采用JAVA语言,结合SpringBoot框架与Vue框架以及MYSQL数据库设计并实现的。员工管理系统主要包括个人中心、课程管理、专业管理、院系信息管理、学生…...

GO学习之 同步操作sync包
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 10、GO学习之 网络通信(Net/Htt…...
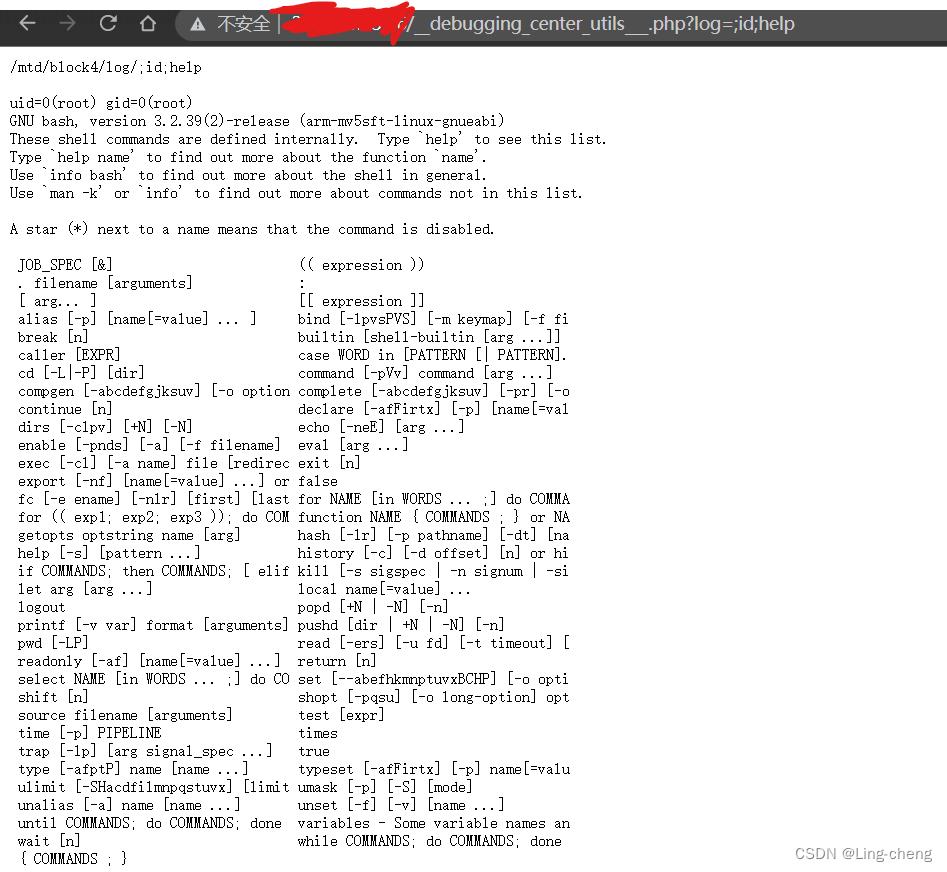
NUUO网络摄像头(NVR)RCE漏洞复现
简介 NUUO Network Video Recorder(NVR)是中国台湾NUUO公司的一款网络视频记录器。 NUUO NVR视频存储管理设备的__debugging_center_utils___.php文件存在未授权远程命令执行漏洞,攻击者可在没有任何权限的情况下通过log参数执行任意命令。…...

一款快速获取目标网站关键信息的工具
1.摘要 今天要介绍的这款工具是一个快速收集网站信息的开源脚本, 采用Python语言编写, 该工具可以快速收集网站的页面标题、网站上次更新日期、DNS信息、子域、防火墙名称、网站使用的技术栈、证书等信息, 默认支持对验证码和JavaScript内容执行绕过操作。 2.工具安装使用 使…...

将GC编程语言引入WebAssembly的新方法
本文讨论了一种名为 WasmGC 的新方法,用于将垃圾收集编程语言有效地引入 WebAssembly。 WasmGC 定义了新的 GC 类型,例如结构和数组,与之前编译为线性内存的方法 (WasmMVP) 相比,它们可以实现更好的优化: 在编译时和…...

微信小程序UI自动化测试实践:Minium+PageObject
小程序架构上分为渲染层和逻辑层,尽管各平台的运行环境十分相似,但是还是有些许的区别(如下图),比如说JavaScript 语法和 API 支持不一致,WXSS 渲染表现也有不同,所以不论是手工测试,…...

Java零基础入门-输入与输出
哈喽,各位小伙伴们,你们好呀,我是喵手。 今天我要给大家分享一些自己日常学习到的一些知识点,并以文字的形式跟大家一起交流,互相学习,一个人虽可以走的更快,但一群人可以走的更远。 我是一名后…...

iOS报错命名空间“std”中的“unary_function”
刚刚将我的 Xcode 升级到 15.0,突然它开始在 RCT_Folly 中出现以下错误 No template named unary_function in namespace std; did you mean __unary_function?我尝试删除缓存数据和派生数据并清理构建。也尝试删除 pod 和 node_modules。但没有任何帮助。 于是我…...
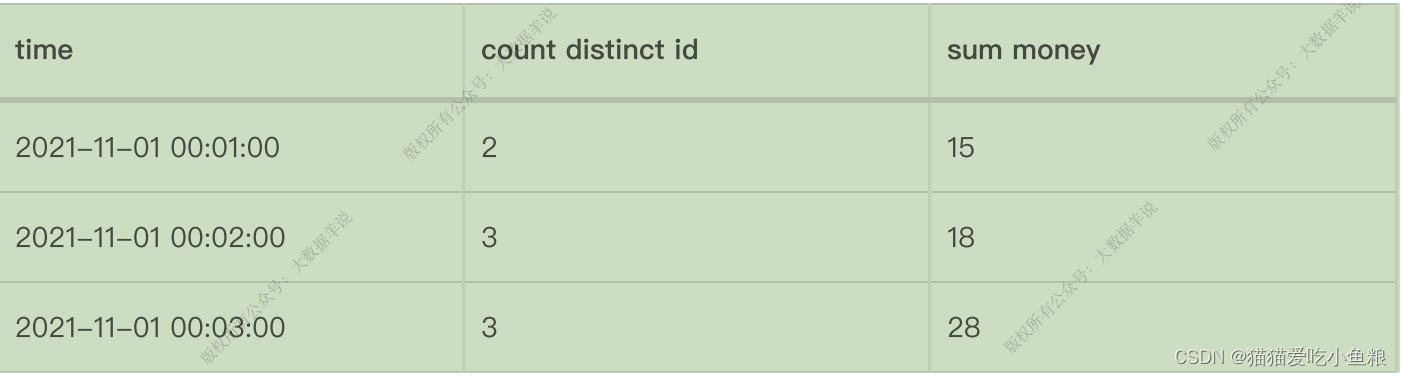
Flink SQL 窗口聚合详解
1.滚动窗⼝(TUMBLE) **滚动窗⼝定义:**滚动窗⼝将每个元素指定给指定窗⼝⼤⼩的窗⼝,滚动窗⼝具有固定⼤⼩,且不重叠。 例如,指定⼀个⼤⼩为 5 分钟的滚动窗⼝,Flink 将每隔 5 分钟开启⼀个新…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
