【数据结构】数组和字符串(十五):字符串匹配2:KMP算法(Knuth-Morris-Pratt)
文章目录
- 4.3 字符串
- 4.3.1 字符串的定义与存储
- 4.3.2 字符串的基本操作
- 4.3.3 模式匹配算法
- 0. 朴素模式匹配算法
- 1. ADL语言
- 2. KMP算法分析
- 3. 手动求失败函数
- 定义
- 例1
- 例2
- 例3
- 4. 自动求失败函数(C语言)
- 5. KMP算法(C语言)
- 6. 失败函数答案
- 例2
- 例3
4.3 字符串
字符串(String)是由零个或多个字符(char)顺序排列组成的有限序列,简称为串。例如 “good morning”就是由12个字符构成的一个字符串。一般把字符串记作:
S = ′ ′ a 0 a 1 … a n − 1 ′ ′ S=''a_{0} a_{1}…a_{n-1}'' S=′′a0a1…an−1′′
其中S是串名,引号中的字符序列是串值。字符个数是串的长度,长度为0的串被称为空串,因为它不包含任何字符。需要注意的是,空格字符(" ")并不是空串,因为它包含一个字符——空格。
若把某个串称为主串,则主串中任意个连续的字符组成的子序列被称为子串。子串在主串中第一次出现时,其首字符在主串中的序号被称为该子串在主串中的位置。
关于字符串的基础知识亦可参考前文:
【重拾C语言】六、批量数据组织(三)数组初值;字符串、字符数组、字符串数组;类型定义 typedef
【重拾C语言】七、指针(三)指针与字符串(字符串与字符串数组;指针与字符串的遍历、拷贝、比较;反转字符串)
4.3.1 字符串的定义与存储
字符串在许多非数值计算问题中扮演着重要的角色,并在模式匹配、程序编译和数据处理等领域得到广泛应用。在高级程序设计语言中,字符串通常被定义为以特殊字符’\0’(称为空字符或字符串结束符)结尾的字符序列。这个约定使得在处理字符串时可以方便地确定字符串的结束位置。关于字符串的存储方式,主要有两种常见的方式:
-
顺序存储:字符串的字符按照顺序依次存储在连续的内存空间中。这种方式使得字符串的访问和操作效率较高,可以通过索引直接访问任意位置的字符。在顺序存储方式中,字符串的长度可以通过计算字符个数或者遇到’\0’结束符来确定。
-
链式存储:字符串的字符通过链表的方式进行存储。每个节点包含一个字符和指向下一个节点的指针。链式存储方式可以动态地分配内存,适用于长度可变的字符串。但是相比于顺序存储,链式存储方式需要更多的内存空间,并且访问字符需要遍历链表。
选择何种存储方式取决于具体的应用场景和需求。顺序存储适合于需要频繁访问和操作字符串的情况,而链式存储适合于长度可变的字符串或者对内存空间要求较高的情况。具体C语言实现可参照前文:
【数据结构】数组和字符串(十一):字符串的定义与存储(顺序存储、链式存储及其C语言实现)
4.3.2 字符串的基本操作
顺序存储:【数据结构】数组和字符串(十二):顺序存储字符串的基本操作(串长统计、查找、复制、插入、删除、串拼接)
链式存储:【数据结构】数组和字符串(十三):链式字符串的基本操作(串长统计、查找、复制、插入、删除、串拼接)
4.3.3 模式匹配算法
文本编辑器中常用的“查找”、“替换”和“全部替换”等基本的编辑操作就是最普通的模式匹配问题,即:在文本文件中查找串。它的查找过程可简单描述如下:给定两个字符串变量 S 和 P,其中目标串 S 有n个字符,模式串P有m个字符,m≤n . 从S的给定位置(通常为S的第一个字符)开始,搜索模式串P,如果找到,返回模式串P在S中匹配成功的起始位置;如果没找到(即S中没有P),则返回–1 .
字符串匹配可以采用多种算法,包括朴素模式匹配算法、KMP(Knuth-Morris-Pratt)算法、Boyer-Moore算法等。这些算法的性能和效率各不相同,具体选择取决于应用的需求和文本数据的规模。
0. 朴素模式匹配算法
- 朴素模式匹配算法:【数据结构】数组和字符串(十四):字符串匹配1:朴素的模式匹配算法(StringMatching)
朴素模式匹配算法的优点是过程简单,缺点是效率低。在最坏情况下,该算法要匹配n-m+1次,每次匹配要做m次比较。本文将介绍更高效的模式匹配算法——KMP算法
1. ADL语言

2. KMP算法分析
待完善
3. 手动求失败函数
定义
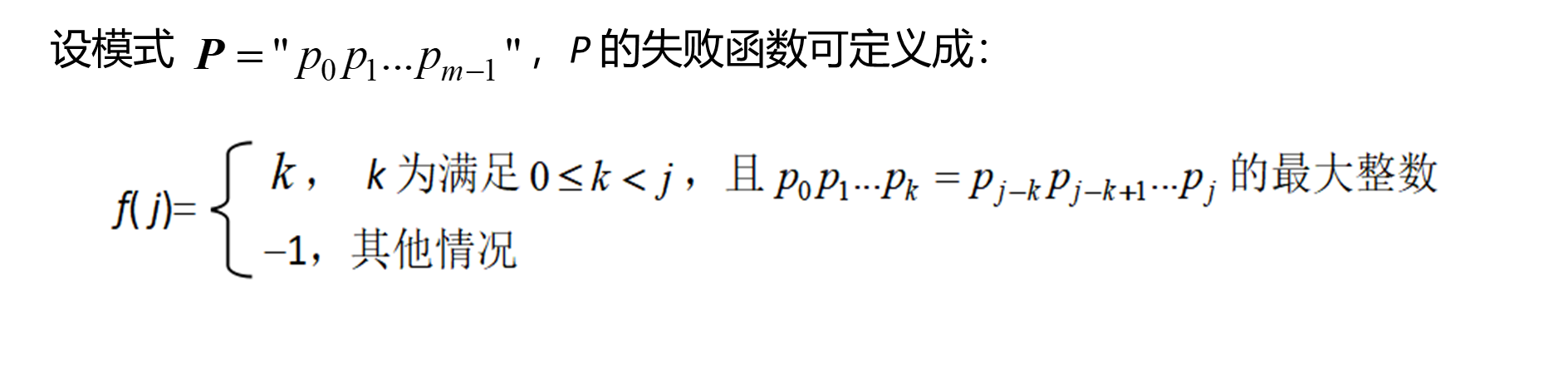
例1
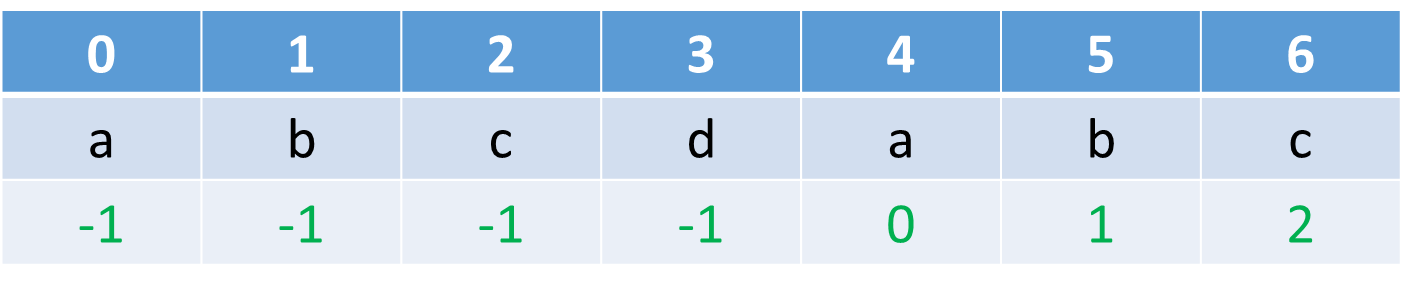
例2
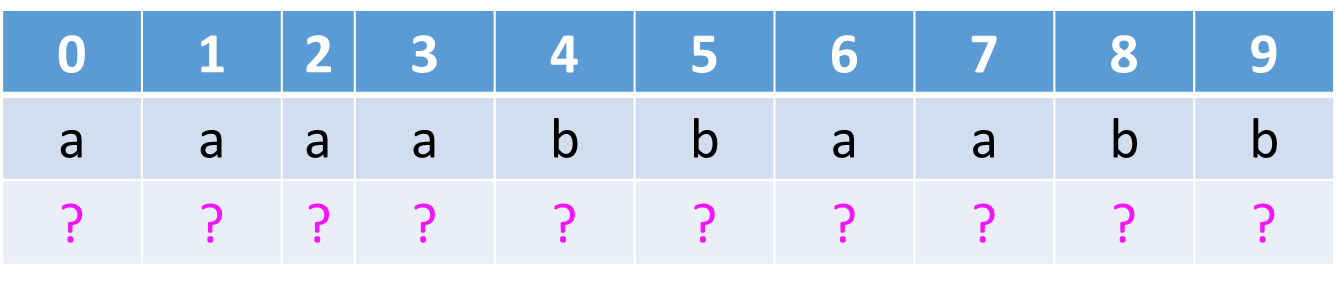
例3

答案见文末
4. 自动求失败函数(C语言)

#include <stdio.h>
#include <string.h>void buildFailureFunction(const char* P, int m, int* F) {int i = 1, j = 0;F[0] = -1;while (i < m) {if (P[i] == P[j]) {j++;F[i] = j - 1;i++;} else {if (j != 0) {j = F[j - 1];} else {F[i] = -1;i++;}}}
}int main() {
// const char* P = "abcdabc";
// const char* P = "aaaabbaabb";const char* P = "abcabcabcabcabcabc";int m = strlen(P);int F[m];buildFailureFunction(P, m, F);printf("模式串P: %s\n", P);printf("失败函数F(P): ");for (int i = 0; i < m; i++) {printf("%d ", F[i]);}printf("\n");return 0;
}
5. KMP算法(C语言)
#include <stdio.h>
#include <string.h>void buildFailureFunction(const char* P, int m, int* F) {int i = 1, j = 0;F[0] = 0;while (i < m) {if (P[i] == P[j]) {j++;F[i] = j;i++;} else {if (j != 0) {j = F[j - 1];} else {F[i] = 0;i++;}}}
}int kmpPatternMatching(const char* S, const char* P, int* comparisons) {int n = strlen(S); // 目标串的长度int m = strlen(P); // 模式串的长度int position = -1; // 初始化位置为-1int F[m]; // 失败函数表buildFailureFunction(P, m, F);int i = 0, j = 0;while (i < n) {(*comparisons)++; // 比较次数加1if (S[i] == P[j]) {i++;j++;if (j == m) { // 如果模式串完全匹配position = i - m;break;}} else {if (j != 0) {j = F[j - 1];} else {i++;}}}return position;
}int naivePatternMatching(const char* S, const char* P, int* comparisons) {int n = strlen(S); // 目标串的长度int m = strlen(P); // 模式串的长度int position = -1; // 初始化位置为-1for (int i = 0; i <= n - m; i++) {int j = 0;while (j < m && S[i + j] == P[j]) {(*comparisons)++; // 比较次数加1j++;}if (j == m) { // 如果模式串完全匹配position = i; // 设置匹配位置break;}}return position;
}int main() {const char* S = "abcabcabcabcabcabd";const char* P = "abcabd";int comparisons = 0; // 比较次数初始化为0int result1 = naivePatternMatching(S, P, &comparisons);if (result1 != -1) {printf("朴素模式匹配算法:模式串在目标串中的位置: %d\n", result1);} else {printf("未找到匹配\n");}printf("朴素模式匹配算法:比较次数: %d\n", comparisons);comparisons = 0; // 比较次数初始化为0int result2 = kmpPatternMatching(S, P, &comparisons);if (result2 != -1) {printf("KMP算法:模式串在目标串中的位置: %d\n", result2);} else {printf("未找到匹配\n");}printf("KMP算法:比较次数: %d\n", comparisons);return 0;
}

6. 失败函数答案
例2
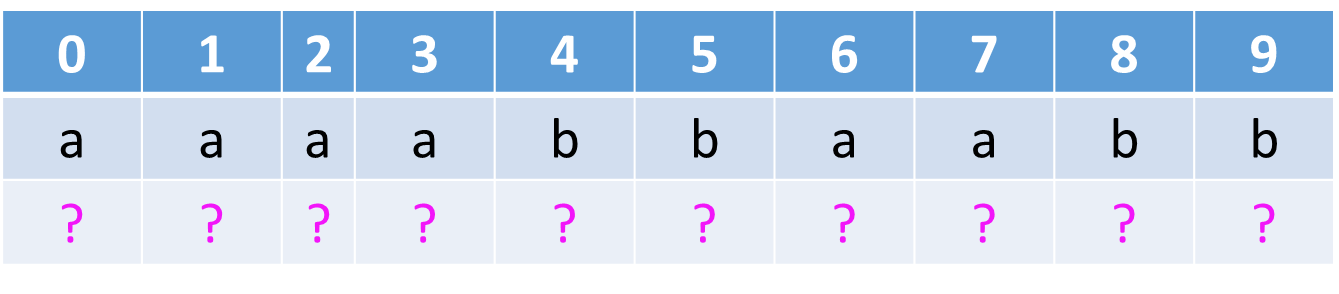

例3


相关文章:

【数据结构】数组和字符串(十五):字符串匹配2:KMP算法(Knuth-Morris-Pratt)
文章目录 4.3 字符串4.3.1 字符串的定义与存储4.3.2 字符串的基本操作4.3.3 模式匹配算法0. 朴素模式匹配算法1. ADL语言2. KMP算法分析3. 手动求失败函数定义例1例2例3 4. 自动求失败函数(C语言)5. KMP算法(C语言)6. 失败函数答案…...

STM32 PWM可控制电压原理
PWM可控制电压原理 主要通过PWM 输入模式根据控制单位时间内输出的平均电压,以调节电压大小。而PWM输出模式通过调节占空比,控制平均电压大小; 设置TIM为PWM输出模式 第一步:时钟使能: GPIO,TIM; 第二步&a…...

angular、 react、vue框架对比
借鉴:Web前端开发:三大主流框架 (baidu.com) AngularReactVue公司ChromeFaceBook尤雨溪写法有指令、模板的概念比较灵活,没有要求使用特定的架构和模式有指令和模板的概念性能低有虚拟Dom,性能高有虚拟Dome,性能高学习门槛 高&am…...

GNSS常用数据源汇总
本文整理汇总了GNSS数据处理过程中常用的数据源,路径中的占位符具体含义如下: -YYYY-年-YY-年的后两位数-DOY-年积日-MM-月-HH-小时-WWWW-GPS周 一、RINEXO观测值与RINEXN星历小时文件 1、CDDIS:ftp://gdc.cddis.eosdis.nasa.gov/pub/gnss…...
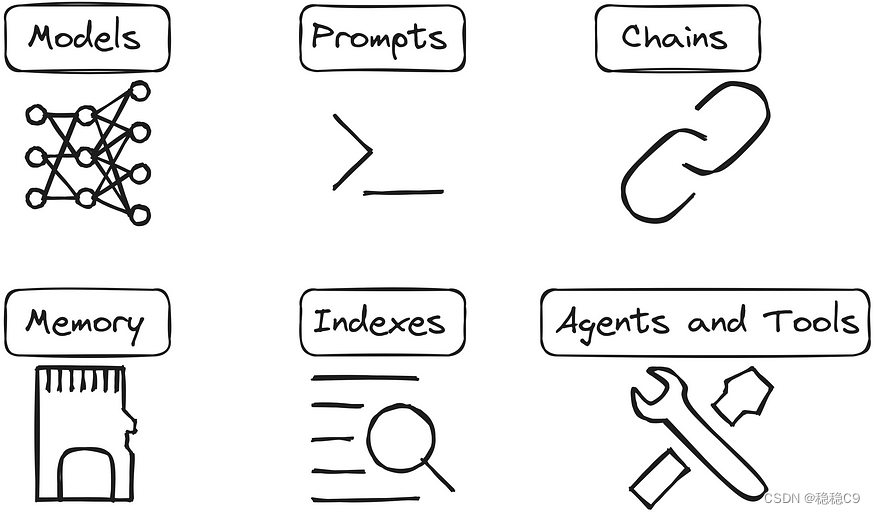
01|LangChain | 从入门到实战-介绍
by:wenwenc9 一、基本知识储备 1、什么是大模型,LLM? 大模型(Large Language Model)是近年来一个很热门的研究方向。 使用大量的数据训练出一个非常大的模型。一般是数十亿到上万亿的参数规模。 这些大模型可以捕捉到非常复杂的语言…...
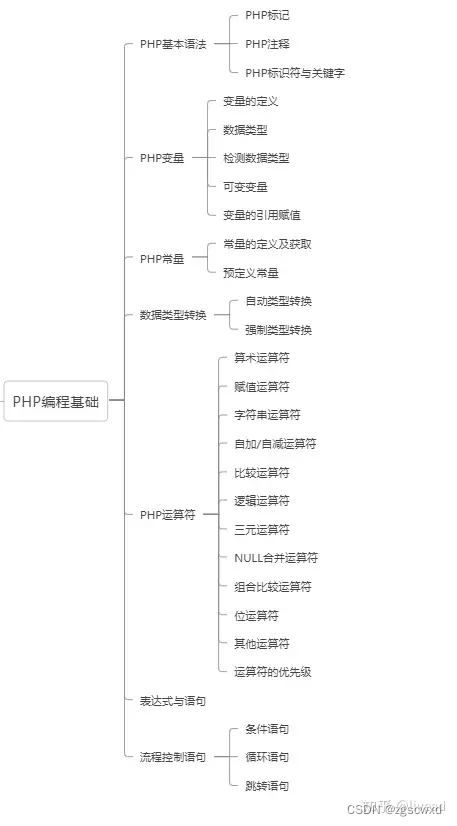
【小白专用】PHP基本语法 23.11.04
PHP基本语法 PHP是超文本预处理器 由服务器解析执行 可以与 html 进行混编(嵌入) ,PHP是一种弱类型语言 1.1 PHP标记 PHP和其他Web语言一样,都是用一对标记将PHP代码包含起来,以便和HTML代码区分开来。PHP支持4种风格的标记,如表所示。 标…...
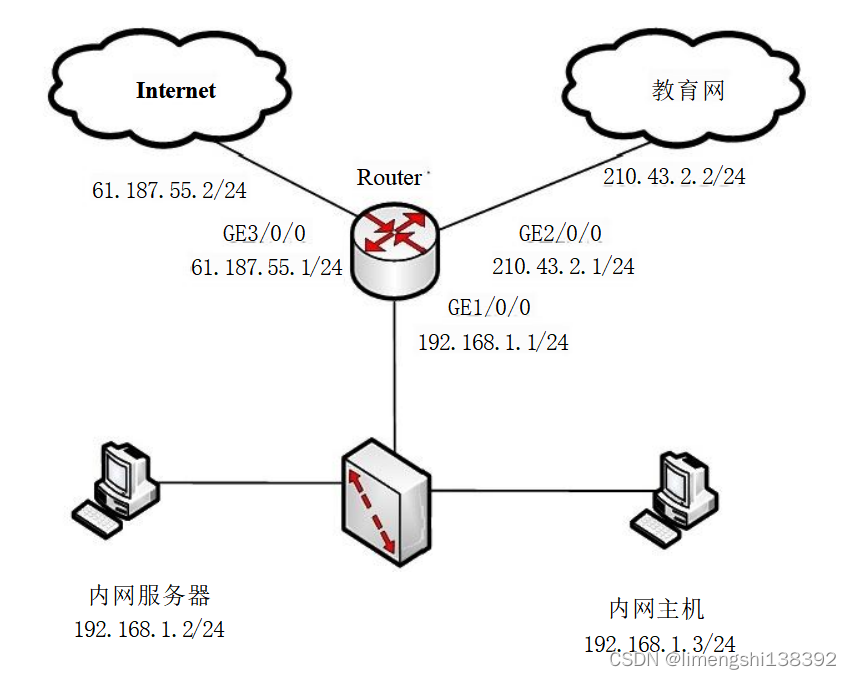
路由器基础(七):NAT原理与配置
一、NAT 配置 华为路由器配置NAT 的方式有很多种,考试中可能考到的基本配置方 式主要有EasyIP和通过NAT地址池的方式。图22-7-1是一个典型的通过EasyIP进行NAT的示意图,其中Router出接口GE0/0/1的IP地址为200.100.1.2/24,接口E0/0/1的IP地址为192.168.0.…...

Spring Boot 整合SpringSecurity和JWT和Redis实现统一鉴权认证
📑前言 本文主要讲了Spring Security文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 🌄每日一句:努力…...
交换机基础(零):交换机基础配置
一、华为设备视图 常用视图 名称 进入视图 视图功能 用户视图 用户从终端成功登录至设备即进 入用户视图,在屏幕上显示 kHuawei> 用户可以完成查看运行状态和统 计信息等功能。在其他视图下 都可使用return直接返回用户视 图 系统视图 在用户视图下&…...

02 线性组合、张成的空间与基
线性组合、张成的空间与基 基向量缩放向量并相加给定向量张成的空间线性相关与线性无关空间的基 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 基向量 当看到一对描述向量的数时,比如[3,-2]时,把这对数中的每个数(坐标&…...
解析mfc100u.dll文件丢失的修复方法,快速解决mfc100u.dll问题
在计算机使用过程中,我们经常会遇到一些错误提示,其中最常见的就是“缺少某个文件”的错误。最近,我也遇到了一个这样的问题,那就是“mfc100u.dll丢失”。这个问题可能会导致某些应用程序无法正常运行,给我们带来困扰。…...
免费外文文献检索网站,你一定要知道
01. Sci-Hub 网址链接:https://tool.yovisun.com/scihub/ Sci-hub是一个可以无限搜索、查阅和下载大量优质论文的数据库。其优点在于可以免费下载论文文献。 使用方法: 在Sci—hub搜索栏中粘贴所需文献的网址或者DOI,然后点击右侧的open即可…...

大数据毕业设计选题推荐-收视点播数据分析-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...
传智杯-21算法赛初赛B组题目详细解法解析-AB题(C/C++、Python、Java)
🚀 欢迎来到 ACM 算法题库专栏 🚀 在ACM算法题库专栏,热情推崇算法之美,精心整理了各类比赛题目的详细解法,包括但不限于ICPC、CCPC、蓝桥杯、LeetCode周赛、传智杯等等。无论您是刚刚踏入算法领域,还是经验丰富的竞赛选手,这里都是提升技能和知识的理想之地。 ✨ 经典…...

post给后端传递数组和多个参数
这是前端的数据结构 data() {return {loading: false,inputForm: {id: ${gridProject.id},gridName: ,gridId: ,projectName: ,projectId: ,type: },data: [],value: []}}, 其中 gridId 和 type 是单个参数 , value 是个数组,注意 这里data中的value[]不要直接给后…...
音频修复增强软件iZotope RX 10 mac中文特点
iZotope RX 10 mac是一款音频修复和增强软件。 iZotope RX 10 mac主要特点 声音修复:iZotope RX 10可以去除不良噪音、杂音、吱吱声等,使音频变得更加清晰干净。 音频增强:iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限制器等处…...

【面试】虚拟机栈面试题
目录 一、举例栈溢出的情况二、调整栈大小,能保证不出现溢出吗?三、分配的栈内存越大越好吗?四、垃圾回收是否会涉及到虚拟机栈?五、方法中定义的局部变量是否存在线程安全问题?5.1 说明5.2 代码示例 一、举例栈溢出的…...

白话熵增定律
白话熵增定律 热力学中的熵增定律 熵是指一个系统的混乱程度的度量,是热力学中的一个系统的属性。熵增定律是指一个封闭的系统随着时间的发展,在朝平衡状态发展时,其熵会增加,即其越来越混乱。 对于一个房间,如果经常…...
End-to-end people detection in crowded scenes)
(论文阅读14/100)End-to-end people detection in crowded scenes
文献阅读笔记 简介 题目 End-to-end people detection in crowded scenes 作者 Russell Stewart, Mykhaylo Andriluka 原文链接 https://arxiv.org/pdf/1506.04878.pdf 关键词 Null 研究问题 当前的人员检测器要么以滑动窗口的方式扫描图像,要么对一组离…...

Go的错误处理
什么是错误? 错误表示程序中发生的任何异常情况。假设我们正在尝试打开一个文件,但该文件在文件系统中不存在。这是一种异常情况,表示为错误。 Go 中的错误是普通的旧值。就像任何其他内置类型(例如 int、float64 等)…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
