插值表达式 {{}}
前言
持续学习总结输出中，今天分享的是插值表达式 {{}}
Vue插值表达式是一种Vue的模板语法，我们可以在模板中动态地用插值表达式渲染出Vue提供的数据绑定到视图中。插值表达式使用双大括号{{ }}将表达式包裹起来。
1.作用：
利用表达式进行插值，渲染到页面中
表达式：是可以被求值的代码，JS引擎会讲其计算出一个结果
如：以下的情况都是表达式
money + 100
money - 100
money * 10
money / 10
price >= 100 ? '真贵':'还行'
obj.name
arr[0]
fn()
obj.fn()
2.语法
插值表达式语法：{{ 表达式 }}
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta http-equiv="X-UA-Compatible" content="IE=edge"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>插值表达式</title>
</head>
<body>
<div id="app"><p>{{ nickname }}</p><p>{{ nickname.toUpperCase() }}</p><p>{{ nickname + '你好' }}</p><p>{{ age >= 18 ? '成年' : '未成年' }}</p><p>{{ friend.name }}</p><p>{{ friend.desc }}</p>
</div><script src="https://cdn.jsdelivr.net/npm/vue@2.7.14/dist/vue.js"></script>
<script>const app = new Vue({el: '#app',data: {nickname: 'tony',age: 18,friend: {name: 'jepson',desc: '热爱学习 Vue'}}})
</script>
</body>
</html>
运行结果：
3.错误用法
1.在插值表达式中使用的数据 必须在data中进行了提供
<p>{{hobby}}</p> //如果在data中不存在 则会报错2.支持的是表达式，而非语句，比如：if for ...
<p>{{if}}</p>3.不能在标签属性中使用 {{ }} 插值 (插值表达式只能标签中间使用)
<p title="{{username}}">我是P标签</p>
4.总结
- 插值表达式的作用是什么?
利用表达式进行插值，将数据渲染页面中 - 语法格式?
{{ 表达式 }} - 插值表达式的注意点:
1、使用的数据要存在 (data)
2、支持的是表达式，而非语句 if … for
3、不能在标签属性里面使用
最后分享一句话：
生活的最好状态是冷冷清清的风风火火。
——木心
本次的分享就到这里了！！！
相关文章：
插值表达式 {{}}
前言 持续学习总结输出中，今天分享的是插值表达式 {{}} Vue插值表达式是一种Vue的模板语法，我们可以在模板中动态地用插值表达式渲染出Vue提供的数据绑定到视图中。插值表达式使用双大括号{{ }}将表达式包裹起来。 1.作用： 利用表达式进行…...
白雪公主
前言 #define 皇后 王后 在很久很久以前，有一个国王，由于王后难产致死，导致生下的孩子没母,由于缺爱，变的非常的刻薄 由于公主过于刻薄，以至于见到她的人都面色煞白感到空中飘雪 37C 的嘴怎能说出如此刻薄的话语。为了…...
宏观角度认识递归之合并两个有序链表
21. 合并两个有序链表 - 力扣（LeetCode） 依旧是利用宏观角度来看待问题，其中最主要的就是要找到重复的子问题； 题目中要求把两个有序链表进行合并，同时不能够创建新的节点，并返回链表的起始点：因…...
Leetcode-509 斐波那契数列
使用循环 class Solution {public int fib(int n) {if(n 0){return 0;}if(n 1){return 1;}int res 0;int pre1 1;int pre2 0;for(int i 2; i < n; i){res pre1 pre2;pre2 pre1;pre1 res;}return res;} }使用HashMap class Solution {private Map<Integer,Int…...
解密 docker 容器内 DNS 解析原理
背景 这几天在使用 docker 中，碰到了在容器中 DNS 解析的一些问题。故花些时间弄清了原理，写此文章分享。 1. docker run 命令启动的容器 以启动一个 busybox 容器为例： rootubuntu20:~# docker run -itd --name u1 busybox 63b59ca8aeac…...
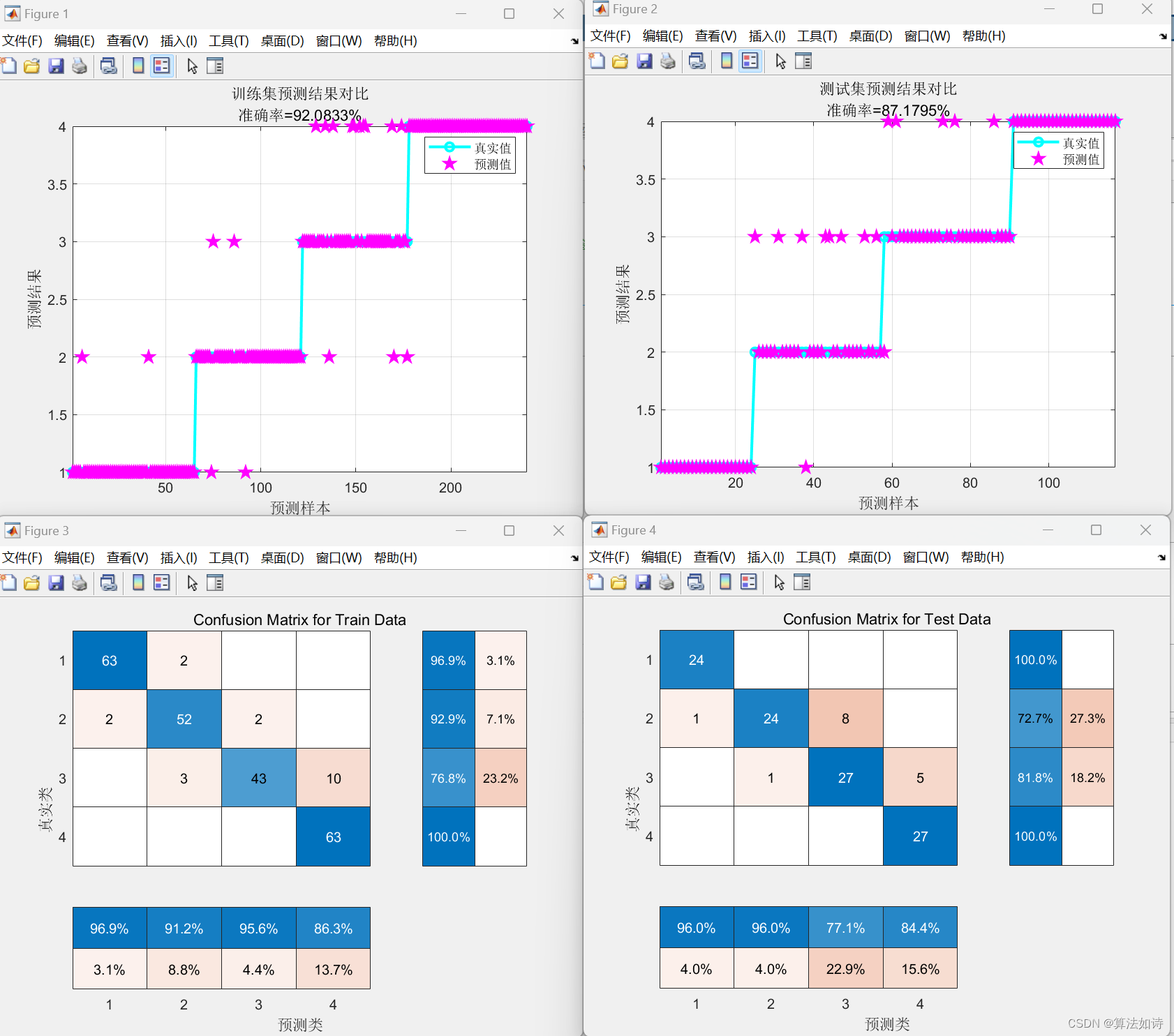
故障诊断模型 | Maltab实现SVM支持向量机的故障诊断
效果一览 文章概述 故障诊断模型 | Maltab实现SVM支持向量机的故障诊断 模型描述 Chinese: Options：可用的选项即表示的涵义如下 -s svm类型：SVM设置类型(默认0) 0 – C-SVC 1 --v-SVC 2 – 一类SVM 3 – e -SVR 4 – v-SVR -t 核函数类型：核函…...
开源的网站数据分析统计平台——Matomo
Matomo 文章目录 Matomo前言一、环境准备1. 整体安装流程2.安装PHP 7.3.303.nginx配置4.安装matomo4.1 访问安装页面 http://192.168.10.45:8088/index.php4.2 连接数据库4.3 设置管理员账号4.4 生成js跟踪代码4.5 安装完成4.6 警告修改4.7 刷新页面，就可以看到登陆…...
linux入门到地狱
linux—001入门 IT圈必备(前端工作者用的比较少) 老旧电脑跑linux不容易卡 我代码没保存windows闪退，僵停(vs2019卡掉线)，重启更新,占用cpu内存服务报错pip各种bug 出来生态环境友好其他的全是bug(bug时间成本超过了windows快捷友好生态) 那就说明wind…...
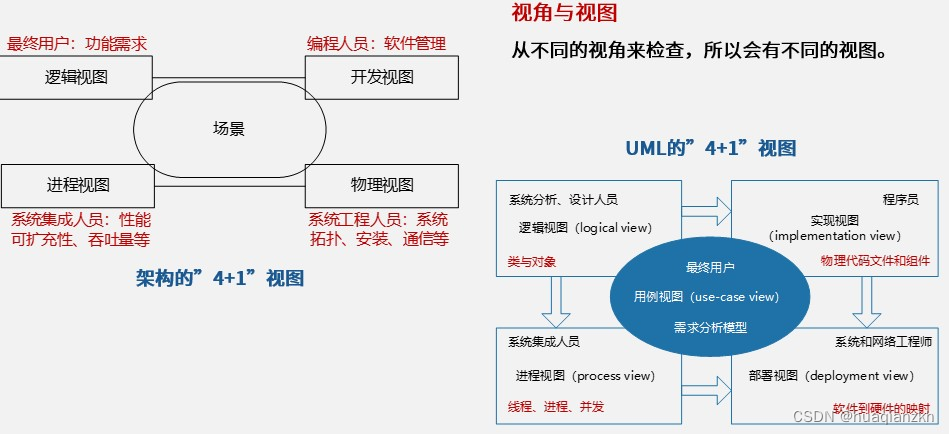
架构”4+1“视图
1995年Kruchten提出了著名的“41”视图，用来描述软件系统的架构。在“41”视图中，（物理视图 ）用来描述系统软硬件之间的映射关系，这个视图往往（系统工程人员）最为关注；（逻…...
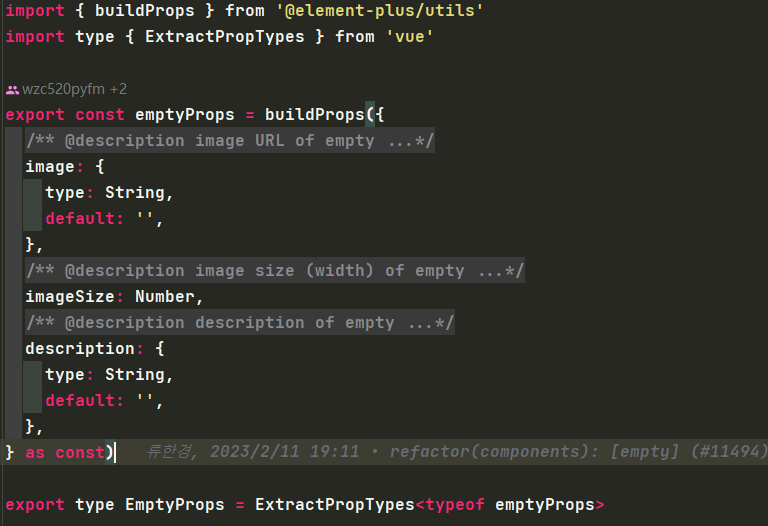
『精』Vue 组件如何模块化抽离Props
『精』Vue 组件如何模块化抽离Props 文章目录 『精』Vue 组件如何模块化抽离Props一、为什么要抽离Props二、选项式API方式抽离三、组合式API方式抽离3.1 TypeScript类型方式3.2 文件分离方式3.3 对文件分离方式优化 参考资料💘推荐博文🍗 一、为什么要抽…...
JavaScript字符串字面量详细解析与代码实例
JavaScript字符串字面量是一种表示字符串值的语法结构，通常用双引号或单引号括起来。 var str1 "Hello World!"; var str2 Hello World!;另外，如果需要在字符串中包含双引号或单引号，可以使用转义字符\来实现。 var str3 &quo…...
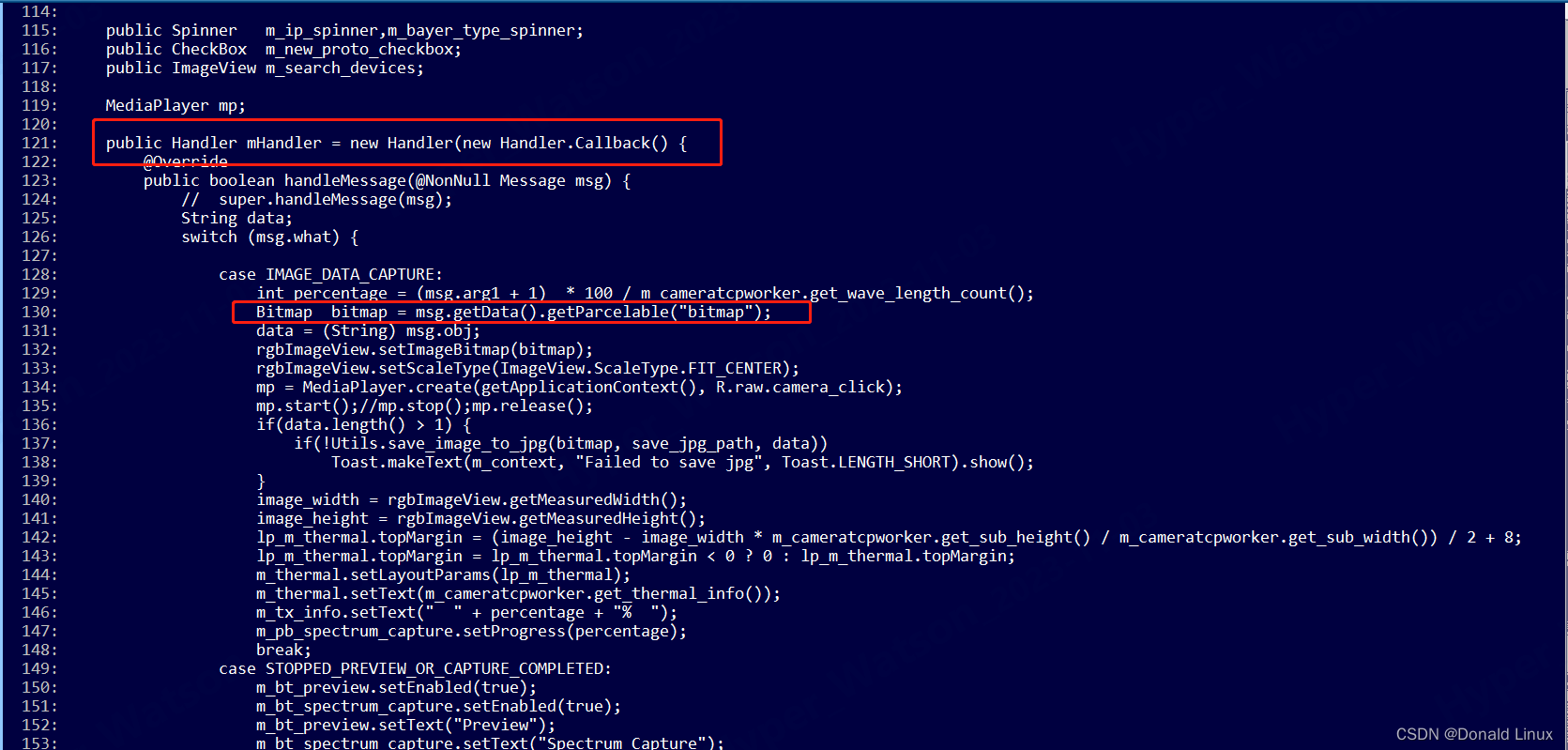
Android java Handler sendMessage使用Parcelable传递实例化对象，我这里传递Bitmap 图片数据
一、Bundle给我们提供了一个putParcelable(key,value)的方法。专门用于传递实例化对象。 二、我这里传递Bitmap 图片数据，实际使用可以成功传统图像数据。 发送：Bundle bundle new Bundle();bundle.putParcelable("bitmap",bitmap);msg.setD…...
CTF工具PDF隐写神器wbStego4open安装和详细使用方法
wbStego4open安装和详细使用方法 1.wbStego4open介绍：2.wbStego4open下载：3.wbStego4open原理图：4.wbStego4open使用教程：第一步：第二步：第三步：第四步：第五步： 5.wbSteg…...
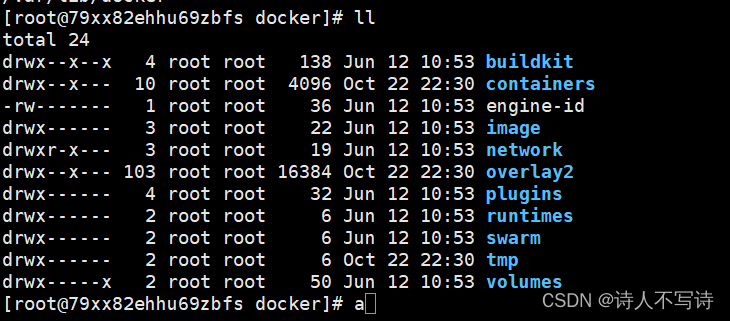
docker镜像使用
一、查看docker版本 docker version docker默认安装目录 /var/lib/docker 目录文件如下： 二、查看下载的镜像 docker images 三、下载镜像 docker pull [OPTIONS] NAME[:TAG|DIGEST] option作用-a, --all-tags拉取所有 tagged 镜像–disable-content-trust…...
【Git】git的下载安装与使用
目录 目录 一.下载安装 官方下载 淘宝镜像下载 安装 二.创建本地仓库 三.git的基本操作命令 git status git add . git commit -m " " 四.gitee(码云）的使用 配置ssh公钥 编辑 查看公钥 gitee创建仓库 将本地仓库的文件上传到远程仓库…...
, deriv(),integral()，solve()多式处理函数)
R语言中的函数27：polynom::polynomial(), deriv(),integral()，solve()多式处理函数
文章目录 介绍polynomial()用法参数实例多项式的加减乘除等运算实例 deriv()和integral()用法参数实例solve()参数实例 介绍 R语言中的polynom包可以实现对多项式的操作，例如：加、减、乘、除、微分、积分。使用的时候先用polynomial()函数定义一个多项式…...
基于STM32CubeMX和keil采用USART/UART实现非中断以及中断方式数据回环测试借助CH340以及XCOM
文章目录 前言1. 接口概述1.1 USART/UART接口1.2 串口通信参数1.3 波特率计算 2. 传输函数3. 回环测试3.1 上位机环境配置3.2 阻塞模式3.3 中断模式 4. STM32CubeMX配置4.1 时钟配置4.2 调试配置4.3 串口引脚配置4.4 工程配置 5. 测试效果6. 不借助上位机回环测试总结 前言 这…...
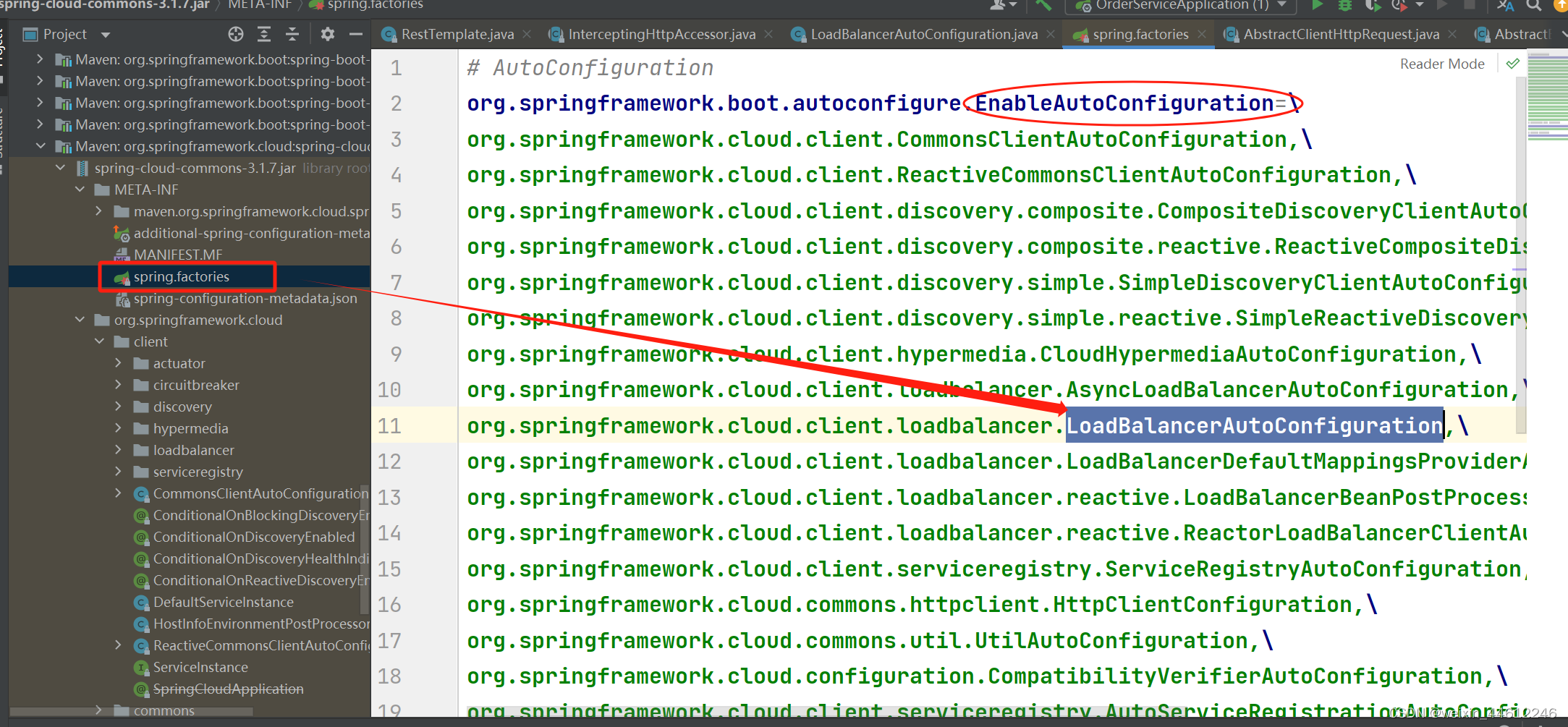
Spring cloud负载均衡 @LoadBalanced注解原理
接上一篇文章，案例代码也在上一篇文章的基础上。 在上一篇文章的案例中，我们创建了作为Eureka server的Eureka注册中心服务、作为Eureka client的userservice、orderservice。 orderservice引入RestTemplate，加入了LoadBalanced注解&#x…...
C#when关键字
在C#中，when关键字用于在模式匹配表达式中添加条件。它允许您在模式匹配的过程中指定额外的条件，以进一步过滤匹配的模式。当模式匹配和附加条件都为真时，相关的代码块将被执行。 以下是when关键字的详细解释以及示例说明： 语法…...
华为政企无线局域网产品集
产品类型产品型号产品说明 室内接入点AirEngine 5760-51AirEngine 5760-51是华为发布的支持Wi-Fi 6（802.11ax）标准的新一代室内AP，适合部署在企业办公、零售、制造等场景。 通过软件定义射频，能够在双频、三频模式灵活切换&a…...
Frozen-Flask ：将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是：将一个 Flask Web 应用生成成纯静态 HTML 文件，从而可以部署到静态网站托管服务上，如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”（简单设计）是软件开发中的一个重要理念，倡导以最简单的方式实现软件功能，以确保代码清晰易懂、易维护，并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计，遵循“让事情保…...
在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了，要么要会员、要么写的乱七八糟。这里我整理一下，把问题说清楚并且给出代码，拿去用就行，照着葫芦画瓢。 问题 在继承QWebEngineView后，重写mousePressEvent或event函数无法捕获鼠标按下事…...
20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码，而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库，可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画，可以包含在你的网页或应用项目中。 3.An…...
iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题，无需引入，直接可…...
【MATLAB代码】基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），针对传感器观测数据中存在的脉冲型异常噪声问题，通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现，验证了后者在状态估计鲁棒性方面的显著优…...
第7篇：中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中，可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中，必须做到： 🔍 追踪每一条 SQL 的生命周期（从入口到数据库执行）&#…...
【深度学习新浪潮】什么是credit assignment problem？
Credit Assignment Problem（信用分配问题） 是机器学习，尤其是强化学习（RL）中的核心挑战之一，指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中，智能体执行一系列动作后获得一个最终奖励，但每个动作对最终结果的贡献程度往往…...
【Kafka】Kafka从入门到实战：构建高吞吐量分布式消息系统
Kafka从入门到实战：构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台，最初由LinkedIn开发，后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理，能够处理来自多个生产者的海量数据，并将这些数据实时传递给消费者。 Kafka核心特…...
Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存，但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程，可以参考这篇文章，我觉得写的非常…...