[python 刷题] 1248 Count Number of Nice Subarrays
[python 刷题] 1248 Count Number of Nice Subarrays
题目如下:
Given an array of integers
numsand an integerk. A continuous subarray is called nice if there arekodd numbers on it.Return the number of nice sub-arrays.
这道题和 1343 Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold 挺像的
双指针
先声明,我的写法不是最有效的,其他的双指针/滑动窗口的解法会更加的高效,不过我感觉对我来说这么写是最好理解的
首先题目要求必须要有 k 个奇数,以题目中 Input: nums = [2,2,2,1,2,2,1,2,2,2], k = 2 为例,它的 base case 是这样的:

同时,因为两边都是偶数,因此指针是可以向两边延长的,演唱后也都是满足题目需求,即,子数组中有 k 个奇数
首先用两个指针指向 l l l 和 r r r,使用 c o u n t e r counter counter 计算 [ l , l + 1 , . . . , r ] [l, l + 1, ..., r] [l,l+1,...,r] 中的奇数。每次移动 r r r 的时候,更新 c o u n t e r counter counter,这时候会出现两个需要照顾的条件:
-
c o u n t e r > k counter > k counter>k
这个时候就需要不断移动 l l l,一直到 c o u n t e r = = k counter == k counter==k
-
c o u n t e r = = k counter == k counter==k
依旧以上面的案例来说,因为左侧指针没有动过,实际上应该是这样的情况:

这时候新建一个 t e m p temp temp 指针代替右侧指针,并且将 d i f f diff diff 保存下来:

这里的 d i f f diff diff 代表着不同的组合,即 l l l 移动一格时所会产生的不同组合,在移动左侧指针时,每次添加 d i f f diff diff 即可
代码如下:
class Solution:def numberOfSubarrays(self, nums: List[int], k: int) -> int:n = len(nums)res, count = 0, 0l, r = 0, 0while r < n:if nums[r] % 2:count += 1while count > k:if nums[l] % 2:count -= 1l += 1if count == k:res += 1t = r + 1while t < n and not nums[t] % 2:res += 1t += 1diff = t - rr = t - 1while l < r and not nums[l] % 2:res += diffl += 1r += 1return res
prefix sum
使用 prefix sum 就比较简单了,这里是将所有出现奇数的次数全都保存下来到一个变量中,同时,会形成一个 {odd_num: even_num_freq + 1} 的对应关系,这样可以保存不同的组合
如 Input: nums = [2,2,2,1,2,2,1,2,2,2], k = 2,它的键值对的关系为 {0: 4, 1: 3, 2: 4},其中保存的对应关系为:
0: [default_value, 2,2,2]
1: [1,2,2]
2: [1,2,2,2]
这样,通过 count[odd_count - k] 就能够获取对应的变化,也就是上一个解法中的 d i f f diff diff,代码如下:
class Solution:def numberOfSubarrays(self, nums: List[int], k: int) -> int:n = len(nums)# 这里使用数组而非字典,不过其原理是一样的# 使用 n + 1 是因为 0 为没有出现 odd 的情况# 而当数组中所有的成员都是 odd 时,count 的长度就为 n + 1count = [0] * (n + 1)# 这个是 base case# 空数组也是一个合法的 subarraycount[0] = 1odd_count = 0res = 0for num in nums:if num % 2 == 1:odd_count += 1if odd_count >= k:res += count[odd_count - k]count[odd_count] += 1return res
相关文章:

[python 刷题] 1248 Count Number of Nice Subarrays
[python 刷题] 1248 Count Number of Nice Subarrays 题目如下: Given an array of integers nums and an integer k. A continuous subarray is called nice if there are k odd numbers on it. Return the number of nice sub-arrays. 这道题和 1343 Number of S…...
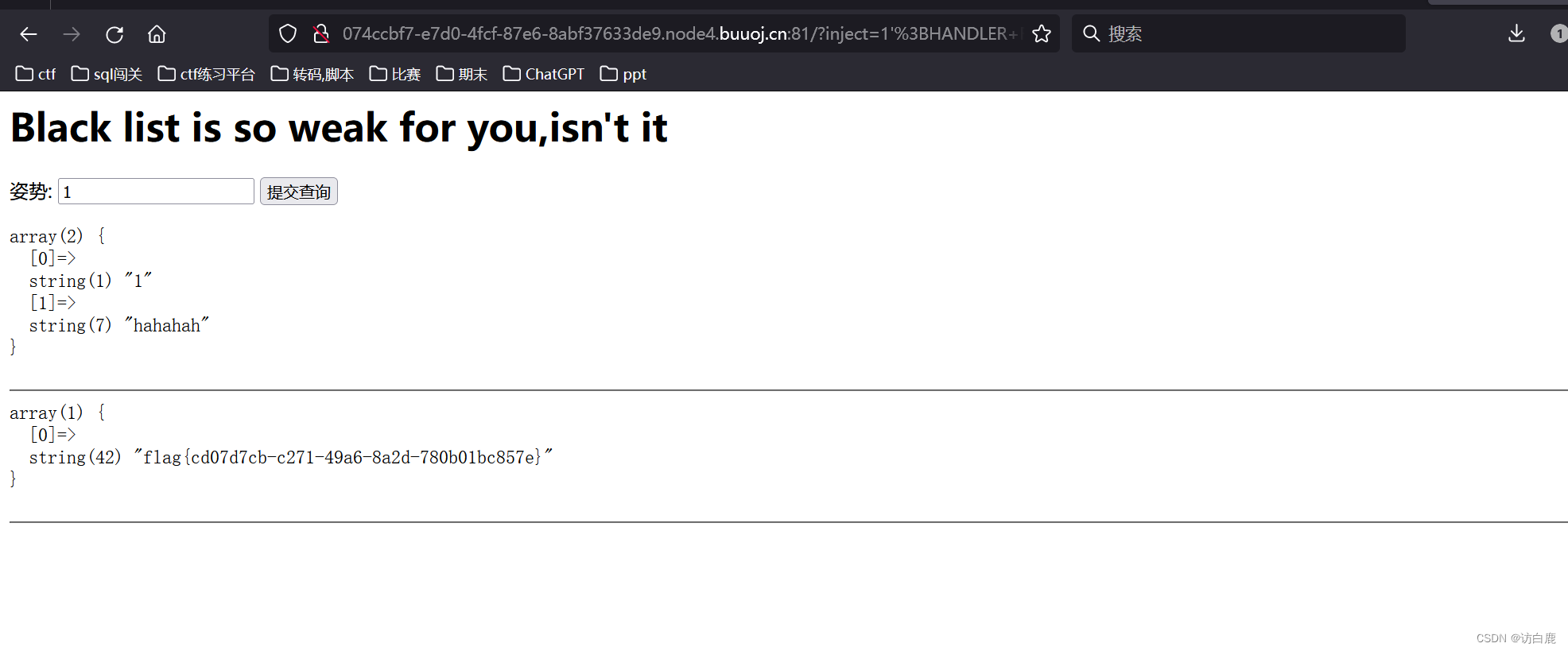
堆叠注入 [GYCTF2020]Blacklist1
打开题目 判断注入点 输入1,页面回显 输入1 页面报错 输入 1 # 页面正常,说明是单引号的字符型注入 我们输入1; show databases; # 说明有6个数据库 1; show tables; # 说明有三个表 我们直接查看FlagHere的表结构 1;desc FlagHere;# 发…...

算法:Java构建二叉树并递归实现二叉树的前序、中序、后序遍历
先自定义一下二叉树的类: // Definition for a binary tree node. public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val val;this.left…...

既然有了字节流,为什么还要有字符流?
字符流和字节流之间的区别主要在于它们处理数据的方式和用途: 字节流:字节流以字节为单位进行数据的读取和写入,适用于处理二进制数据,如图像、音频和视频文件。字节流是处理底层数据的理想选择,它不会对数据进行编码…...
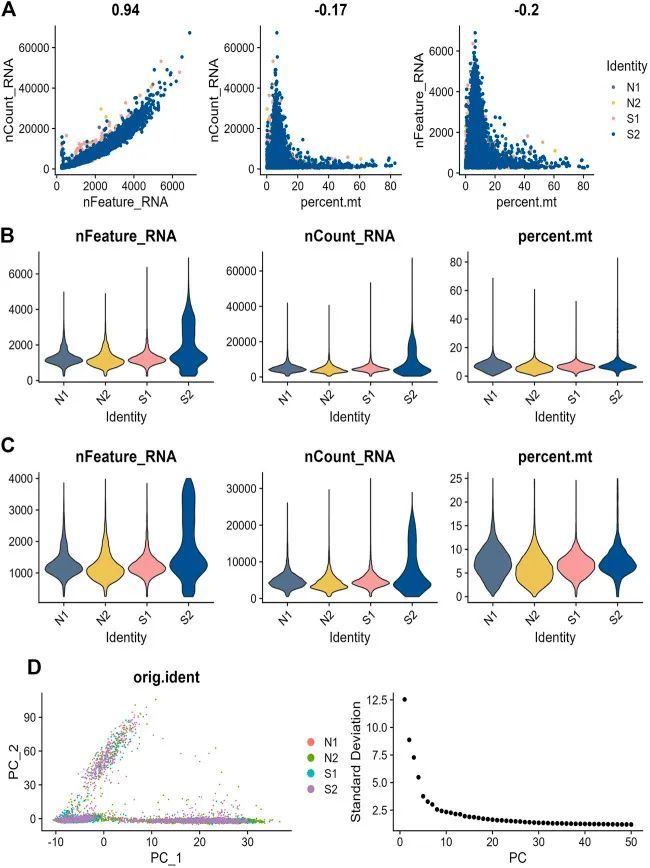
3+单细胞+代谢+WGCNA+机器学习
今天给同学们分享一篇生信文章“Identification of new co-diagnostic genes for sepsis and metabolic syndrome using single-cell data analysis and machine learning algorithms”,这篇文章发表Front Genet.期刊上,影响因子为3.7。 结果解读&#x…...
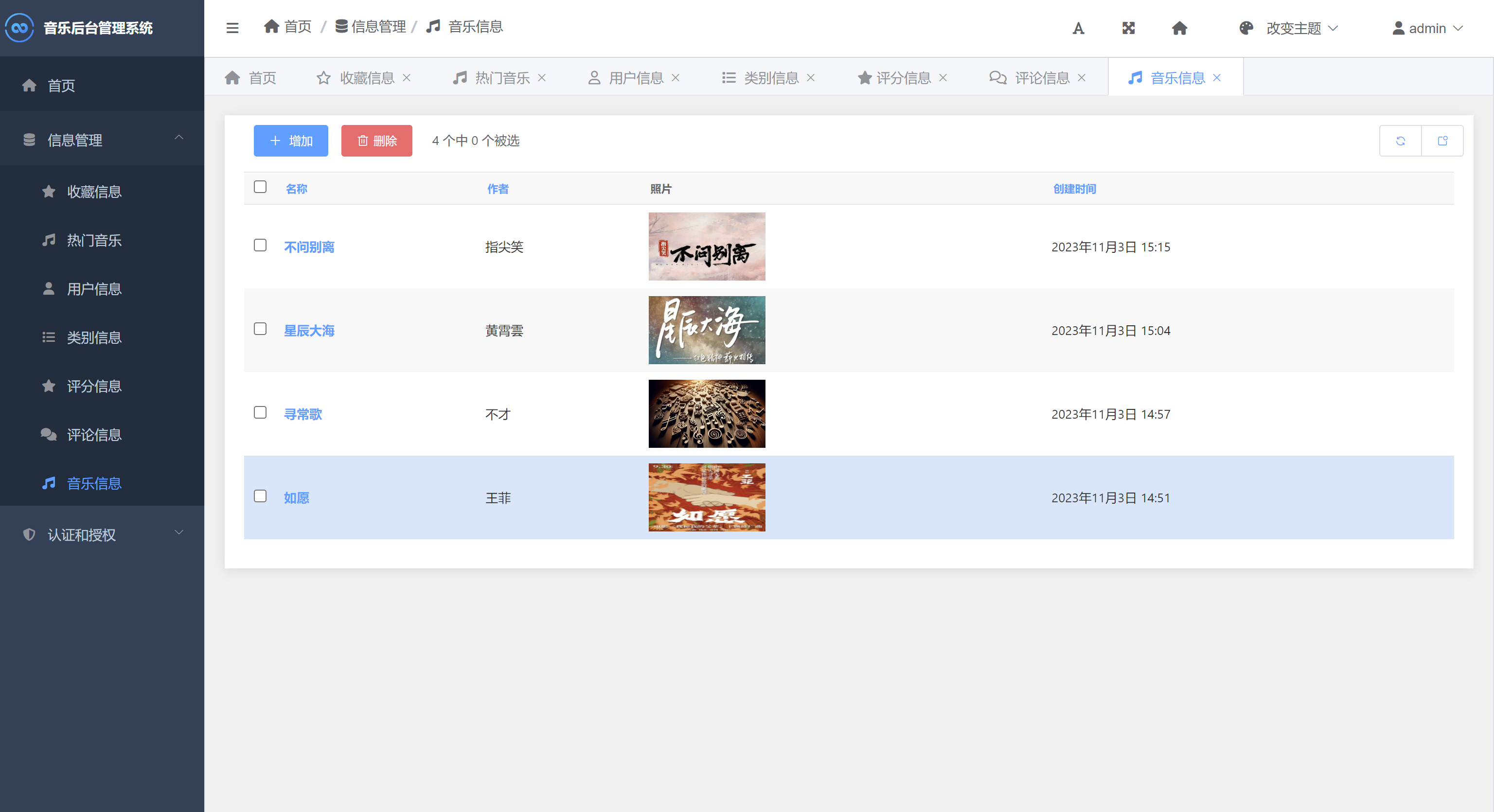
音乐推荐与管理系统Python+Django网页界面+协同过滤推荐算法
一、介绍 音乐推荐与管理系统。本系统采用Python作为主要开发语言,前端使用HTML、CSS、BootStrap等技术搭建界面平台,后端使用Django框架处理请求,并基于Ajax等技术实现前端与后端的数据通信。在音乐个性推荐功能模块中采用通过Python编写协…...
You Only Look Once: Unified, Real-Time Object Detection)
(论文阅读15/100)You Only Look Once: Unified, Real-Time Object Detection
文献阅读笔记 简介 题目 You Only Look Once: Unified, Real-Time Object Detection 作者 Joseph Redmon, Santosh Divvala, Ross Girshick, Ali Farhadi 原文链接 https://arxiv.org/pdf/1506.02640.pdf 《You Only Look Once: Unified, Real-Time Object Detection》…...

init进程启动过程
首语 init进程是Android系统中用户空间的第一个进程,进程号为1,是Android系统启动的一个关键步骤,作为第一个进程,它的主要工作是创建Zygote和启动属性服务等。init进程是由多个源文件共同组成的,源码目录在system/co…...
全网最详细的【shell脚本的入门】
🏅我是默,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Linux》。🎯🎯 🚀无论你是编程小白,还是有一定基础的程序员,这…...

CH10_简化条件逻辑
分解条件表达式(Decompose Conditional) if (!aDate.isBefore(plan.summerStart) && !aDate.isAfter(plan.summerEnd))charge quantity * plan.summerRate; elsecharge quantity * plan.regularRate plan.regularServiceCharge;if (summer())…...
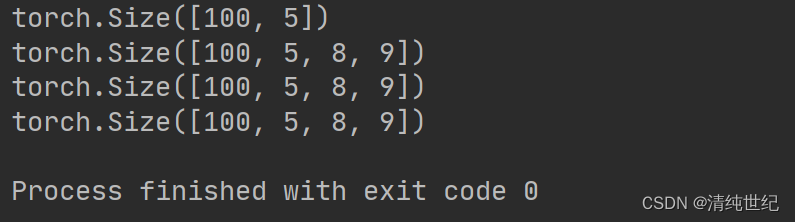
nn.LayerNorm解释
这个是层归一化。我们输入一个参数,这个参数就必须与最后一个维度对应。但是我们也可以输入多个维度,但是必须从后向前对应。 import torch import torch.nn as nna torch.rand((100,5)) c nn.LayerNorm([5]) print(c(a).shape)a torch.rand((100,5,…...

Springboot搭建微服务案例之Eureka注册中心
一、父工程依赖管理 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org…...

【MySQL】用户管理权限控制
文章目录 前言一. 用户管理1. 创建用户2. 删除用户3. 修改用户密码 二. 权限控制1. 用户授权2. 查看权限3. 回收权限 结束语 前言 MySQL的数据其实也以文件形式保存,而登录信息同样保存在文件中 MySQL的数据在Linux下默认路径是/var/lib/mysql 登录MySQL同样也可以…...

若依框架前后端分离版服务器部署,前端nginx的配置
server {listen 80;server_name 120.46.177.184;index index.php index.html index.htm default.php default.htm default.html;root /www/wwwroot/qilaike-vue/dist;#SSL-START SSL相关配置,请勿删除或修改下一行带注释的404规则#error_page 404/404.html;#SSL-END…...
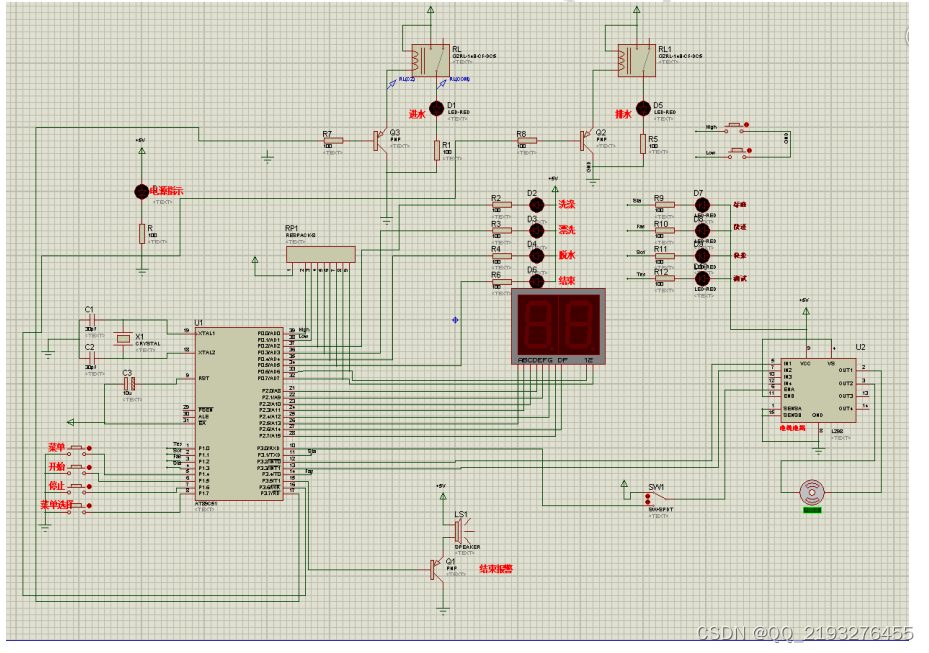
基于单片机的滚筒洗衣机智能控制系统设计
收藏和点赞,您的关注是我创作的动力 文章目录 概要 一、系统整体设计方案2.1控制系统的功能2.2设计的主要内容 二、硬件设计3.1 控制系统整体框图3.2 电源电路 三 软件设计主程序设计仿真设计 四、 结论 概要 因此我们需要一个完善的智能系统来设计一个全自动滚筒洗…...

简述多模态学习中,对齐、融合和表示
在多模态学习中,对齐、融合和表示是三个核心概念,它们相互关联,共同支持多模态数据的处理和分析。 对齐(Alignment) 对齐是多模态学习中的一个关键步骤,它涉及到如何在不同的数据模态之间发现和建立对应关…...

Kotlin 进阶函数式编程技巧
Kotlin 进阶函数式编程技巧 Kotlin 简介 软件开发环境不断变化,要求开发人员不仅适应,更要进化。Kotlin 以其简洁的语法和强大的功能迅速成为许多人进化过程中的信赖伙伴。虽然 Kotlin 的初始吸引力可能是它的简洁语法和与 Java 的互操作性,…...
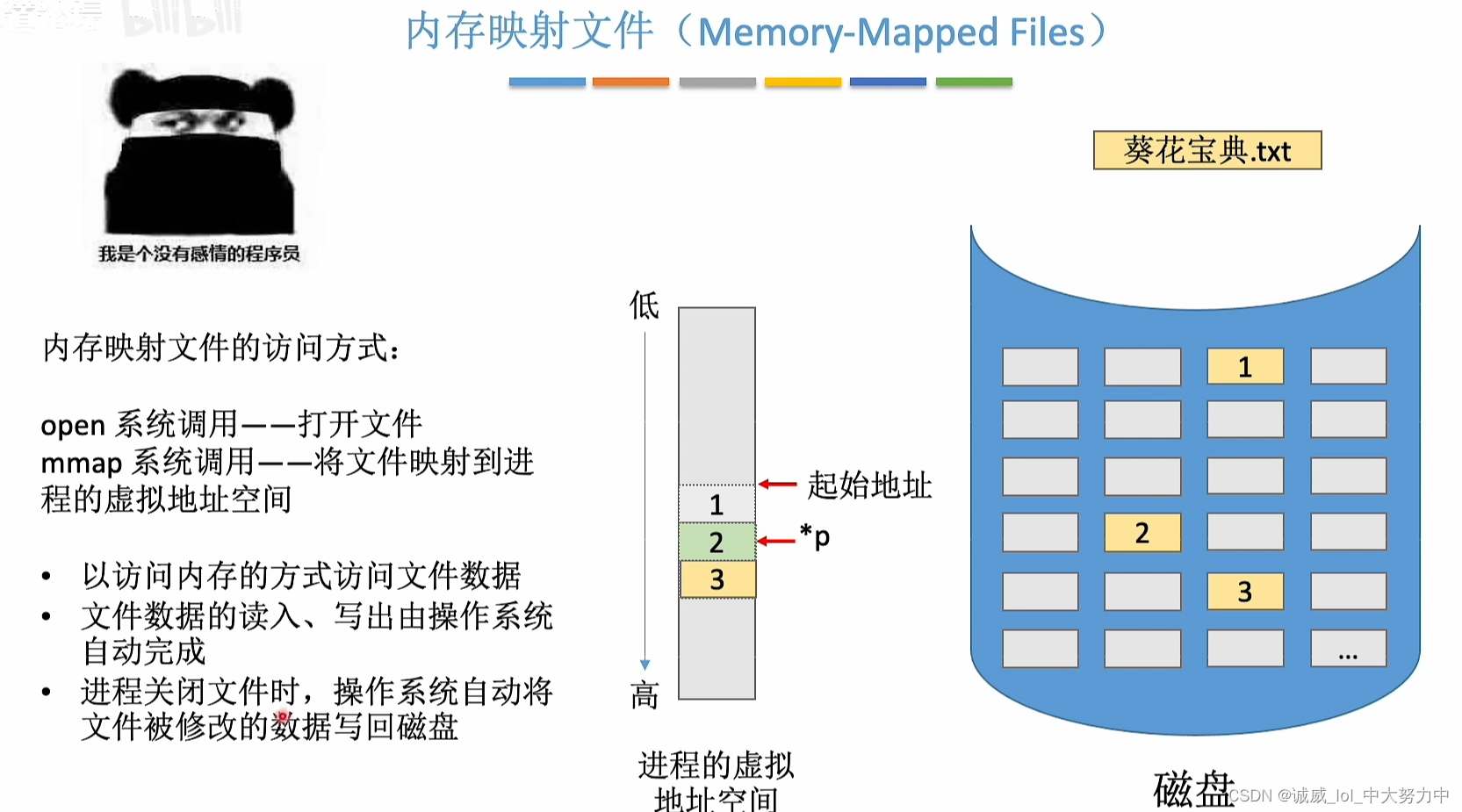
操作系统——内存映射文件(王道视频p57)
1.总体概述: 2.传统文件访问方式: 我认为,这种方式最大的劣势在于,如果要对整个文件的不同部分进行多次操作的话,这样确实开销可能会大一些,而且程序员还要指定对应的“分块”载入到内存中 3.内存映射文件…...
王道p18 07.将两个有序顺序表合并为一个新的有序顺序表,并由函数返回结果顺序表。(c语言代码实现)
视频讲解在这:👇 p18 第7题 c语言代码实现王道数据结构课后代码题_哔哩哔哩_bilibili 本题代码如下 int merge(struct sqlist* A, struct sqlist* B, struct sqlist* C) {if (A->length B->length > C->length)//大于顺序表的最大长度r…...
2024最新mac电脑清理垃圾的软件有哪些?
mac电脑是许多人喜爱的电子产品,它拥有优美的设计、流畅的操作系统和强大的性能。但是,随着使用时间的增长,mac电脑也会积累一些不必要的垃圾文件,这些文件会占用宝贵的存储空间,影响电脑的运行速度和稳定性。因此&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
