acwing算法基础之数据结构--并查集算法
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
并查集支持O(1)时间复杂度实现:
- 将两个集合合并。
- 询问两个元素是否在一个集合中。
基本原理:每个集合用一颗树来表示。树根的编号就是整个集合的编号。每个结点存储它的父结点,p[x]表示x的父结点。
问题1:如何判断树根:p[x] == x。
问题2:如何求x的集合编号:while (p[x] != x) x = p[x];。上述为朴素做法,可以通过路径压缩,进行优化。
int find(int x) {if (p[x] != x) p[x] = find(p[x]);return p[x];
}
问题3:如何合并两个集合:px是x的集合编号,py是y的集合编号:p[px] = py。
2 模板
(1)朴素并查集:int p[N]; //存储每个点的祖宗节点// 返回x的祖宗节点int find(int x){if (p[x] != x) p[x] = find(p[x]);return p[x];}// 初始化,假定节点编号是1~nfor (int i = 1; i <= n; i ++ ) p[i] = i;// 合并a和b所在的两个集合:p[find(a)] = find(b);(2)维护size的并查集:int p[N], size[N];//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量// 返回x的祖宗节点int find(int x){if (p[x] != x) p[x] = find(p[x]);return p[x];}// 初始化,假定节点编号是1~nfor (int i = 1; i <= n; i ++ ){p[i] = i;size[i] = 1;}// 合并a和b所在的两个集合:size[find(b)] += size[find(a)];p[find(a)] = find(b);(3)维护到祖宗节点距离的并查集:int p[N], d[N];//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离// 返回x的祖宗节点int find(int x){if (p[x] != x){int u = find(p[x]);d[x] += d[p[x]];p[x] = u;}return p[x];}// 初始化,假定节点编号是1~nfor (int i = 1; i <= n; i ++ ){p[i] = i;d[i] = 0;}// 合并a和b所在的两个集合:p[find(a)] = find(b);d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
3 工程化
class UnionFind {
public:UnionFind(int n) {this->n = n;p.resize(n);cnt.resize(n);d.resize(n);for (int i = 0; i < n; ++i) {p[i] = i;cnt[i] = 1;d[i] = 0;}}int find(int x) {if (x != p[x]) {int u = find(p[x]);d[x] += d[p[x]];p[x] = u;}return p[x];}void merge(int x, int y) {int px = find(x), py = find(y);if (px != py) {p[px] = py;cnt[py] += cnt[px]; }return;}int size(int x) {//返回x所在集合的大小return cnt[find(x)];}
private:int n;vector<int> p; //存储父结点vector<int> cnt; //存储集合大小,根结点的cnt才有意义vector<int> d; //存储到根结点的距离
};
相关文章:

acwing算法基础之数据结构--并查集算法
目录 1 基础知识2 模板3 工程化 1 基础知识 并查集支持O(1)时间复杂度实现: 将两个集合合并。询问两个元素是否在一个集合中。 基本原理:每个集合用一颗树来表示。树根的编号就是整个集合的编号。每个结点存储它的父结点,p[x]表示x的父结点…...
k8s:二进制搭建 Kubernetes v1.20
目录 1 操作系统初始化配置 2 部署 etcd 集群 2.1 准备签发证书环境 2.2 生成Etcd证书 3 部署 docker引擎 4 部署 Master 组件 5 部署 Worker Node 组件 k8s集群master01:192.168.30.105 kube-apiserver kube-controller-manager kube-scheduler etcd k8s集…...

SpringBoot系列-1启动流程
背景 本文作为SpringBoot系列的开篇,介绍SpringBoot的启动流程,包括Spring容器和Tomcat启动过程。SpringBoot作为流行的微服务框架,其是基于约定和自动装配机制对Spring的封装和增强。 由于前面的Spring系列对Spring容器已经进行了较为细致的…...
【记】一次common模块导入无效的bug
首先Maven clean install无用 然后idea清除缓存重启无用 pom.xml文件重载无效 正确解决路径: 1.检查common模块的父工程导入和自身模块的声明是否正确 默认是继承父工程的groupid,可以不用再声明 2.检查子工程是否引入正确的common,org不要…...
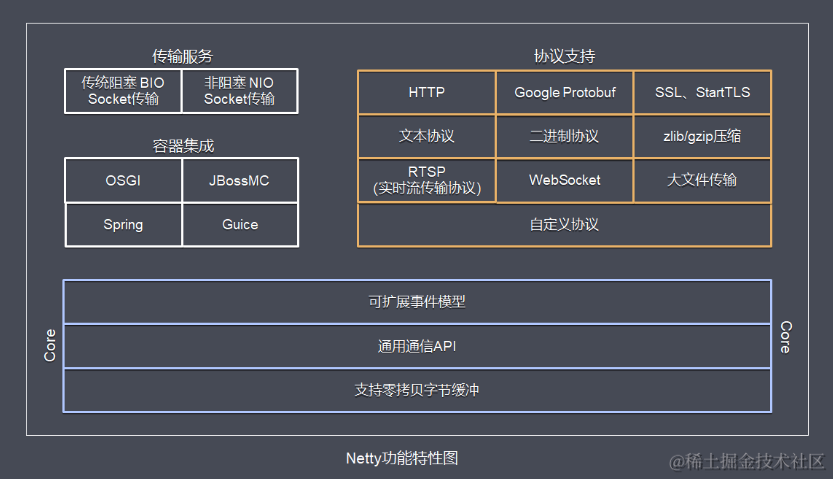
1.Netty概述
原生NIO存在的问题(Netty要解决的问题) 虽然JAVA NIO 和 JAVA AIO框架提供了多路复用IO/异步IO的支持,但是并没有提供给上层“信息格式”的良好封装。JAVA NIO 的 API 使用麻烦,需要熟练掌握 ByteBuffer、Channel、Selector等 , 所以用这些API实现一款真正的网络应…...

YOLO目标检测——真实道路车辆检测数据集【含对应voc、coco和yolo三种格式标签】
实际项目应用:自动驾驶技术研发、交通安全监控数据集说明:真实道路车辆检测数据集,真实场景的高质量图片数据,数据场景丰富标签说明:使用lableimg标注软件标注,标注框质量高,含voc(xml)、coco(j…...
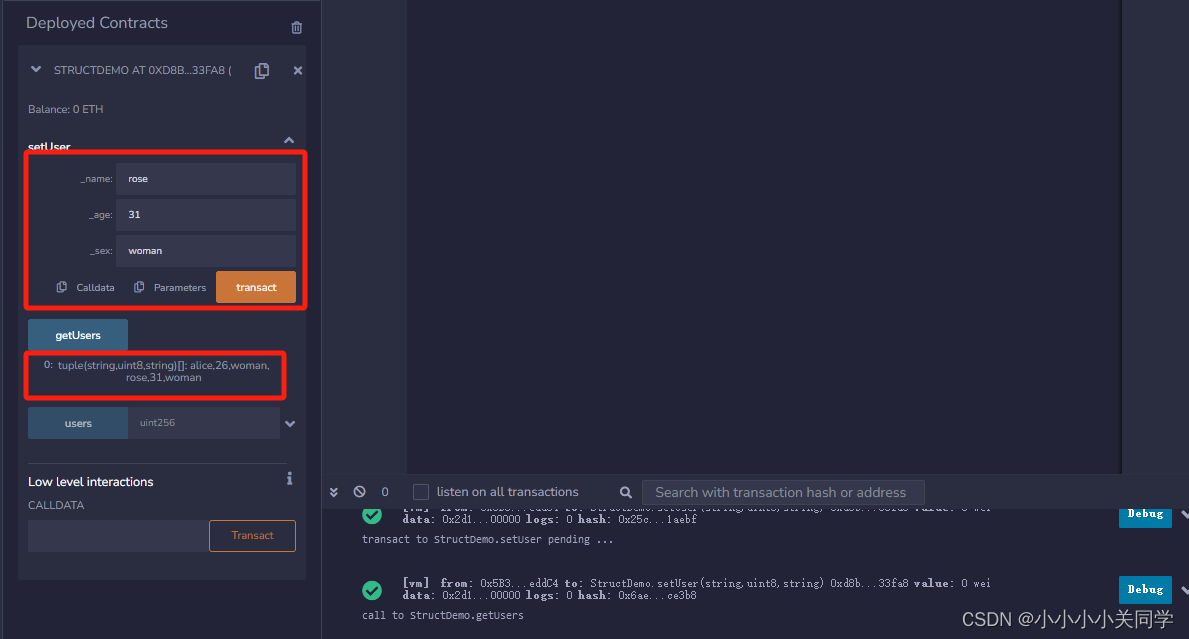
【Solidity】Solidity中的基本数据类型和复合数据类型
1. 基本数据类型 1.1 整数类型 Solidity支持有符号整数和无符号整数,可以指定位数和范围。以下是一些整数类型的示例: int:有符号整数,可以是正数或负数。2,-45,2023 uint:无符号整数&#x…...

Flutter Set存储自定义对象时 如何保证唯一
在Flutter中,Set和List是两种不同的集合类型,List中存储的元素可以重复,Set中存储的元素不可重复。 如果你想在Set中存储自定义对象,你需要确保对象的唯一性。 这可以通过在自定义类中实现hashCode方法和equals方法来实现。 has…...

Docker容器中执行throttle.sh显示权限报错:RTNETLINK answers: Operation not permitted
在模拟通信环境时,我执行了一下命令: bash ./throttle.sh wan但是,出现了权限的报错:RTNETLINK answers: Operation not permitted 解决方案说简单也挺简单,只需要两步完成。但是其实又蛮繁琐,因为需要将…...

【Linux】jdk、tomcat、MySQL环境搭建的配置安装,Linux更改后端端口
一、作用 工具的组合为开发者和系统管理员提供了构建和运行Java应用程序以及存储和管理数据的完整环境。 JDK(Java Development Kit):JDK是Java开发工具包,它提供了开发和运行Java应用程序所需的工具和库。通过安装JDK,…...
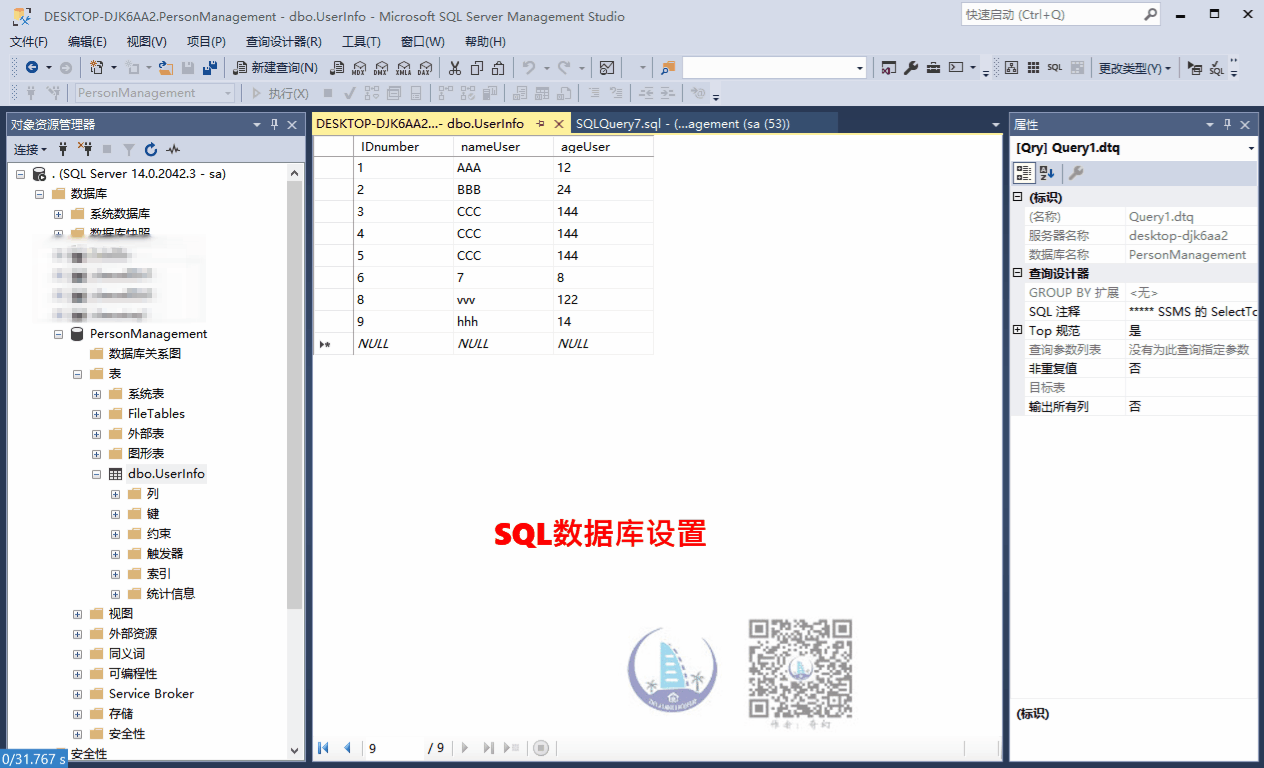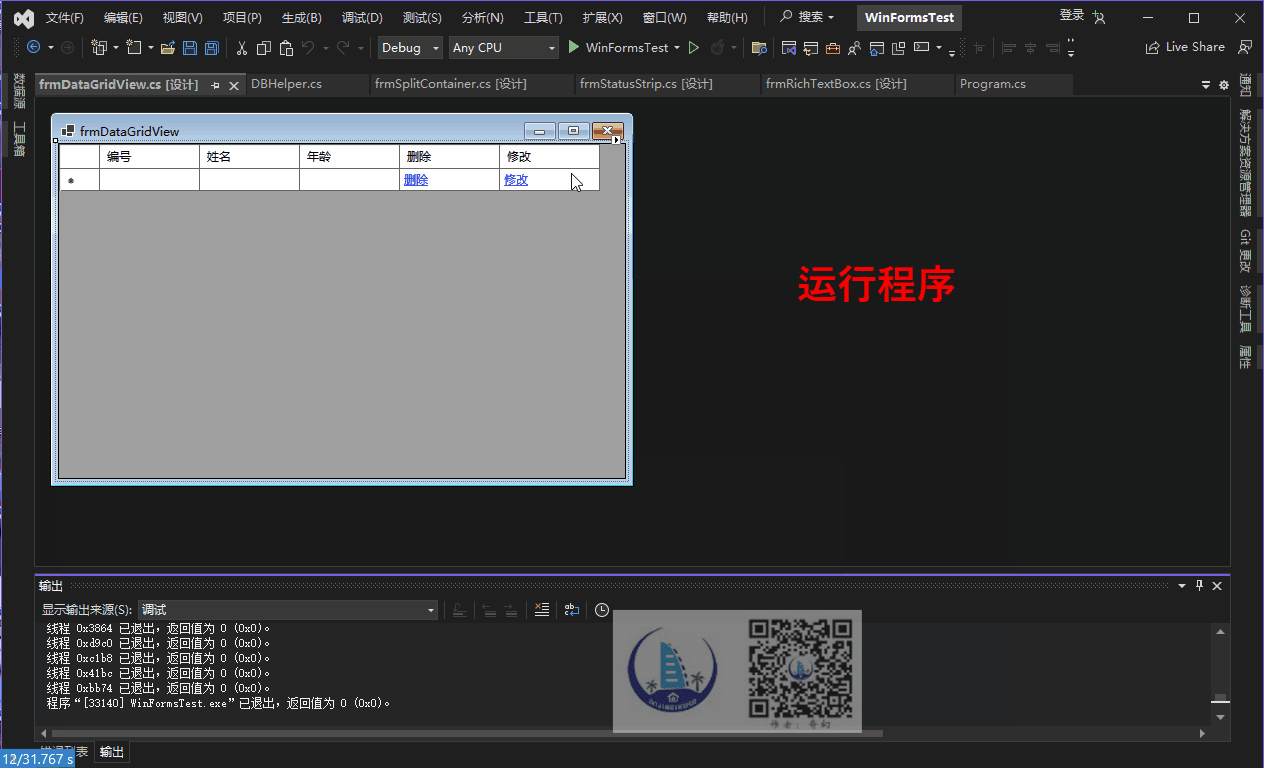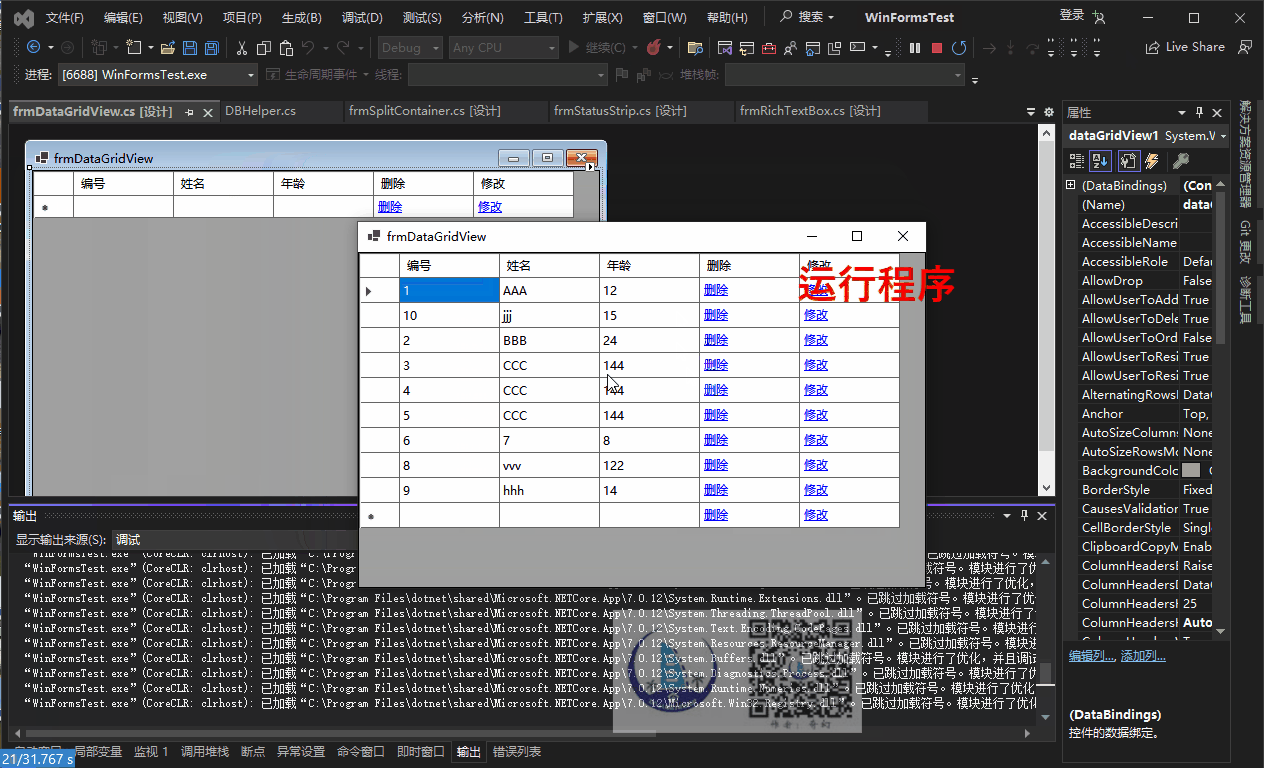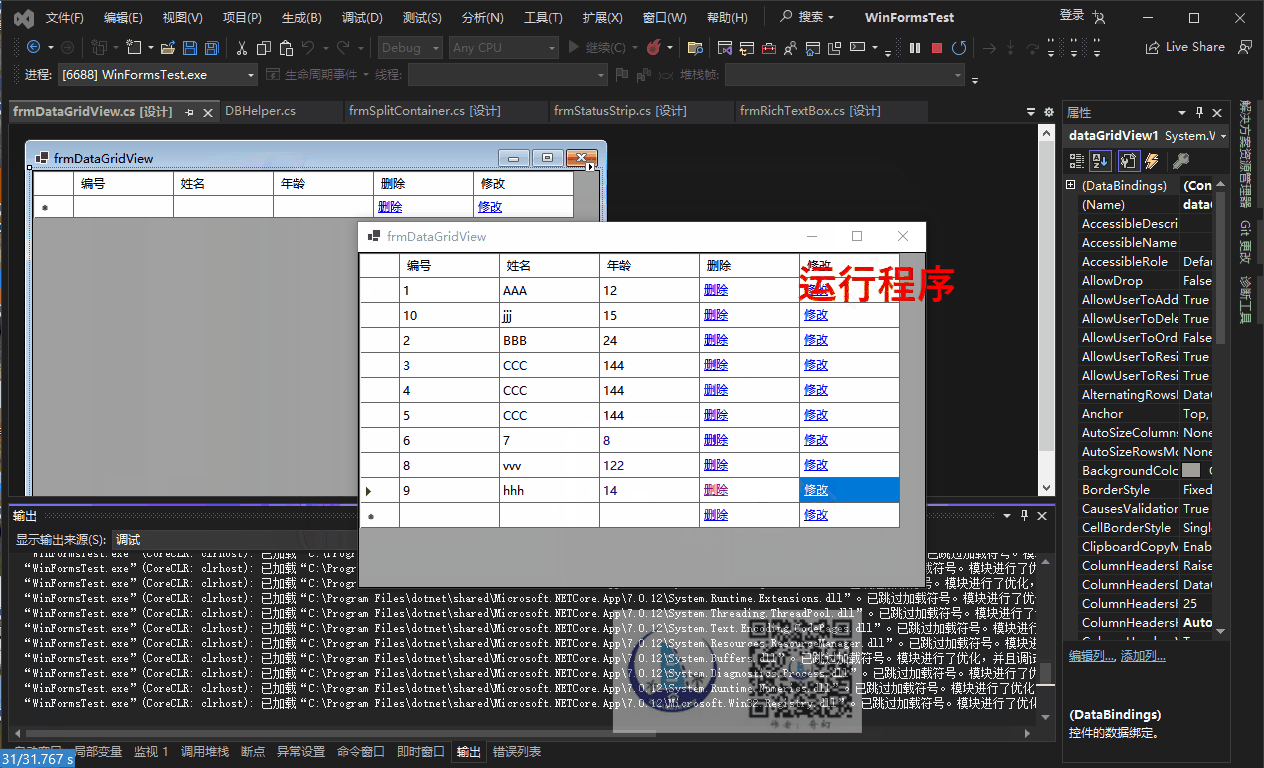
【WinForm详细教程七】WinForm中的DataGridView控件
文章目录 1.主要属性DataSource行(Row 相关属性)列(Column 相关属性)单元格(Cell 相关属性)逻辑删除AllowUserToAddRowsAllowUserToDeleteRowsAllowUserToOrderColumns其他布局和行为属性 2.控件中的行、列…...
SpringCloudTencent(上)
SpringCloudTencent 1.PolarisMesh介绍2.北极星具备的功能3.北极星包含的组件4.功能特性1.服务管理1.服务注册2.服务发现3.健康检查 2.配置管理 5.代码实战1.环境准备2.服务注册与发现3.远程调用 1.PolarisMesh介绍 1.北极星是腾讯开源的服务治理平台,致力于解决分…...
)
linux硬盘挂载(linux 修改某个磁盘挂载到新目录)
文章目录 什么是硬盘挂载linux 修改某个磁盘挂载到新目录 什么是硬盘挂载 在Linux操作系统中,挂载硬盘是将硬盘的分区或者整个硬盘与文件系统关联起来,使得我们可以通过文件系统访问硬盘中的数据。 确认硬盘信息 sudo fdisk -l该命令会列出所有已连接…...
-33)
hdlbits系列verilog解答(always块case语句)-33
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 Verilog 中的 case 语句几乎等同于 if-elseif-else 序列,该序列将一个表达式与其他表达式列表进行比较。它的语法和功能与 C 中的 switch 语句不同。 always @(*) begin // This is a combinational circuit …...
3D医学三维技术影像PACS系统源码
一、系统概述 3D医学影像PACS系统,它集影像存储服务器、影像诊断工作站及RIS报告系统于一身,主要有图像处理模块、影像数据管理模块、RIS报告模块、光盘存档模块、DICOM通讯模块、胶片打印输出等模块组成, 具有完善的影像数据库管理功能,强大…...
python 之softmx 函数
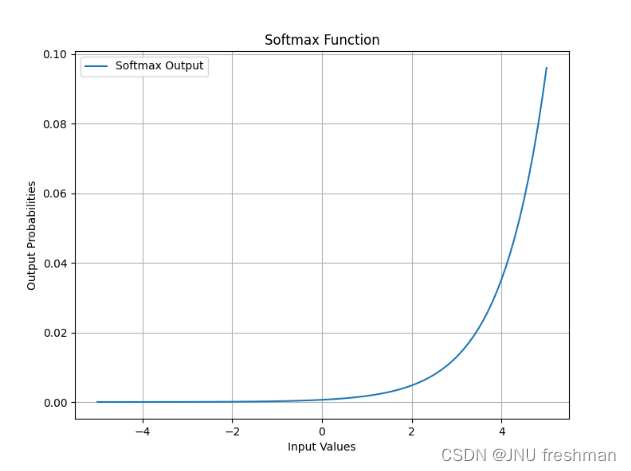
文章目录 总的介绍小应用 总的介绍 Softmax函数是一个常用的激活函数,通常用于多类别分类问题中。它将一个实数向量转换为概率分布。这个函数的输出是一个概率分布,表示输入样本属于每个可能类别的概率。 给定一个具有 (K) 个不同数值的实数向量 z (z1…...

第3章_基本select语句
文章目录 SQL概述SQL背景知识SQL分类 SQL语言的规则与规范SQL语言的规则SQL大小写规范注释命令规则(暂时了解)数据导入指令 基本的select语句select ...select ... from列的别名去除重复行空值参与运算着重号查询常数 显示表结构讲课代码课后练习 SQL概述…...

GPT3.5+文心一言+chatGLM 计算和代码生成能力简单对比
chatGLM3刚发布(10.27),打算尝试一下其code和计算能力。 共选取三个问题,难度从中等,偏困难,到困难。测试内容是正好手头上在做的事想让LLM来完成(偷懒),之前都是直接使…...

手搓一个ubuntu自动安装python3.9的sh脚本
#!/bin/bash# Step 1: 更新系统软件包 sudo apt update sudo apt upgrade -y sudo apt install -y software-properties-common# Step 2: 安装Python 3.9的依赖项 sudo apt install -y build-essential zlib1g-dev libncurses5-dev libgdbm-dev libnss3-dev libssl-dev libread…...

volte使用方法 nodejs版本切换
Volta 一种轻松管理 JavaScript 命令行工具的方法。 文档 https://docs.volta.sh/guide/ 源码 https://github.com/volta-cli/volta 命令行 安装版本 此方法运行完会配置为默认版本 volta install node 安装最新版本的node volta install node14 安装指定版本的node volta i…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
