追梦之旅【数据结构篇】——详解C语言实现二叉树
详解C语言实现二叉树~😎
- 前言🙌
- 什么是二叉树?
- 二叉树的性质总结:
- 整体实现内容分析💞
- 1.头文件的编写:🙌
- 2.功能文件的编写:🙌
- 1)前序遍历的数值来创建树——递归函数实现 😊
- 2)求树的高度函数实现 😊
- 3)求叶子数函数实现 😊
- 4)求树的总结点个数函数实现 😊
- 5)前序遍历二叉树实现 😊
- 6)中序遍历二叉树实现 😊
- 7)后序遍历二叉树实现 😊
- 8)删除二叉树函数实现 😊
- 3.测试文件编写::🙌
- 总结撒花💞

😎博客昵称:博客小梦
😊最喜欢的座右铭:全神贯注的上吧!!!
😊作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
😘博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,手把手带领大家详解C语言实现二叉树~ 利用二叉链式存储结构来完成二叉树的实现,并完成叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。都是精华内容,可不要错过哟!!!😍😍😍
什么是二叉树?
满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树的性质总结:
- 二叉树中,第 i 层最多有 2^( i-1)个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2^K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
二叉树又可以分类为许多不同的二叉树:

整体实现内容分析💞
- 利用二叉链式存储结构来完成二叉树的实现,并完成叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。
- 采用递归的思想,先是malloc开辟结点空间,然后给结点赋值,然后递归左子树然后递归右子树。这里用*表示空。最后返回生成的root指针的地址求高度,采用后序遍历的思想。
- 相当于求左右子树结点高度的最大值。每次递归加1就是计算结点数。求叶子总数时先求出左子树的叶子数再加上右子树的叶子数。求总结点数时这里直接递归计算出左子树和右子树的总结点数,每次加1表示遍历的节点数计算。然后就是前中后序的实现,这里也是用到递归的思想,最后便是将数销毁掉,malloc生成的空间要用free手动销毁。
1.头文件的编写:🙌
头文件的编写的整体思路分析:
这里用的是二叉链式存储的实现。首先是定义结构体,然后是对求叶子高度,前序遍历生成树,叶节点的个数,结点总数,前序遍历,中序遍历,后序遍历,销毁树。
#pragma once
#include"stdio.h"
#include"stdlib.h"
typedef int datatype;
typedef struct node
{datatype data;struct node* lchild, * rchild;
}tree;
tree* Creatbitree();
int Depthbitree(tree* T);
int Leaf_count(tree* T);
int Countbitree(tree* T);
int Preorder(tree* T);
int Inorder(tree* T);
int Postorder(tree* T);
tree* Delete(tree* T);2.功能文件的编写:🙌
1)前序遍历的数值来创建树——递归函数实现 😊
编写的整体思路分析:
采用递归的思想,先是malloc开辟结点空间,然后给结点赋值,然后递归左子树然后递归右子树。这里用*表示空。最后返回生成的root指针的地址
#include"BinaryTree.h"
tree* Creatbitree()//前序遍历的数值来创建树——递归
{char ch;tree* root;scanf("%c", &ch);//用于接收输入的数值 if (ch == '*') return NULL;//用*来判断是否为空 else {root = (tree*)malloc(sizeof(tree));root->data = ch;//赋值 root->lchild = Creatbitree();//左子树 root->rchild = Creatbitree();//右子树 }return root;
}
2)求树的高度函数实现 😊
编写的整体思路分析:
这里求高度,采用后序遍历的思想。相当于求左右子树结点高度的最大值。每次递归加1 就是计算结点数。
int Depthbitree(tree* T)//测量树的深度
{if (T == NULL) return 0;else {int leftheighter = Depthbitree(T->lchild);int rightheighter = Depthbitree(T->rchild);return (leftheighter > rightheighter ? leftheighter + 1 : rightheighter + 1);}
}3)求叶子数函数实现 😊
编写的整体思路分析:
代码上已表明算法思想,先求出左子树的叶子数再加上右子树的叶子数。
int Leaf_count(tree* T)//测量叶子的数量
{if (T == NULL) return 0;else if (!T->lchild && !T->rchild)//如果左右结点都为空则他就是叶子结点 return 1;else return Leaf_count(T->lchild) + Leaf_count(T->rchild);
}4)求树的总结点个数函数实现 😊
编写的整体思路分析:
这里直接递归计算出左子树和右子树的总结点数,每次加1表示遍历的节点数计算。
int Countbitree(tree* T) //测量总的结点个数
{if (T == NULL)return 0;else {return Countbitree(T->lchild) + Countbitree(T->rchild)+1;}
}5)前序遍历二叉树实现 😊
int Preorder(tree* T)//前序遍历序列 (根左右)
{if (T == NULL)return 0;else {printf("%c ", T->data);//先输出根节点 Preorder(T->lchild);Preorder(T->rchild);}
}6)中序遍历二叉树实现 😊
int Inorder(tree* T)//中序遍历序列 (左根右)
{if (T == NULL)return 0;else {Inorder(T->lchild);//先输出左孩子 printf("%c ", T->data);Inorder(T->rchild);}
}7)后序遍历二叉树实现 😊
int Postorder(tree* T)//后序遍历序列 (左右根)
{if (T == NULL)return 0;else {Postorder(T->lchild);//先输出左孩子 Postorder(T->rchild);printf("%c ", T->data);}
}8)删除二叉树函数实现 😊
tree* Delete(tree* T)//删除树
{if (T->lchild)Delete(T->lchild);else if (T->rchild)Delete(T->rchild);elsefree(T);
}3.测试文件编写::🙌
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"main()
{tree* T;T = (tree*)malloc(sizeof(tree));T->lchild = NULL;T->rchild = NULL;printf("请输入树的前序遍历序列\n");T = Creatbitree();int n = Depthbitree(T);int m = Leaf_count(T);int l = Countbitree(T);printf("树创建完成\n");printf("前序输出为\n");printf("\t\t");Preorder(T);printf("\n中序输出为\n");printf("\t\t");Inorder(T);printf("\n后序输出为\n");printf("\t\t");Postorder(T);printf("\n高度%d\n叶子%d\n总结点%d\n", n, m, l);Delete(T);printf("删除成功");
}功能测试结果展示图:

总结撒花💞
本篇文章旨在分享详解C语言实现二叉树。希望大家通过阅读此文有所收获!本次主要是对二叉树的实现,这里只要用到的思想是递归,这也是难点所在。这就要需要画图帮忙辅助理解,递归的具体每一步是如何执行的需要分析清楚。在创建树的时候可以采用前序遍历思想创建,这种思想创建是比较好理解的,也可以用其他思想创建,相对比较难理解一点。以及区分好前中后序遍历的思想,然后再编写代码。
😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘
相关文章:

追梦之旅【数据结构篇】——详解C语言实现二叉树
详解C语言实现二叉树~😎前言🙌什么是二叉树?二叉树的性质总结:整体实现内容分析💞1.头文件的编写:🙌2.功能文件的编写:🙌1)前序遍历的数值来创建树——递归函…...

独家 | Gen-1——可以改变视频风格的AI模型
翻译:吴振东校对:张睿毅本文约1000字,建议阅读3分钟 本文简单介绍了Runway公司的发展史,以及他们新推出的生成式AI模型Gen-1,可用于通过应用文本提示或者参考图像所指定的任意风格,将现有视频转换为新视频。…...
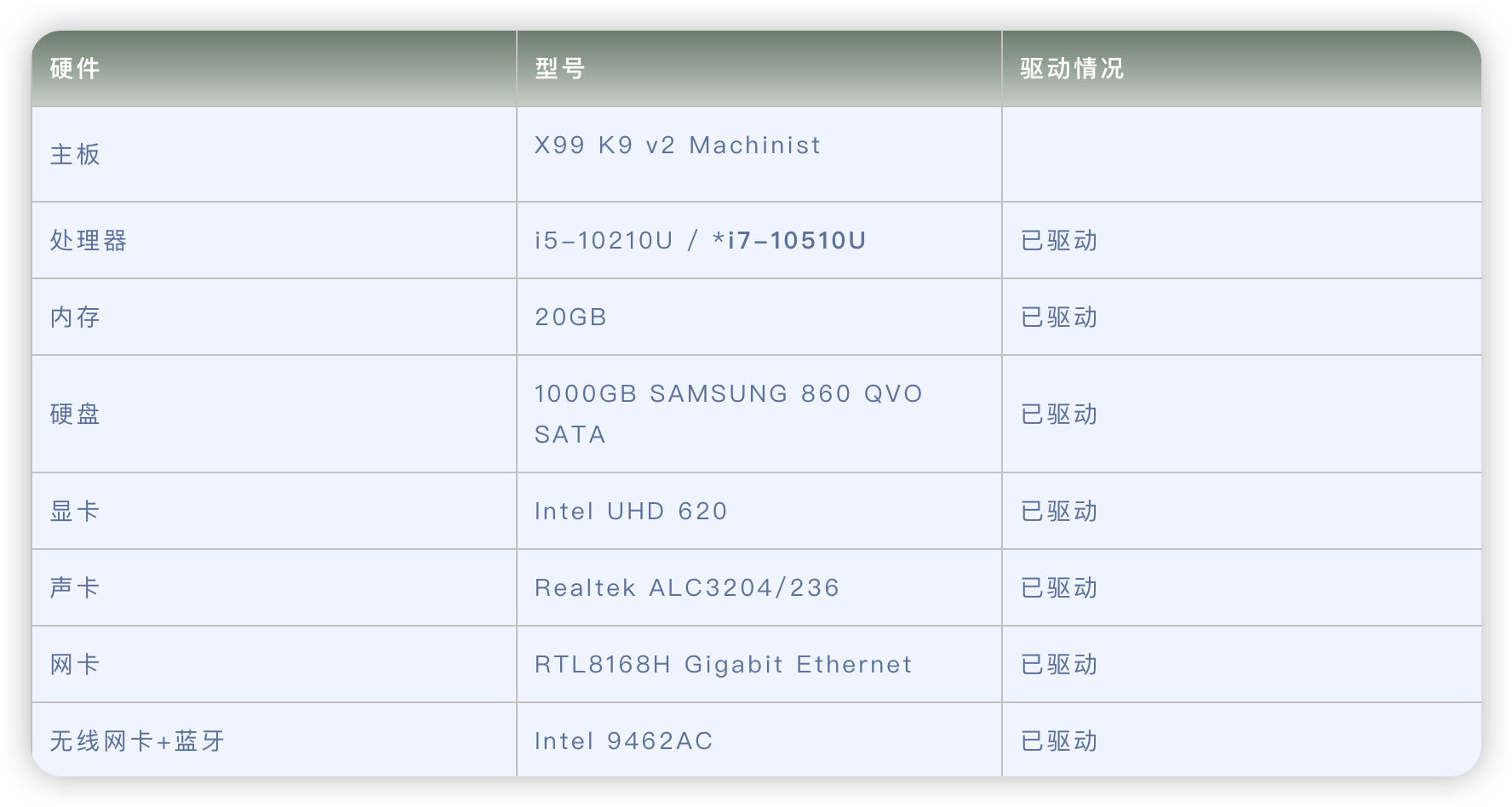
戴尔dell inspiron-5598电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板X99 K9 v2 Machinist处理器i5-10210U / *i7-10510U已驱动内存20GB已驱动硬盘1000GB SAMSUNG 860 QVO SATA已驱动显卡Intel UHD 620已驱动声卡Realtek ALC3204/236已驱动网卡RTL8168H Gigabit Ethernet已…...
3.2 网站图的爬取路径
深度优先与广度优先方法都是遍历树的一种方法,但是网站的各个网页 之间的关系未必是树的结构,它们可能组成一个复杂的图形结构,即有回路。如果在前面的网站中每个网页都加一条Home的语句,让每个网页都能回到主界面,那么…...

《SQL基础》12. SQL优化
SQL优化SQL优化数据插入insert优化大批量插入数据主键优化order by优化group by优化limit优化count优化count用法update优化SQL优化 数据插入 insert优化 如果我们需要一次性往数据库表中插入多条记录,可以从以下三个方面进行优化。 批量插入手动控制事务主键顺…...

fork之后是子进程先执行还是父进程先执行
CFS(完全公平调度器)是Linux内核2.6.23版本开始采用的进程调度器,它的基本原理是这样的:设定一个调度周期(sched_latency_ns),目标是让每个进程在这个周期内至少有机会运行一次,换一种说法就是每个进程等待CPU的时间最长不超过这个…...
)
2023年java初级面试题(5道)
一、两个对象值相同(x.equals(y) true),但却可有不同的hash code,这句话对不对?答:不对,如果两个对象x和y满足x.equals(y) true,它们的哈希码(hash code)应当相同。Java对于eqauls…...
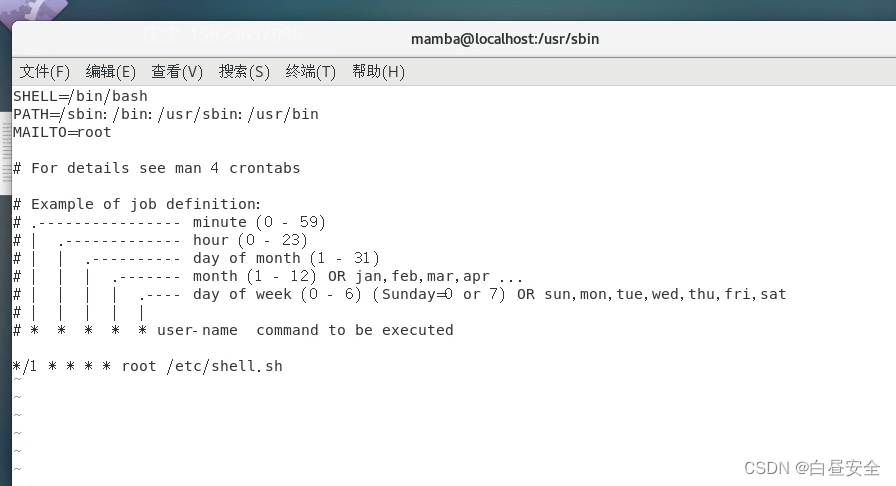
【内网安全】——Linux权限维持
作者名:白昼安全主页面链接: 主页传送门创作初心: 以后赚大钱座右铭: 不要让时代的悲哀成为你的悲哀专研方向: web安全,后渗透技术每日鸡汤: 钱至少对于现在的我来说,的确是万能的在…...

Linux 真实使用内存计算
获取Linux内存信息,可通过cat /proc/meminfo查看,比如,Ubuntu 20.04.5 LTS上会显示以下信息: leoyaDESKTOP-LMR:~$ cat /proc/meminfo MemTotal: 16017572 kB MemFree: 15637472 kB MemAvailable: 15533140 kB Bu…...
Unity Jobsystem ECS
简介随着ECS的加入,Unity基本上改变了软件开发方面的大部分方法。ECS的加入预示着OOP方法的结束。随着实体组件系统ECS的到来,我们在Unity开发中曾使用的大量实践方法都必须进行改变以适应ECS,也许不少人需要些时间适应ECS的使用,…...

Java中创建线程有哪几种方式
1.继承Thread类 总结:通过继承 Thread 类,重写 run() 方法,而不是 start() 方法 Thread 类底层实现 Runnable 接口类只能单继承 接口可以多继承2.实现Runnable接口 总结:通过实现 Runnable 接口,实现 run() 方法,依然…...
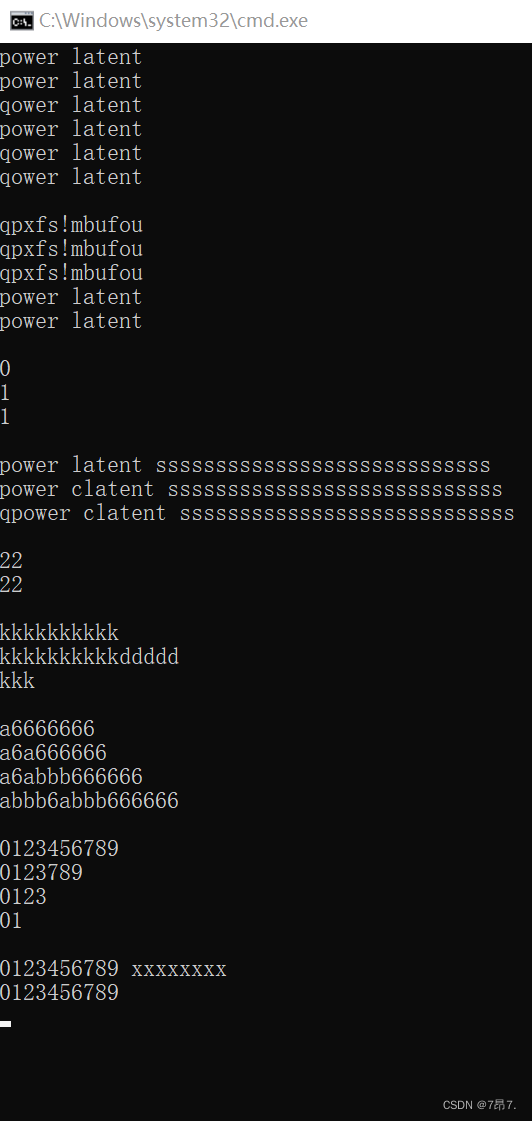
C++【string类用法详细介绍string类模拟实现解析】
文章目录string 类用法介绍及模拟实现一、string介绍二、string类常用接口1. string类对象的常见构造接口2.string类对象的常见容量接口3.string类对象的常见修改接口4. string类对象的常见访问及遍历接口5.string其他接口1.不常用查找接口2.字符替换3.字符串拼接4.字符串排序5…...

常见的开发模型和测试模型
软件的生命周期软件开发阶段的生命周期需求分析->计划->设计->编码->测试->运维软件测试阶段的生命周期需求分期->测试计划->测试设计与开发->执行测试->测试评估开发模型瀑布模型可以看到,这个模型和我们上面的软件开发生命周期很相似采用的是线性…...

印度和印度尼西亚有什么关系吗?
印度和印度尼西亚,这两个国家很多人都比较熟悉。因为两国都是人口大国,而且经济总量也比较高,在全球还是有很大影响的。不过很多人刚看到这两个国家的时候,都会觉得这两个国家肯定有什么关系,要不然国名也不会这么像。…...
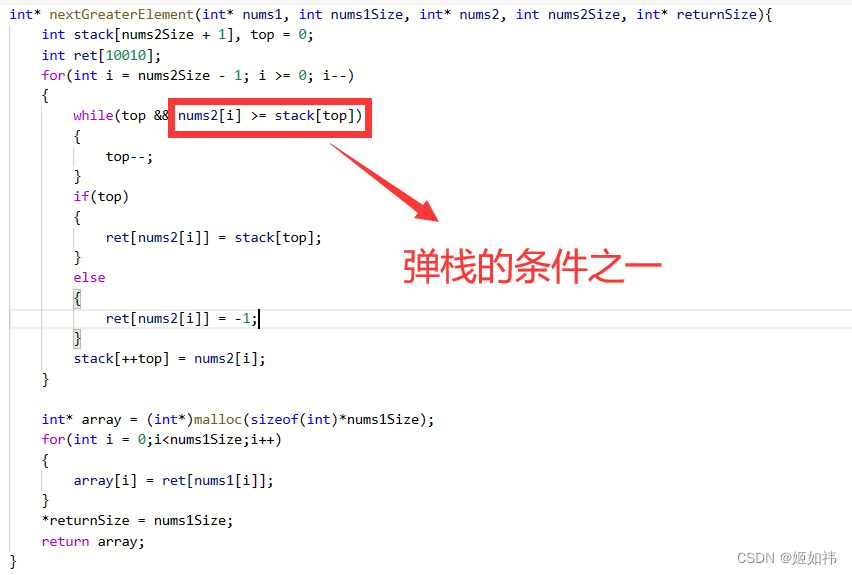
单调栈(C/C++)
目录 1. 单调栈的定义 2. 单调栈的常见用途 3. 案例分析 3.1 暴力解法 3.2 单调栈 4. 单调栈总结 1. 单调栈的定义 单调栈顾名思义,就是栈内的元素是单调的。根据栈内元素的单调性的不同,可以分为: 单调递增栈:栈内元素是单…...

算法设计与智能计算 || 专题一: 算法基础
专题一: 算法基础 文章目录专题一: 算法基础1. 算法的定义及特点1.1 算法的基本特征1.2 算法的基本要素1.3 算法的评定2 算法常见执行方法2.1 判断语句2.2 循环语句2.3 综合运用3. 计算复杂度4. 代码的重用5. 类函数的定义与使用5.1 定义类5.2 调用类函数1. 算法的定义及特点 …...

用javascript分类刷leetcode13.单调栈(图文视频讲解)
239. 滑动窗口最大值 (hard) 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1: 输入:nums [1,…...

英语基础语法学习(B站英语电力公司)
1. 句子结构 五大基本句型: 主谓主谓宾主谓宾宾主谓宾宾补主系表 谓语: 一般来说,谓语是指主语发出的动作。(动词)但是很多句子是没有动作的,但是还是必须要有谓语。(此时需要be动词&#x…...
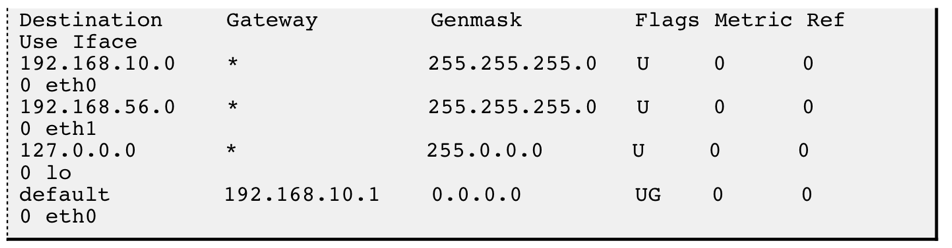
【计算机网络】网络层IP协议
文章目录一、认识IP协议二、IP协议头部格式三、IP地址划分1. IP地址分类2. 子网划分四、IP地址数量危机1. IP地址的数量限制2. NAT技术五、私网IP和公网IP六、路由1. 认识路由2. 路由表生成算法一、认识IP协议 IP协议是Internet Protocol(互联网协议)的…...

Eclipse快捷键大全
编辑类快捷键Ctrl1: 快速修复(最经典的快捷键, 可以解决很多问题, 比如import类、try catch包围等)CtrlShiftF: 格式化当前代码CtrlShiftM: 添加类的import导入CtrlShiftO: 组织类的导入(既有CtrlShiftM的作用,又可以去除没用的导入, 一般用这个导入包)CtrlY: 重做(与CtrlZ相反…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

