单调栈(C/C++)
目录
1. 单调栈的定义
2. 单调栈的常见用途
3. 案例分析
3.1 暴力解法
3.2 单调栈
4. 单调栈总结
1. 单调栈的定义
单调栈顾名思义,就是栈内的元素是单调的。根据栈内元素的单调性的不同,可以分为:
单调递增栈:栈内元素是单调递增的栈。
单调递减栈:栈内元素是单调递减的栈。
2. 单调栈的常见用途
单调栈的用途:给定一个序列,指定一个序列中的元素,求解该元素 左侧/右侧 第一个比自身 小/大的元素。
这便是单调栈的常见用途。下面结合具体的例子来理解单调栈哈!N
3. 案例分析
原题链接:
496. 下一个更大元素 I - 力扣(LeetCode)
https://leetcode.cn/problems/next-greater-element-i/
题目描述:
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
3.1 暴力解法
暴力解法的思路就比较简单了。我们先初始化一个数组 ret,用他的下标表示 nums2 中的每一个元素,对应下标的值表示右侧第一个比它大的元素。然后从后往前(从前向后也行的)遍历 nums2 数组中的元素,遍历每一个元素时向后找比该元素更大的数,如果找到则将对应的结果保存到 下标为遍历元素的位置处,如果没有找到的话就将 -1 保存到下标为遍历元素的位置处。

得到了 nums2 数组中每个元素的右边第一个比自身大的元素后,只需要遍历一次 nums1 数组,在 ret 数组中找到结果就行啦!!
假设 nums2 数组的大小为 N,在求 nums2 数组中的每一个元素右侧第一个比自身大的数时,时间复杂度是一个等差数列的求和,即 O(N*N) 。在遍历 nums1 数组时,因为 nums1 数组中的元素是nums2 数组中元素的子集,遍历 nums1 的时间复杂度为 O(N),所以总的时间复杂度为:O(N^2)。
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize)
{int ret[10010];int j;for(int i = nums2Size - 1; i>=0;i--){for(j = i + 1; j < nums2Size; j++){if(nums2[j] > nums2[i]){ret[nums2[i]] = nums2[j];break;}}if(j == nums2Size){ret[nums2[i]] = -1;}}*returnSize = nums1Size;int* array = (int*)malloc(sizeof(int)*nums1Size);for(int i = 0;i<nums1Size;i++){array[i] = ret[nums1[i]];}return array;
}

3.2 单调栈
单调栈的应用思路和双指针算法大体思路是一致的。先分析暴力解法怎么做,然后分析具体题目,找到其中隐藏的性质,从而达到优化时间效率的目的。
emm怎么分析的就不说了,后面会总结的。经过分析该问题发现:在向右找比自身大的元素时,哪些下标更大的,但是值却更小的元素是不可能作为结果输出到 ret 数组的。

分析到这里我们就可以用单调栈(为啥呢?找的是右侧第一个比自身大的元素,第一这两个字很能说明问题)来解决问题了!!我们这里使用的是用数组模拟的栈哈!效率比STL更高一点。向右找比自身大元素时,需要从后往前遍历 nums2 数组。
我们还是以上面的 3 4 7 2 5 来举例分析,开始遍历到 5 这个元素,此时栈为空,那就表明 5 这个元素右侧没有比自身大的元素(这里也能够说明为啥向右找需要从后往前遍历),将结果保存到 ret 数组。然后将 5 压入栈中。遍历到 2 时发现 2 小于栈顶的元素 5,表明 2 这个元素右侧第一个比自身大的元素是 5,将结果保存到 ret 数组中。遍历到 7 时,发现 7 大于栈顶的元素 2,这就是我们刚才说的,2 是不可能作为结果输出的,所以需要将栈顶的 2 弹出。弹出之后栈顶的元素就是 5 啦,同样 小于 7,但下标大于 7 的下标,需要再次弹出。此时我们发现栈里面已经没有元素了,说明 7 的右侧没有比自身大的元素 返回 -1。然后将 7 压入栈中。其他的元素就同理啦!
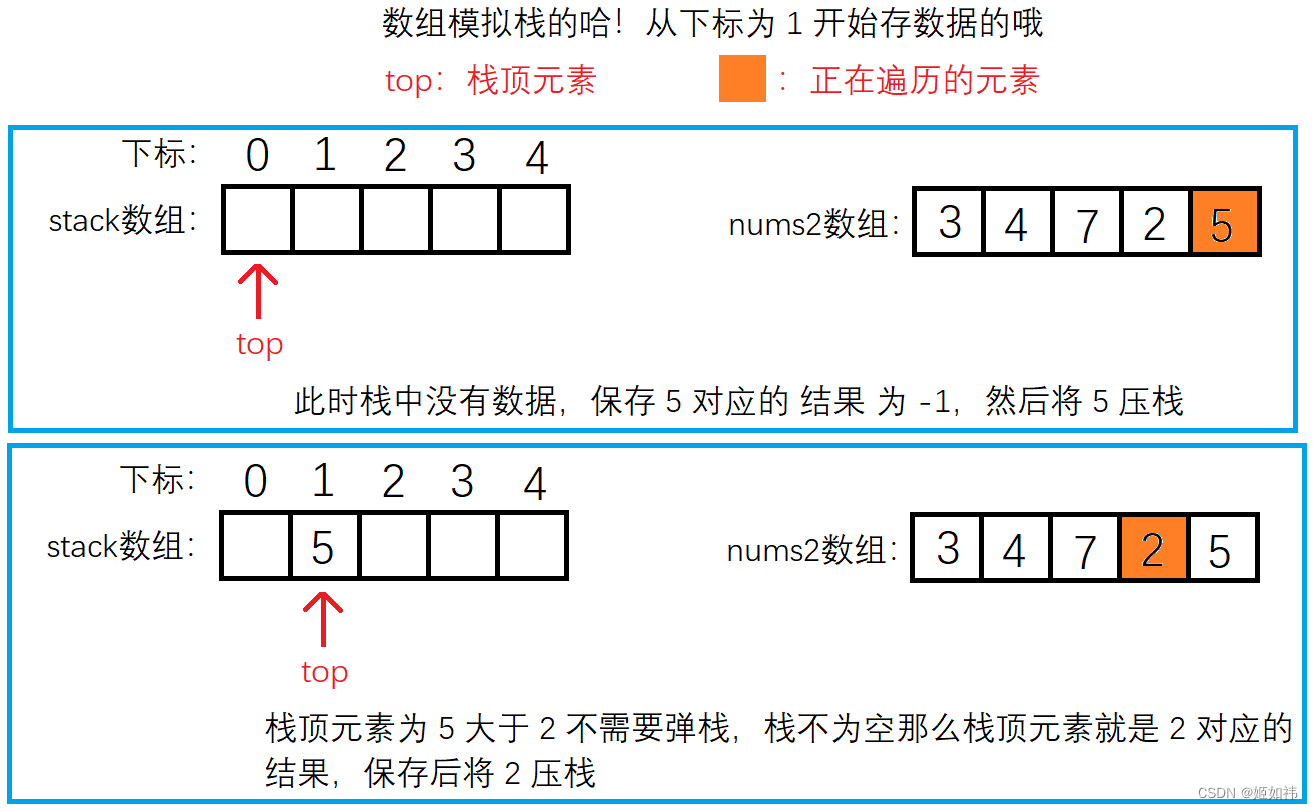
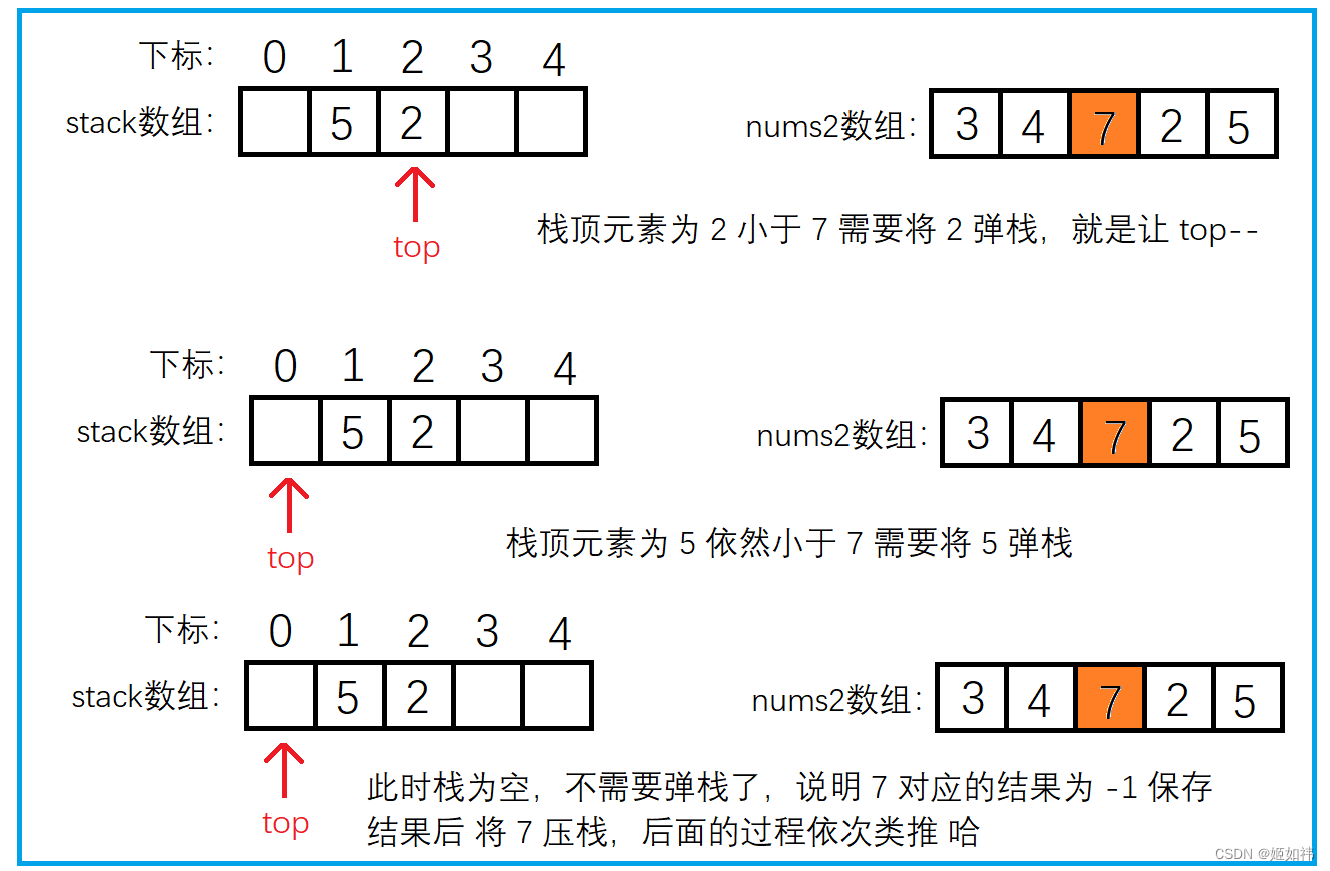
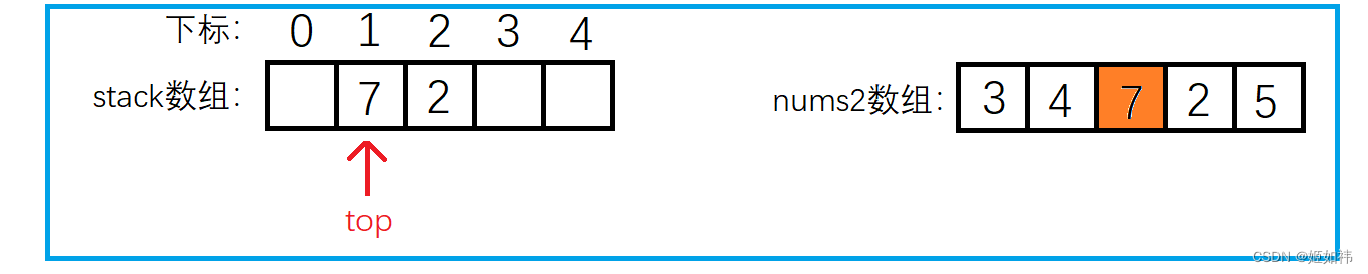
同样假设 nums2 数组的大小为 N,我们经过分析不难发现,nums2 中的元素 最多被 压栈一次,弹栈一次,所以找 nums2 数组中 右侧第一个 比自身大的数的时间复杂度为 O(N),遍历nums1数组输出结果时也是 O(N),因此总的时间复杂度就是 O(N)。
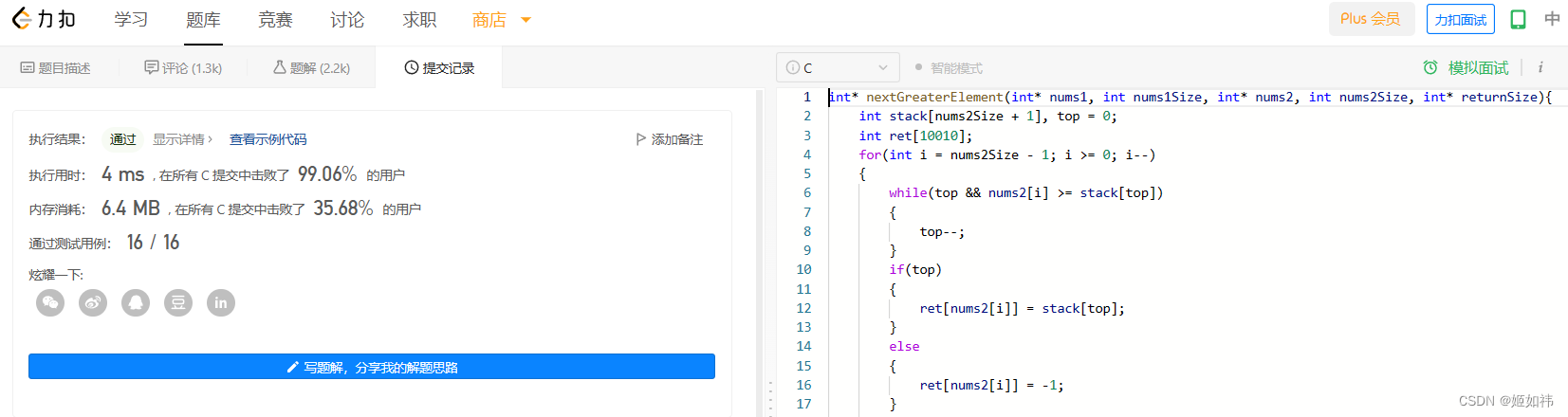
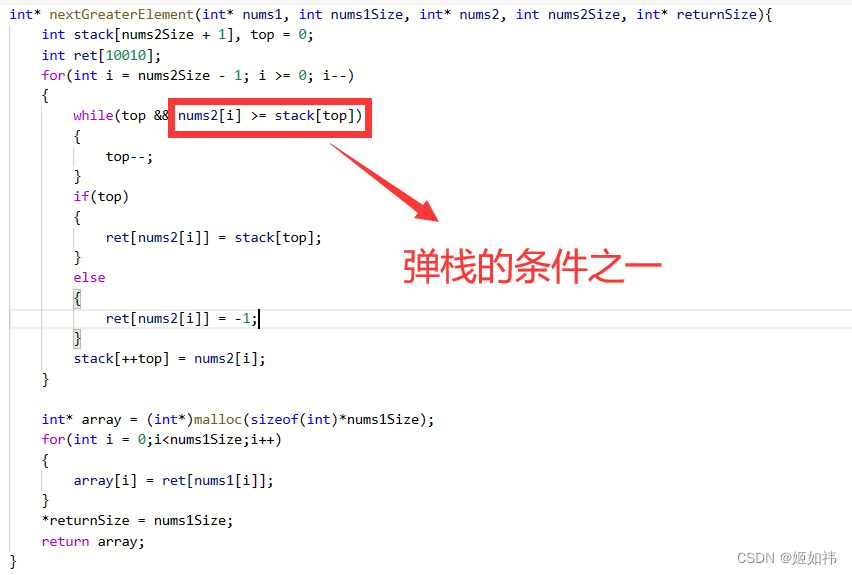
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize){int stack[nums2Size + 1], top = 0;int ret[10010];for(int i = nums2Size - 1; i >= 0; i--){while(top && nums2[i] >= stack[top]){top--;}if(top){ret[nums2[i]] = stack[top];}else{ret[nums2[i]] = -1;}stack[++top] = nums2[i];}int* array = (int*)malloc(sizeof(int)*nums1Size);for(int i = 0;i<nums1Size;i++){array[i] = ret[nums1[i]];}*returnSize = nums1Size;return array;
}
4. 单调栈总结
单调栈的常见用途就是这个啦!显然是有四种情况的:
1:向左找第一个比自身大的数。
2:向左找第一个比自身小的数。
3:向右找第一个比自身大的数。
4:向右找第一个比自身小的数。
通过以上的解题我们可能会有以下问题:
1:从前往后遍历还是从后往前遍历?
答:向右找数从后往前遍历,向左找数从前往后遍历。
2:弹栈的条件之一是大于等于还是小于等于?
答:找比自身大的数是大于等于正在遍历的数,找比自身小的数是小于等于正在遍历的数。
相关文章:

单调栈(C/C++)
目录 1. 单调栈的定义 2. 单调栈的常见用途 3. 案例分析 3.1 暴力解法 3.2 单调栈 4. 单调栈总结 1. 单调栈的定义 单调栈顾名思义,就是栈内的元素是单调的。根据栈内元素的单调性的不同,可以分为: 单调递增栈:栈内元素是单…...

算法设计与智能计算 || 专题一: 算法基础
专题一: 算法基础 文章目录专题一: 算法基础1. 算法的定义及特点1.1 算法的基本特征1.2 算法的基本要素1.3 算法的评定2 算法常见执行方法2.1 判断语句2.2 循环语句2.3 综合运用3. 计算复杂度4. 代码的重用5. 类函数的定义与使用5.1 定义类5.2 调用类函数1. 算法的定义及特点 …...

用javascript分类刷leetcode13.单调栈(图文视频讲解)
239. 滑动窗口最大值 (hard) 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1: 输入:nums [1,…...

英语基础语法学习(B站英语电力公司)
1. 句子结构 五大基本句型: 主谓主谓宾主谓宾宾主谓宾宾补主系表 谓语: 一般来说,谓语是指主语发出的动作。(动词)但是很多句子是没有动作的,但是还是必须要有谓语。(此时需要be动词&#x…...
【计算机网络】网络层IP协议
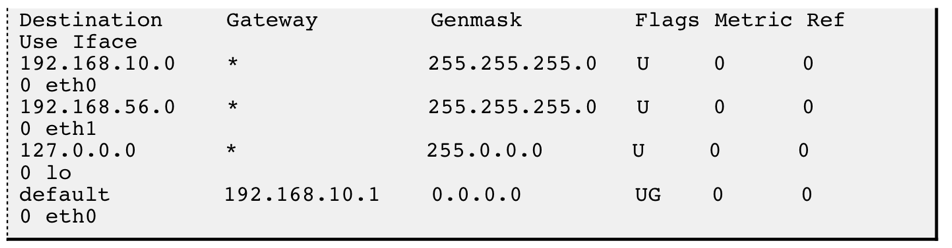
文章目录一、认识IP协议二、IP协议头部格式三、IP地址划分1. IP地址分类2. 子网划分四、IP地址数量危机1. IP地址的数量限制2. NAT技术五、私网IP和公网IP六、路由1. 认识路由2. 路由表生成算法一、认识IP协议 IP协议是Internet Protocol(互联网协议)的…...

Eclipse快捷键大全
编辑类快捷键Ctrl1: 快速修复(最经典的快捷键, 可以解决很多问题, 比如import类、try catch包围等)CtrlShiftF: 格式化当前代码CtrlShiftM: 添加类的import导入CtrlShiftO: 组织类的导入(既有CtrlShiftM的作用,又可以去除没用的导入, 一般用这个导入包)CtrlY: 重做(与CtrlZ相反…...
JavaScript 高级2 :构造函数和原型 d331702016e84f54b3594ae05e0eeac
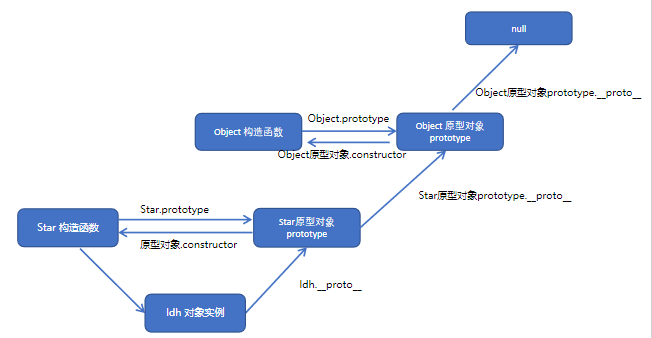
JavaScript 高级2 :构造函数和原型 Date: January 16, 2023 Text: 构造函数和原型、继承、ES5中的新增方法 目标 能够使用构造函数创建对象 能够说出原型的作用 能够说出访问对象成员的规则 能够使用 ES5新增的一些方法 构造函数和原型 概述 在典型的 OOP 的…...

maven-war-plugin插件 overlays maven-war-plugin翻译
说明 翻译maven-war-plugin插件的部分内容 官方地址为:https://maven.apache.org/plugins/maven-war-plugin/index.html Overview 概述 Introduction 介绍 Apache Maven WAR Plugin apache maven war 插件 The WAR Plugin is responsible for collecting all artifa…...
【数据结构】初识二叉树(二叉树的入门知识)
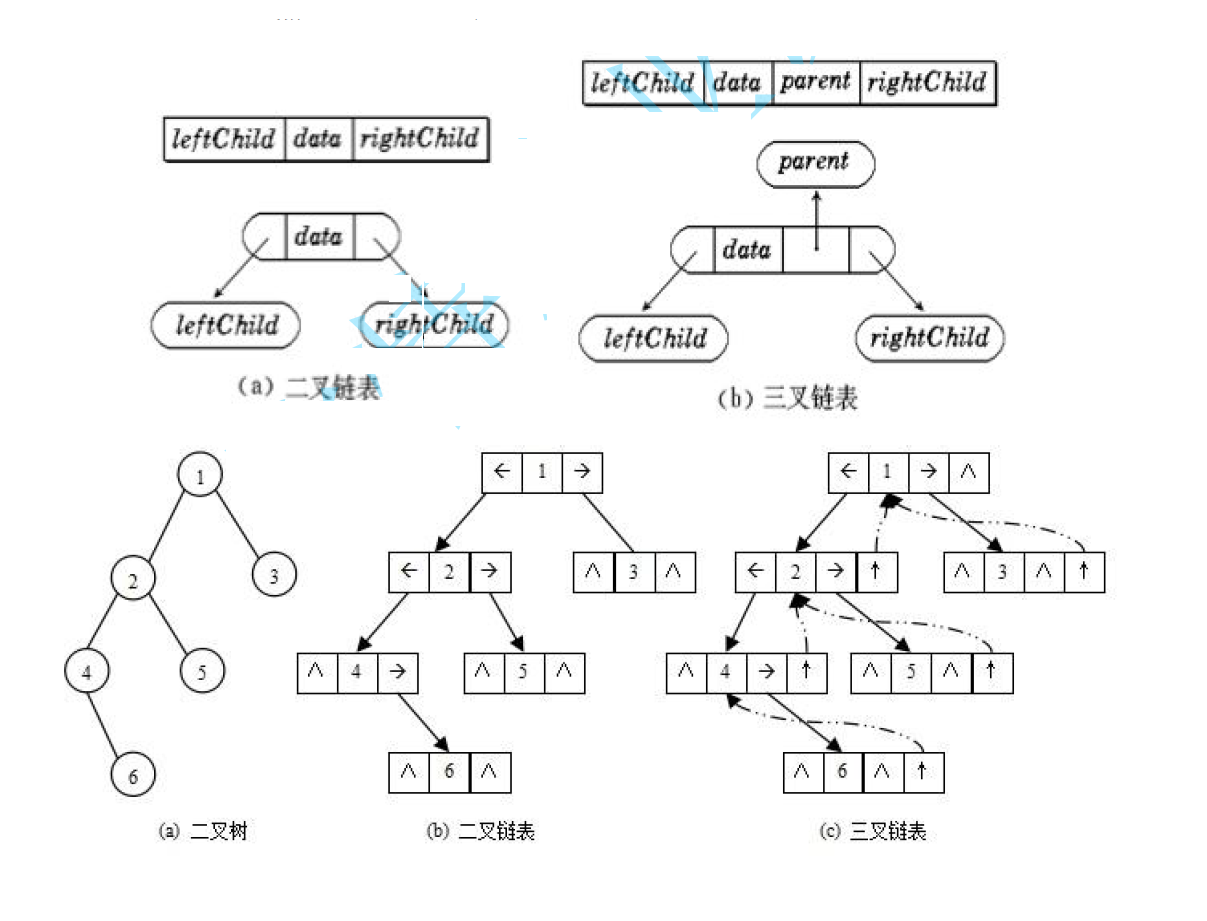
初识二叉树一、树概念及结构1、树的概念2、树的相关概念3、树的表示4、树在实际中的运用(表示文件系统的目录树结构)二、二叉树概念及结构1、概念2、特殊的二叉树3、二叉树的性质4、二叉树的存储结构三、结语一、树概念及结构 1、树的概念 树是一种非线…...
)
RV1126笔记三十二:基于 FastDeploy 在 RV1126 上的部署示例(RV1126 上部署 YOLOv5 检测模型测试)
若该文为原创文章,转载请注明原文出处。 FastDeploy是一款全场景、易用灵活、极致高效的AI推理部署工具, 支持云边端部署。提供超过 🔥160+ Text,Vision, Speech和跨模态模型📦开箱即用的部署体验,并实现🔚端到端的推理性能优化。包括 物体检测、字符识别(OCR)、…...
JVM垃圾回收——G1垃圾收集器
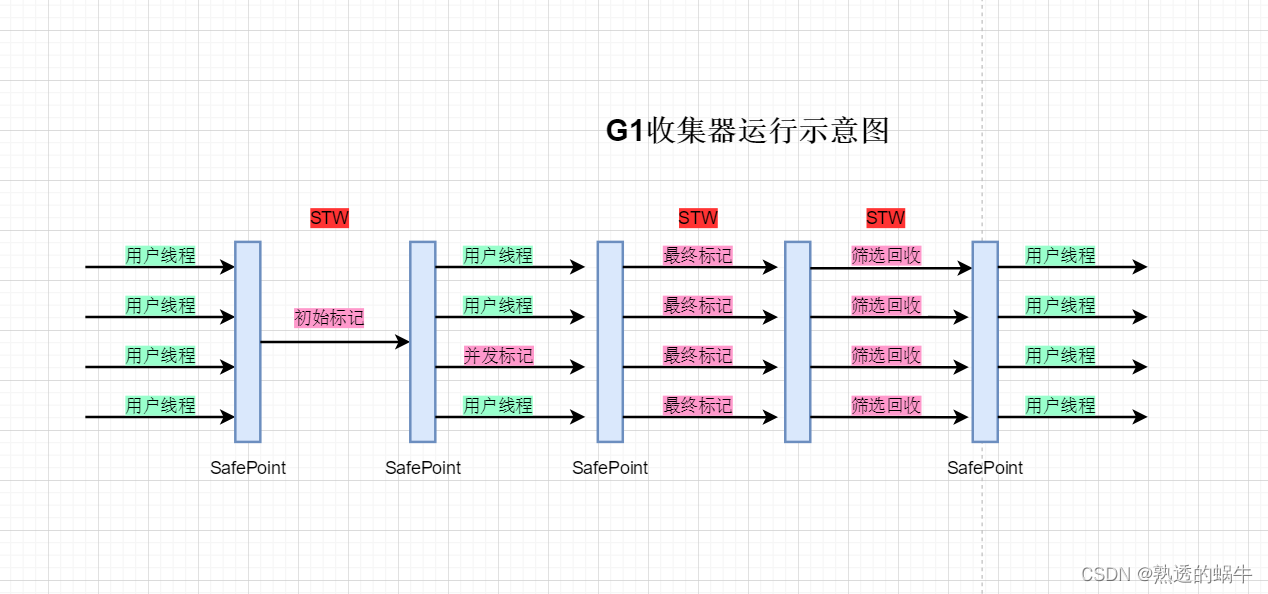
目录 一、什么是G1垃圾收集器 二、G1垃圾收集器的内存划分 三、G1垃圾收集器的收集过程 四、G1收集器的优缺点 五、G1收集器的JVM参数配置 一、什么是G1垃圾收集器 Garbage First(简称G1)收集器是垃圾收集器技术发展史上里程碑式的成果,它摒弃了传统垃圾收集器的…...
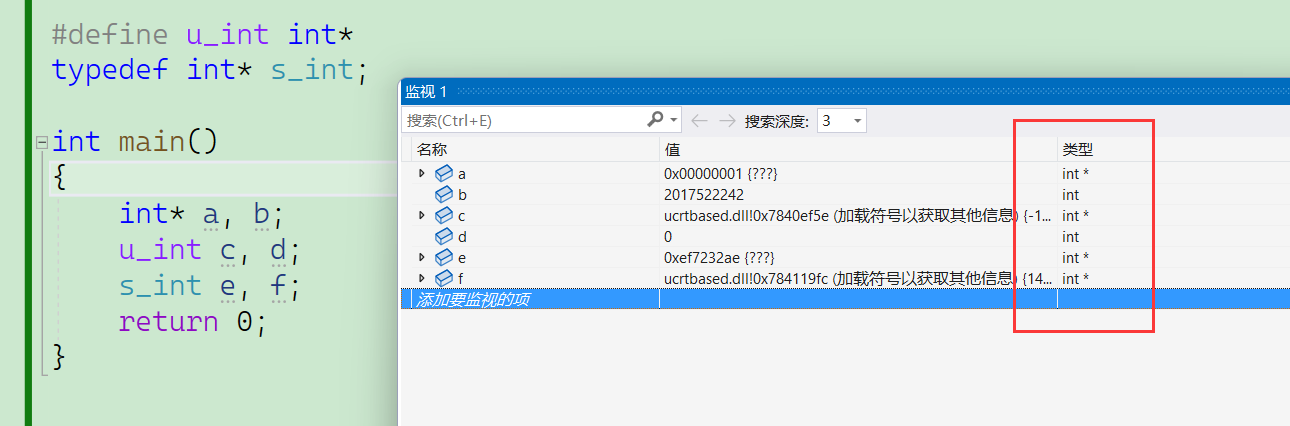
C语言深度剖析:关键字
C语言深度剖析:关键字C语言深度剖析:关键字前言定义与声明(补充内容)最宏大的关键字-auto最快的关键字-register关键字static被冤枉的关键字-sizeof整型在内存中的存储原码、反码、补码大小端补充理解变量内容的存储和取出为什么都是补码整型取值范围关于…...

聊一聊过度设计!
文章目录什么是过度设计?过度设计的坏处如何避免过度设计充分理解问题本身保持简单小步快跑征求其他人的意见总结新手程序员在做设计时,因为缺乏经验,很容易写出欠设计的代码,但有一些经验的程序员,尤其是在刚学习过设…...

程序员在小公司(没有大牛,人少)怎么成长?
大多数小公司都是创业公司,所以它们有着非常独特的“创业心态”。所谓创业心态通常表现为关注快速增长,竭尽所能让公司盈利,或者达成其他一些迫切目标。 在这样一家公司工作的软件开发人员,你极有可能要身兼多职,不能…...
【Fastdfs实战】在本地如何将文件上传到Linux虚拟机
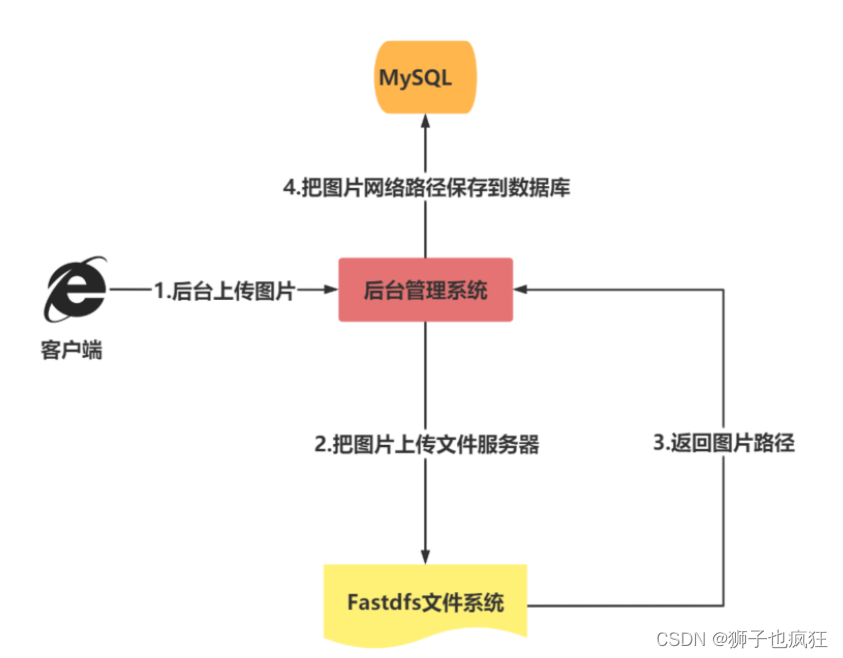
作者:狮子也疯狂 专栏:《Fastdfs连续剧》 坚持做好每一步,幸运之神自然会驾凌在你的身上 目录一. 🦁 前言二. 🦁 上传原理Ⅰ. 🐇 原理图解Ⅱ. 🐇 传输原理三. 🦁 实战演示Ⅰ. &…...

ERP 系统的应用对企业财务会计信息系统内部控制的影响
(一)对企业的财务信息数据进行实时和动态管理传统的财务会计信息系统一般都是采用单一的软件系统,所以在信息的传递及处理上常常不能满足企业的需要,信息与其他部门存在不对称及滞后的现象。而ERP 系统是通过有效的技术手段将企业的各种分散的数据进行完…...

智慧物联网源码带手机端源码 物联网系统源码
在智慧工厂领域,智慧城市领域,都需要对设备进行监控。比如工厂需要对周围环境温度、湿度、气压、电压,灯的开关进行监控。这时候就需要物联网平台来进行管理。 推荐一个基于java开发的物联网平台,前端HTML带云组态、可接入视频监…...

AI绘画进军三次元,有人用它打造赛博女友?(diffusion)
目录0 写在前面1 AI绘画技术飞跃2 效果展示3 环境配置3.1 下载基础模型3.2 更新.NET和模型3.3 下载绘画模型3.4 启动项目3.5 标签配置4 结语0 写在前面 机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理&a…...
计算机网络高频知识点
目录 一、http状态码 二、浏览器怎么数据缓存 三、强缓存与协商缓存 1、强缓存 2、协商缓存 四、简单请求与复杂请求 五、PUT 请求类型 六、GET请求类型 七、GET 和 POST 的区别 八、跨域 1、什么时候会跨域 2、解决方式 九、计算机网络的七层协议与五层协议分别指…...

谈谈前端性能优化-面试版
前言 当我们去面试的时候,很大概率会被面试官问这么一个问题:你有尝试过对项目做性能优化吗?或者你了解哪些性能优化的方法?听到这个问题的你可能是这样的: 似曾相识但又说不清楚,往往只能零散地说出那么几…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
