基于晶体结构算法的无人机航迹规划-附代码
基于晶体结构算法的无人机航迹规划
文章目录
- 基于晶体结构算法的无人机航迹规划
- 1.晶体结构搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用晶体结构算法来优化无人机航迹规划。
1.晶体结构搜索算法
晶体结构算法原理请参考:https://blog.csdn.net/u011835903/article/details/122851304
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得晶体结构搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用晶体结构算法对航迹评价函数式(7)进行优化。优化结果如下:

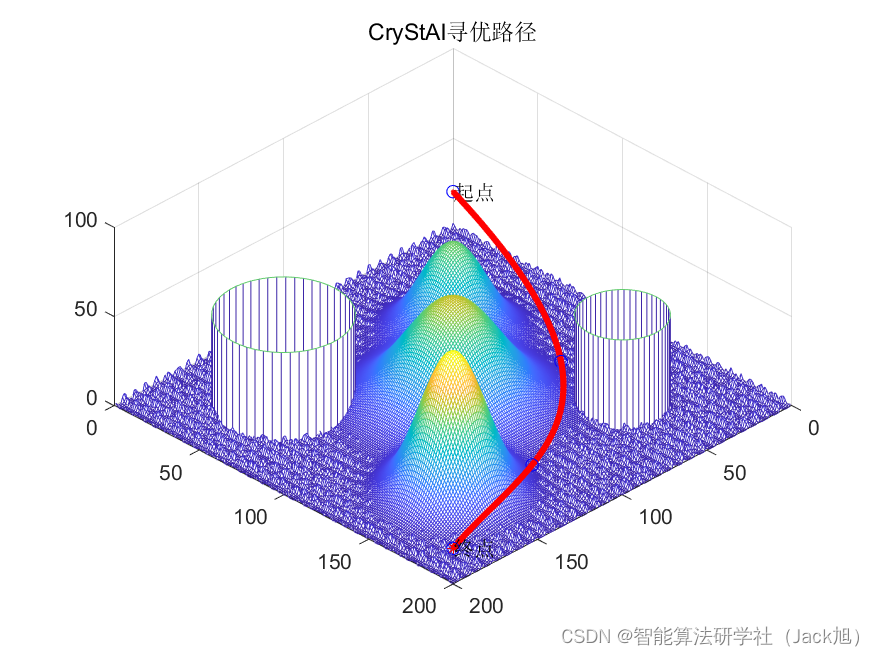
从结果来看,晶体结构算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于晶体结构算法的无人机航迹规划-附代码
基于晶体结构算法的无人机航迹规划 文章目录 基于晶体结构算法的无人机航迹规划1.晶体结构搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用晶体结构算法来优化无人机航迹规划。 …...

刷题笔记day11-栈与队列2
20. 有效的括号 这个是典型的使用栈,来进行匹配。 因为栈是先进后出,所以,最近的左括号一定在栈顶。如果不是,则就是不匹配了。 func isValid(s string) bool {stack : Stack{}dict : map[byte]byte {): (,]: [,}: {,}for _, it…...

ngixn的指令
Nginx是一个高性能的HTTP和反向代理服务器,它可以处理静态资源、动态内容、负载均衡、反向代理和HTTP缓存等任务。本文将详细介绍在CentOS上安装和配置Nginx服务器,并讲解Nginx常用指令。 安装Nginx 在CentOS上安装Nginx非常简单,只需要执行…...

管理类联考——数学——汇总篇——知识点突破——代数——函数、方程——记忆
文章目录 考点记忆/考点汇总——按大纲 整体局部 本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多,通常…...

2014年亚太杯APMCM数学建模大赛C题公共基础课教师专业化培养方式研究求解全过程文档及程序
2014年亚太杯APMCM数学建模大赛 C题 公共基础课教师专业化培养方式研究 原题再现 近年来,世界基础工业、信息产业、服务业的跨越式发展引发了大量人才需求,导致了职业教育的飞速发展,除原有专科层次高等职业教育院校外,大量普通…...

【广州华锐互动】VR历史古城复原:沉浸式体验古代建筑,感受千年风华!
在科技日新月异的今天,虚拟现实(VR)技术已经成为了我们生活中不可或缺的一部分。从娱乐游戏到医疗健康,从教育培训到房地产销售,VR技术的应用领域日益广泛。而近年来,VR技术在文化遗产保护和古迹复原方面的…...

http和https分别是什么?
HTTP(Hypertext Transfer Protocol)和HTTPS(HTTP Secure)是互联网上应用最为广泛的两类协议,都是用于在网络中进行数据交换。 1.HTTP: HTTP是一种无状态的协议,即服务器并不保持与客户端的连接…...
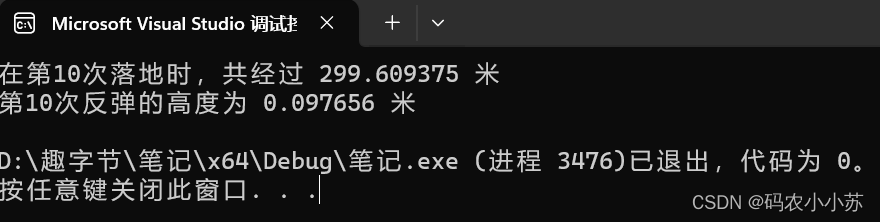
C语言--一个球从100m高度自由落下,每次落地后反弹回原高度的一半,再落下,再反弹。求它在第10次落地时共经过多少米,第10次反弹多高
一.思路分析 这是一个简单的物理题目,解题思路比较明确。程序使用 for 循环来模拟球的下落和反弹过程,通过多次计算得到最终结果,最后使用 printf 函数将结果输出。 定义初始高度 height 和总共经过的米数 distance 的变量,初始化…...

基础知识:位运算
基础知识:位运算 1. 两类表达式2. 项目中用到位运算的🌰 1. 两类表达式 2. 项目中用到位运算的🌰 在一个表中增加一个字段,控制报餐的6个字段包括午餐、晚餐、夜餐1、夜餐2、白班、晚班。正常在表中需要增加6个字段来做开关&…...

Android菜单Menu详解
菜单资源文件通常放置在res\menu目录下,在创建项目时,默认不自动创建menu目录,所以需手动创建。 Android Resource Directory→ value menu 或在创建根元素为<menu></menu>标记的xml文件对自动气建眼 res→Android Resounce File…...
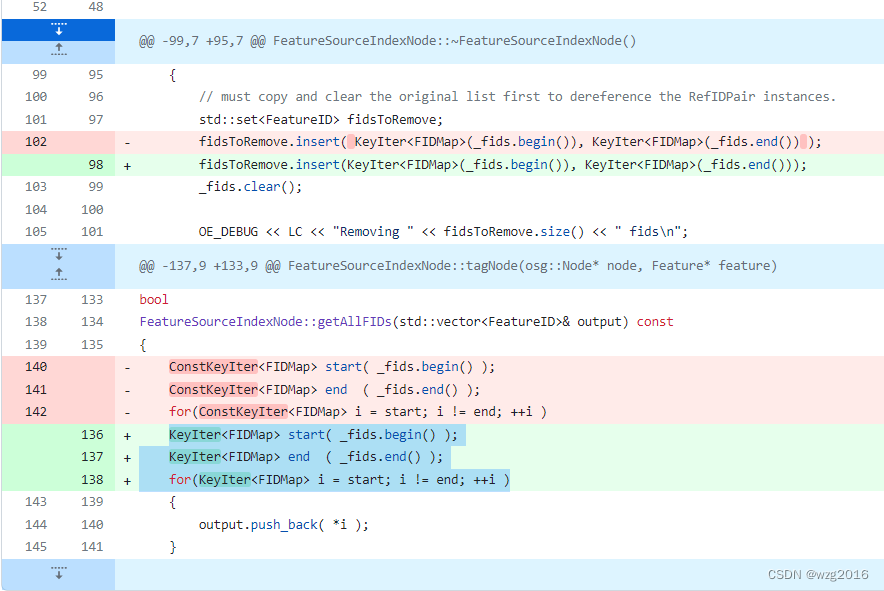
win10 + cmake3.17 + vs2017编译osgearth2.7.0遇到的坑
坑1:debug模式下生成osgEarthAnnotation时 错误:xmemory0(881): error C2440: “初始化”: 无法从“std::pair<const _Kty,_Ty>”转换为 to _Objty 出错位置:src/osgEarthFeatures/FeatureSourceIndexNode.cpp 解决办法: …...
 】.md updata:23/11/05)
【Linux网络编程_TCP/UDP_字节序_套接字 实现: FTP 项目_局域网聊天项目 (已开源) 】.md updata:23/11/05
文章目录 TCP/UDP对比端口号作用字节序字节序转换api套接字 socket实现网络通讯服务端 逻辑思路demo: 满血版双方通讯/残血版多方通讯 (配合进程实现)服务端 demo客户端 demo FTP 项目实现sever demo:client demo: 局域网多方通讯 ࿰…...

SpringBoot日志基础
1.yml 说明:配置yml文件。debug、info、warn、error。 logging:level:root: debug2.指定某个包 logging:level:root: info # 设置某个包的日志级别com.forever.controller: debug 3.分组调试 logging:# 设置分组group:ebank: com.forever.controlleriservic…...

linux文章导航栏
linux文章导航栏 问价解压缩大全Linux tar 备忘清单zip文件解压缩命令全 ubuntuubuntu18.04安装教程\搜狗输入法\网络配置教程Linux静态库和动态库 shellShell脚本命令...
Adobe:受益于人工智能,必被人工智能反噬
来源:猛兽财经 作者:猛兽财经 总结: (1)Adobe(ADBE)受益于生成式人工智能的兴起,其一直能实现两位数的收入增长就证明了这一点。 (2)在生成式人工智能兴起时,该公司就快…...
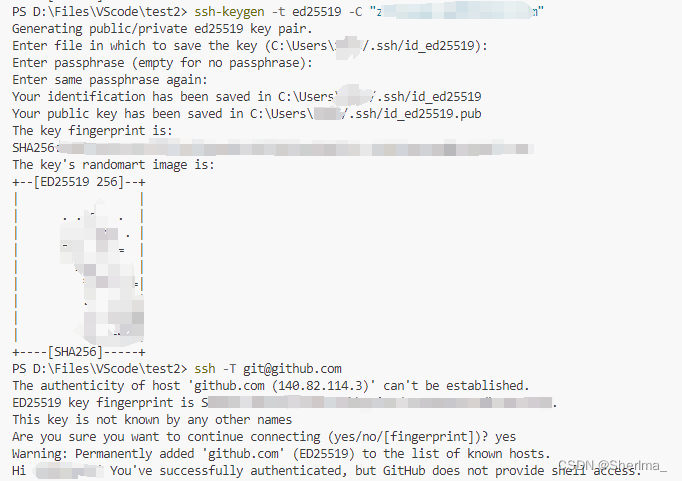
VScode配置 github 上传代码
初始化,设置用户名和密码 # 设置你的 Git 用户名 git config --global user.name author# 设置你的 Git 邮箱 git config --global user.email authorgmail.com# 确保 Git 输出带有颜色 git config --global color.ui auto# 查看 Git 配置 git list1. 初始化本地…...
)
mysql根据条件导出表数据(`--where=“文本“`)
本文只讲导出,导入可以参考不同MySQL服务的表以及库的数据迁移(/备份)-CSDN博客 现在先查下migration_one.table_11里有什么: SELECT * FROM migration_one.table_11;id name ------ -------- 12321 hehe 1321 …...
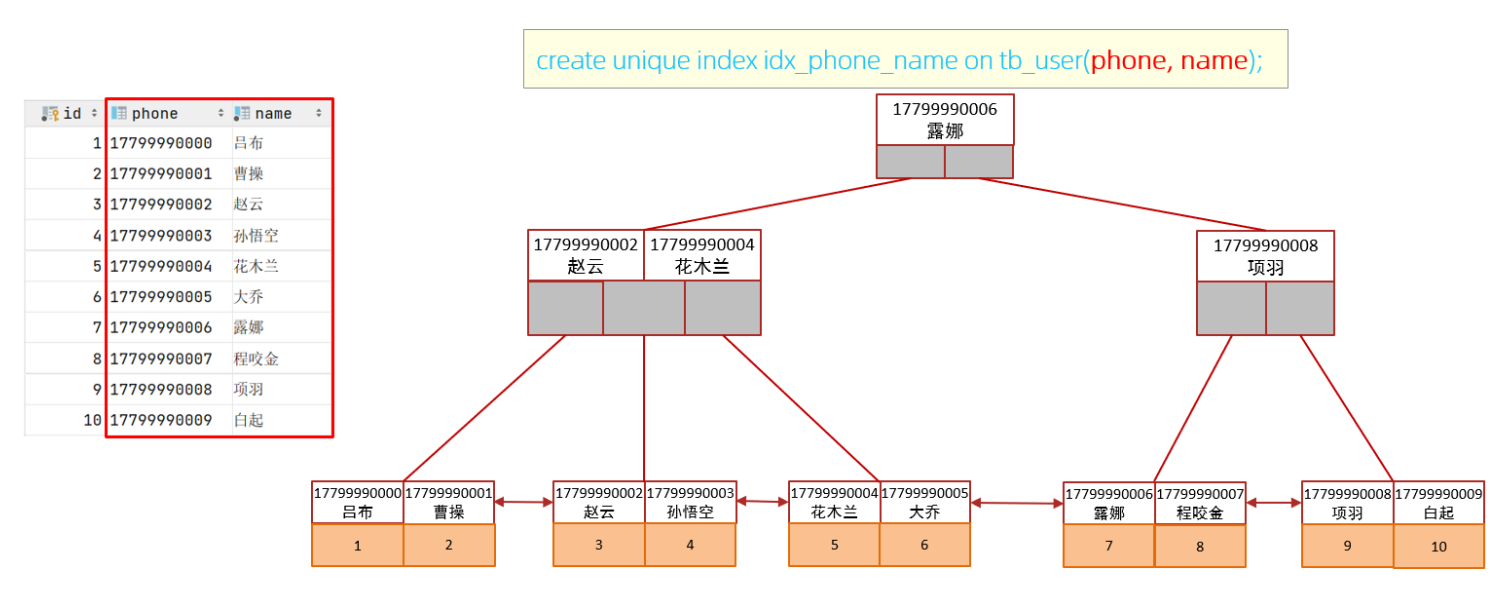
MySQL复习总结(二):进阶篇(索引)
文章目录 一、存储引擎1.1 MySQL体系结构1.2 存储引擎介绍1.3 存储引擎特点1.4 存储引擎选择 二、索引2.1 基本介绍2.2 索引结构2.3 索引分类2.4 索引语法2.5 SQL性能分析2.6 索引使用2.6.1 最左前缀法则2.6.2 范围查询2.6.3 索引失效情况2.6.4 SQL提示2.6.5 覆盖索引2.6.6 前缀…...
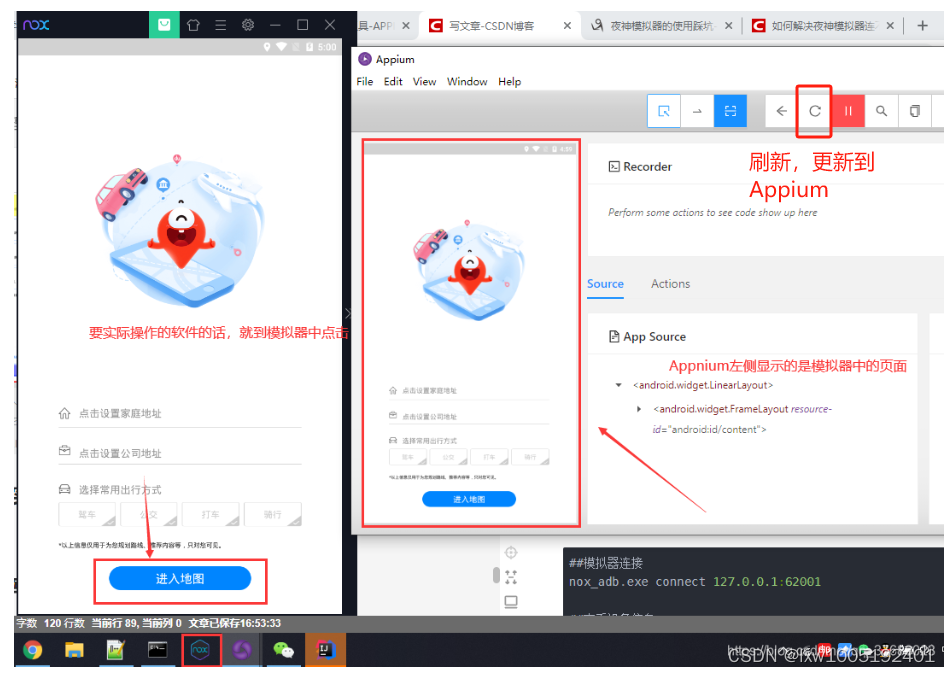
java APP自动化测试AppIum
一、前言 二、Appium环境搭建 2.1 JDK安装 2.2 Android SDK安装配置 2.3 模拟器安装及配置 2.4 Appium Desktop安装及使用 2.5 Appium配置连接模拟器 三、实战基本脚本编写 3.1 创建Maven项目并配置 3.2 简单Demo 四、写在最后 一、前言 随着移动互联网的发展,AP…...
)
【洛谷 P1303】A*B Problem 题解(高精度+字符串)
A*B Problem 题目描述 给出两个非负整数,求它们的乘积。 输入格式 输入共两行,每行一个非负整数。 输出格式 输出一个非负整数表示乘积。 样例 #1 样例输入 #1 1 2样例输出 #1 2提示 每个非负整数不超过 1 0 2000 10^{2000} 102000。 思路 …...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
