算法通过村第十八关-回溯|青铜笔记|什么叫回溯(中篇)
文章目录
- 前言
- 回溯的核心问题
- 撤销操作解释
- 总结
前言
提示:阳光好的时候,会感觉还可以活很久,甚至可以活出喜悦。 --余秀华
回溯是非常重要的算法思想之一,主要解决一些暴力枚举也搞不定的问题(这里埋个坑💣)例如组合、分割、子集、棋盘等等。从性能角度来看回溯算法的效率并不是很高,但是对于暴力也解决不了的问题,它往往很快可以出结果,效率低就可以理解了吧。接下来,就看看回溯的事情吧🤩
回溯的核心问题
递归+局部枚举+放下前任
接着看这个题目:77. 组合 - 力扣(LeetCode)

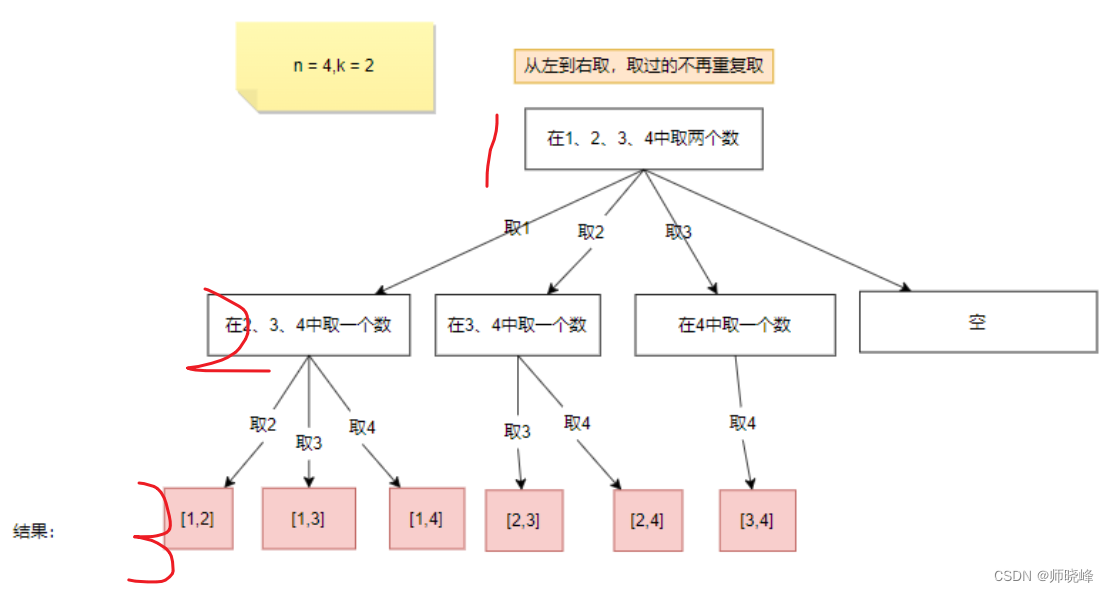
当n = 4时,我们可以选择的有n有{1,2,3,4}这四种情况,所以我们从第一层到第二层的分支有四个,分别表示可取1,2,3,4.而且这里从左到右取数,取过的数,不在重复取。第一次取1,集合变为2,3,4.因为k= 2,我们也只能再取1个数就可以了,分别取2,3,4.得到的集合就是[1,2]、[1,3]、[1,4]。一次类推:
横向:
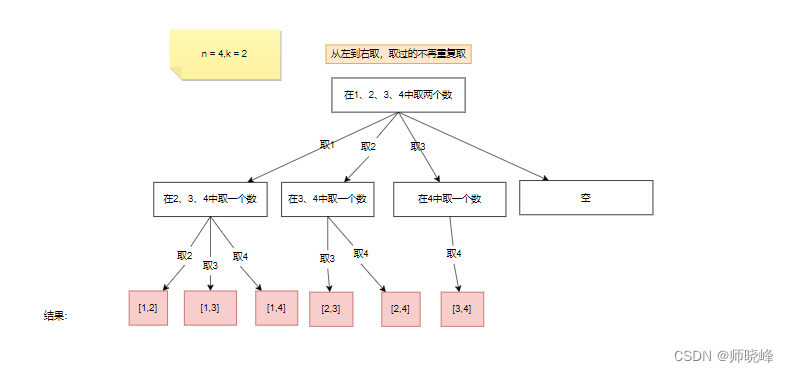
每次从集合中选取元素,可选择的范围回逐步收缩,到了取4时就直接返为空了。
继续观察树结构,可以发现,图中每次访问到一个叶子节点(图中的标记处),我们就可以得到一个结果。虽然到最后时空的,但是不影响最终结果。这里相当于从根节点开始每次选择的内容(分支)达到叶子节点时,将其收起起来就是我们想要的结果。
你可以尝试画下n=5,k=3的结果:有没有感觉
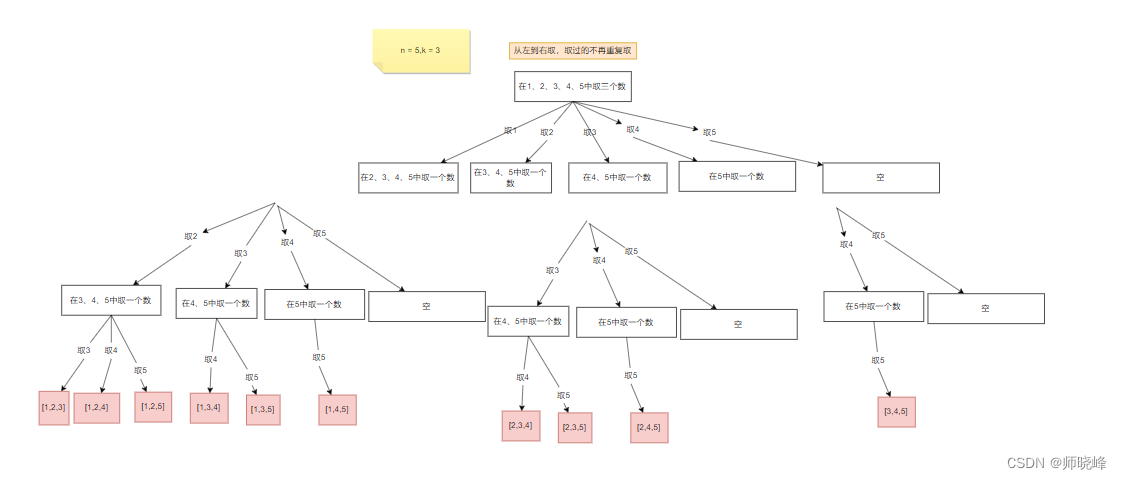
从图中我们发现元素个数n相当于树的宽度(横向),而每个结果的元素个数k相当于树的深度(纵向)。所以我们说回溯问题就是一纵一横而已。在分析我们回发现下面几个规律:
- 我们每次选择都是从类似{1,2,3,4},{1,2,3,4}这个样的序列中一个一个选的,这就是为什么说是局部枚举,后面的枚举范围回越来越小。
- 枚举时,我们就是简单的暴露测试而已,一个一个验证,能否满足要求,从上图可以看到,这就是N叉树的遍历过程,一次代码相似度很高。
- 我们再看叶子过程,这部分是不是和(n = 4,k = 2)处理的结果一致,也就说是很明显的递归结构。
到此,我们还有一个问题待解决,就是回溯一般会有一个手动撤销的操作,为什么要这么做呢?
继续观察纵横图:
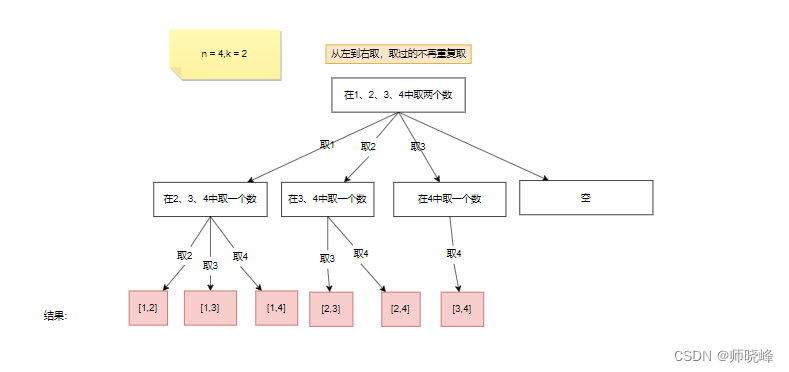
我们可以看到,我们收集的每个结果不是针对叶子节点的,而是针对树枝的,比如最上层我们首先确定了1,下层我们如果选择了2,那么结果就是{1,2},如果选择了3,结果就是{1,3}.一次类推。现在时怎么确定得到第一个结果时{1,2}之后,得到第二个结果是{1,3}呢?
继续观察纵横图 ,可以看到,我们在得到{1,2}之后将2撤销,再继续使用3,就得到了{1,3},同理也可以得到{1,4},之后这一层就没有了,我们可以撤销1,继续从最上层取2继续进行。
这里对应的代码操作就是先将第一个结果放在临时列表的Path里面,得到第一个结果{1,2},之后就将path里面的内容放进结果列表resultList中,之后,将path里面的2撤销掉,继续寻找下一个结果{1,3},继续将path加入resultList中,然后再次撤销,继续寻找。
现在了解为什么要撤销,看图。这个过程,我们称它“放下前任,继续前进”,后面的回溯大都是这样的思路。
这几条就是回溯的基本规律,了解这一点,我们就可以看看代码是怎么回事了,到此我们看看完整的代码时怎样的:
public List<List<Integer>> combine(int n, int k) {List<List<Integer>> res = new ArrayList<>();if (k <=0 || n < k){return res;}
Deque<Integer> path = new ArrayDeque<>();
dfs(n,k,1,path,res);return res;}
public void dfs(int n,int k,int startIndex,Deque<Integer> path,List<List<Integer>> res){// 递归终止条件,path 等于k(刚好完成一次if (path.size() == k){res.add((new ArrayList<>(path)));return;}// 针对每个节点,这里就是遍历搜索,也就是枚举for(int i = startIndex; i <= n; i++){// 向路径里添加一个数(分支里的取值path.addLast(i);// 搜索起点要加1,就是缩小范围,准备下一轮递归(这里不允许重复dfs(n,k,i + 1,path,res);// 递归之后要做同样的逆向操作,撤销掉path.removeLast();}}
上面代码还有一个问题需要解释:startIndex和i是怎么变化的,为什么要传递到下一层(+ 1)
我们来看看这里的递归循环:
// 针对每个节点,这里就是遍历搜索,也就是枚举for(int i = startIndex; i <= n; i++){// 向路径里添加一个数(分支里的取值path.addLast(i);// 搜索起点要加1,就是缩小范围,准备下一轮递归(这里不允许重复dfs(n,k,i + 1,path,res);// 递归之后要做同样的逆向操作,撤销掉path.removeLast();}
这里的循环有什么作用呢?看看这里,其实来说是一个枚举,第一次n=4,可以选择1,2,3,4四种情况,所以就存在4个分支,for就需要执行4次:
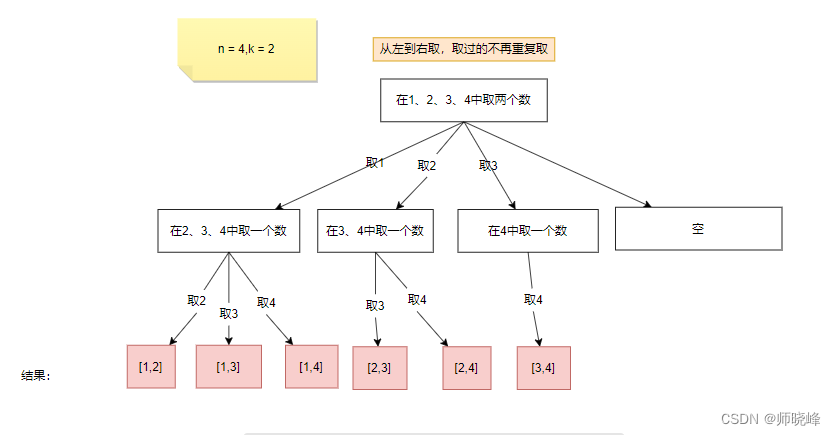
对于第二层来说,第一个数,选择1之后,身下的元素就只有2,3,4了。所以这时候for循环就执行3次,后面的只有2次和1次了。
撤销操作解释
如果你还是不清楚的话,这里就带图详细的走一遍,回溯也就是这个地方有点晕,拿下就是胜利✌。
// 针对每个节点,这里就是遍历搜索,也就是枚举for(int i = startIndex; i <= n; i++){// 向路径里添加一个数(分支里的取值path.addLast(i);// 搜索起点要加1,就是缩小范围,准备下一轮递归(这里不允许重复dfs(n,k,i + 1,path,res);// 递归之后要做同样的逆向操作,撤销掉path.removeLast();}
为什么要remove呢?看下图,当第一层取1时,最底层的遍历从左到右执行,取2,取3,取4.而取3的时候,此时res里面存储的是{1,2},所以这里前提是需要撤销掉2(path.removeLast();)的作用。
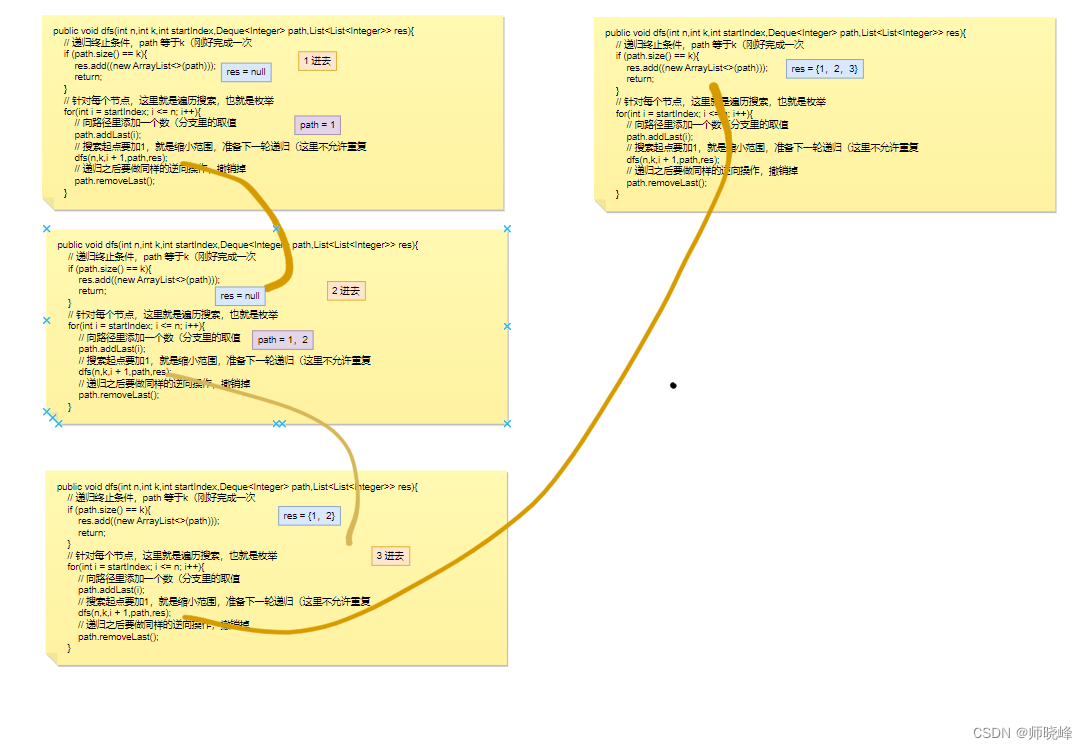
这里我们拆解一下递归方法,将递归拆分成函数调用,输出第一条路径{1,2}的步骤如下:
我们在递归说过一个特点:不到南墙不回头,回溯也是这个道理,我们看看这个过程。

然后,怎么在次进行呢,这里就需要撤回一下了,但是如果将这里的remove代码去掉,就会是这个样子:
这里知道遍历完成,然会的就不做撤销,就会下一场进入for循环,也就是回变成{1,2,3}.
path是一个全局的引用的,各个递归的函数是公用的,所以这里处理完{1,2},之后,需要把2撤出去,将1保留,再让三进入,从而得到{1,3}.所以这里不许remove一下的。
同样处理完之后,后续的也是依次处理,需要撤销的,这里也就是不得不处理撤销的操作。
总结
提示:什么叫回溯;保留状态;撤销操作;回溯核心思想;回溯的入门
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。

相关文章:

算法通过村第十八关-回溯|青铜笔记|什么叫回溯(中篇)
文章目录 前言回溯的核心问题撤销操作解释总结 前言 提示:阳光好的时候,会感觉还可以活很久,甚至可以活出喜悦。 --余秀华 回溯是非常重要的算法思想之一,主要解决一些暴力枚举也搞不定的问题(这里埋个坑💣…...
)
generate by chatgpt:应用上线前的checkList(部分是我自己的回答)
prompt 1 想象你是一名高级测试工程师,在应用上线前你需要提供一份checklist,请写出来: 作为一名高级测试工程师,以下是我在应用上线前的检查清单: 功能性测试: 检查所有要素和功能是否正常工作。确保满足了所有用户故事/需求。…...

Redis实战 | 使用Redis 的有序集合(Sorted Set)实现排行榜功能,和Spring Boot集成
专栏集锦,大佬们可以收藏以备不时之需 Spring Cloud实战专栏:https://blog.csdn.net/superdangbo/category_9270827.html Python 实战专栏:https://blog.csdn.net/superdangbo/category_9271194.html Logback 详解专栏:https:/…...
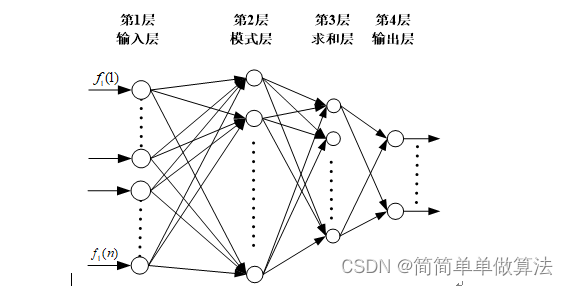
基于信号功率谱特征和GRNN广义回归神经网络的信号调制类型识别算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 MATLAB2022a 3.部分核心程序 ................................................................ %调制识别 len1 func_f…...

matplotlib从起点出发(10)_Tutorial_10_Layout
使用受约束的绘图干净整洁地将图形合适排列。 受约束的布局会自动调整子图,以便刻度标签、图例和颜色条等装饰不会重叠,同时仍保留用户请求的逻辑布局。 受约束布局类似于“紧密布局”,但它要更灵活。它处理放置在多个轴上的Axes(放置颜色条…...
(转载))
HTTP头部信息解释分析(详细整理)(转载)
这篇文章为大家介绍了HTTP头部信息,中英文对比分析,还是比较全面的,若大家在使用过程中遇到不了解的,可以适当参考下 HTTP 头部解释 1. Accept: 告诉WEB服务器自己接受什么介质类型,/ 表示任何类型&#…...
集线器、交换机、网桥、路由器、网关
目录 集线器(HUB)交换机(SWITCH)网桥(BRIDGE)路由器(ROUTER)网关(GATEWAY)交换机和路由器的区别参考 集线器(HUB) 功能 集线器对数据的传输起到同步、放大和整形的作用 属于物理层设备 工作机制 使用集线器互连而成的以太网被称为共享式以太网。当某个主机要给另一个主机发送单…...

项目实战:新增@Controller和@Service@Repository@Autowire四个注解
1、Controller package com.csdn.mymvc.annotation; import java.lang.annotation.*; Target(ElementType.TYPE) Retention(RetentionPolicy.RUNTIME) Inherited public interface Controller { }2、Service package com.csdn.mymvc.annotation; import java.lang.annotation.*…...

校验 ChatGPT 4.0 真实性的三个经典问题:快速区分 GPT3.5 与 GPT4,并提供免费测试网站
现在已经有很多 ChatGPT 的套壳网站,以下分享验明 GPT-4 真身的三个经典问题,帮助你快速区分套壳网站背后到底用的是 GPT-3.5 还是 GPT-4。 大家可以在这个网站测试:https://ai.hxkj.vip,免登录可以问三条,登录之后无限…...
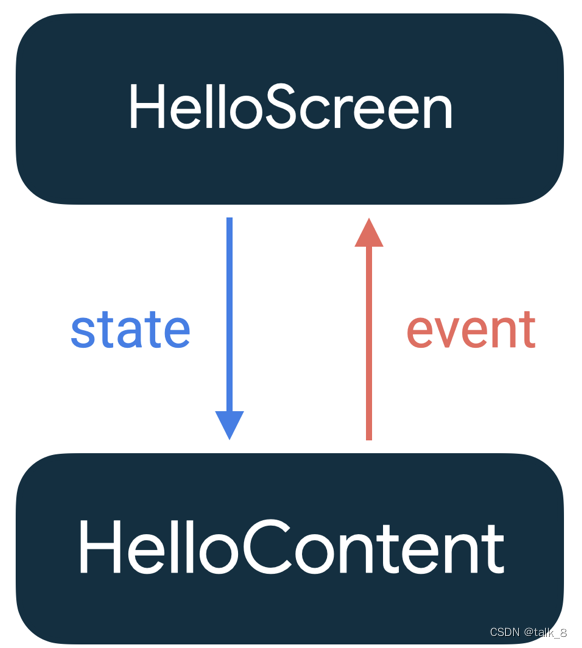
Jetpack:030-Jetpack中的状态
文章目录 1. 概念介绍2. 使用方法2.1 可监听对象2.2 获取状态值2.3 修改状态值2.4 重组函数 3. 示例代码4. 内容总结 我们在上一章回中介绍了Jetpack中网格布局相关的内容,本章回中主要 介绍状态。闲话休提,让我们一起Talk Android Jetpack吧࿰…...
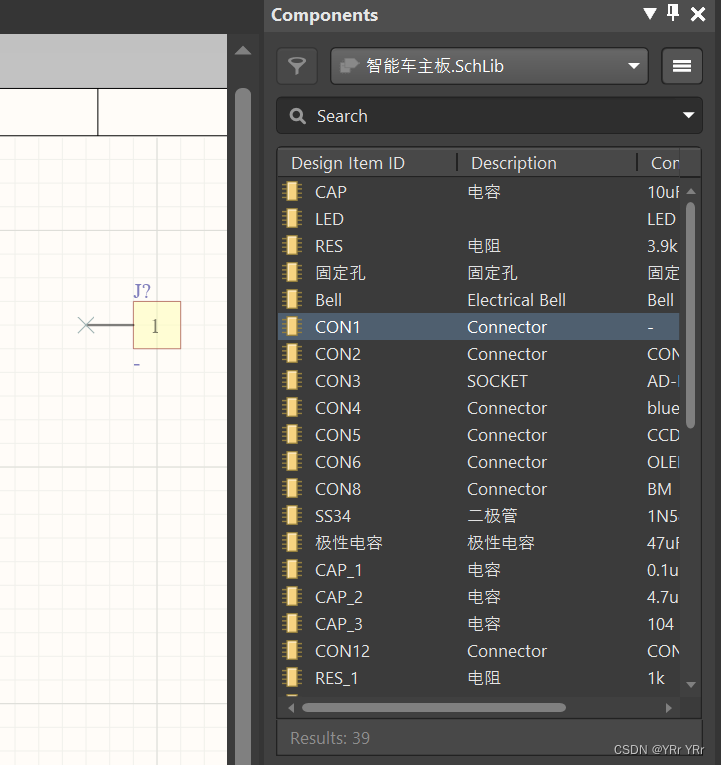
AD教程 (七)元件的放置
AD教程 (七)元件的放置 第一种放置方法 点击右下角Panels,选择SCH Library,调出原理图库器件列表选中想要放置的元件,点击放置,就会自动跳转到原理图,然后放置即可这种方法需要不断打开元件库…...

ubuntu22.04为什么鼠标会自动丢失焦点
排查的步骤 在Ubuntu 22.04中,鼠标自动丢失焦点可能由多种原因引起,包括系统错误、驱动问题、软件冲突或者某些特定的系统设置。以下是一些可能的原因和相应的解决方法: 触控板干扰: 如果你使用的是笔记本电脑,触控板可…...
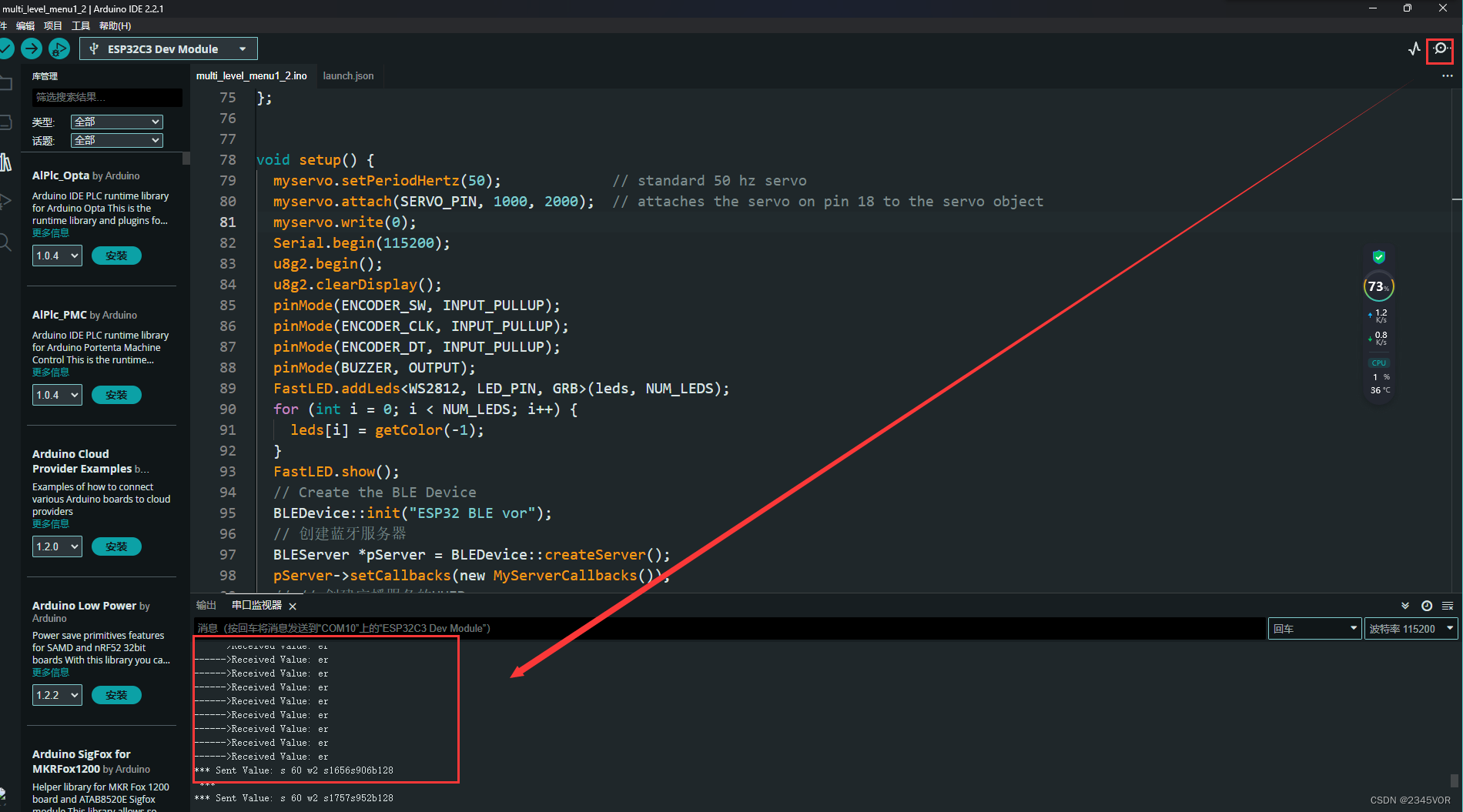
FastBond2阶段2——基于ESP32C3开发的简易IO调试设备
1. 项目介绍 之前买了许多国产单片机esp32c3一直在吃灰,没有发挥它的真实价值。非常感谢硬禾组织的Fastbond2活动,刚好两者经过微妙的碰撞。恰可以用于FastBond2活动主题4 - 测量仪器(单片机开发测试领域),或者用于国…...
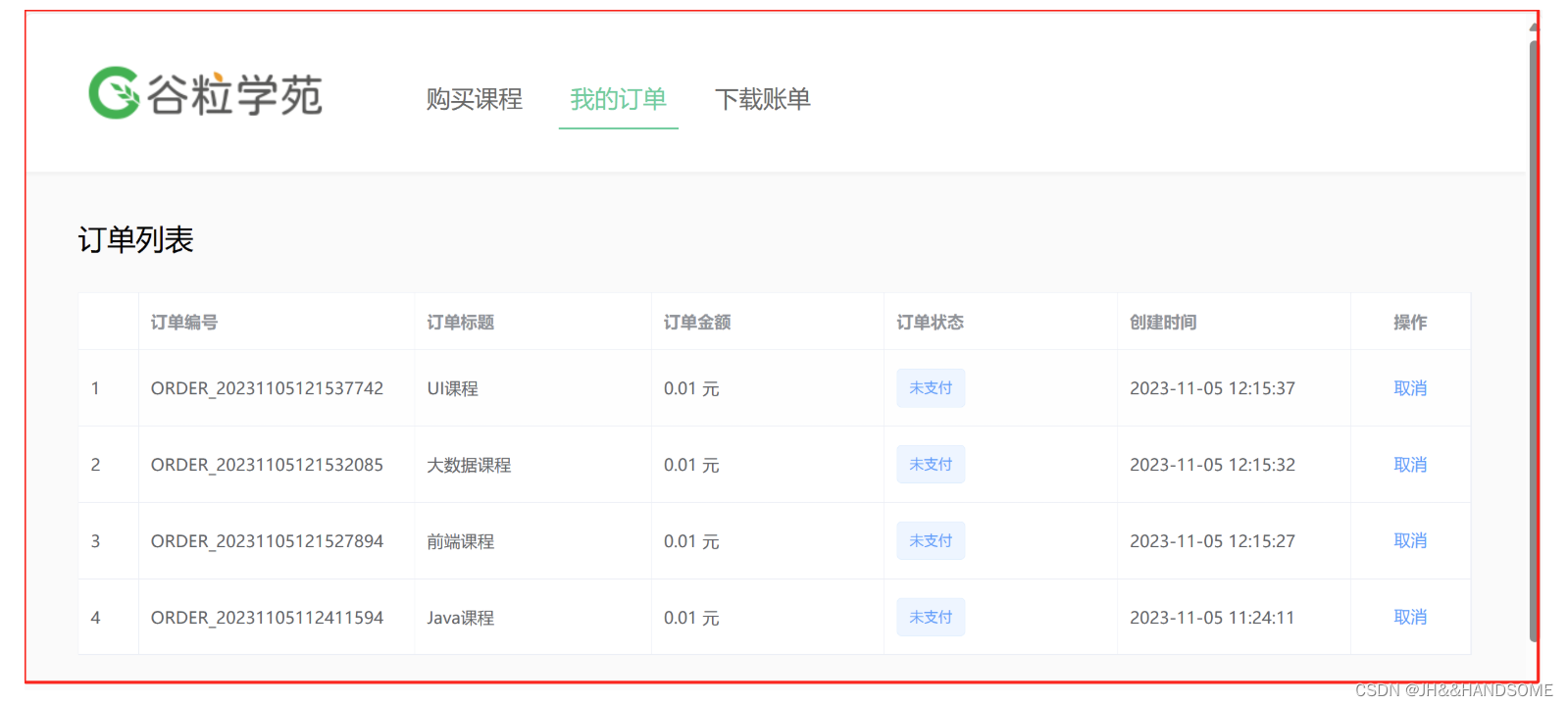
03、SpringBoot + 微信支付 ---- 创建订单、保存二维码url、显示订单列表
目录 Native 下单1、创建课程订单保存到数据库1-1:需求:1-2:代码:1-3:测试结果: 2、保存支付二维码的url2-1:需求:2-2:代码:2-3:测试:…...

【echarts基础】在柱形图上设置文本
一、需求描述 在柱状图上设置文本标签,按需修改它的颜色、大小、边框、阴影等,如下。 二、代码展示 series:[{name:"螺蛳粉",type:"bar",data:data.data.chartData.chartData.num.螺蛳粉,label:{//图形上显示文本标签formatter:&q…...

小户型工业风,陌生上开花知书香。福州中宅装饰,福州装修
漫步陌上 只因陌上花开 花是自然的那种 朴素而恬淡,不落尘俗。—徐志摩 小户型工业风格 满足业主需求 筑造书香押韵家 从动线、色彩、选材、定制等各个环节 与业主一起畅谈家的构造 形成别“居”一格的温暖品质家 以书做墙 告别电视墙 这是一个实用性很强的…...

Gorm 中的迁移指南
探索使用 GORM 在 Go 中进行数据库迁移和模式更改的世界 在应用程序开发的不断变化的景观中,数据库模式更改是不可避免的。GORM,强大的 Go 对象关系映射库,通过迁移提供了一种无缝的解决方案来管理这些变化。本文将作为您全面的指南…...
基于.NET、Uni-App开发支持多平台的小程序商城系统 - CoreShop
前言 小程序商城系统是当前备受追捧的开发领域,它可以为用户提供一个更加便捷、流畅、直观的购物体验,无需下载和安装,随时随地轻松使用。今天给大家推荐一个基于.NET、Uni-App开发支持多平台的小程序商城系统(该商城系统完整开源…...
)
[python] 在多线程中将`logging.info`输出到不同的文件中 (生产者消费者)
在多线程中将logging.info输出到不同的文件中,可以使用Python标准库中的Queue和Thread模块。具体实现步骤如下: 创建多个Queue队列用于不同线程的日志输出,每个队列对应一个日志文件。 import queue# 创建三个队列用于不同线程的日志输出 l…...

MySQL进阶_5.逻辑架构和SQL执行流程
文章目录 第一节、逻辑架构剖析1.1、服务器处理客户端请求1.2、Connectors1.3、第1层:连接层1.4、第2层:服务层1.5、 第3层:引擎层1.6、 存储层1.7、小结 第二节、SQL执行流程2.1、查询缓存2.2、解析器2.3、优化器2.4、执行器 第三节、数据库…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
