苹果加大对印度的扶持,提高在其生产iphone的比重
KlipC报道:跟踪苹果产业链,有分析师预计2023年全球约12%-14%的iphone在印度生产,预计2024年,印度将生产20%-25%的iphone。
KlipC的合伙人Andi D表示:“近年来随着苹果对中国的以来,印度已经成为高科技制造和组装的热门地区。”

D先生指出印度在今年第二季度首次超过了法国以及德国,成为iphone的第五大市场,尽管苹果在智能手机市场的份额不高,但苹果CEO库克也将其视为潜在增长地区。
值得一提的是,2023年财年,苹果在印度的营收达500亿卢比,销售额增长48%,达4932.1亿卢比,净利润达222.9亿卢比,同比上涨76%,而这也是苹果在印度过去5年里净利润增长最快的一次。
随着苹果正在加大地印度的投资,生产和研发的重心向印度转移,据悉苹果还计划让印度参与到新款iphone的研发中,这将是苹果首次在中国以外地区研发的新款的iphone,选择标准版iPhone 的主要原因是设计开发难度较低,可以降低风险。

这一举措可强化苹果与印度政府的合作关系,有利于未来在印度市场销售iPhone与其他产品,并且可能会成为他们未来十年发展中的关键市场。
高盛分析师指出,近年来,随着苹果逐渐减少对中国的依赖,印度很可能会成为最大的iphone制造国。
KlipC的机构会员Alex Su表示:“对于苹果来说,这些举措一方面是可以拓展印度快速发展的市场,一方面在印度生产iPhone可以在一定程度下降低生产成本。”
相关文章:

苹果加大对印度的扶持,提高在其生产iphone的比重
KlipC报道:跟踪苹果产业链,有分析师预计2023年全球约12%-14%的iphone在印度生产,预计2024年,印度将生产20%-25%的iphone。 KlipC的合伙人Andi D表示:“近年来随着苹果对中国的以来,印度已经成为高科技制造和…...
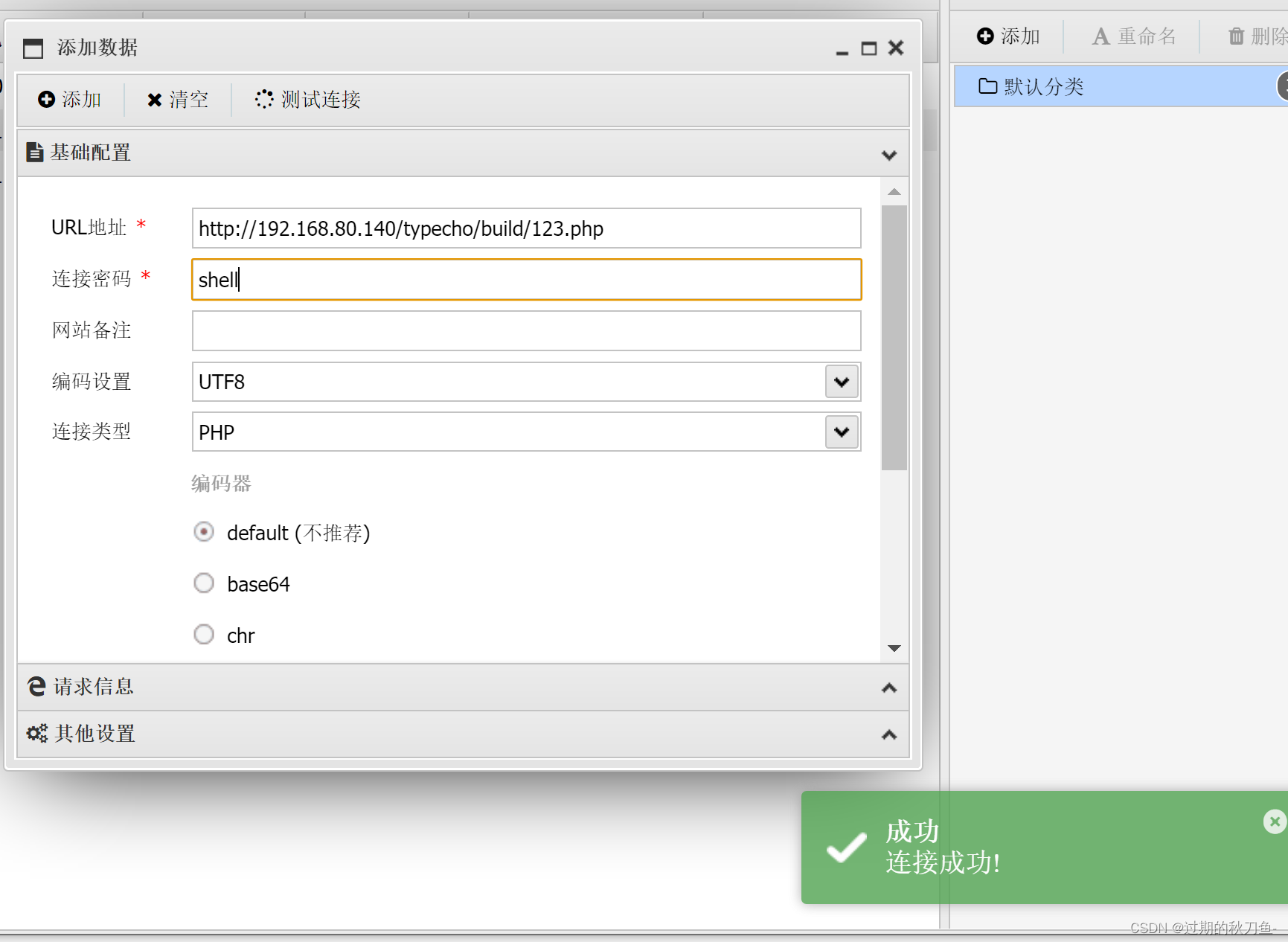
【漏洞复现】typecho_v1.0-14.10.10_unserialize
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 漏洞利用GetShell 下载链接:https://pan.baidu.com/s/1z0w7ret-uXHMuOZpGYDVlw 提取码:lt7a 首页 漏洞点:/install.php?finish 漏洞利用 …...

Linux常见面试题
1、 冯诺依曼体系的要点是: 数字计算机的数制采用二进制,bit 位, byte 字节 1 byte 8 bit计算机应该按照程序顺序执行计算机硬件由运算器、控制器、存储器、输入设备和输出设备五大部分组成 2、计算机的硬件五个组件 控制器: 指挥系统运算器: 数学和逻…...
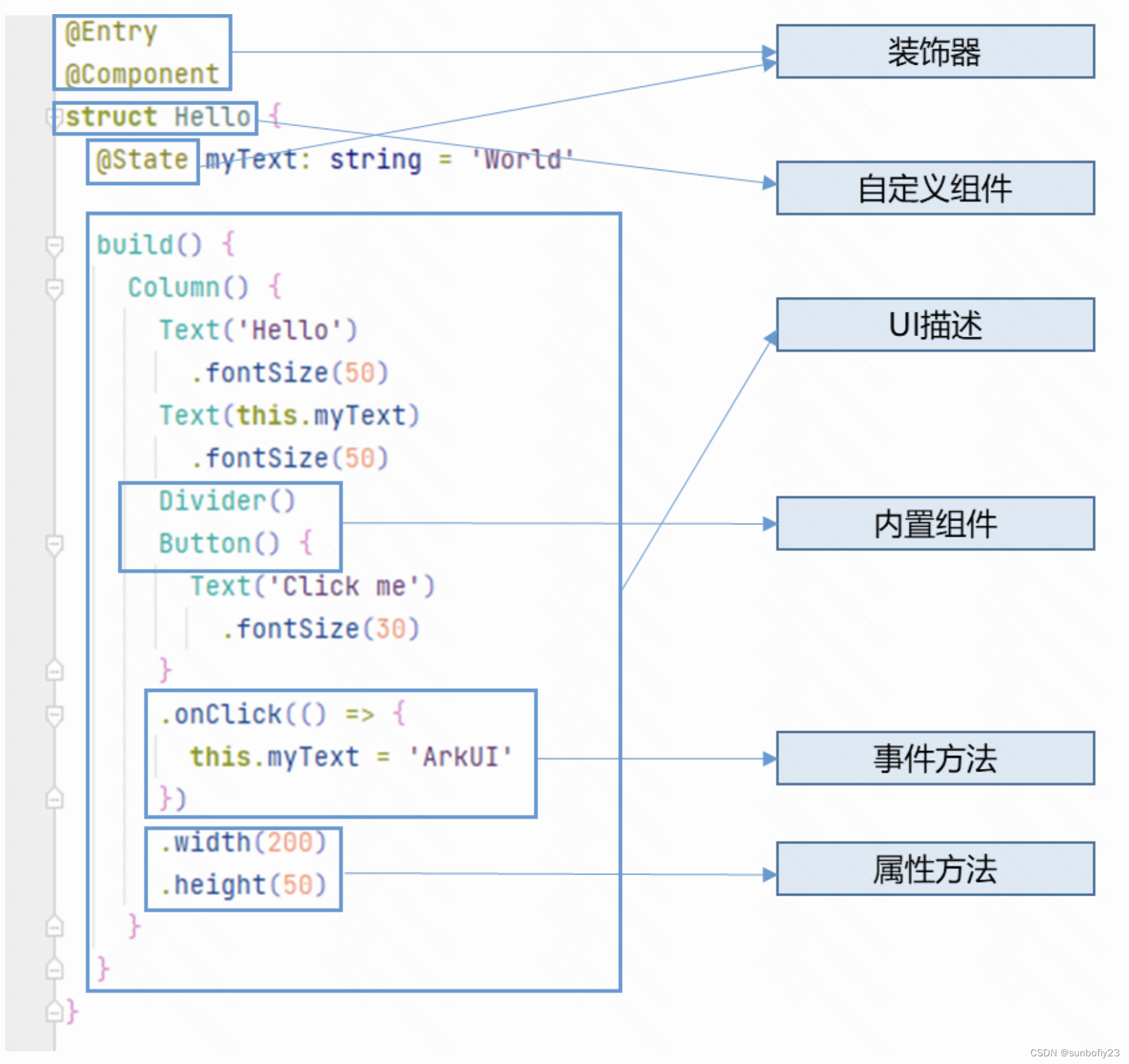
HarmonyOS ArkTS基础知识
概述 上一节,学习了TypeScript的基础语法,而在鸿蒙开发当中,有基于自己的编程语言,便是ArkTS。它是一种声明式UI的编程范式的语言,开发框架如下图所示: 根据框架图,分析,我将它大致…...

嵌入式课后习题第一章解答
嵌入式系统是一种以应用为中心,以计算机技术为基础,软/硬件可裁剪,适应应用系统对功能、可靠性、成本、体积、功耗严格要求的专用计算机。它与通用PC的区别主要体现在以下几个方面: 应用针对性:嵌入式系统是专为特定应…...
postMessage
A:端口3000 import React, { useEffect } from react;function App() {useEffect(() > {const childWindow document.getElementById(child).contentWindow;const sendMessageToChild () > {childWindow.postMessage("主页面消息", "http://localhost:…...
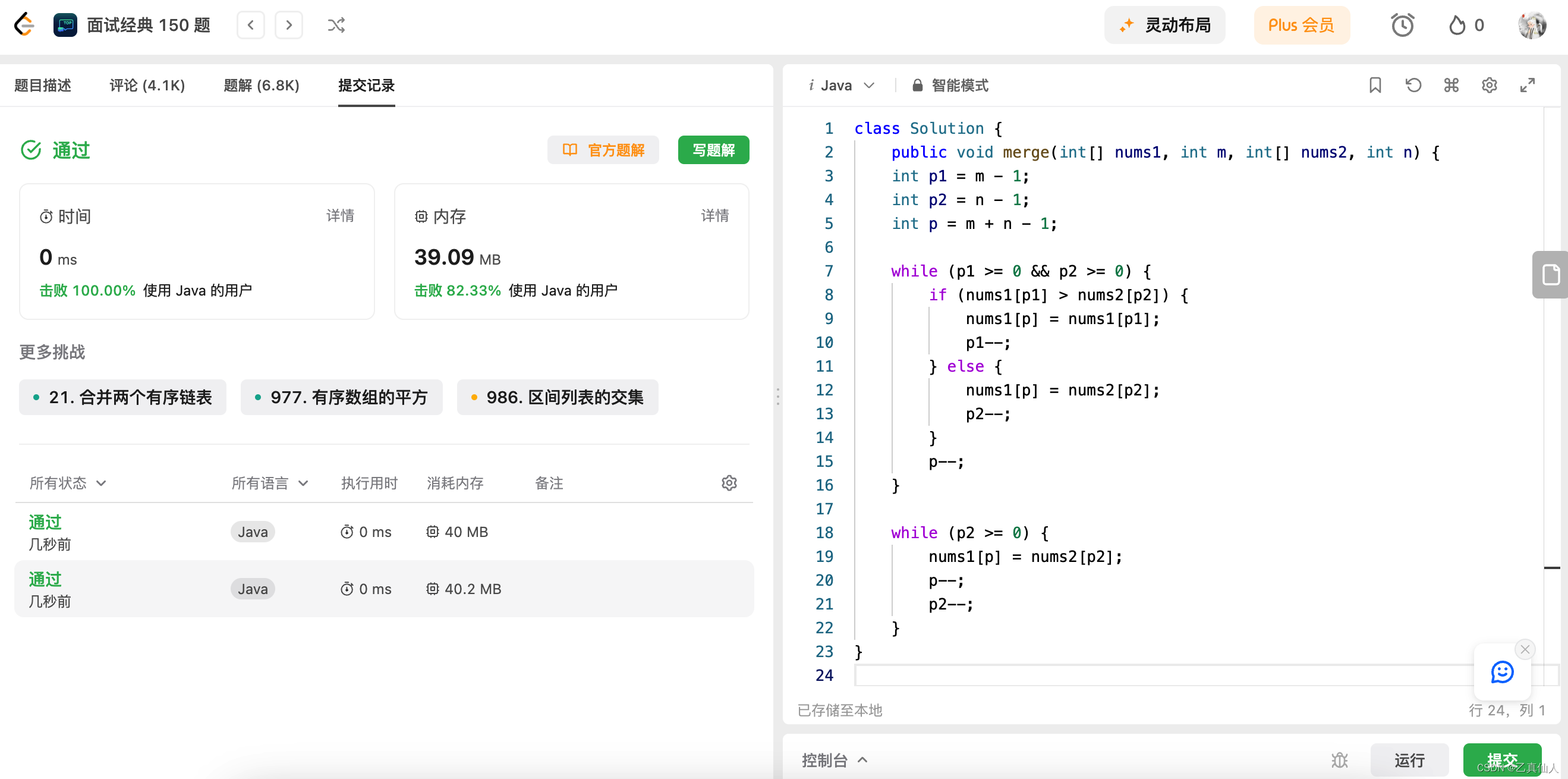
挑战100天 AI In LeetCode Day01(1)
挑战100天 AI In LeetCode Day01(1) 一、LeetCode介绍二、LeetCode 热题 HOT 100-12.1 题目2.2 题解 三、面试经典 150 题-13.1 题目3.2 题解 一、LeetCode介绍 LeetCode是一个在线编程网站,提供各种算法和数据结构的题目,面向程序…...
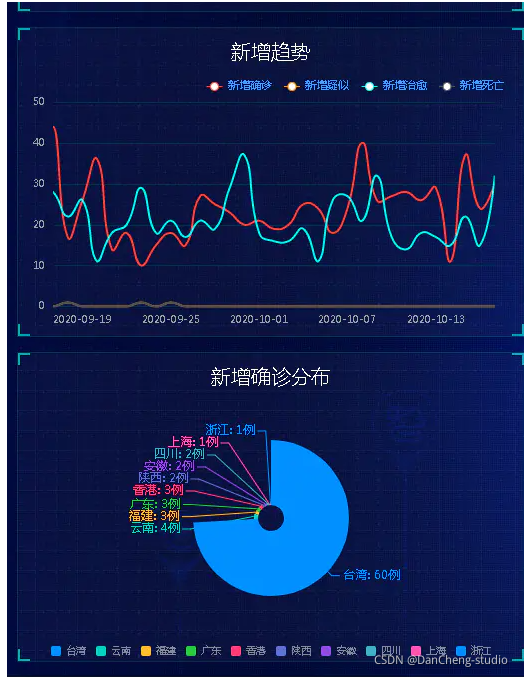
大数据疫情分析及可视化系统 计算机竞赛
文章目录 0 前言2 开发简介3 数据集4 实现技术4.1 系统架构4.2 开发环境4.3 疫情地图4.3.1 填充图(Choropleth maps)4.3.2 气泡图 4.4 全国疫情实时追踪4.6 其他页面 5 关键代码最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 大数据疫…...

uniapp调起拨打手机号
您可以使用uniapp提供的API来调起拨打手机号的功能。具体步骤如下: 在template标签内添加一个按钮,例如: <template><view><button type"primary" click"callPhone">拨打客服电话</button><…...
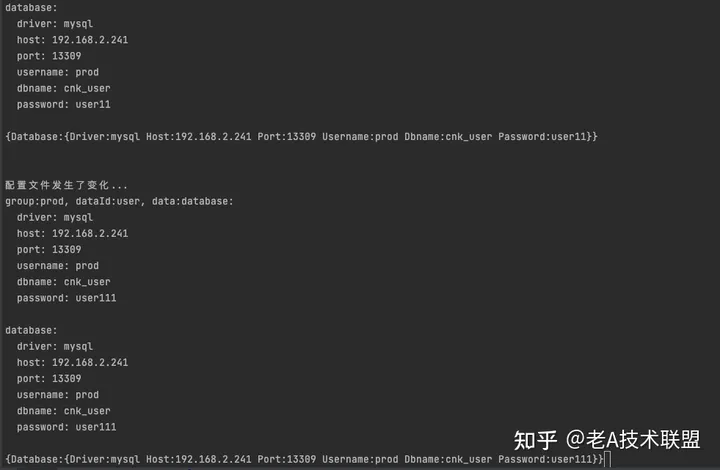
nacos配置中心docker部署、配置及 goLang 集成使用
为什么需要配置中心 平时我们写一个demo的时候,或者说一个单体的应用,都会有一个配置文件,不管是 json文件或者yaml文件,里面包含了redis,mysql,es等信息,如果我们修改了配置文件,往往我们需要重启&#x…...
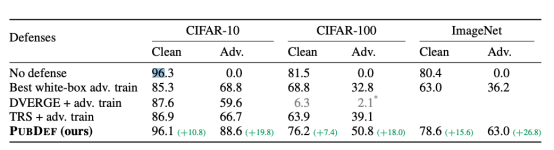
PubDef:使用公共模型防御迁移攻击
对抗性攻击对机器学习系统的可靠性和安全性构成了严重威胁。通过对输入进行微小的变动,攻击者就可以导致模型生成完全错误的输出。防御这种攻击是一个很活跃的研究领域,但大多数提议的防御措施都存在重大的缺点。 这篇来自加州大学伯克利分校研究人员的…...
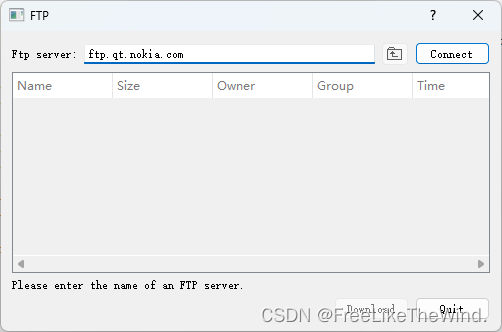
【QT5之QFtp模块】编译及使用
下载 传送门:https://github.com/qt/qtftp 或者 git clone https://github.com/qt/qtftp.git 下载ZIP,解压待用。 编辑 使用QtCreator打开qtftp.pro; 修改如下: qtftp.pro中,将第21行注释; src/qftp.pro中,将第4行…...

数据结构 编程1年新手视角的平衡二叉树AVL从C与C++实现②
接下来,是数据的插入 我们需要对数据插入的结点先进行判断,有如下三个情况 当插入的数据value<结点的value,应该递归地插入该结点的左子树(的左子树...的左子树) 当插入的数据value>结点的value,应…...

代码随想录二刷Day 59
647. 回文子串 这个题的dp定义想不到,递推公式也想不到但是看题解都很容易理解,遍历顺序不太好理解。 class Solution { public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false)…...

由一个自动化脚本运维展开的思考
今天分享一个思路,如何通过脚本集中管理程序的启停。减少人工的介入。 例子 好的,这里有一个基本的shell脚本示例,你可以根据你的具体需求进行修改。 启动脚本(start.sh): #!/bin/bash ./test_server_1…...

STM32F103C8T6第二天:按键点灯轮询法和中断法、RCC、电动车报警器(振动传感器、继电器、喇叭、433M无线接收发射模块)
1. 点亮LED灯详解(307.11) 标号一样的导线在物理上是连接在一起的。 将 PB8 或 PB9 拉低,就可以实现将对应的 LED 灯点亮。常用的GPIO HAL库函数: void HAL_GPIO_Init(GPIO_TypeDef *GPIOx, GPIO_InitTypeDef *GPIO_Init);//I/…...
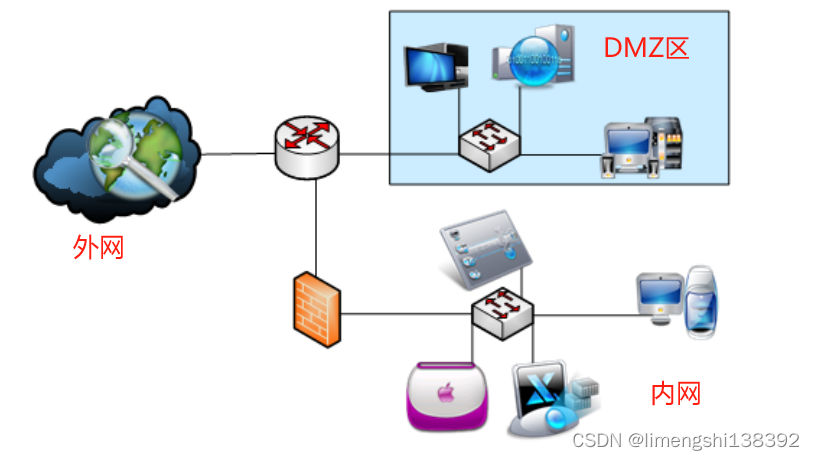
路由器基础(九):防火墙基础
防火墙 (Fire Wall) 是网络关联的重要设备,用于控制网络之间的通信。外部网络用户的访问必须先经过安全策略过滤,而内部网络用户对外部网络的访问则无须过滤。现在的防火墙还具有隔离网络、提供代理服务、流量控制等功能。 一、三种防火墙技术 常见的…...
免费(daoban)gpt,同时去除广告
一. 内容简介 免费(daoban)gpt,同时去除广告,https://chat18.aichatos.xyz/,也可当gpt用,就是有点广告,大家也可以支持一下 二. 软件环境 2.1 Tampermonkey 三.主要流程 3.1 创建javascript脚本 点击添加新脚本 …...
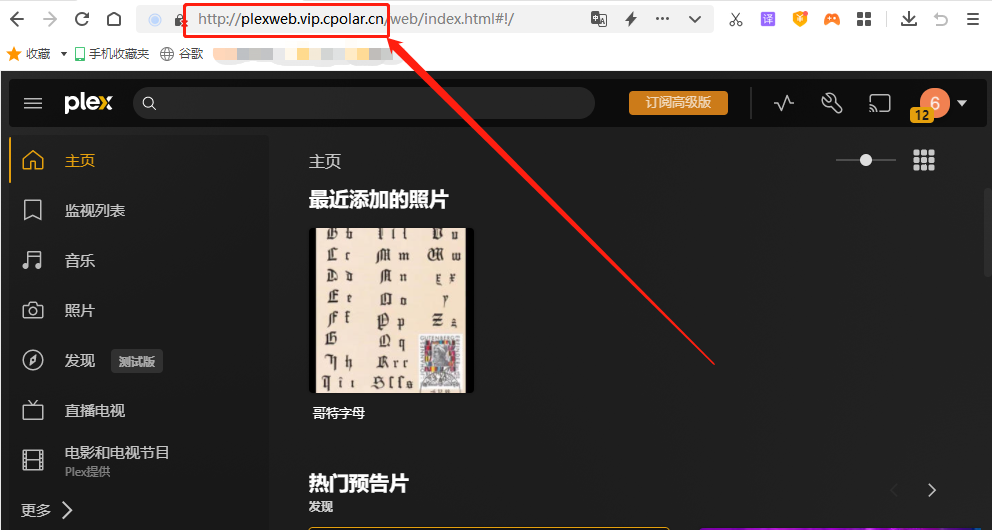
如何使用Plex在Windows系统上搭建一个全能私人媒体影音站点
文章目录 1.前言2. Plex网站搭建2.1 Plex下载和安装2.2 Plex网页测试2.3 cpolar的安装和注册 3. 本地网页发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1.前言 用手机或者平板电脑看视频,已经算是生活中稀松平常的场景了,特别是各…...

vue如何实现视频全屏切换
最近项目开发中遇到一个视频窗口全屏切换功能,为此在这里做个记录。 具体的实现思路: <template><div class"content-box"><div class"container"><div id"screen" class"screen"><…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
