思维模型 布里丹毛驴效应
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。犹豫不决是病,得治~
1 布里丹毛驴效应的应用
1.1 犹豫不决的产品“施乐 914”
20 世纪 60 年代,美国一家名为施乐(Xerox)的公司在复印机市场上占据了主导地位。然而,随着日本企业的进入,施乐的市场份额逐渐下降。为了应对竞争,施乐公司决定开发一款全新的复印机,名为“施乐 914”。
在开发过程中,施乐公司面临了许多技术和设计上的选择。例如,应该使用哪种技术来实现复印功能,应该采用哪种设计风格来吸引消费者等。然而,由于公司内部的犹豫不决和内部争斗,施乐公司花费了数年时间才完成了“施乐 914”的开发。
当“施乐 914”最终推向市场时,已经错过了最佳的上市时机。此时,市场上已经有了其他更加先进和便宜的复印机产品,而施乐公司的产品已经过时。最终,“施乐 914”并没有取得预期的成功,施乐公司也因此失去了在复印机市场上的领先地位。
布里丹毛驴效应在商业决策中是非常常见的。如果决策者不能及时做出决策,或者在面对众多选择时犹豫不决,就可能会错失市场机会,导致商业失败。
1.2 犹豫不决的农民大叔
有一个农民,他有一头驴和一些干草。他需要把干草运到市场上卖,但驴一次只能驮一定量的干草。如果他只驮一次,那么他可以在一天内完成运输,但如果他需要分多次运输,那么他需要花费更多的时间和精力。
这个农民面临两个选择:他可以只驮一次干草,这样他可以在一天内完成运输并获得一定的收益;或者他可以分多次运输干草,这样他可以获得更多的收益,但需要花费更多的时间和精力。
然而,这个农民犹豫不决,他不知道应该选择哪种方式来运输干草。他一直在思考和比较这两个选择,最终错过了最佳的运输时机,导致干草腐烂,无法出售,最终损失惨重。
在面对多个选择时,如果决策者不能及时做出决策,或者在面对众多选择时犹豫不决,就可能会错失市场机会,导致经济损失。
1.3 管理决策中的“布里丹毛驴效应”
20 世纪 60 年代,美国一家著名的电子公司在研发一种新型计算机时,面临着两个选择:一是采用新技术,开发一款全新的计算机;二是在现有技术基础上进行改进,推出一款升级版计算机。
公司的管理团队在这个问题上犹豫不决,他们反复比较这两个选择的优缺点,考虑了各种可能的后果,但始终无法做出决定。最终,公司决定同时进行两个项目,希望能够在开发过程中找到更好的解决方案。
然而,这个决定导致了资源的分散和管理的混乱。两个项目之间存在着竞争和冲突,导致了项目的延误和成本的增加。最终,公司不得不放弃了其中一个项目,造成了巨大的损失。
在面对多个选择时,如果决策者不能及时做出决策,或者在面对众多选择时犹豫不决,就可能会错失机会,导致不良后果。
1.4 择偶中的布里丹毛驴效应
有一位年轻女子面临两个婚姻选择。一个男子是稳定的上班族,提供稳定的收入和舒适的生活,但缺乏激情和浪漫;另一个男子是自由职业者,充满激情和创造力,但收入不稳定,生活也相对不稳定。
这位年轻女子犹豫不决,无法做出决策。她反复比较这两个男子的优缺点,考虑了各种可能的后果,但始终无法做出决定。最终,她错过了这两个男子,不得不重新开始寻找自己的真爱。
这个故事说明了在面对多个选择时,如果决策者不能及时做出决策,或者在面对众多选择时犹豫不决,就可能会错失机会,导致不良后果。
1.5 选择工作的布里丹毛驴效应
有一个年轻人,他同时收到了两份工作邀请。一份工作提供了稳定的收入和良好的福利,但工作内容相对单调;另一份工作则提供了更有挑战性的工作内容和更大的发展空间,但收入和福利相对不稳定。
这个年轻人犹豫不决,无法做出决策。他反复比较这两份工作的优缺点,考虑了各种可能的后果,但始终无法做出决定。最终,他错过了这两份工作,不得不重新开始寻找工作。
这个故事说明了在面对多个选择时,如果决策者不能及时做出决策,或者在面对众多选择时犹豫不决,就可能会错失机会,导致不良后果。
2 模型 布里丹毛驴效应
2.1 什么是 布里丹毛驴效应?
布里丹毛驴效应,是由法国哲学家布里丹提出的一种心理现象。指的是在决策过程中,因为决策者面对众多选择时犹豫不决、难以取舍,最终导致决策失败的现象。
这个效应源于一个寓言故事:有一头驴站在两堆干草中间,左边的干草和右边的干草距离相等,驴不知道应该选择哪一堆干草,于是一直犹豫不决,最终饿死在两堆干草之间。
这个故事说明了在决策过程中,如果决策者缺乏明确的目标和价值观,或者面临的选择太多,就容易陷入犹豫不决的境地,无法做出正确的决策,从而导致失败。
因此,布里丹毛驴效应提醒我们,在面对众多选择时,应该明确自己的目标和价值观,分析各个选项的优缺点,然后果断做出决策,避免犹豫不决。同时,也应该学会放弃一些不重要的选择,集中精力去追求最重要的目标。
2.2 为什么会有 布里丹毛驴效应?
布里丹毛驴效应产生的原因有很多,一些原因如下:
- 缺乏明确的目标和价值观:决策者没有明确的目标和价值观,不知道自己想要什么,因此在面对众多选择时感到无所适从。
- 缺乏信息和经验:决策者可能缺乏足够的信息和经验,无法准确评估各个选项的优缺点,因此难以做出决策。
- 选择太多:决策者面临的选择太多,导致其难以选择,感到无所适从。
- 害怕承担后果:决策者可能害怕做出错误的决策,承担后果,因此犹豫不决。
- 心理压力:决策者可能面临心理压力,例如时间压力、社会压力等,导致其难以冷静思考和做出决策。
- 个人性格和心理特征:某些人可能天生就比较犹豫不决,或者存在一些心理障碍,例如选择困难症等,导致其难以做出决策。
总之,布里丹毛驴效应产生的原因是多种多样的,不同的人可能有不同的原因。为了避免布里丹毛驴效应,我们应该明确自己的目标和价值观,收集足够的信息和经验,学会放弃一些不重要的选择,冷静思考,勇敢承担后果,以及寻求他人的帮助和建议等。
3 模型简图

相关文章:

思维模型 布里丹毛驴效应
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。犹豫不决是病,得治~ 1 布里丹毛驴效应的应用 1.1 犹豫不决的产品“施乐 914” 20 世纪 60 年代,美国一家名为施乐(Xerox)的公司…...
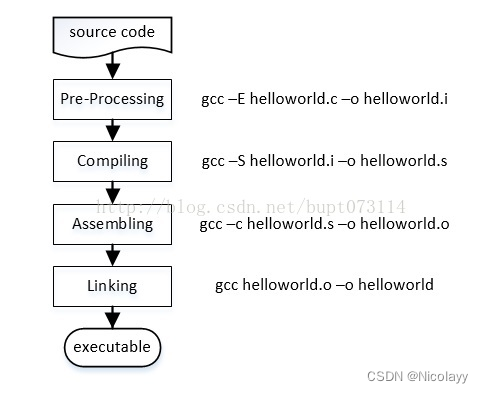
预处理、编译、汇编、链接
1.预处理 宏替换去注释引入头文件 #之后的语句都是预处理语句, #include<iostream> 将该文件的内容拷贝到现有文件中, 2.编译 3.汇编 4.链接 gcc 基于C/C的编译器 补充说明 gcc命令 使用GNU推出的基于C/C的编译器,是开放源代…...

面试问题?
1.面向对象的特征? 2.开放闭合 3.java中的泛型可以用基本类型吗? 4.重载和重写的区别? 5.string、stringbuffer、stringbuilder? 6.单例模式的实现方式有哪几种? 7.volicate除了保证 8.sy是重量级锁还是轻量级锁ÿ…...

pytorch 笔记:PAD_PACKED_SEQUENCE 和PACK_PADDED_SEQUENCE
1 PACK_PADDED_SEQUENCE 1.0 功能 将填充的序列打包成一个更加紧凑的形式这样RNN、LSTM和GRU等模型可以更高效地处理它们,因为它们可以跳过不必要的计算 1.2 基本使用方法 torch.nn.utils.rnn.pack_padded_sequence(input, lengths, batch_firstFalse, enforce_…...
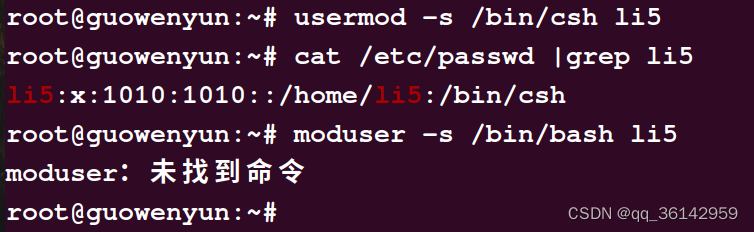
Ubuntu 创建用户
在ubuntu系统中创建用户,是最基本的操作。与centos7相比,有较大不同。 我们通过案例介绍,讨论用户的创建。 我们知道,在linux中,有三类用户:超级管理员 root 具有完全权限;系统用户 bin sys a…...

华为政企路由器产品集
产品类型产品型号产品说明 maintainProductA821 E_2*10GE/GE/FE(o)8*GE/FE(o)8*GE/FE(e),1*交流电源华为企业云端NetEngine A800 E综合业务一体化接入路由器是华为公司面向云时代推出的一款产品,用于企业快速接入网络,具备易部署、易运维、高性能、高…...
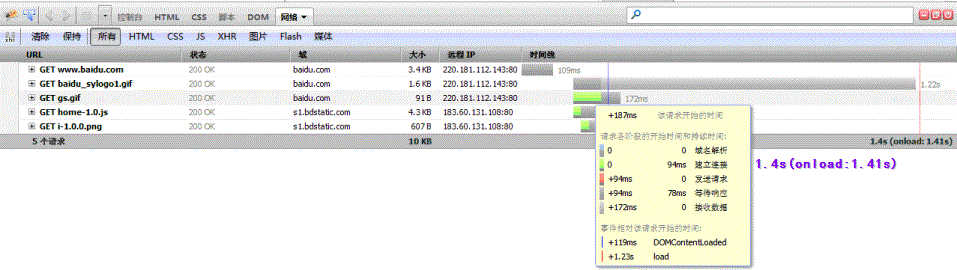
性能测试知多少---了解前端性能
我的上一篇博文中讲到了响应时间,我们在做性能测试时,能过工具可以屏蔽客户端呈现时间,通过局域网的高宽带可以忽略数据传输速度的障碍。这并不是说他们不会对系统造成性能影响。相反,从用户的感受来看,虽然传输速度受…...

Docker-compose容器群集编排管理工具
目录 Docker-compose 1、Docker-compose 的三大概念 2、YAML文件格式及编写注意事项 1)使用 YAML 时需要注意下面事项 2)ymal文件格式 3)json格式 3、Docker Compose配置常用字段 4、Docker-compose的四种重启策略 5、Docker Compose…...

Python 深度学习导入的一些包的说明
Python 深度学习导入的一些包的说明 这段代码导入了一些Python库和模块,并定义了一些数据转换操作。 from future import print_function, division:这是一个Python 2和Python 3兼容性的导入语句。它确保在Python 2中使用Python 3的print函数和除法运算符…...

劲升逻辑与安必快、鹏海运于进博会签署合作协议,助力大湾区外贸高质量发展
新中经贸与投资论坛签约现场 中国上海,2023 年 11 月 6 日——第六届进博会期间,由新加坡工商联合总会主办的新中经贸与投资论坛在上海同期举行。跨境贸易数字化领域的领导者劲升逻辑与安必快科技(深圳)有限公司(简称…...
hivesql,sql 函数总结:
1、NVL函数与Coalesce差异 -- select nvl(null,8); -- 结果是 8 -- select nvl(,7); -- 结果是"" -- select coalesce(null,null,9); -- 结果是 9 -- select coalesce("",null,9); -- 结果是 "" 1.2、 NVL函数与Coalesce差异 …...

前端js实现井字游戏和版本号对比js逻辑【适用于vue和react】
// 实现 compareVersion 方法,用于比较两个版本号(version1、version2) * 如果version1 > version2,返回1; * 如果version1 < version2,返回-1; * 其他情况,返回0。 * 版本号规…...

unity 通过Andriod arr 访问 手机自带的浏览器
unity 通过Andriod arr 访问 手机自带的浏览器 using System.Collections; using System.Collections.Generic; using System.IO; using UnityEngine; using UnityEngine.UI;public class OpenURL : MonoBehaviour {public Button button;string url "http://192.168.1.…...

MySQL -- 索引
MySQL – 索引 文章目录 MySQL -- 索引一、索引简介1.简介2.索引效率的案例 二、认识磁盘1.磁盘2.结论3.磁盘随机访问(Random Access)与连续访问(Sequential Access) 三、MySQL 与磁盘交互基本单位1.基本单位2.MySQL中的数据管理 五、索引的理解1.索引案例2.单页mysql page3.管…...
)
23ccpc(最长上升子序列题解)
你原本有一个 1 到 n 的排列但是不慎地你遗忘了它但是你记得以 第i个位置 结尾的最长上升子序 列的长度数组 an 现在希望你能够构造一个符合条件的排列 p 如果不存在符合上述条件的排列 p 则输出 −1。 这里定义以 第i位置 结尾的最长上升子序列的长度为符合…...

BUUCTF easycap 1
BUUCTF:https://buuoj.cn/challenges 题目描述: 下载附件,解压得到一个.pcap文件。 密文: 解题思路: 1、这道题和它的名字一样,真的很easy。双击easycap.pcap文件,打开Wireshark。在Wireshark中…...
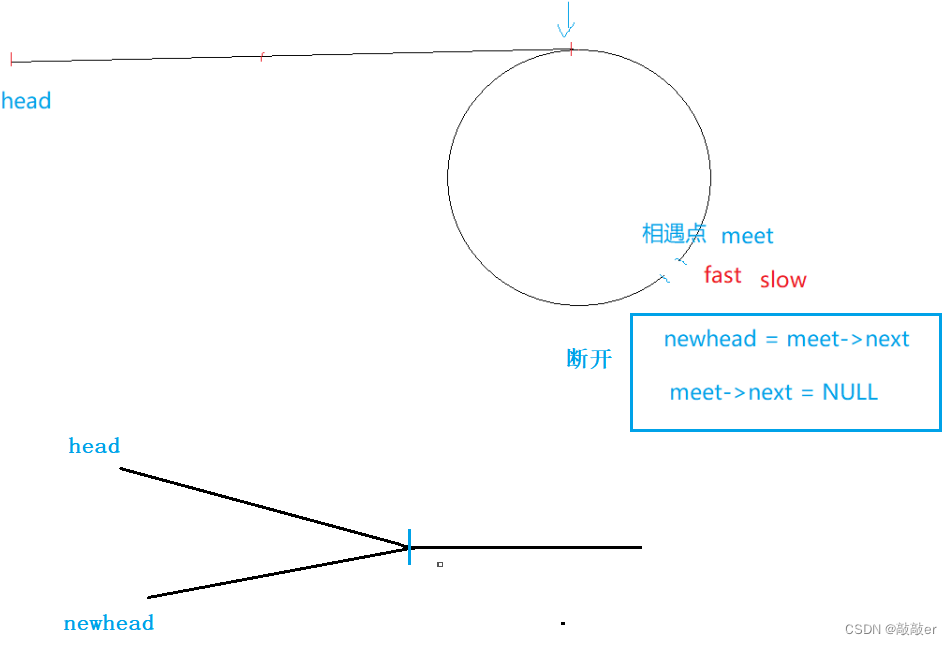
[LeetCode]-160. 相交链表-141. 环形链表-142.环形链表II-138.随机链表的复制
目录 160.相交链表 题目 思路 代码 141.环形链表 题目 思路 代码 142.环形链表II 题目 思路 代码 160.相交链表 160. 相交链表 - 力扣(LeetCode)https://leetcode.cn/problems/intersection-of-two-linked-lists/description/ 题目 给你两个…...

聊一聊关于手机Charge IC的电流流向
关于手机Charge,小白在以前的文章很少讲,一是这部分东西太多,过于复杂。二是总感觉写起来欠缺点什么。但后来想一想,本是抱着互相学习来写文章的心理态度,还是决定尝试写一些。 关于今天要讲的关于手机Charge的内容&a…...

【k8s】pod调度——亲和,反亲和,污点,容忍
官方网址:https://kubernetes.io/zh/docs/concepts/scheduling-eviction/assign-pod-node/ 一、亲和性 (1)节点亲和性 pod.spec.nodeAffinity ●preferredDuringSchedulingIgnoredDuringExecution:软策略 p开头 ●requiredDuri…...
分享者 - 携程旅游创作者搬砖项目图文教程
大家好!携程这个出行旅游平台相信大家都不陌生吧。 每天都有大量的旅客在里面浏览攻略,寻找灵感和旅游建议。 那么,我们的项目就是把一些优质的小红书平台上的旅游攻略或作品,经过处理后搬运到携程平台上发布。 这个项目如何操作呢…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
