【学习笔记】[COCI2018-2019#1] Teoretičar
首先,可以发现 C C C等于所有点度数的最大值,我们能用到的颜色数目为 2 x ≥ C 2^x\ge C 2x≥C。
考虑分治,将边集划分为 E = E 1 + E 2 E=E_1+E_2 E=E1+E2,使得 E 1 , E 2 E_1,E_2 E1,E2中点度数的最大值都不超过 2 x − 1 2^{x-1} 2x−1。这样,我们将 [ 1 , 2 x − 1 ] [1,2^{x-1}] [1,2x−1]中的颜色分配给 E 1 E_1 E1, [ 2 x − 1 + 1 , 2 x ] [2^{x-1}+1,2^x] [2x−1+1,2x]中的颜色分配给 E 2 E_2 E2,就可以递归到子问题。显然当 C = 1 C=1 C=1时,可以将所有边染成同一个颜色。
显然,我们可以用欧拉回路解决这个问题。但是这个做法常数比较大。考虑 CF1499G Graph Coloring 的做法,维护若干个环和若干条端点互不相同的链(因为是二分图,所以环的长度一定是偶数),这可以用带权并查集维护。注意并查集的维护对象是每条边,合并两条边的时候限制等价于这两条边所属集合不同。
复杂度 O ( m log m ) O(m\log m) O(mlogm)。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
using namespace std;
const int N=2e5+5;
const int M=5e5+5;
int L,R,m,U[M],V[M],du[N],st[N];
int fa[M],val[M],tag[M],res[M];
vector<int>v;
int find(int x){if(fa[x]==x)return x;int tmp=fa[x];fa[x]=find(fa[x]);val[x]^=val[tmp];return fa[x];
}
void upd(int x){find(x);if(!(val[x]^tag[fa[x]])){tag[fa[x]]^=1;}
}
void unionset(int x,int y){int u=find(x),v=find(y);if(u!=v){val[u]=val[x]^val[y]^1,fa[u]=v;}
}
void solve(vector<int>&v,int cur){if(v.size()==0)return;for(auto e:v){fa[e]=e,val[e]=0,tag[e]=0,st[U[e]]=st[V[e]]=0;}int f=0;for(auto e:v){int x=U[e],y=V[e];if(st[x]||st[y])f=1;if(!st[x]&&!st[y]){st[x]=st[y]=e;}else if(!st[x]){upd(st[y]);unionset(e,st[y]);st[x]=e,st[y]=0;}else if(!st[y]){upd(st[x]);unionset(e,st[x]);st[y]=e,st[x]=0;}else{upd(st[x]),upd(st[y]);unionset(e,st[x]),unionset(e,st[y]);st[x]=st[y]=0;}}if(f==0){for(auto e:v)res[e]=1;}else{vector<int>vl,vr;for(auto e:v){find(e);if(val[e]^tag[fa[e]]){vr.pb(e);}else{vl.pb(e);}}solve(vl,cur>>1),solve(vr,cur>>1);for(auto e:vr)res[e]+=cur>>1;}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>L>>R>>m;for(int i=1;i<=m;i++){cin>>U[i]>>V[i],V[i]+=L;du[U[i]]++,du[V[i]]++,v.pb(i);}int dmax=0;for(int i=1;i<=L+R;i++)dmax=max(dmax,du[i]);int x=2;while(x<dmax)x<<=1;solve(v,x);cout<<x<<"\n";for(int i=1;i<=m;i++)cout<<res[i]<<"\n";
}
相关文章:

【学习笔记】[COCI2018-2019#1] Teoretičar
首先,可以发现 C C C等于所有点度数的最大值,我们能用到的颜色数目为 2 x ≥ C 2^x\ge C 2x≥C。 考虑分治,将边集划分为 E E 1 E 2 EE_1E_2 EE1E2,使得 E 1 , E 2 E_1,E_2 E1,E2中点度数的最大值都不超过 2 x − 1 2^…...

64位Office API声明语句第112讲
跟我学VBA,我这里专注VBA, 授人以渔。我98年开始,从源码接触VBA已经20余年了,随着年龄的增长,越来越觉得有必要把这项技能传递给需要这项技术的职场人员。希望职场和数据打交道的朋友,都来学习VBA,利用VBA,起码可以提高…...

C++ day3作业
1> 思维导图 2> 自己封装一个矩形类(Rect),拥有私有属性:宽度(width)、高度(height), 定义公有成员函数: 初始化函数:void init(int w, int h) 更改宽度的函数:set_w(int w) 更改高度的函数:set_h(int h) 输出该矩形的周长和面积函数:void s…...

蓝桥杯官网填空题(方格计数)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 如下图所示,在二维平面上有无数个 11 的小方格。 我们以某个小方格的一个顶点为圆心画一个半径为 50000 的圆。 你能计算出这个圆里有多少个完整的小方…...

【系统架构设计】计算机公共基础知识: 6 知识产权与标准化
一 知识产权 1 保护对象和范围 法律法规名称保护对象及范围注意事项著作权法著作权 文学、绘画、摄影等作品 不需要申请,作品完成就开始保护。 绘画或摄影作品原件出售(赠予)著作权归还原作者,原件拥有者有所有权和展览权。 软件著作权法 计算机软件保护条例 软件著作权 软…...

【新】致远OA从前台XXE到RCE漏洞分析
0x01 前言 致远OA是目前国内最流行的OA系统之一,前几年也曾爆出过多个安全漏洞。致远官方一直对修复漏洞的态度十分积极,目前能有效利用的致远漏洞已经很少了。 和我们之前分享过的通达OA的漏洞类似,这类主流OA系统现在想要直接一步达到RCE的…...
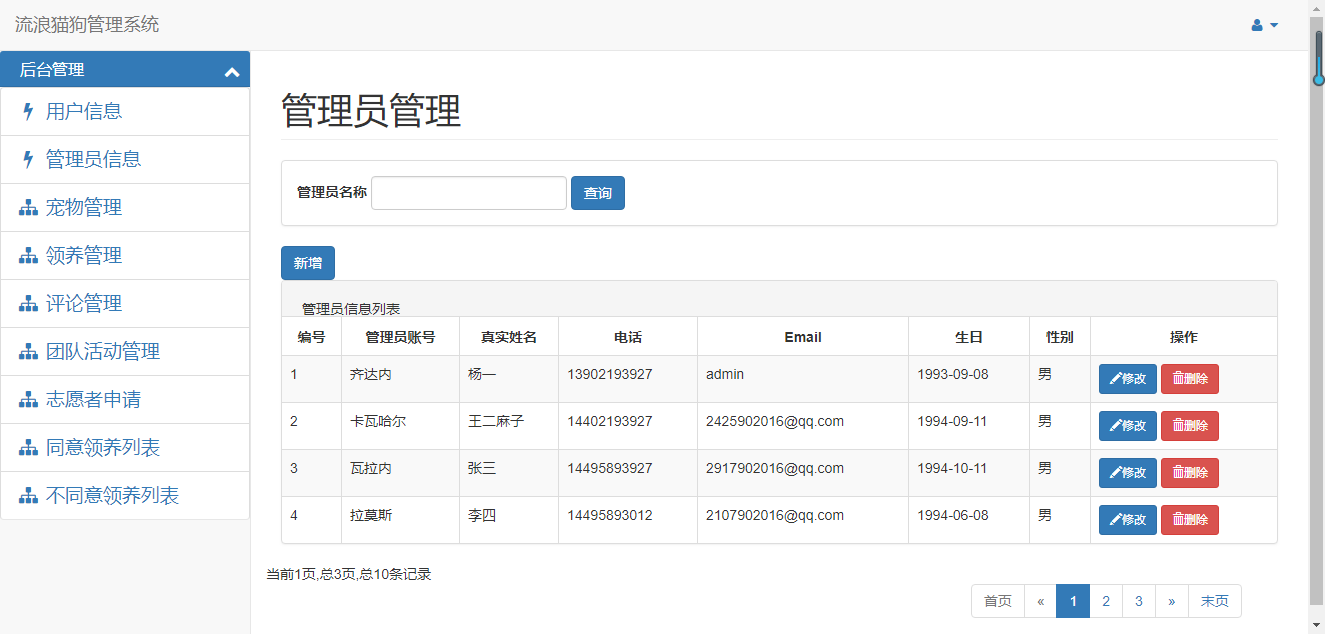
宠物领养系统jsp+servlet+mysql
设计不同用户的操作权限、注册和登录方法。 管理员可以在管理员管理、用户管理、宠物管理、评论管理、团队活动管理、志愿者的申请等等模块中进行查询、添加、删除、修改。 管理员可以在领养管理中通过领养时间查询所有宠物被领养的信息,修改是否同意领养宠物&#…...

MySQL 数据库安全性练习题
数据库安全性 一、实验目的 (1)熟悉通过MySQL对数据进行安全性控制 二、实验环境 Windows 11 MySQL Navicat 三、实验内容 今有以下两个关系模式: 职工(职工号,姓名,年龄,职务,工…...

如何使用Node.js快速创建HTTP服务器并实现公网访问本地Server
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...
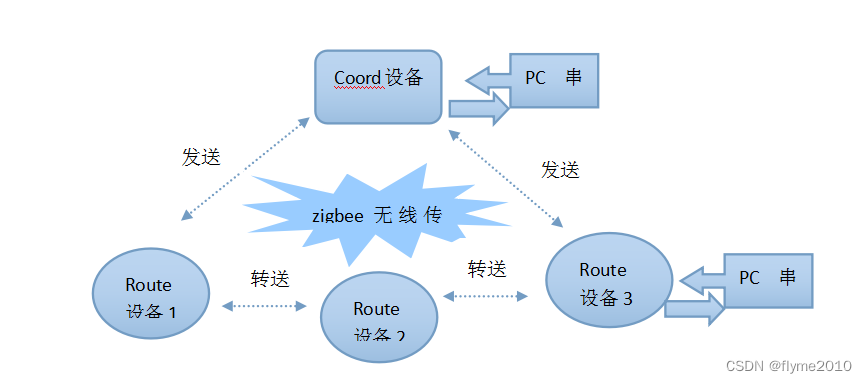
zigbee路灯无线通讯机制
zigbee路灯无线通讯机制 wang20160630 前言 目前路灯上通讯主要有电力载波和无线通讯;各有利弊,众说纷纭;本文不对两种技术进行比较,也不讨论哪种好,毕竟同种通讯模块,有的开发出来稳定,有的…...

asp.net docker-compose添加kafka和redis和zookeeper
docker-compose.yml添加 redis:image: redis:alpinekafka:image: "bitnami/kafka:3.1.1"depends_on:- zookeeperzookeeper:image: "bitnami/zookeeper:3.5.10" docker-compose.override.yml添加 redis:ports:- "6379"kafka:links: - zookeepere…...

2024上海国际人工智能展(CSITF)“创新驱动发展·科技引领未来”
人工智能(Artificial Intelligence,AI)作为当今世界科技发展的关键领域之一,正不断推动着各行各业的创新和变革。作为世界上最大的消费市场之一,中国正在积极努力将AI技术与产业融合并加速推广应用。在这个背景下&…...

汽车标定技术(三)--XCP协议如何支持测量功能
目录 1. 概述 2. 测量方式 -- Poll 3. 测量方式 -- DAQ 3.1 ODT概念模型 3.2 DAQ List概念 3.3 ODT 绝对编号和相对编号 3.4 静态DAQ和动态DAQ模式 (1)静态DAQ (2)动态DAQ 4.小结 1. 概述 在该系列的首篇文章汽车标定技…...

[c++]你最喜爱的stringstream和snprintf性能深入剖析
最近写一个程序中两个差不多的模块,一个使用了snprintf输出中间数据,另一个偷懒使用stringstream。结果你猜怎么着?居然压帧了!!到底是谁拖了性能的后退? 来自阿里云的性能分析实验 我上网一搜࿰…...
windows 用vs创建cmake工程并编译opencv应用项目生成exe流程简述
目录 前言一、安装opencv(1)下载(2)双击安装(3)环境变量和system文件夹设置 二、打开vs创建项目三、编辑cpp,.h,cmakelist.txt文件(1)h文件(2&…...
QML 仪表盘小示例
本次项目已发布在CSDN->GitCode,下载方便,安全,可在我主页进行下载即可,后面的项目和素材都会发布这个平台。 个人主页:https://gitcode.com/user/m0_45463480怎么下载:在项目中点击克隆,windows:zip linux:tar.gz tar # .pro TEMPLATE = appTARGET = dialcontrol#…...
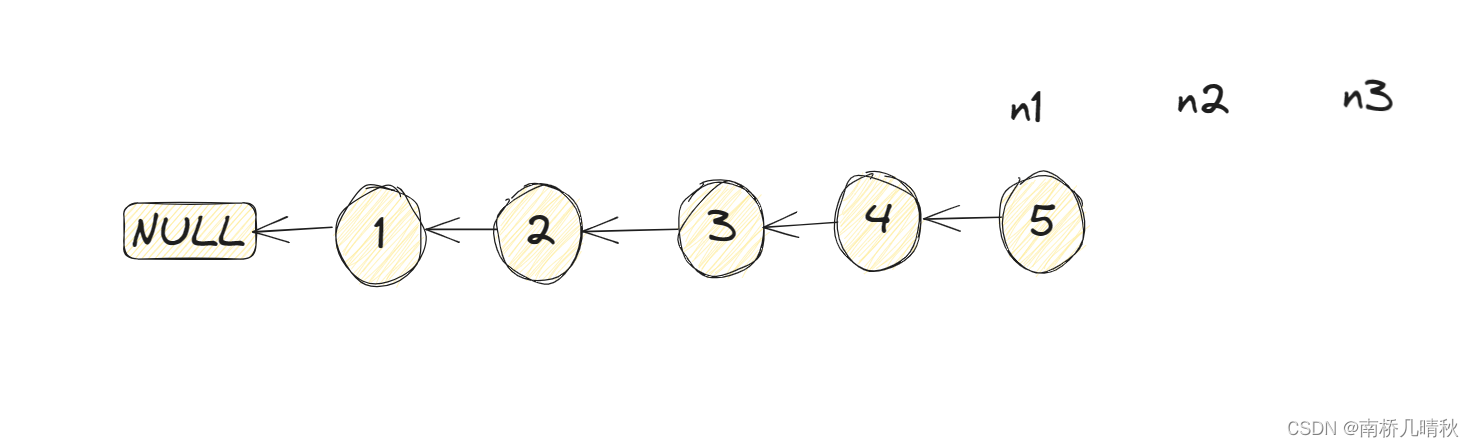
力扣206. 反转链表
题目: 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3:…...
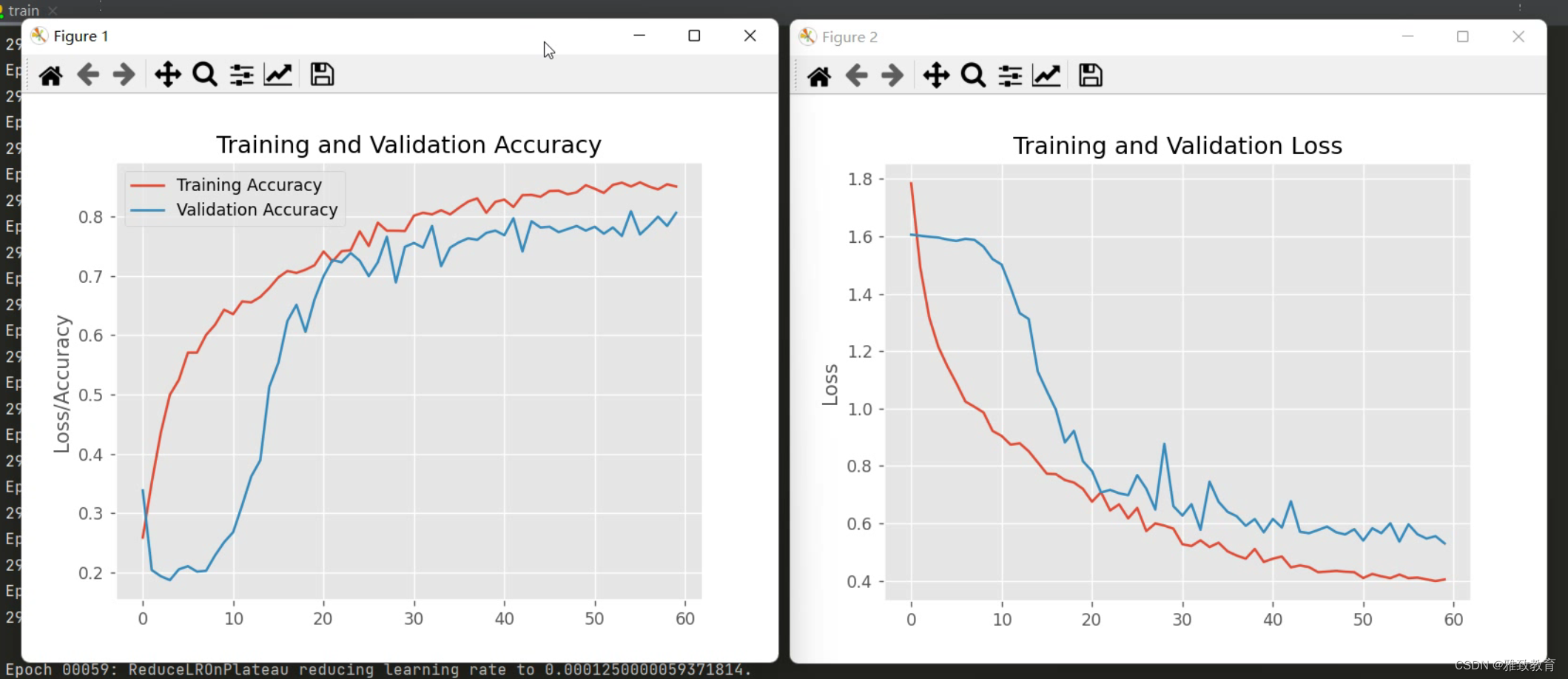
深度学习之基于Tensorflow卷积神经网络花卉识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 深度学习是一种机器学习方法,它通过模拟人脑神经网络的结构和功能来实现对数据的自动分析和学习。卷积神…...

leetcode链表
这几天手的骨裂稍微好一点了,但是还是很疼,最近学校的课是真多,我都没时间做自己的事,但是好在今天下午是没有课的,我也终于可以做自己的事情了。 今天分享几道题目 移除链表元素 这道题我们将以两种方法开解决&…...
Kali Linux渗透测试的艺术
Kali Linux(Kali)是专门用于渗透测试的Linux操作系统,它由BackTrack 发展而来。在整合了IWHAX、WHOPPIX 和Auditor 这3 种渗透测试专用Live Linux 之后,BackTrack正式改名为Kali Linux。 BackTrack是相当著名的Linux发行版本。在…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
