【MogDB/openGauss的三种函数稳定性关键字】
一、ORACLE中的类似的函数稳定性关键字(DETERMINISTIC)
在ORACLE里,function有着一个DETERMINISTIC参数,它表示一个函数在输入不变的情况下输出是否确定,只要输入的参数一样,返回的结果一定一样的,以保证函数对于任何输入总是完全相同的方式处理参数,oracle的内置函数 UPPER,TRUNC 等都是 deterministic 函数。具体例子如下:
----带DETERMINISTIC的现象
create or replace function f_t(i_p int) return number DETERMINISTIC isi_rtn number;begini_rtn := i_p * dbms_random.value(1,10);return i_rtn;end;/select LEVEL,f_t(1) FROM DUAL CONNECT BY LEVEL<=10;----不带DETERMINISTIC的现象create or replace function f_t(i_p int) return number isi_rtn number;begini_rtn := i_p * dbms_random.value(1,10);return i_rtn;end;/select LEVEL,f_t(1) FROM DUAL CONNECT BY LEVEL<=10;
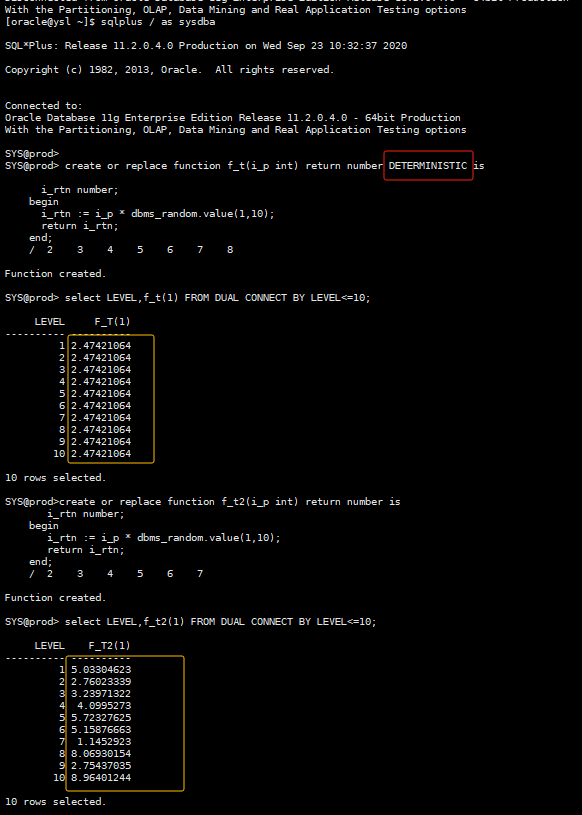
可以看到,带了DETERMINISTIC参数的,多次执行的结果都是一样的,能保证函数的稳定性。
二、MogDB/openGauss的三种函数稳定性状态
而MogDB数据库的函数虽然没有DETERMINISTIC关键字,但是函数也有着类似的三种状态的关键字,分别是immutable、stable和volatile。合理使用着三种不同的状态可以显著改善函数性能。
在数据库里使用\d create function也可以看到这三种状态的关键字提示。
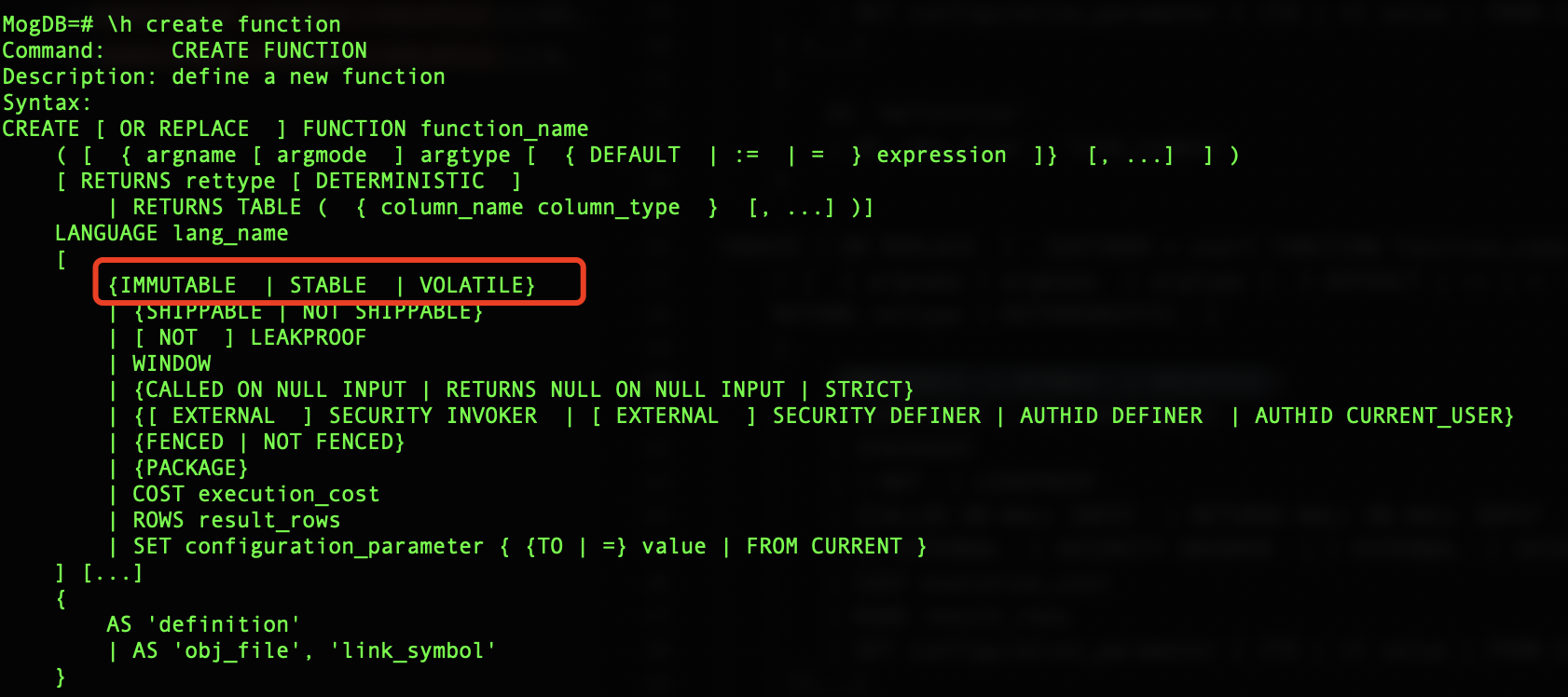
IMMUTABLE(非常稳定)
任何时候调用,只要函数的参数不变结果就不变。 纯函数,执行结果可能会在规划时被预求值并缓存。
允许优化器在一个查询用常量参数调用该函数时提前计算该函数,整数加法操作符底层的函数被 标记为IMMUTABLE。
表示该函数不能修改数据库并且对于给定的参数值总是会返回相同的值。 也就是说,它不会做数据库查找或者使用没有在其参数列表中直接出现的信息。immutable, 和stable非常类似, 但是immutable是指在任何情况下, 只要参数一致, 结果就一致。
STABLE(稳定)
稳定,在一个事务中调用时,只要函数的参数不变结果就不变。
STABLE函数不能修改数据库状态,但是对于相同的参数值,它在一次表扫描中将返回相同的结果。
因而优化器可以将相同参数的多次调用优化成一次调用。在索引扫描条件中允许使用STABLE函数。
在大多数情况下是的。在单个表扫描中,对相同的参数值返回相同的结果,但结果将通过SQL语句进行更改。 结果取决于数据库查找或参数值。 current_timestamp系列函数是 STABLE; 值在执行中不会改变。
immutable和stable很像,显著的区别是优化器对immutable和stable函数的处理上,immutable函数在优化器生成执行计划时会将函数结果替换函数. 也就是函数不在输出的执行计划中, 取而代之的是一个结果常量。stable函数则不会如此, 执行计划输出后还是函数。
immutable和stable在调用次数上的明显区别可以用如下的测试验证出来:
CREATE OR REPLACE FUNCTION func_out_num() RETURNS INTEGER AS
$$
BEGIN
RAISE NOTICE 'Invoke the func.';
RETURN 6;
END;
$$ LANGUAGE PLPGSQL STABLE;select func_out_num() from generate_series(1,10);
alter function func_out_num() immutable;
select func_out_num() from generate_series(1,10);
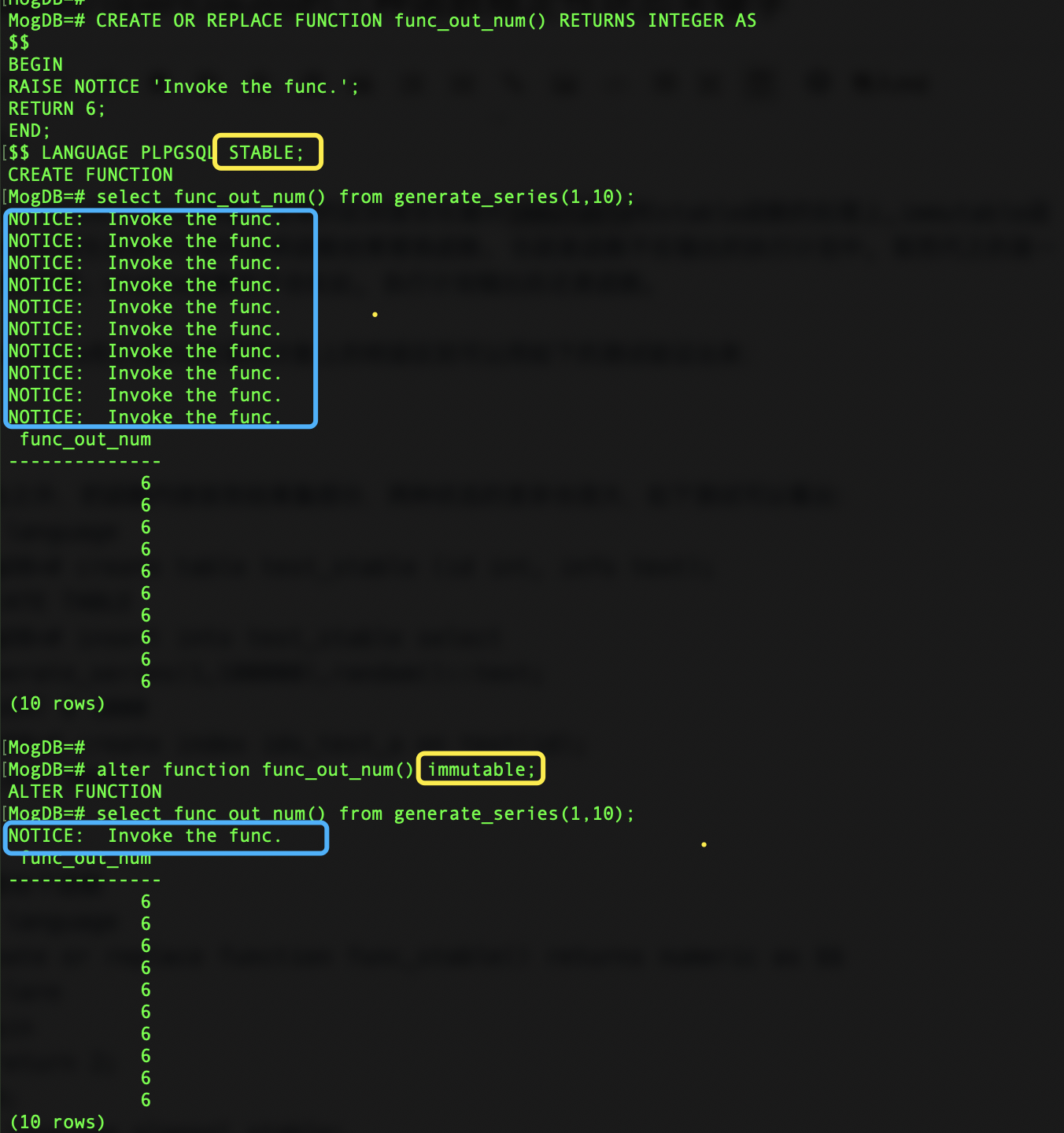
在本例中,当使用STABLE关键字的时候,会按照调用10次函数,而当使用IMMUTABLE关键字时,它会被优化为一次调用。
除此之外,把函数内容放到结果集部分,两种状态的差异也很大,如下测试可以看出:
MogDB=# create table test_stable (id int, info text);
CREATE TABLE
MogDB=# insert into test_stable select generate_series(1,100000),random()::text;
INSERT 0 1000
MogDB=# create index idx_test_a on test(id);
CREATE INDEX
创建如下函数
create or replace function func_stable() returns numeric as $$
declare
begin return 2;
end;
$$ language plpgsql stable; 
使用如下语句可以进行验证两种方式的执行计划时间明显不同。
explain analyze select func_stable() from test_stable;
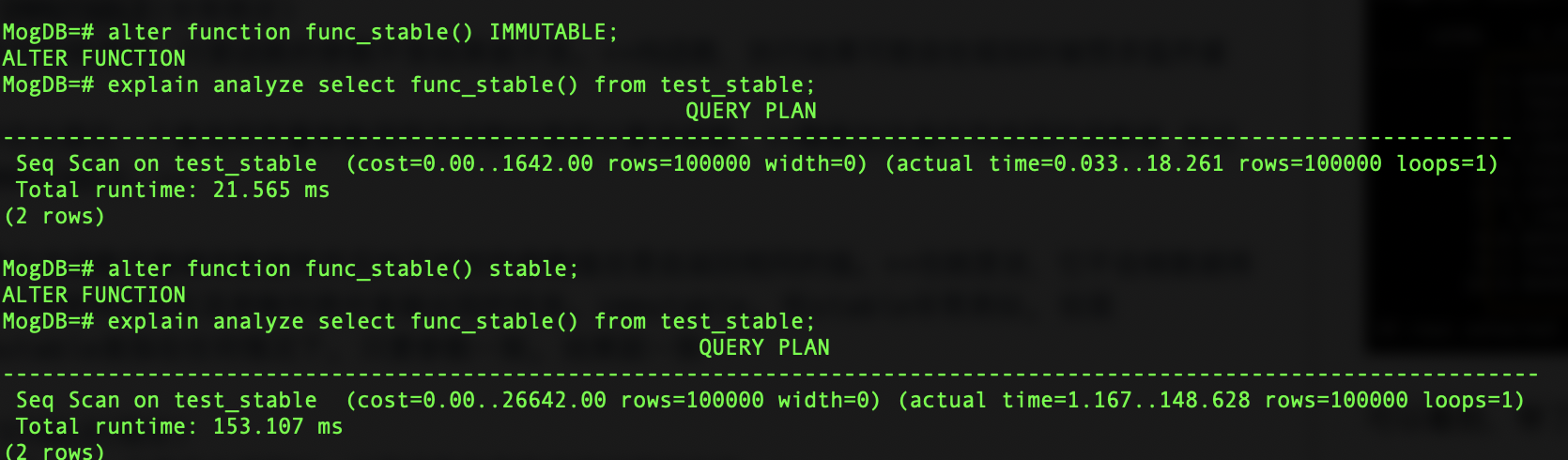
因此,在事务中参数一致则结果一致,且只关注函数的最终结果可以标记为immutable,因为它调用函数的次数少,固化了函数的结果,执行计划的代价较小。但是一般还是建议使用stable,因为它会老老实实的去执行函数,而不是只取一个固化的结果。
VOLATILE(不稳定)
默认为VOLATILE。表示该函数的值在一次表扫描中都有可能改变,因此不能做优化。
VOLATILE函数可以做任何事情,包括修改数据库状态。 在连续调用时即使使用相同的参数,也可能会返回不同的结果。优化器不会优化掉此类函数,每次调用都会重新求值。
在这种意义上,相对较少的数据库函数是不稳定的。 例如: random(), currval(), timeofday()。 任何具有副作用的函数的都不稳定的,即使其结果是可预测的。例如: setval()。
只有函数声明了VOLATILE状态才可以进行update操作。
具体的验证如下所示:
MogDB=# create table test_volatile (id int, info text);
CREATE TABLE
MogDB=# insert into test_volatile select generate_series(1,1000),random()::text;
INSERT 0 1000
MogDB=# create index idx_test on test(id);
CREATE INDEX
然后建立测试的函数
create or replace function func_volatile(ida int) returns text as $$
declare result text;
begin update test_volatile set info='xiaoguaishou' where id=ida returning info into result; return result;
end;
$$ language plpgsql volatile;
可以看到测试结果:
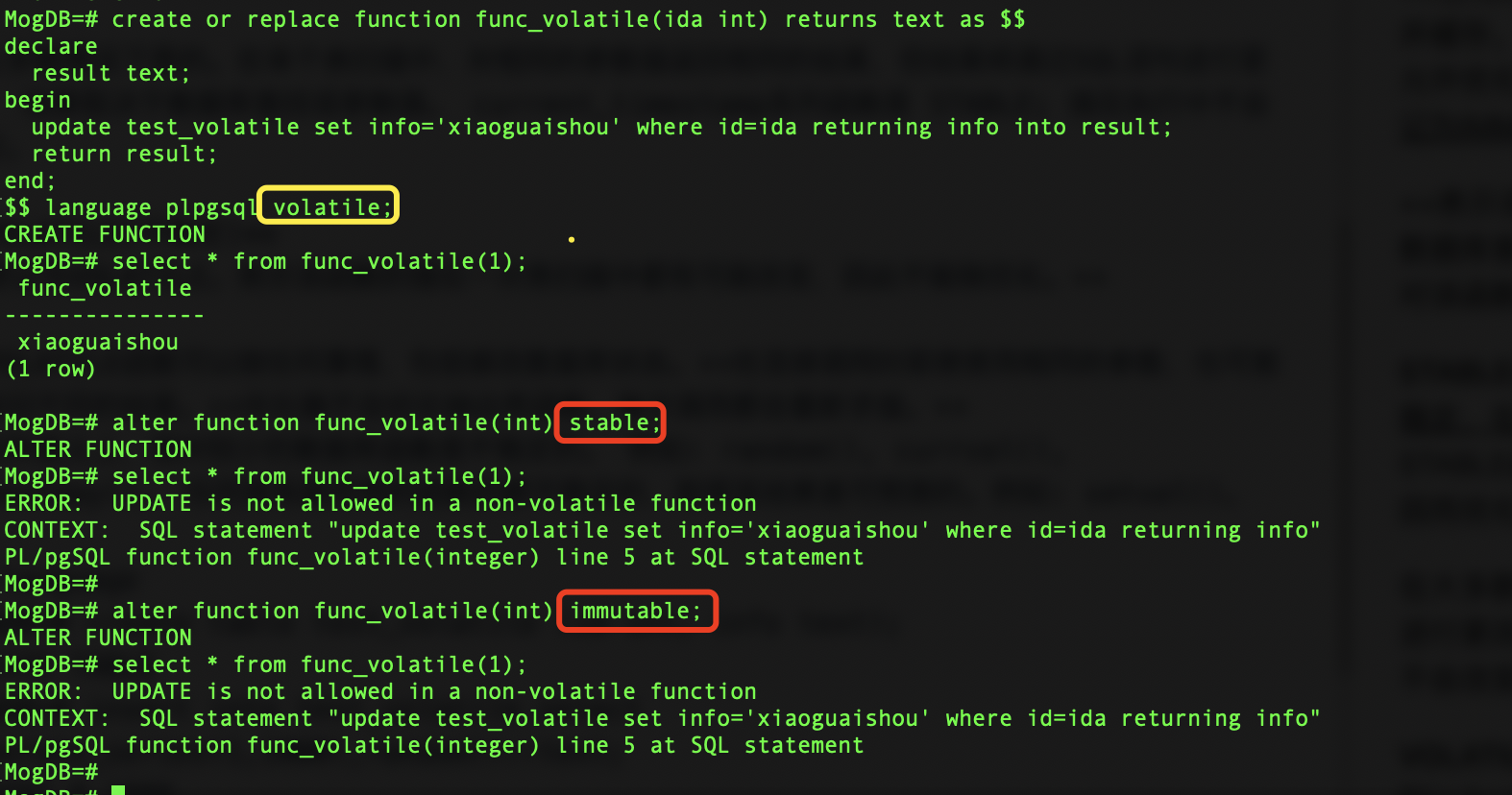
相关文章:

【MogDB/openGauss的三种函数稳定性关键字】
一、ORACLE中的类似的函数稳定性关键字(DETERMINISTIC) 在ORACLE里,function有着一个DETERMINISTIC参数,它表示一个函数在输入不变的情况下输出是否确定,只要输入的参数一样,返回的结果一定一样的…...

java-对Integer.MAX_VALUE做加法
public static void main(String[] args) {int maxValue Integer.MAX_VALUE;System.out.println("maxValue1 " (maxValue1));System.out.println("maxValue2 " (maxValue2));System.out.println("maxValue3 " (maxValue3));}//结果 maxVa…...

【学习笔记】[COCI2018-2019#1] Teoretičar
首先,可以发现 C C C等于所有点度数的最大值,我们能用到的颜色数目为 2 x ≥ C 2^x\ge C 2x≥C。 考虑分治,将边集划分为 E E 1 E 2 EE_1E_2 EE1E2,使得 E 1 , E 2 E_1,E_2 E1,E2中点度数的最大值都不超过 2 x − 1 2^…...

64位Office API声明语句第112讲
跟我学VBA,我这里专注VBA, 授人以渔。我98年开始,从源码接触VBA已经20余年了,随着年龄的增长,越来越觉得有必要把这项技能传递给需要这项技术的职场人员。希望职场和数据打交道的朋友,都来学习VBA,利用VBA,起码可以提高…...

C++ day3作业
1> 思维导图 2> 自己封装一个矩形类(Rect),拥有私有属性:宽度(width)、高度(height), 定义公有成员函数: 初始化函数:void init(int w, int h) 更改宽度的函数:set_w(int w) 更改高度的函数:set_h(int h) 输出该矩形的周长和面积函数:void s…...

蓝桥杯官网填空题(方格计数)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 如下图所示,在二维平面上有无数个 11 的小方格。 我们以某个小方格的一个顶点为圆心画一个半径为 50000 的圆。 你能计算出这个圆里有多少个完整的小方…...

【系统架构设计】计算机公共基础知识: 6 知识产权与标准化
一 知识产权 1 保护对象和范围 法律法规名称保护对象及范围注意事项著作权法著作权 文学、绘画、摄影等作品 不需要申请,作品完成就开始保护。 绘画或摄影作品原件出售(赠予)著作权归还原作者,原件拥有者有所有权和展览权。 软件著作权法 计算机软件保护条例 软件著作权 软…...

【新】致远OA从前台XXE到RCE漏洞分析
0x01 前言 致远OA是目前国内最流行的OA系统之一,前几年也曾爆出过多个安全漏洞。致远官方一直对修复漏洞的态度十分积极,目前能有效利用的致远漏洞已经很少了。 和我们之前分享过的通达OA的漏洞类似,这类主流OA系统现在想要直接一步达到RCE的…...
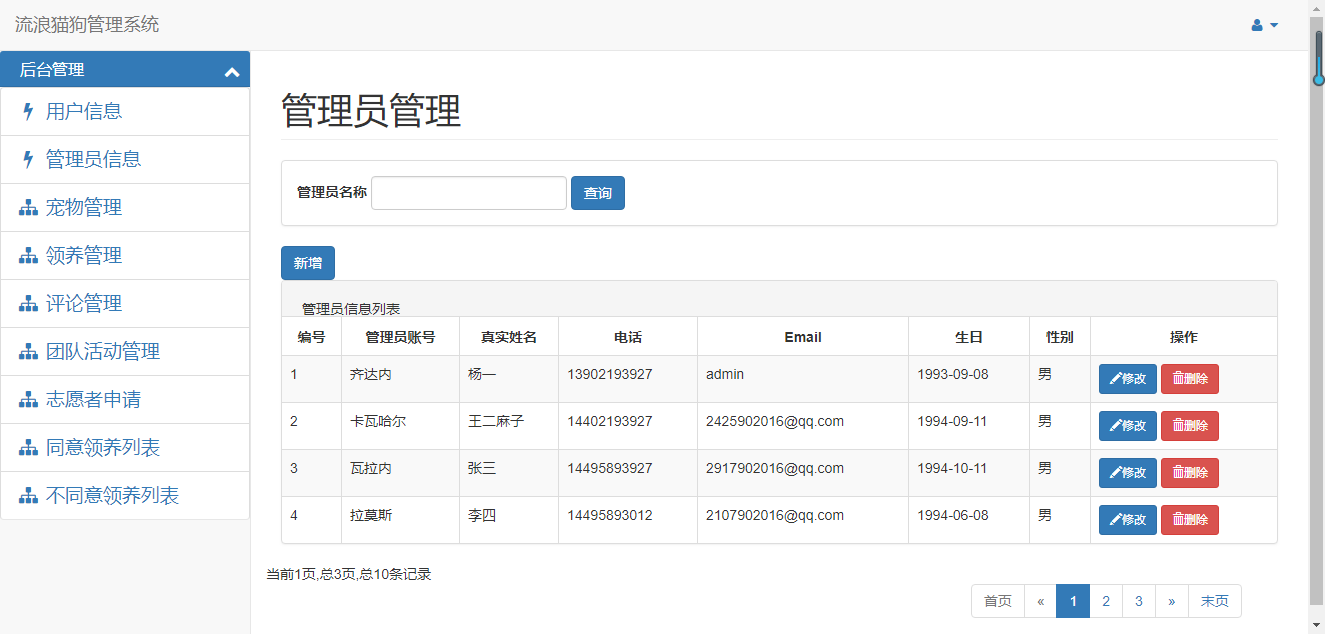
宠物领养系统jsp+servlet+mysql
设计不同用户的操作权限、注册和登录方法。 管理员可以在管理员管理、用户管理、宠物管理、评论管理、团队活动管理、志愿者的申请等等模块中进行查询、添加、删除、修改。 管理员可以在领养管理中通过领养时间查询所有宠物被领养的信息,修改是否同意领养宠物&#…...

MySQL 数据库安全性练习题
数据库安全性 一、实验目的 (1)熟悉通过MySQL对数据进行安全性控制 二、实验环境 Windows 11 MySQL Navicat 三、实验内容 今有以下两个关系模式: 职工(职工号,姓名,年龄,职务,工…...

如何使用Node.js快速创建HTTP服务器并实现公网访问本地Server
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...
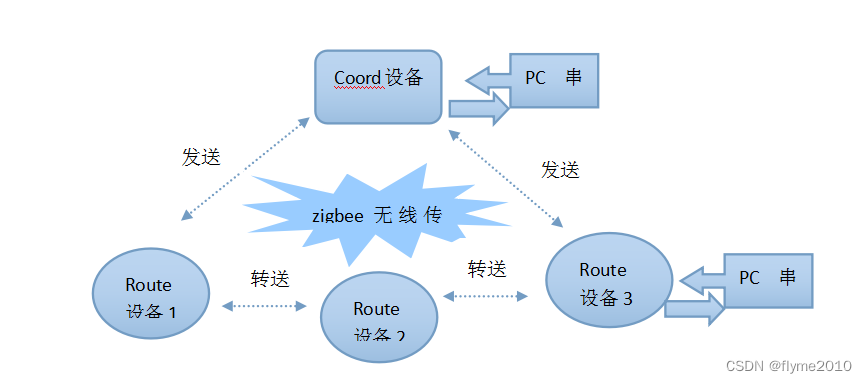
zigbee路灯无线通讯机制
zigbee路灯无线通讯机制 wang20160630 前言 目前路灯上通讯主要有电力载波和无线通讯;各有利弊,众说纷纭;本文不对两种技术进行比较,也不讨论哪种好,毕竟同种通讯模块,有的开发出来稳定,有的…...

asp.net docker-compose添加kafka和redis和zookeeper
docker-compose.yml添加 redis:image: redis:alpinekafka:image: "bitnami/kafka:3.1.1"depends_on:- zookeeperzookeeper:image: "bitnami/zookeeper:3.5.10" docker-compose.override.yml添加 redis:ports:- "6379"kafka:links: - zookeepere…...

2024上海国际人工智能展(CSITF)“创新驱动发展·科技引领未来”
人工智能(Artificial Intelligence,AI)作为当今世界科技发展的关键领域之一,正不断推动着各行各业的创新和变革。作为世界上最大的消费市场之一,中国正在积极努力将AI技术与产业融合并加速推广应用。在这个背景下&…...

汽车标定技术(三)--XCP协议如何支持测量功能
目录 1. 概述 2. 测量方式 -- Poll 3. 测量方式 -- DAQ 3.1 ODT概念模型 3.2 DAQ List概念 3.3 ODT 绝对编号和相对编号 3.4 静态DAQ和动态DAQ模式 (1)静态DAQ (2)动态DAQ 4.小结 1. 概述 在该系列的首篇文章汽车标定技…...

[c++]你最喜爱的stringstream和snprintf性能深入剖析
最近写一个程序中两个差不多的模块,一个使用了snprintf输出中间数据,另一个偷懒使用stringstream。结果你猜怎么着?居然压帧了!!到底是谁拖了性能的后退? 来自阿里云的性能分析实验 我上网一搜࿰…...
windows 用vs创建cmake工程并编译opencv应用项目生成exe流程简述
目录 前言一、安装opencv(1)下载(2)双击安装(3)环境变量和system文件夹设置 二、打开vs创建项目三、编辑cpp,.h,cmakelist.txt文件(1)h文件(2&…...
QML 仪表盘小示例
本次项目已发布在CSDN->GitCode,下载方便,安全,可在我主页进行下载即可,后面的项目和素材都会发布这个平台。 个人主页:https://gitcode.com/user/m0_45463480怎么下载:在项目中点击克隆,windows:zip linux:tar.gz tar # .pro TEMPLATE = appTARGET = dialcontrol#…...
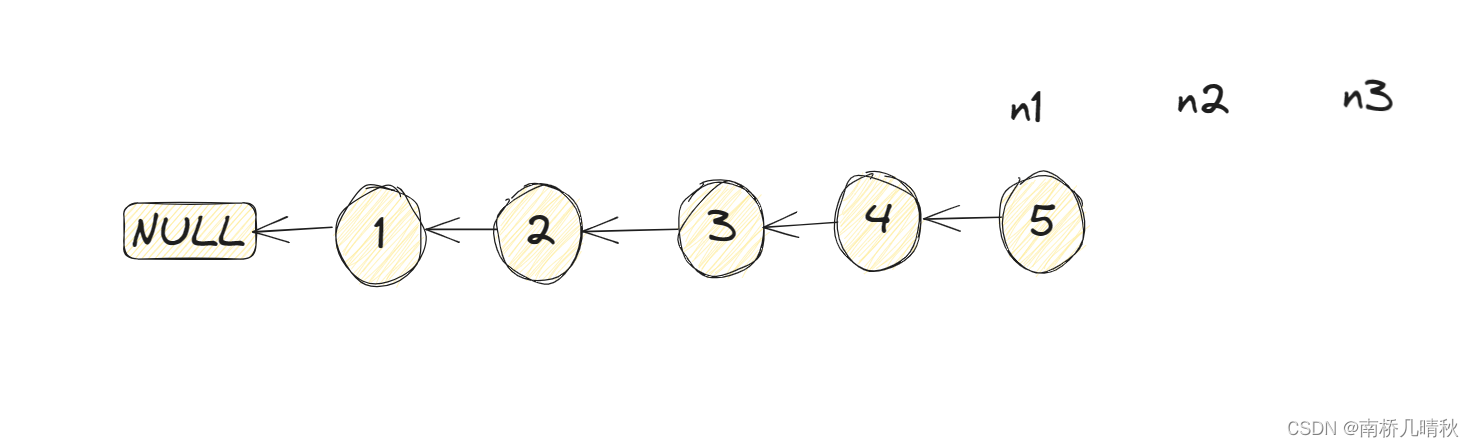
力扣206. 反转链表
题目: 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3:…...
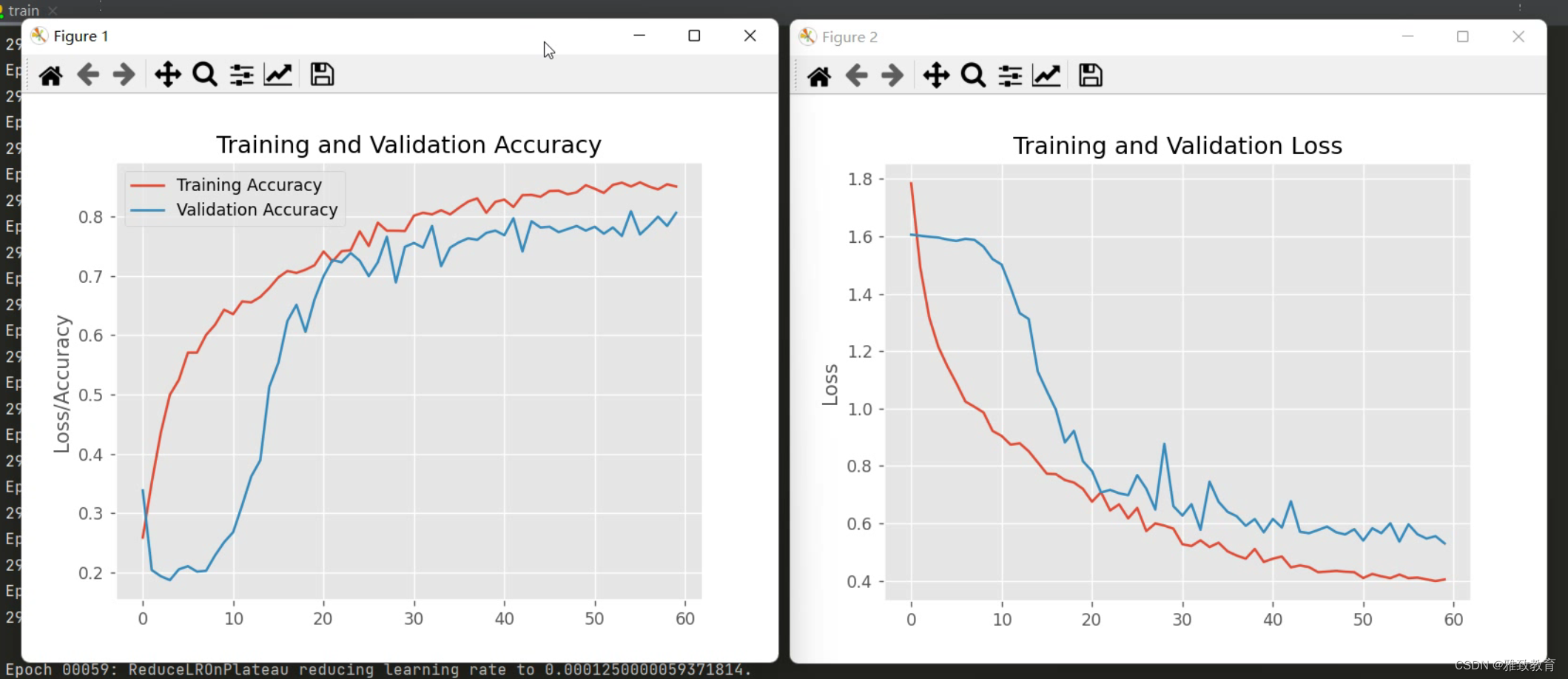
深度学习之基于Tensorflow卷积神经网络花卉识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 深度学习是一种机器学习方法,它通过模拟人脑神经网络的结构和功能来实现对数据的自动分析和学习。卷积神…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
