turtle绘制分形树-第10届蓝桥杯省赛Python真题精选

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第5讲。
turtle绘制分形树,本题是2019年3月24日举行的第10届蓝桥杯青少组Python编程第5题,题目要求使用turtle绘制二叉树和分形树丛。
先来看看题目的要求吧。
一.题目说明
1
题目说明
编程实现:
分形树
步骤 1:
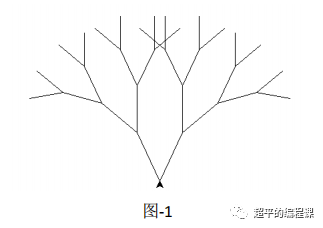
利用 turtle 画出如本题图-1所示的分形树。
具体要求:
1) 树木主干向上生长;
2) 分形层数为4,二叉树;
3) 第一层树枝长度为60,逐层减6;
4) 左右树枝的倾斜角度不限,最终效果与图-1 所示大致相同即可。
5) 必须能看出绘图过程。
将程序命名为“lq00501”。
评判标准:
-
10分:能够画出大致如图中的第一层树枝;
-
30分:能够画出大致如图中的两层以上的树枝,且为二叉树;
-
50分:完全符合题意,即:向上生长,二叉树,层数为4,树枝长度每层递减,能看出绘图过程。
步骤 2:
一.修改步骤1中生成分形树的方法
1) 分形层数改为 4~6 之间的随机数;
2) 第一层树枝长改为 30~60 之间的随机数;
二.绘制分形树丛
1) 在 800X600 的屏幕中绘制分形树丛;
2) 树木数量为 50 棵;
3) 每棵分形树的树根位置为屏幕范围内随机坐标点,树枝允许伸出屏幕窗口外;
4) 以屏幕中心垂直线为分界,位于屏幕左侧的树木向左倾斜,位于屏幕右侧的树木向右倾斜;
5) 绘制过程瞬间完成(即看不到绘画过程)。
整体绘制样例如本题图-2(下面两张图)所示。


将程序命名为“lq00502”。
评判标准:
-
0 分:步骤 1 没有得到满分;
-
10 分:能在画布中画出 50 颗随机位置的树木,即使朝向相同、层数固定;
-
30 分:在 10 分标准的基础上,能画出层数随机、树枝长短随机的分形树;
-
50 分:完全符合题意,即在 30 分标准的基础上,能画出符合题意要求朝向倾斜的分形树,且绘画过程瞬间完成(即看不到绘画过程)。
二.思路分析
这是一道海龟画图的题目,涉及到的知识点主要包括turtle的灵活运用以及递归算法。
根据题目的要求和描述,采取逐步分解的思维,我们可以将本题分成如下四步:
-
绘制层数为1的二叉树
-
绘制层数为4的二叉树
-
层数和树枝长度随机
-
绘制分形树丛
首先来看第一步,这一步最简单,只需要绘制两个树枝即可,如图所示:

绘制方法也比较简单,需要注意的是,小海龟的初始方向向上,在绘制完毕后,小海龟必须恢复到原始状态,包括位置和方向。
对应的代码大致如下:

接下来我们考虑第二步,绘制层数为4的二叉树。聪明的你应该发现了这里面的规律,每一棵独立的二叉树的画法都是一样的。
所不同的只是位置和大小,这不就是典型的递归吗。

因此,我们可以定义一个方递归函数,其参数为层数和树枝长度,然后分别在两棵子树的顶端调用自己,调用时需要改变层数和长度。
对于很多同学来说,递归不太好理解,其实你只需记住两点:
1). 在什么时候需要调用递归函数;
2). 调用时参数应该如何变化;
其它的交给递归函数就好了,它会帮我们完成具体的绘制过程的。
第三步相对比较简单,只需生成两个随机数,作为参数进行调用即可。
第四步,绘制分形树丛,这是本题的难点。仔细观察绘制样例,可以发现树丛中的树分为两种,一种是向左倾斜的,一种是向右倾斜的。
而前面绘制的二叉树是对称的,因此需要在此基础上进行调整,其实只需要将角度做一个微调就可以了。
由于有两种不同的倾斜方向,可以定义两个递归函数,分别对应两种不同的二叉树。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们分4步来编写代码:
-
定义递归函数
-
绘制4层二叉树
-
随机层数和长度
-
绘制分形树丛
1. 定义递归函数
根据上面的思路分析,定义递归函数tree()如下:
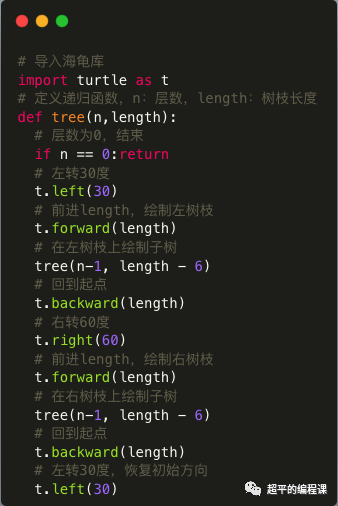
每一步都有详细注释,这里就不再赘述了,强调一点,递推函数一定要有边界条件,也就是出口,本例中的n == 0就是边界条件。如果没有边界条件,那么就会陷入死循环。
2. 绘制4层二叉树
使用组合函数,相对就简单多了,代码如下:

代码比较简单,需要强调的是,关于小海龟的方向,有两种模式,分别是标准模式和logo模式,如图:
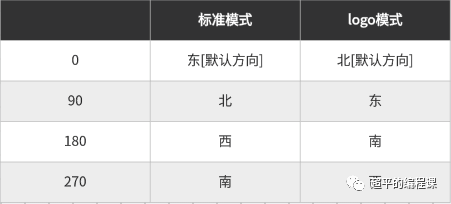
turtle默认使用的是标准模式,在该模式下,默认方向是东(向右)。如果需要小海龟向上,则需要使用seth(90)函数设置。
这样一来,4层结构的二叉树就绘制好了,可以按照题目要求保存为lq00501.py了。
3. 随机层数和长度
这一步,相对比较简单,需要导入随机库,生成两个随机数,分别表示层数和树枝长度,然后调用函数即可,代码如下:
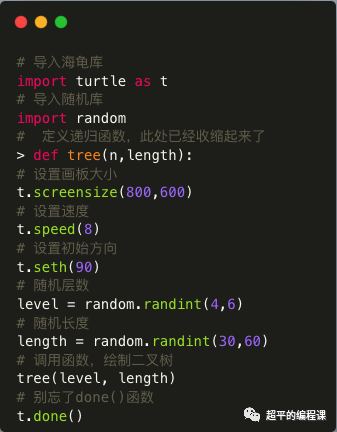
4. 绘制分形树丛
根据前面的思路分析,需要定义两个函数,分别实现两边倾斜的二叉树。
先定义左边倾斜的二叉树,代码如下;
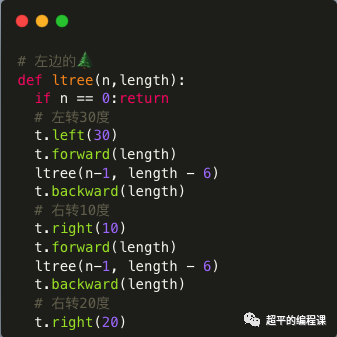
其次是右边倾斜的二叉树,代码如下:

两段代码基本一样,唯一不同的是方向,一个朝左倾斜,一个朝右倾斜。
以左二叉树为例,先左转30度,绘制左边的树,然后右转10度,绘制右边的树,再退回到起点之后再右转20度,确保恢复到初始状态。
有了这两个函数,接下来就可以绘制树丛了,一共是50棵,需要用到循环,同时使用随机数生成随机坐标,再根据坐标,绘制相应的二叉树即可。
对应的代码如下:
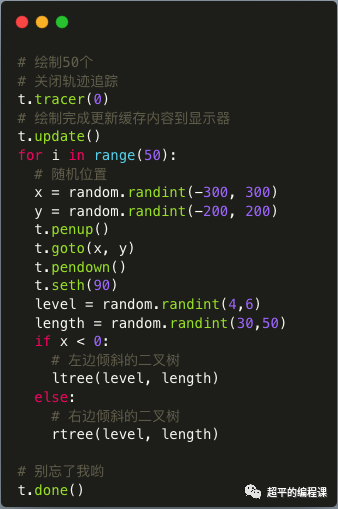
简要说明两点:
1). 题目要求瞬间完成,此时就不能speed()方法了,需要使用t.tracer(0)和t.update()配合使用;
2). 移动小海龟时,需要抬笔,避免多余的直线;
运行程序,执行结果如下:
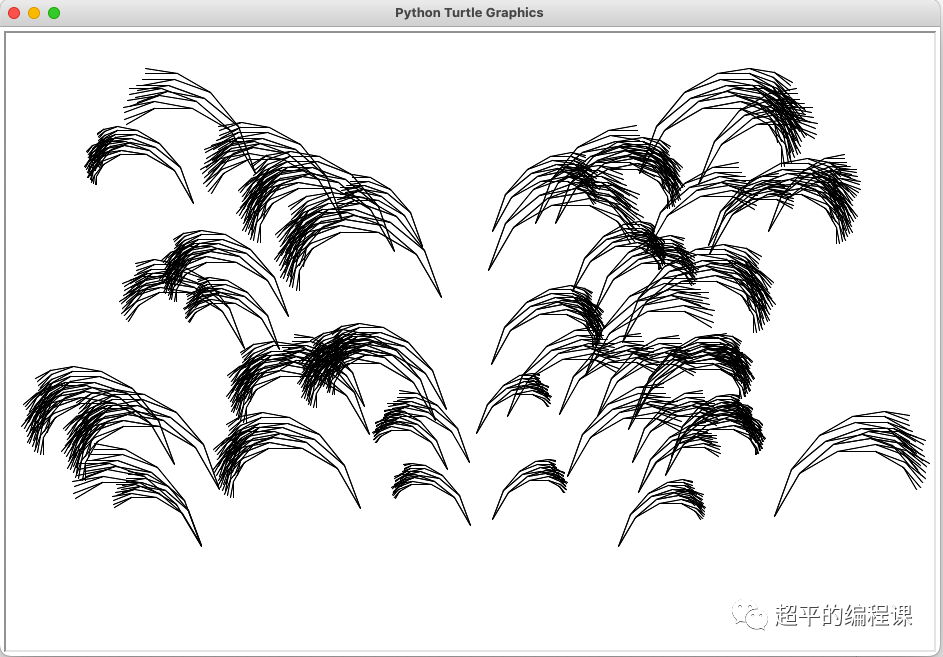
按照题目要求, 将第3步和第4步的代码保存为lq00502就可以了。
怎么样,效果还不错吧, 至此,整个程序就全部完成了。
四.总结与思考
本题是中级组编程部分第5题,分数为100分,代码在50行左右,涉及到的知识点包括:
-
循环语句,主要是for...in循环;
-
Turtle的灵活运用;
-
函数的定义及使用;
-
随机数的使用;
-
坐标知识;
-
递归算法;
题目难度较大,主要体现在两个方面,一是绘制多层的二叉树,二是绘制分形树丛。提到二叉树,就离不开递归算法,递归算法的特点就是代码比较简洁,但是理解起来有些困难。
关于递归,超平老师后面会出专题来进行详细讲解,这里就不再单独说了,先学会简单的应用就可以了。
超平老师给你留一个思考题,除了本题给出的树的效果,还有各种不同的效果,比如:

你知道该怎么绘制吗,赶紧动手试试吧。
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
相关文章:

turtle绘制分形树-第10届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第5讲。 turtle绘制分形树&…...

【大厂招聘试题】__硬件工程师_2021年“美团”校招
目录 匹配职位:硬件工程师 1.(多选题)单处理系统中,进程P1,P2,P3处于就绪队列,进程P4,P6处于等待队列,P5正占用处理器运行,以下对接下来的运行合理的分析是( ÿ…...

算法通关村第七关|黄金挑战|迭代实现二叉树的前、中、后序遍历
1.迭代实现前序遍历 public List<Integer> preOrderTraversal(TreeNode root) {List<Integer> res new ArrayList<Integer>();if (root null) {return res;}Deque<TreeNode> stack new LinkedList<TreeNode>();TreeNode node root;while (!…...

了解高防服务器的工作原理
在当今互联网时代,网络安全问题日益突出,各种网络攻击层出不穷。为了保护企业的网络安全,高防服务器应运而生。那么,你是否了解高防服务器的工作原理呢?下面就让我们一起来探索一下。 高防服务器是一种能够有效抵御各种网络攻击的…...

AVL树性质和实现
AVL树 AVL是两名俄罗斯数学家的名字,以此纪念 与二叉搜索树的区别 AVL树在二叉搜索树的基础上增加了新的限制:需要时刻保证每个树中每个结点的左右子树高度之差的绝对值不超过1 因此,当向树中插入新结点后,即可降低树的高度&…...

出口贸易媒体发稿推广6个技巧提升品牌知名度-华媒舍
1. 出口贸易媒体介绍 出口贸易媒体是指专注于报道国际贸易、跨境业务和进出口市场的媒体平台。这些媒体对于企业发展来说至关重要,可以帮助品牌扩大影响力、提升知名度,促进商业合作。下面介绍6个出口贸易媒体发稿推广技巧,帮助企业更好地利…...
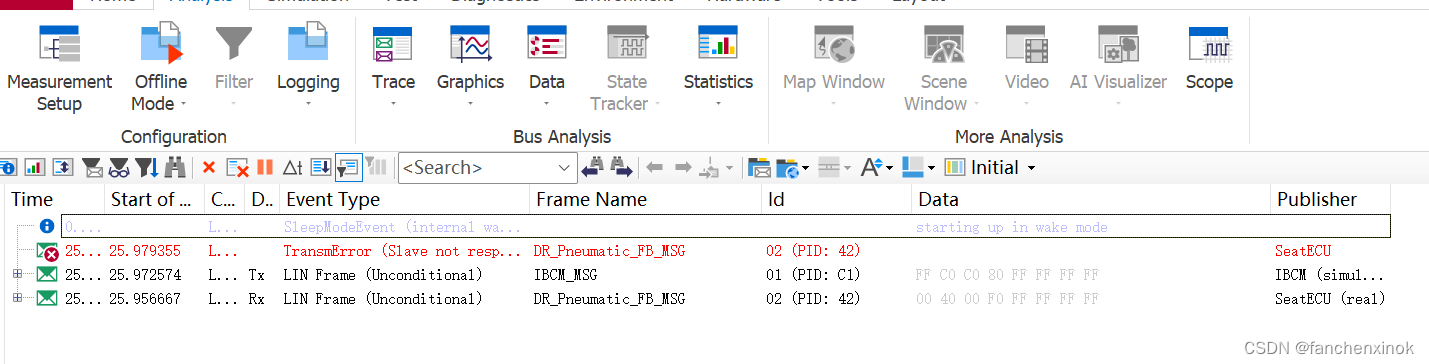
学习笔记:CANOE模拟LIN主节点和实际从节点进行通信测试
先写点感想,在LIN开发阶段,我一般用图莫斯USB工具来进行模拟主机节点发送数据。后来公司买了CANOE工具就边学习边搭建了LIN的测试工程,网上的资料真的很少,主要是靠自己一点点摸索前进,总算入门。几个月后的今天&#…...
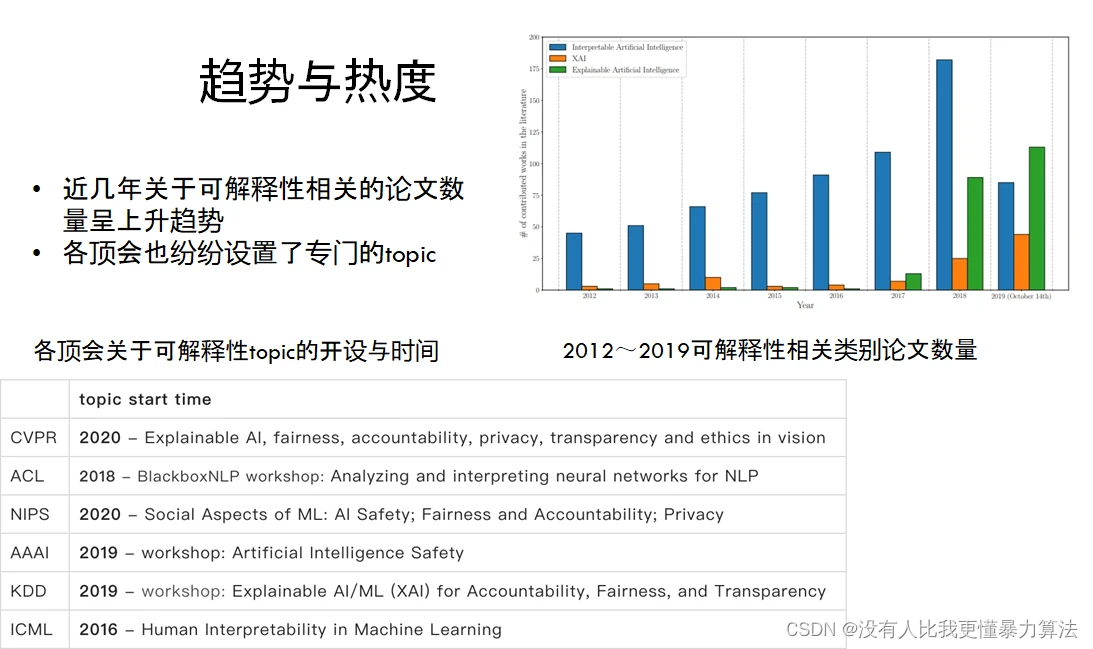
模型可解释性
模型可解释性 前言导读Background1、为什么需要可解释性?2、诞生背景3、研究现状4、常见的模型可解释性方法4.1 基于模型自身的可解释性1)Explanation Generation2)Prototype Network 4.2 基于结果的可解释性 5、应用前景6、面临挑战 前言导读…...

Django初窥门径-自定义用户模型
前言 自定义用户模型在Django应用中是一个重要的话题,它涉及到如何根据您的项目需求以及特定的用户身份验证和授权需求来调整用户模型。在以下前言中,我将讲述为什么自定义用户模型是如此重要以及其潜在的优势: 随着Web应用的不断发展&…...
微信小程序文件上传wx.uploadFile
网页版查看了一下负载要求是这样 wx.uploadFile({url: ${wx.getStorageSync(apiUrl)}//sysFileInfo/upload?token${wx.getStorageSync(token)}, // 仅为示例,非真实的接口地址filePath: files[0].url,name: file,formData: {secretFlag: Y },success: (res) > {…...
支持内录系统声音的Mac录屏软件Omi Recorder
Screen Recorder by Omi是一款功能强大的屏幕录制应用程序。它可用于在Windows和Mac计算机上捕获屏幕,以便进行演示、教程、游戏录制、视频编辑等各种用途。 以下是该应用程序的一些主要特点: 支持高清录制:Omi Screen Recorder可以以高达6…...
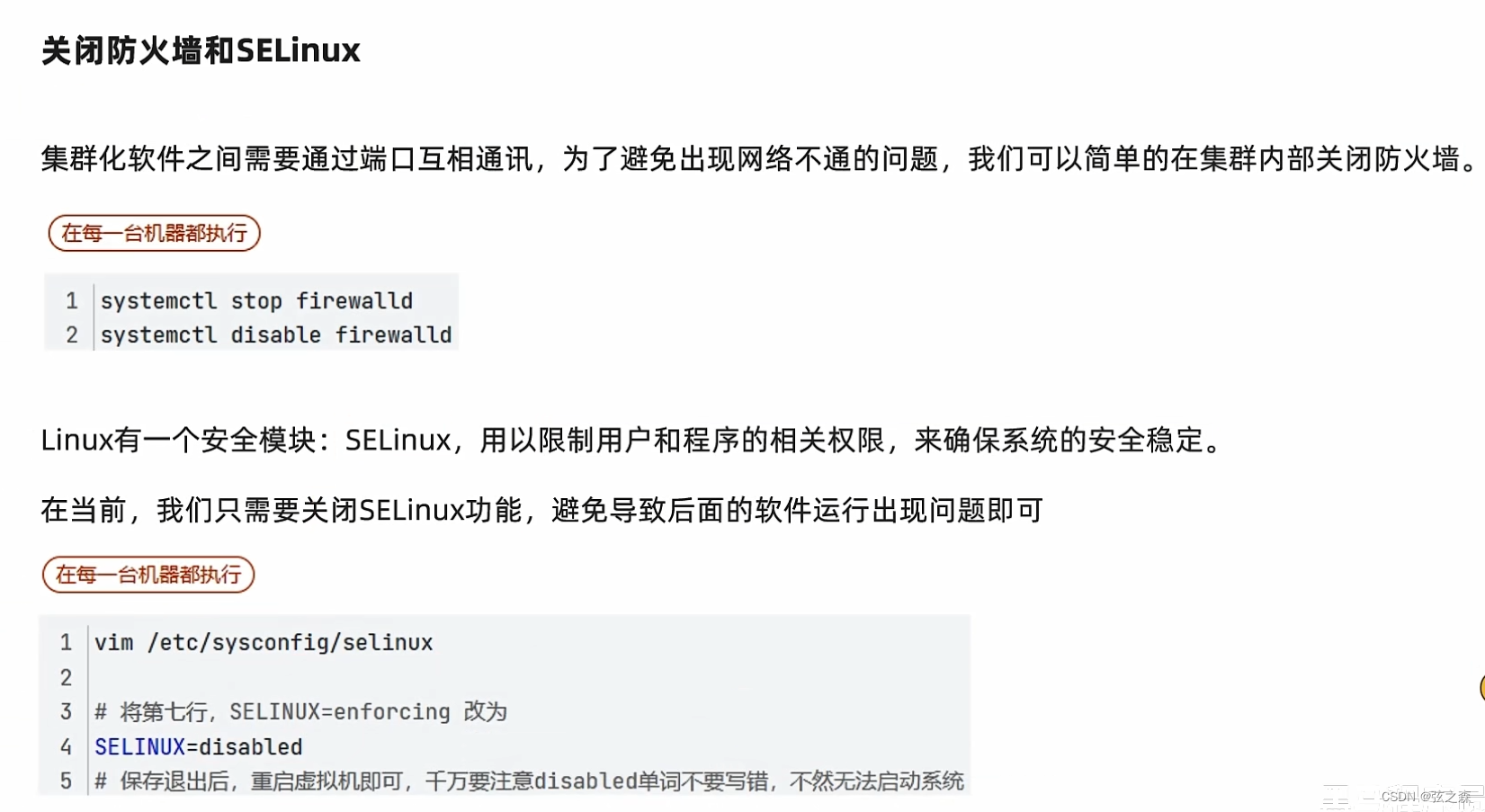
一、Hadoop初始化配置(final+ubuntu保姆级教程)
1、配置虚拟机 三台虚拟机,分别为node1、node2、node3,内存分别为4G、2G、2G,现存最好为(>40G),如下: 2、修改主机名 分别打开三台虚拟机,root用户输入一下命令: no…...

Linux常用的包管理工具
Linux系统中有两个常用的包管理工具,分别是yum和apt。 1. yum命令 yum是Red Hat公司开发的一种包管理器,主要用于安装、更新、卸载和管理RPM包。它是基于RPM包管理系统的,可以自动解决软件包依赖关系问题。 常用yum命令: - 安…...
python随机生成指定长度的字符串
需求:随机生成一个指定长度的字符串(数字和小写字母) 涉及到的python知识点 (1)python模块包:random random.choice(sequence):从指定的序列中获取一个随机元素 random.choice(sequence)从序…...

语音识别接口试用
语音识别结果对比 1.jonatasgrosman/wav2vec2-large-xlsr-53-chinese-zh-cn 啊五包你没有什么问题嗓局问的这老受刚来指伯间我想就了解其二联地完觉全没问题犹该奖姐家女标要等到老师主动据奖定练择因位我主要奖的是耶号联接最长加展们如果说宁士比到六点级到一到另年级的家长…...

Java的数组使用
数组的定义: package The_First_Stage.The_beginner_level_Java_SE.Arrawy;/*** 数组的作用:用来存储相同类型的数据* 以int类型数据为案例:数组用来存储int类型数据* 1》声明定义数组* int【】 arr 定义一个int类型的数组,名字…...

基于STC15单片机温度光照蓝牙传输-proteus仿真-源程序
一、系统方案 本设计采用STC15单片机作为主控器,液晶1602显示,DS18B20采集温度,光敏电阻采集光照、按键设置温度上下限,测量温度小于下限,启动加热,测量温度大于上限,启动降温。 二、硬件设计 …...

Jmter接口网站压力测试工具
首先下载Jmeter 官方地址:Apache JMeter - Apache JMeter™ 安装Jmeter 把下载的文件进行解压,产生如下目录: 打开bin文件夹下的jmeter.bat文件及进入程序的主界面窗体jmeter.log是日志文件。 主意:需要配置java环境。 jmter创…...

7.2 创建和销毁条件变量
方法 pthread_cond_init(condition, attr) pthread_cond_destroy(condition) pthread_condattr_init(attr) pthread_condattr_destroy(attr) 用法 条件变量的类型为pthread_cond_t,必须在使用之前初始化。有如下两种方法来初始化条件变量: 声明时初…...

九凌网络:谷歌seo优化和外贸建站的五大优势
九凌网络是专注于谷歌SEO和外贸网站建设技术研发的技术型公司。九凌网络为外贸企业提供优质的外贸建站和谷歌优化服务,目前全国合作过的外贸企业超过8000家,覆盖全国12个省,超过60个地级市,在运营的谷歌seo优化客户300多家&#x…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
