当前位置： 首页 > news >正文

关于SSP3D复现

news 2026/2/8 20:46:19

关于SSP3D复现的问题

准备工作

  1. 下载Xshell和XFTP：家校免费版下载链接
  2. 连接服务器（可能需要与服务器处在相同网络下）
  3. GitHub上下载源码：SSP3D
    左上角新建会话，输入名称和主机
    新建会话
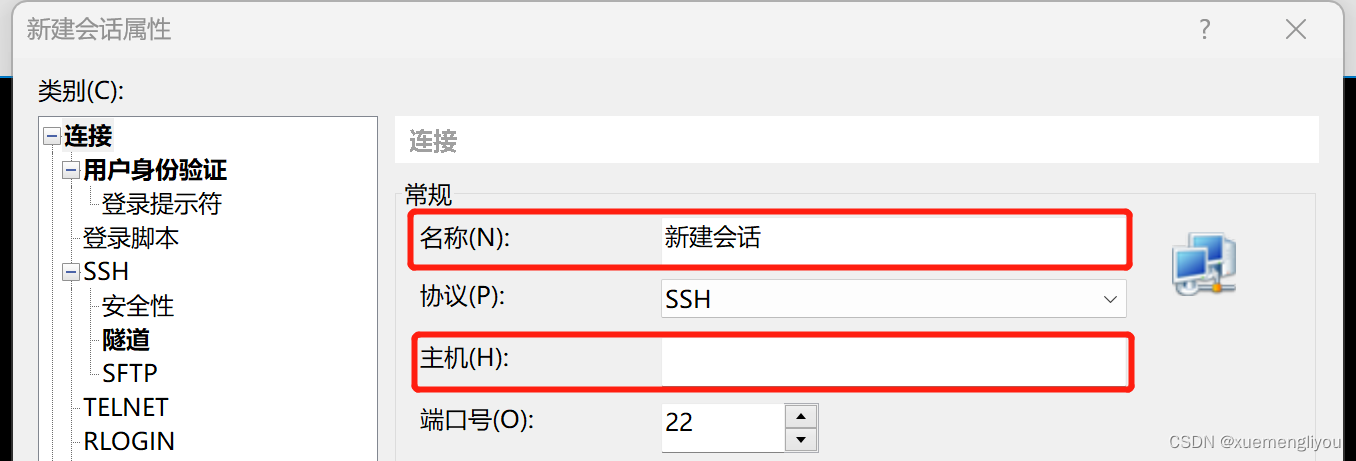
    点击左侧菜单“用户身份验证”，输入用户名和密码
    用户身份验证

数据集

略

安装依赖包

不要直接装requirement.txt里的所有包！
正常运行代码，缺少哪个conda install 哪个
出现问题可以优先尝试切换源
尽量不要使用pip install，改用conda install

运行python runner_shapenet.py

  • 激活conda环境：conda activate fz
  • 切换到代码目录：cd /media/deepsea/DATA/fz/SSP3D
  • 创建虚拟屏幕：screen -S xxx（恢复： screen -r xxx，如果不能恢复：先screen -d xxx 再 screen -r xxx）
  • 运行代码：python runner_shapenet.py

报错：OSError: [Errno 22] Invalid argument:'. \\output'
报错

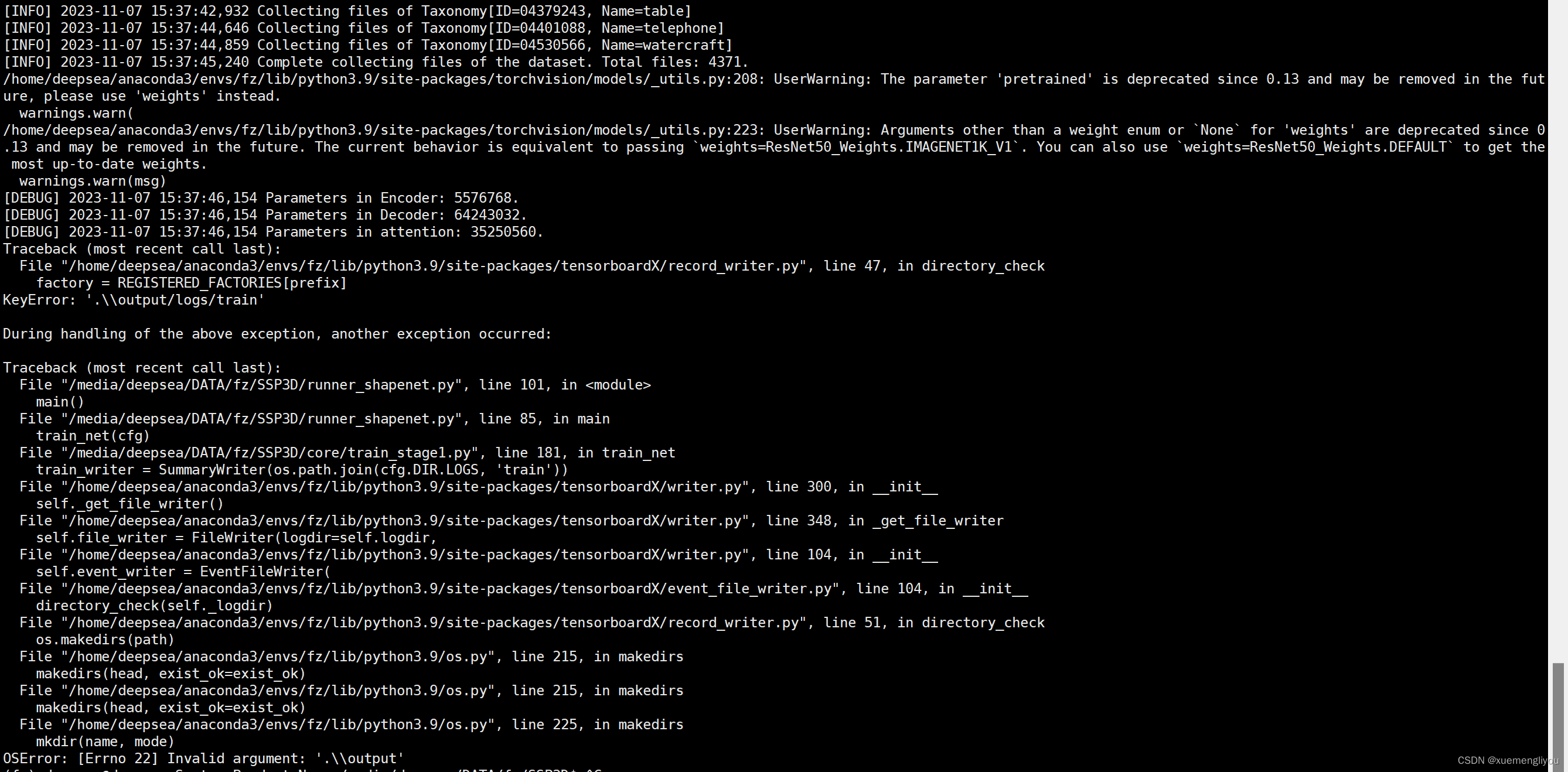
由下到上逐个寻找排查问题（不要从上到下看！）
发现core/train_stage1.py里的train_writer调用路径出现问题，往上看，python runner_shapenet.py里的train net(cfg)，因此找到config.py里，__C.DIR.OUT_PATH = './output'，本地没有问题，但服务器中该行代码为双斜杠，修改回去即可正确运行。

找bug的时候，本地找不到就去服务器找！

相关文章：

关于SSP3D复现

关于SSP3D复现的问题 准备工作 下载Xshell和XFTP：家校免费版下载链接连接服务器（可能需要与服务器处在相同网络下）GitHub上下载源码：SSP3D 左上角新建会话，输入名称和主机 点击左侧菜单“用户身份验证”&#xff0c…...

编程日记 2023/11/8 1:00:39

在直播系统中使用RTSP协议传递视频

目录 概述 1、环境准备 2、拉流URL地址 3、导播软件取流 （1）OBS中拉取RTSP流 （2）芯象中拉取RTSP流 （3）vMix中拉取RTSP流 写在最后 概述 提到RTSP协议，很容易想到RTMP协议，它…...

编程日记 2023/11/8 0:59:38

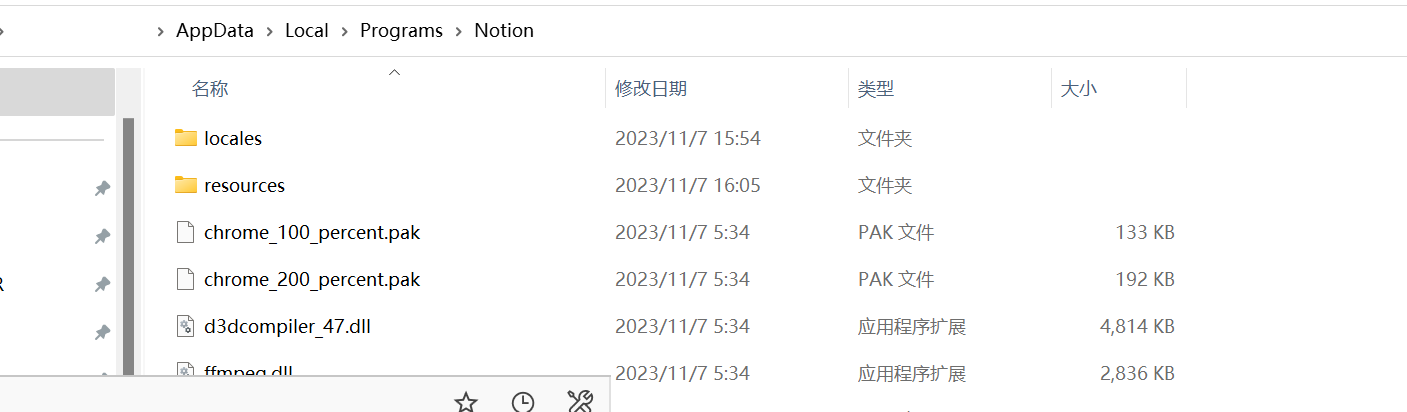
Notion汉化

Notion真无语，汉化版都没有。真的无力吐槽。 2023.11.7汉化经历 教程链接：github Reamd7/notion-zh_CN at 2.4.20-handmade (github.com) 网页版： 油猴下载插件。 Notion中文汉化 浏览器插件下载 windows： github realse 这…...

编程日记 2023/11/8 0:58:37

echarts有背景的柱状图，鼠标滑过提示信息都是展示背景柱状图的值

// 上一篇文章介绍了如何实现有背景的柱状图，现在又遇到一个问题，鼠标滑过柱子，提示信息是背景柱子的值，解决方案，自定义tooltip的formatter，上代码tooltip: {//鼠标悬浮提示数据formatter: function (para…...

编程日记 2023/11/8 0:57:35

华为防火墙基本原理工作方法总结

防火墙只会对tcp首包syn建立会话表，其它丢掉，如synack，ack udp直接建立会话表 icmp只对首包请求包建立会话表，其它包，如应答的不会建立直接丢掉 防火墙状态查看： rule name trust_untrust source-zone tru…...

编程日记 2023/11/8 0:56:33

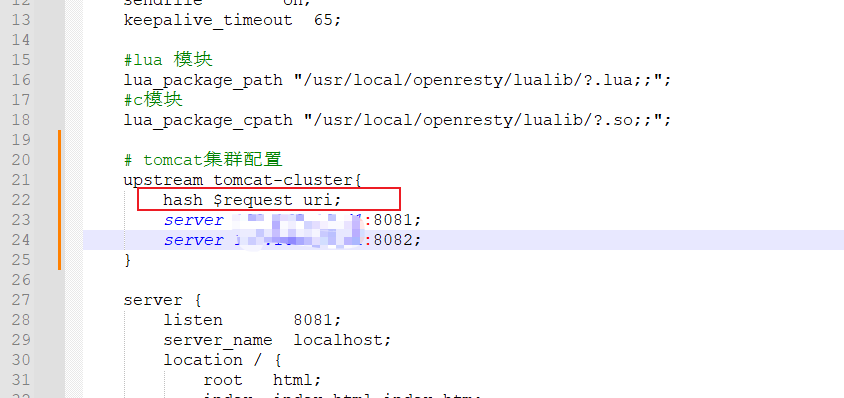
Spring Cloud之多级缓存

目录 传统缓存 多级缓存 JVM进程缓存 Caffeine 缓存驱逐策略 实现进程缓存 常用Lua语法 数据类型 变量声明 循环使用 定义函数 条件控制 安装OpenResty 实现Nginx业务逻辑编写 请求参数解析 实现lua访问tomcat JSON的序列化和反序列化 Tomcat的集群负载均衡 …...

编程日记 2023/11/8 0:55:33

融云荣登「2023 年度 PaaS 企业排行榜」

11 月 2 日，中国科学院旗下《互联网周刊》颁布“2023 年度 PaaS 企业排行榜”，融云荣登榜单。关注【融云全球互联网通信云】了解更多 根据中国信息通信研究院《云计算白皮书 2023》：2022 年，PaaS 增长强势，总收入 342 …...

编程日记 2023/11/8 0:54:32

YOLOv8轻量化模型：模型轻量化设计 | 轻量级可重参化EfficientRep| 来自YOLOv6思想

💡💡💡本文解决什么问题：在几乎不保证精度下降的前提下，轻量级模型创新设计 EfficientRep 在关键点检测任务中 | GFLOPs从9.6降低至8.5， mAP50从0.921下降至0.912，mAP50-95从0.697提升至0.779 YOLO轻量化模型专栏：http://t.csdnimg.cn/AeaEF 1.YOLOv6介绍 论文…...

编程日记 2023/11/8 0:52:30

【JavaSE】基础笔记 - 类和对象（下）

目录 1、this引用 1.1、为什么要有this引用 1.2、什么是this引用 1.3、 this引用的特性 2、 对象的构造及初始化 2.1、 如何初始化对象 2.2、构造方法 2.2.1、概念 2.2.2、特性 2.3、默认初始化 2.4、就地初始化 上篇：【JavaSE】基础笔记 - 类和对象&#…...

编程日记 2023/11/8 0:51:29

浅析刚入门Python初学者的注意事项

文章目录 一、注意你的Python版本1.print()函数2.raw_input()与input()3.比较符号&#xff0c;使用!替换<>4.repr函数5.exec()函数 二、新手常遇到的问题1、如何写多行程序&#xff1f;2、如何执行.py文件&#xff1f;3、and&#xff0c;or&#xff0c;not4、True和False…...

编程日记 2023/11/8 0:50:28

2023NOIP A层联测26 总结

T1 求 ∑ i 1 n ∑ j i n ( ⨁ k i j a k ) 2 \sum\limits_{i1}^n\sum\limits_{ji}^n\left(\bigoplus\limits_{ki}^{j}a_k\right)^2 i1∑n​ji∑n​(ki⨁j​ak​)2&#xff0c; n , a i ≤ 2 1 0 5 n,a_i\le2\times10^5 n,ai​≤2105。先转成前缀和&#xff0c;然后就没思…...

编程日记 2023/11/8 0:49:27

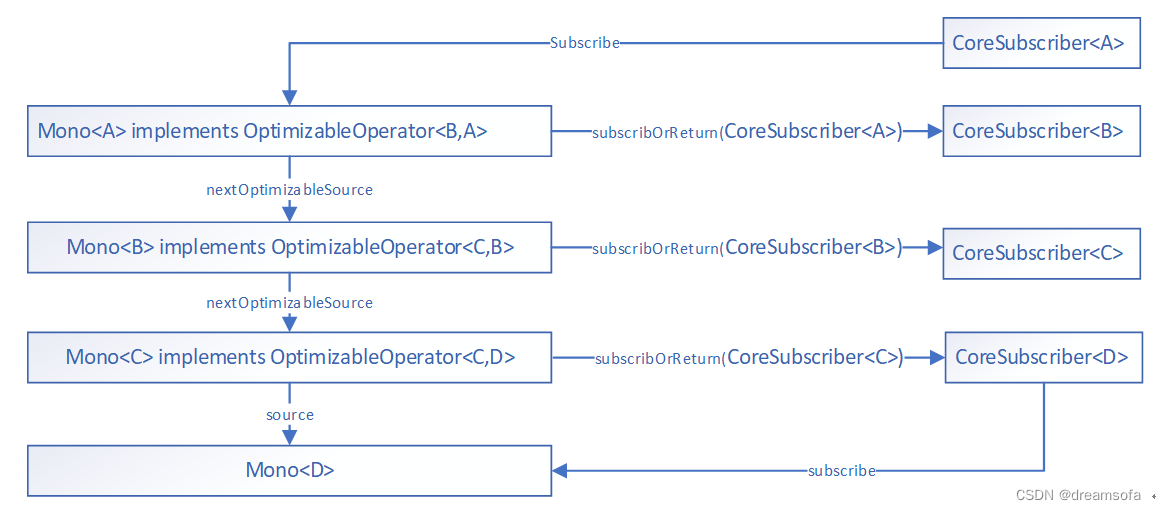
响应式编程-Project Reactor Mono 介绍

响应式编程-Project Reactor Mono 介绍 本文以Mono的角度来介绍Reactor编程&#xff0c;Flux的使用同理。 初体验 Web应用 controller 方法在Spring webmvc 和 Spring webFlux下Controller方法实现示例如下&#xff1a; Spring webmvc: GetMapping("/test1") …...

编程日记 2023/11/8 0:48:26

R语言实操记录——导出高清图片（矢量图）

R语言 R语言实操记录——导出高清图片&#xff08;矢量图&#xff09; 文章目录 R语言一、起因&#xff08;闲聊&#xff0c;可跳过&#xff09;二、如何在R中导出高清图片&#xff08;矢量图&#xff09;2.1、保存为EPS图片格式后转AI编辑2.2、保存为PDF格式&#xff08;推荐…...

编程日记 2023/11/8 0:47:25

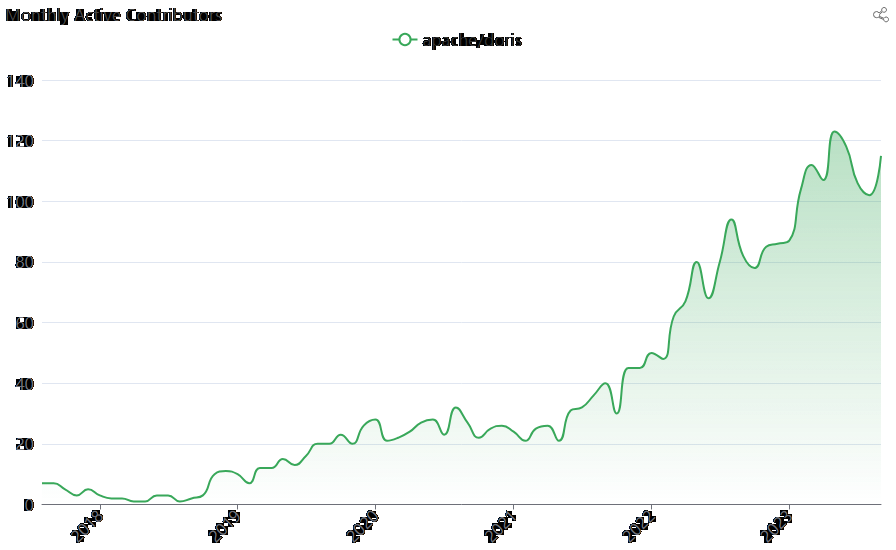
Apache Doris 开源最顶级基于MPP架构的高性能实时分析数据库

背景介绍 Apache Doris是一个基于MPP架构的易于使用&#xff0c;高性能和实时的分析数据库&#xff0c;以其极高的速度和易用性而闻名。海量数据下返回查询结果仅需亚秒级响应时间&#xff0c;不仅可以支持高并发点查询场景&#xff0c;还可以支持高通量复杂分析场景。 这些都…...

编程日记 2023/11/8 0:46:24

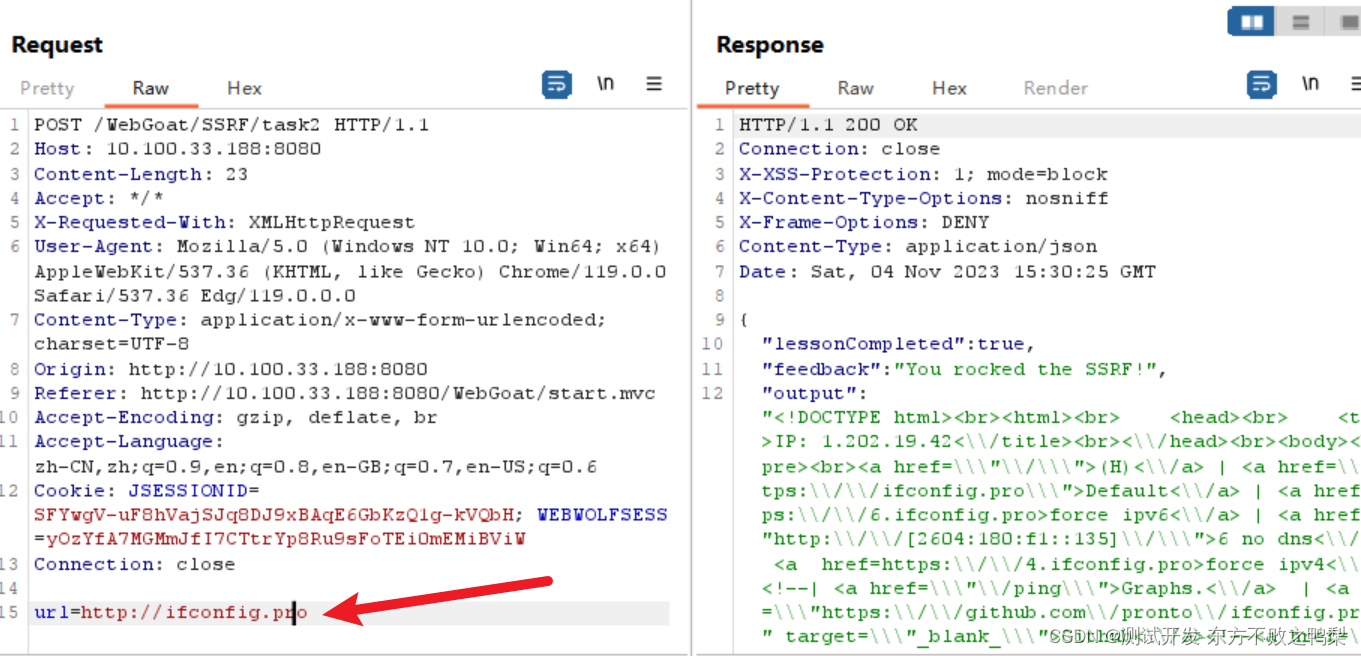
webgoat-Request Forgeries 请求伪造

(A8:2013) Request Forgeries Cross-Site Request Forgeries 跨站请求伪造&#xff0c;又称一键攻击或会话骑乘&#xff0c;简称CSRF &#xff08;有时发音为 sea-surf&#xff09;或 XSRF&#xff0c;是一种恶意利用网站&#xff0c;其中传输未经授权的命令 来自网站信任的用…...

编程日记 2023/11/8 0:44:22

【flask跨域问题】解决它

大概7-8年前&#xff0c;前后端还没开始分离或者刚开始分离的之前&#xff0c;跨域问题很多。 后来我就没在遇到过了&#xff0c;这次做一个小项目&#xff0c;又遇到了&#xff0c;记录下。 现在前端的脚手架都自己能解决了。 1. 跨域 是因为出于浏览器的同源策略限制。同源…...

编程日记 2023/11/8 0:43:21

虚幻引擎:如何在工程里面添加插件

1.在自己的项目中安装插件 在content目录下创建一个Plugins的文件,将插件文件放进去即可 2.在软件上安装,这样所有创建的项目都会带有此插件 将插件放在自己软件的这个目录下就好了...

编程日记 2023/11/8 0:42:20

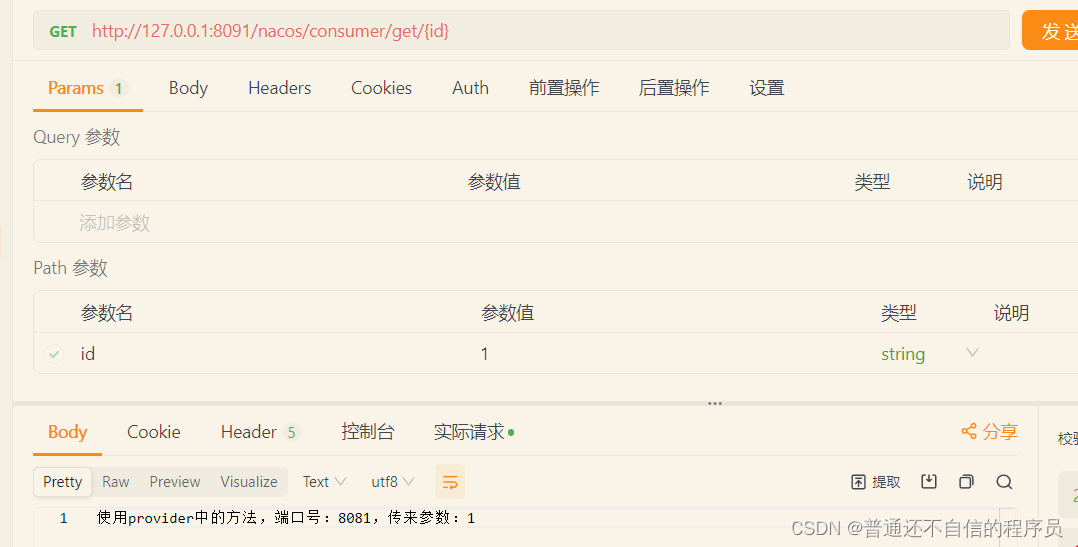
SpringCloud Alibaba 【四】Openfeign

Openfeign配置与使用 前言介绍openfeign使用openfeign导入依赖启动类正式使用测试结果 前言 在springcloud中消费者项目需要调用提供者项目的接口&#xff0c;一开始用的是RestTemplate中的方法。但是RestTemplate进行远程调用时&#xff0c;直接调用controller层的接口&#…...

编程日记 2023/11/8 0:39:18

语音信号的线性预测分析、合成及MATLAB编程设计实现

需要的基础&#xff1a;AR模型、列文森-杜宾递推法 推荐阅读&#xff1a; 基于线性预测的语音编码原理解析 基于线性预测的语音编码原理解析 这篇文章和上一篇类似 语音信号的线性预测分析及其Matlab源码 这篇文章是要付费看的&#xff0c;但是他能预览的那部分写的确实好 语…...

编程日记 2023/11/8 0:38:17

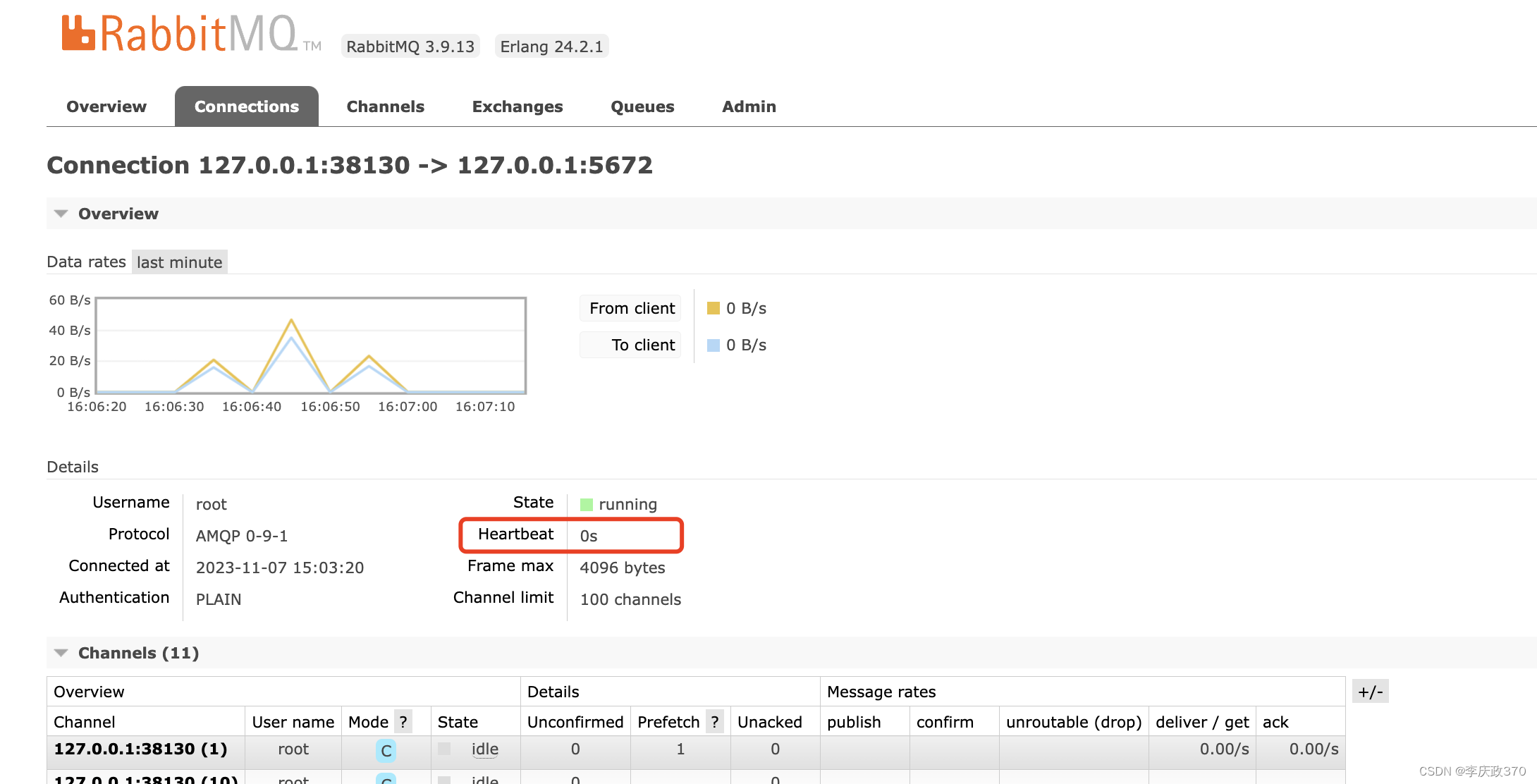
rabbitMQ rascal/amqplib报错 Error: Unexpected close 排查

以下是一些可能导致此 RabbitMQ 客户端或任何其他 RabbitMQ 客户端中的套接字读取或写入失败的常见场景 1.错过&#xff08;客户端&#xff09;心跳 第一个常见原因是RabbitMQ 检测到心跳丢失。发生这种情况时&#xff0c;RabbitMQ 将添加一个有关它的日志条目&#xff0c;然…...

编程日记 2023/11/8 0:37:15

龙虎榜——20250610

上证指数放量收阴线&#xff0c;个股多数下跌&#xff0c;盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型&#xff0c;指数短线有调整的需求&#xff0c;大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的&#xff1a;御银股份、雄帝科技 驱动…...

编程新知 2026/2/8 15:03:06

MMaDA: Multimodal Large Diffusion Language Models

CODE &#xff1a; https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA&#xff0c;它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构&#xf…...

编程新知 2026/2/3 15:24:36

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2026/2/7 10:59:19

Spring Boot面试题精选汇总

&#x1f91f;致敬读者 &#x1f7e9;感谢阅读&#x1f7e6;笑口常开&#x1f7ea;生日快乐⬛早点睡觉 &#x1f4d8;博主相关 &#x1f7e7;博主信息&#x1f7e8;博客首页&#x1f7eb;专栏推荐&#x1f7e5;活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

编程新知 2025/9/24 23:08:17

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)

文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

编程新知 2026/1/31 23:44:39

Netty从入门到进阶（二）

二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架&#xff0c;用于…...

编程新知 2026/1/26 5:44:16

AI+无人机如何守护濒危物种？YOLOv8实现95%精准识别

【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而&#xff0c;传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案&#xff0c;能够实现大范围覆盖并远程采集数据。尽管具备这些优势&#xf…...

编程新知 2026/1/26 12:50:00

站群服务器的应用场景都有哪些？

站群服务器主要是为了多个网站的托管和管理所设计的&#xff0c;可以通过集中管理和高效资源的分配&#xff0c;来支持多个独立的网站同时运行&#xff0c;让每一个网站都可以分配到独立的IP地址&#xff0c;避免出现IP关联的风险&#xff0c;用户还可以通过控制面板进行管理功…...

编程新知 2025/9/1 19:01:24

Qemu arm操作系统开发环境

使用qemu虚拟arm硬件比较合适。 步骤如下&#xff1a; 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载&#xff0c;下载地址&#xff1a;https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

编程新知 2026/1/31 9:18:40

适应性Java用于现代 API：REST、GraphQL 和事件驱动

在快速发展的软件开发领域&#xff0c;REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名&#xff0c;不断适应这些现代范式的需求。随着不断发展的生态系统&#xff0c;Java 在现代 API 方…...

编程新知 2025/11/10 19:07:59