【机器学习】六、概率图模型
今天我们对概率图模型(Probabilistic Graphical Model,PGM)做一个总结。
模型表示
概率图模型,是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型。
它提出的背景是为了更好研究复杂联合概率分布的数据特征,假设一些变量的条件独立性,由此我们把概率图模型分为有向图和无向图,并且介绍了它们的模型表示、条件独立性。
有向图模型又称贝叶斯网络或信念网络,其联合概率分布可以分解为每个随机变量Xk的局部条件概率的乘积形式:
贝叶斯网络的条件独立性体现在三种形式:tail-to-tail,head-to-tail,head-to-head。
无向图模型又称马尔科夫随机场或马尔科夫网络,它的联合概率分布由Hammersley Clifford定理保证,能够因子分解为定义在最大团上的正函数的乘积:
马尔科夫随机场的条件独立性体现在局部马尔可夫性、全局马尔可夫性和成对马尔可夫性,他们是相互等价的:
接着我们介绍了判断变量条件独立性的方法——D分离,最后我们得到更一般的算法来确定以下形式之一的独立性问题:
给定Z,X和Y是否条件独立
X和Y边际独立吗
文章链接:
概率图模型(模型表示)
概率图模型(D分离)
模型推断
概率图模型只是为了简便研究模型方便而提出的工具,通常我们把得到联合概率分布参数的过程称为Learning问题,得到参数后,最终要进行推断,称为Inference问题,一般情况下,推断问题分为精确推断和近似推断。
精确推断有变量消除法(VE)和信念传播法(BP)。变量消除法的思想,它的核心是每次对一个变量求积分。
VE算法存在很明显的两个缺点:计算步骤无法存储;消除的最优次序是一个NP-hard问题。因此要对此算法进行改进,得到信念传播算法(BP),该算法的流程主要有三步:
step1:任取⼀个节点 作为根节点
step2:对这个根节点的邻居中的每⼀个节点,收集信息
step3:对根节点的邻居,分发信息
近似推断又分为确定性近似和随机性近似。
很多情况,无法用最大似然估计(MLE)直接求得参数,模型由一些不可观测的变量决定,它们无法直接观测,需要引入隐变量来定义它们。通常情况可以用期望最大化(EM算法)求解,它是一种迭代算法,主要思想是把一个难于处理的似然函数最大化问题用一个易于最大化的序列取代,而其极限是原始问题的解。
E步本质是求隐变量z的后验分布p(z|x,θ),想方设法把隐变量z积分掉,M步求似然函数最大值的参数θ。
变分推断(VI)是一种确定性近似方法,它的初始算法是基于平均场假设理论,不过该算法存在两个局限:假设太强,期望的积分可能无法计算。由此对算法改进,得到随机梯度变分推断(SGVI),利用重参数技巧和蒙特卡洛采样得到目标函数的梯度,进而采取梯度下降得到近似解。
随机性近似推断的典型是马尔科夫链蒙特卡洛方法(MCMC),主要思想是通过构建马尔可夫链概率序列,使其收敛到平稳分布p(z)。
蒙特卡洛采样是一种随机模拟方法,核心是求解x的概率分布p(x),以及如何基于概率分布去采集n个样本点。采样的目标是采集到的样本能够代表总体,要满足两点:
样本趋向于高概率的区域
样本之间必须独立
常用的采样方法有概率分布采样(CDF Sampling)、拒绝采样(Rejection Sampling)和重要性采样(Importance Sampling)。
马尔可夫链是一种时间和状态都是离散的随机变量序列,它由状态空间和转移矩阵定义,通常情况我们研究齐次马尔可夫链(未来状态的条件概率分布仅依赖于现在状态)。
平稳分布就是表示在某一个时刻后,分布不再改变。我们通过蚱蜢的例子来深入介绍了平稳分布,它表示了停留在某一状态的概率与从随机采样的前期状态转移到它的概率相同。
但并不是所有马氏链都是平稳分布,所以我们想找到一种构建有平稳分布的马氏链。这就引入了平稳分布的充分条件——细致平衡。
细致平衡条件将平稳分布的序列和⻢尔可夫链的转移矩阵联系在⼀起,把转移矩阵作为提议矩阵(提议函数),通过它可以不断⽣成样本点,就可以完成采样了,这个就是MCMC。主要用到MH算法,面对高维空间的话,用到MH的优化算法——Gibbs采样
文章传送门:
模型推断:VE与BP
EM算法
变分推断(Variational Inference)
MCMC(蒙特卡洛采样)
MCMC(马尔可夫链)
MCMC(MH算法)
具体模型
最简单的图模型是朴素贝叶斯,它是一个强假设:即给定y的情况下,特征之间相互独立:
引⼊单个隐变量后,发展出了高斯混合模型(GMM) :
如果单个隐变量变成序列的隐变量,就得到了动态空间模型(Dynamic Model):
引⼊齐次马尔科夫假设和观测独立假设就有隐马尔科夫模型(HMM),卡尔曼滤波和粒子滤波.
HMM的隐状态假设是离散的,卡尔曼滤波的隐状态假设是连续的,但观测变量服从高斯分布,而粒子滤波是非线性非高斯情况下的动态模型。
为了打破观测独立性,引⼊了⼀种最大熵马尔科夫模型(MEMM),它把最大熵原理与隐马尔科夫模型结合:
为了克服 MEMM 中的局域问题,⼜引⼊了条件随机场(CRF),CRF 是⼀个⽆向图,其中,破坏了⻬次⻢尔可夫假设,如果隐变量是⼀个链式结构,那么⼜叫线性链 CRF。
在⽆向图的基础上,引⼊隐变量得到了玻尔兹曼机,这个图模型的概率密度函数是⼀个指数族分布。对隐变量和观测变量作出⼀定的限制,就得到了受限玻尔兹曼机(RBM)
我们看到,不同的概率图模型对下⾯⼏个特点作出假设:
1. 方向-边的性质
2. 离散/连续/混合-点的性质
3. 条件独立性-边的性质
4. 隐变量-点的性质
5. 指数族-结构特点
此外,我们介绍五种聚类算法:基于质心的K-means算法,基于概率分布的GMM算法,基于密度的DBSCAN算法,基于无向图的谱聚类,以及基于层次聚类的BIRCH算法,其中K-means可以看成GMM的特殊情形。
最后,我们很久前介绍过了贝叶斯线性回归和高斯过程回归(GPR),它也可以看成概率图模型,我们是专门为了介绍一种调参方法而提前介绍这两个模型——贝叶斯优化(BOA),它可以在无法确定函数表达式的前提下,找到函数的最值点。
文章传送门:
高斯混合模型(GMM)
隐马尔可夫模型(背景介绍)
隐马尔可夫模型(前向算法与后向算法)
隐马尔可夫模型(Baum Welch算法与Viterbi算法)
隐马尔可夫模型(模型推断五大问题)
隐马尔可夫模型(算法流程&实例演示)
线性动态系统LDS(别名:卡尔曼滤波)
粒子滤波(Particle Filter)
条件随机场CRF(一)
条件随机场CRF(二)
条件随机场CRF(三)
受限波尔茨曼机(RBM)
高斯网络(GBN与GMN)
聚类算法(K-means)
聚类算法(谱聚类)
聚类算法(BIRCH)
聚类算法(DBSCAN)
聚类算法(相似度与性能度量)
贝叶斯线性回归
高斯过程回归(GPR)
贝叶斯优化
对于上面的概率图模型,我们有部分给出了编程实现,有部分还没有,以后会陆续介绍。目前重点是把原理介绍清楚,对机器学习有个整体把握。熟悉这些工具,加上其原理的思想,在我们工作中灵活应用,希望对亲爱的读者你有用!
我们不久后开始深度学习的内容,再难,我也想你一起学算法!!!
相关文章:
【机器学习】六、概率图模型
今天我们对概率图模型(Probabilistic Graphical Model,PGM)做一个总结。 模型表示 概率图模型,是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型。 它提出的背景是为了更好研究复杂联合概率分布的数据特征&#x…...

机器视觉软件破解的背后是道高一尺,魔高一丈
讲个故事,小明从某购物平台花2000元买了一个C#机器视觉架构,压缩包带加密,卖家让小明先确认收货后给密码。 小明花了3元从另外一家卖家破解开压缩包密码,然后迅速从第一家卖家退货。小明成功省了1997元。 “道高一尺,…...

【I/O流之旅】File类-零基础入门指南
🎊专栏【Java】 🌺每日一句:看不清楚未来时,就比别人坚持久一点 ⭐欢迎并且感谢大家指出我的问题 目录 1.File概述 2.File构造方法 (1).根据文件路径创建文件对象 (2).根据父路径名字符串和子路径名字符串创建对象 (3).根据父路径对应文件对象和子路…...

ArrayList和LinkedList的区别有哪些?
ArrayList 和 LinkedList 是 Java 中常用的两种集合类,它们之间有一些重要的区别,主要涉及到其内部实现和性能特点: 内部实现: ArrayList 是基于动态数组实现的。它使用一个数组来存储元素,当数组已满并需要添加新元素…...

Pyhotn: Mac安装selenium没有chromedriver-114以上及chromedriver无法挪到/usr/bin目录下的问题
1.0 安装selenium 终端输入: pip install selenium 查看版本: pip show selenium2.0 安装chromedriver 查看chrome版本 网上大多数是,基本到114就停了。 https://registry.npmmirror.com/binary.html?pathchromedriver/ 各种搜索&#…...

Java TCP服务端多线程接收RFID网络读卡器上传数据
本示例使用设备介绍:WIFI/TCP/UDP/HTTP协议RFID液显网络读卡器可二次开发语音播报POE-淘宝网 (taobao.com) import java.io.IOException; import java.io.InputStream; import java.io.OutputStream; import java.net.ServerSocket; import java.net.Socket; impor…...
SpringCloud——服务网关——GateWay
1.GateWay是什么? gateway也叫服务网关,SpringCloud GateWay使用的是Webflux中的reactor-netty响应式编程组件,底层使用了Netty通讯框架。 gateway的功能有反向代理、鉴权、流量控制、熔断、日志监控...... 2.为什么不使用Zuul?…...

Linux程序的地址空间
Linux程序的地址空间 📟作者主页:慢热的陕西人 🌴专栏链接:Linux 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 本博客主要内容深刻理解了什么程序或者进程的地址…...

Docker安装Minio(稳定版)
1、安装 docker pull minio/minio:RELEASE.2021-06-17T00-10-46Z docker run -p 9000:9000 minio/minio:RELEASE.2021-06-17T00-10-46Z server /data 2、访问测试 3、MinIO自定义Access和Secret密钥 要覆盖MinIO的自动生成的密钥,您可以将Access和Secret密钥设为…...

大数据毕业设计选题推荐-超级英雄运营数据监控平台-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

视频转码教程:轻松制作GIF动态图,一键高效剪辑操作
随着社交媒体的兴起,GIF动态图已经成为了人们表达情感、分享精彩瞬间的重要方式。而将视频转化为GIF动态图,不仅可以方便地在社交媒体上分享,还可以延长视频的播放时长,吸引更多的观众。本篇文章将为大家介绍如何将视频轻松转化为…...
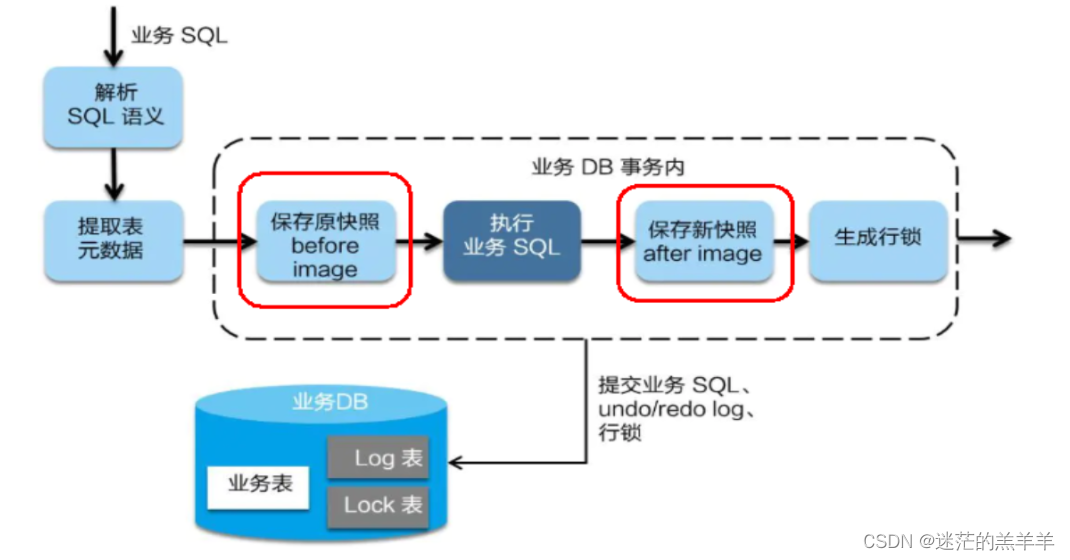
Seata分布式事务实现原理
Seata可以解决分布式事务问题,利用GlobalTransacational(name "fsp-create-order",rollbackFor Exception.class)注解就可以实现全局的事务管理,但是我们需要明白原理的实现。 我们举例创建订单——>调减库存——>调扣余额——>改订…...

Rasa NLU中的组件
Rasa NLU部分主要是解决NER(序列建模)和意图识别(分类建模)这2个任务。Rasa NLP是一个基于DAG的通用框架,图中的顶点即组件。组件特征包括有顺序关系、可相互替换、可互斥和可同时使用。有向无环图(DAG&…...
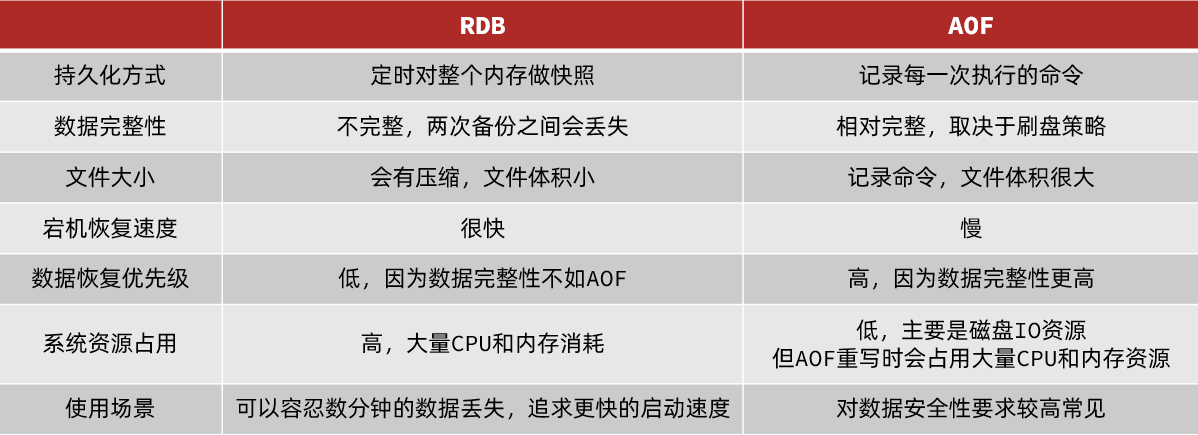
redis笔记 三 redis持久化
文章目录 Redis持久化RDB持久化执行时机RDB原理小结 AOF持久化AOF原理AOF配置AOF文件重写 RDB与AOF对比 Redis持久化 redis持久化是为了解决redis宕机时丢失数据的问题,Redis有两种持久化方案: RDB持久化AOF持久化 RDB持久化 RDB全称Redis Database …...

k8s-----数据存储
目录 一、数据存储的概念 二、基本存储 1、EmptyDir存储卷 2、hostPath存储卷 3、nfs共享存储卷 三、高级存储 1、PV(持久化卷) 2、PVC(持久化卷声明) 3、静态PV实验 4、动态PV实验 4.1 在stor01节点上安装nfs…...
macOS电池续航工具:Endurance中文
Endurance for Mac是一款强大而实用的电池管理和优化软件,专为MacBook设计。通过智能调整系统设置和管理后台应用,它能有效延长电池续航时间,提升工作和娱乐效率,成为你在各种场合下的得力助手。 Endurance for Mac软件的功能特色…...

栈(定义,基本操作,顺序存储,链式存储)
目录 1.栈的定义1.重要术语2.特点 2.栈的基本操作3.栈的顺序存储1.顺序栈的定义2.基本操作1.初始化2.进栈3.出栈4.读栈顶 3.共享栈 4.栈的链式存储 1.栈的定义 栈( Stack)是只允许在一端进行插入或删除操作的线性表。 一种受限的线性表,只能在栈顶进行插…...
在HTML单页面中,使用Bootstrap框架的多选框如何提交数据
1.引入Bootstrap CSS和JavaScript文件:确保在HTML页面的标签内引入Bootstrap的CSS和JavaScript文件。可以使用CDN链接或者下载本地文件。 <link rel"stylesheet" href"https://maxcdn.bootstrapcdn.com/bootstrap/4.5.2/css/bootstrap.min.css&q…...
当爱好变成职业,会不会就失去了兴趣?
当爱好变成职业,会不会就失去了兴趣? 当兴趣变成职业 1、学习能力变强了,积极主动性增加了。 2、学习努力变现了,赚到的更钱多了。 3、赚钱能力变强了,反过来再次促使兴趣发展(兴趣更大了....干劲更足了&…...
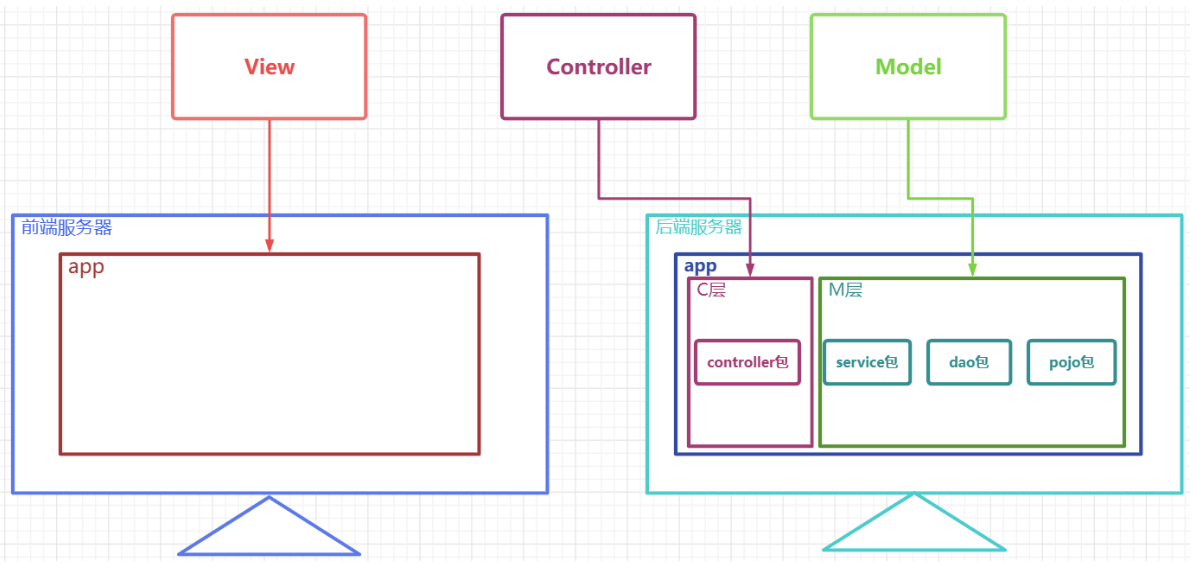
3-知识补充-MVC框架
3-知识补充-MVC框架 文章目录 3-知识补充-MVC框架MVC概述M、V、C各自负责功能及常用包MVC框架图非前后端分离框架图前后端分离框架图 MVC概述 MVC(Model、View、Controller)是软件工程中的一种**软件架构模式,它把软件系统分为模型、视图和控…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
