平衡树相关笔记
引入
二叉查找树
二叉查找树(Binary Search Tree),又名二叉搜索树。满足以下性质:
- 对于非空的左子树,左子树点权值小于根节点。
- 对于非空的右子树,左子树点权值大于根节点。
- 二叉查找树的左右子树均是二叉查找树。
平衡树
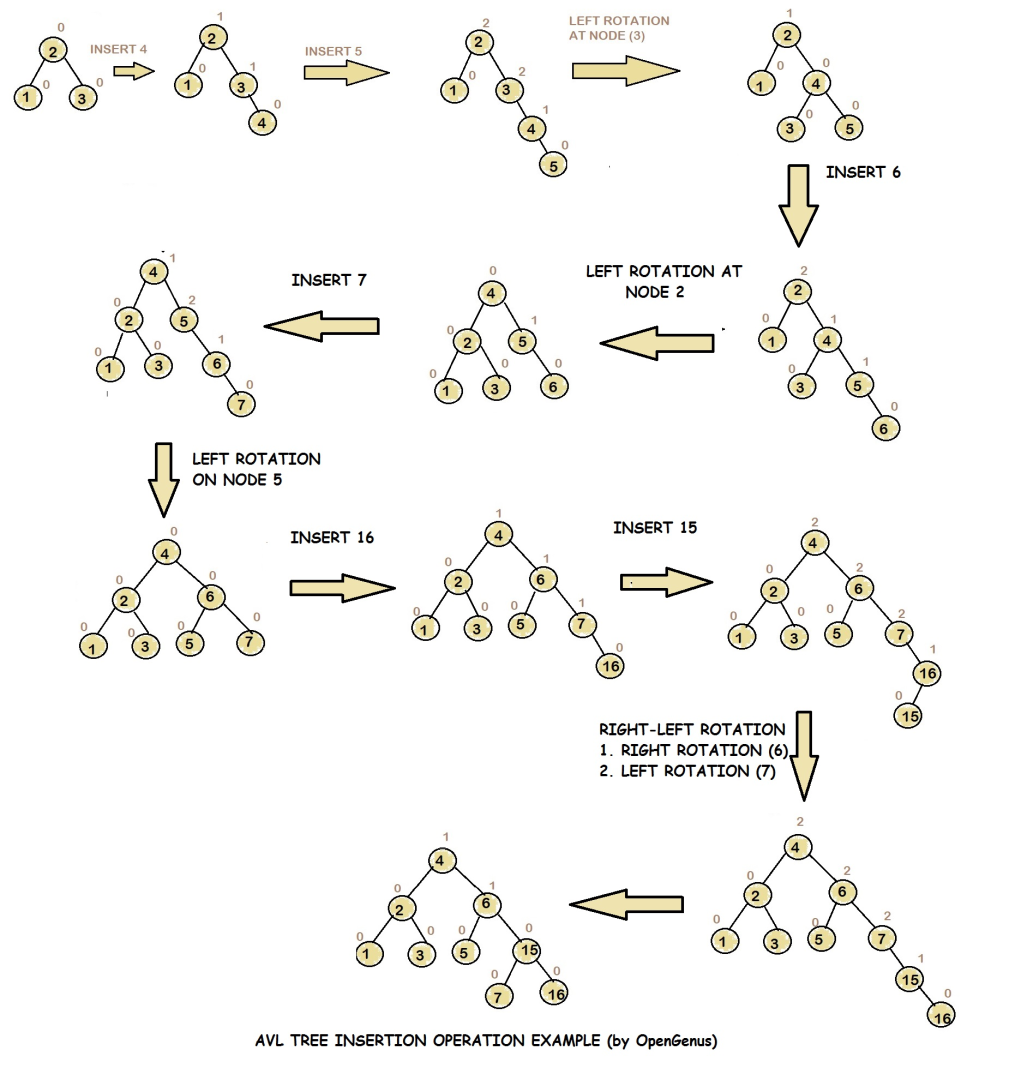
在维持二叉查找树性质的基础上,通过改变其形态,控制深度在 log n \log n logn 级别。
平衡树左右两个子树高度差不大于 1 1 1,否则需要进行左旋 / 右旋操作。
pb_ds
在 C++ 的 pb_ds 中有封装好的平衡树。
tree 类型的平衡树常数稍大,速度略慢。
声明方式
有以下声明(来源于官方文档):
template<typename Key,typename Mapped,typename Cmp_Fn = std::less<Key>,typename Tag = rb_tree_tag,template<typename Const_Node_Iterator,typename Node_Iterator,typename Cmp_Fn_,typename Allocator_>class Node_Update = null_tree_node_update,typename Allocator = std::allocator<char> >
class tree;
常用的定义方式为 tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update>。
- 第一个参数表示存储元素(Key)的类型;
- 第二个参数表示映射规则(Mapped-Policy)的类型,常用的是
null_type,表示无映射; - 第三个参数表示比较规则(
Cmp_Fn); - 第四个参数表示平衡树的类型(
Tag),有rb_tree_tag(红黑树)、splay_tree_tag等; - 第五个参数表示更新节点的策略(
Node_Update),默认为null_node_update,如果要使用查询排名相关操作,需要使用tree_order_statisitics_node_update。
常用操作
其中 x 表示存储元素的类型。
insert(x):插入元素 x x x。erase(x):删除元素 x x x。order_of_key(x):查询元素 x x x 的排名(前面有多少数比 x x x 小),返回值为整数。find_by_order(x):查询排名为 x x x 的元素对应的迭代器。lower_bound(x)、upper_bound(x):返回迭代器。join(x):将 x x x 树并入当前树,要求两树值域不能重叠。合并后 x x x 树被清空。split(x,b):小于等于 x x x 的属于当前树,其余的属于 b b b 树。size():返回大小。
以下是 P3369 【模板】普通平衡树 的代码。
注意用 pb_ds 实现的 tree 类似于一个 set,元素是不可重的。所以我们把元素以 pair 的形式存储,再记录一个元素被插入到 tree 的时间。
prev(it) 函数可以求迭代器 it 的前驱(即前一个位置)。注意求 x x x 的后继时,用 upper_bound() 操作的键值对应该是 pair<x,INT_MAX>,避免查找到和 x x x 相等但插入时间比 x x x 晚的元素。
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
using namespace std;tree<pair<int,int>,null_type,less<pair<int,int> >,rb_tree_tag,tree_order_statistics_node_update> t;int main()
{int n;cin>>n;for(int i=1;i<=n;i++){int op,x;cin>>op>>x;if(op==1) t.insert({x,i});if(op==2) t.erase(t.upper_bound({x,0}));if(op==3) cout<<t.order_of_key({x,0})+1<<endl;if(op==4){auto it=t.find_by_order(x-1);cout<<(*it).first<<endl;}if(op==5){auto it=prev(t.lower_bound({x,0}));cout<<(*it).first<<endl;}if(op==6){auto it=t.upper_bound({x,INT_MAX});cout<<(*it).first<<endl;}}return 0;
}
相关文章:

平衡树相关笔记
引入 二叉查找树 二叉查找树(Binary Search Tree),又名二叉搜索树。满足以下性质: 对于非空的左子树,左子树点权值小于根节点。对于非空的右子树,左子树点权值大于根节点。二叉查找树的左右子树均是二叉…...

ASP.net C# 用Aspose.pdf实现pdf合并
直接上代码,供参考,备忘! using System; using System.Collections.Generic; using System.Web; using System.Web.UI; using System.Web.UI.WebControls; using System.Data; using System.Data.SqlClient; using System.Xml; using System…...

C语言实现原码一位除
具体代码如下,直接运行即可。 #include <stdio.h> int main() {int i, a 0, b 0, c 0, flag 3; // flag相当于指针来指明Q的位置char x[6], y[6];int R[6], Q[6], yb[6], y1[6]; // yb是-y的补码,y1为绝对值yprintf("请输入X(带一位符号位四位数值位…...

three.js点滴yan(整理后)
场景、相机和渲染器 Three.js整个系统主要包含场景Scene、相机Camera和WebGL渲染器WebGLRenderer三大块,其中场景又包含模型和光源。WebGL渲染器的主要作用就是把相机对应场景渲染出来,显示在网页Cnavas画布上。 Three.js源码 Three.js各个构造函数对应…...

VMware安装CentOS最小化开发环境导引
目录 一、概要 二、介绍 三、下载 四、安装 4.1 创建虚拟机 4.2 安装CentOS 五、配置网卡 六、配置本地安装源 七、安装软件 7.1 gcc/g 7.2 C的atomic库 7.3 java 7.4 Cmake 7.5 MariaDB客户端(兼容mysql) 八、用户配置文件.bash_profile…...

服务器端编程/数据库驱动程序/RESTful API:介绍
目录 服务器端编程数据库驱动程序RESTful API 👍 点赞,你的认可是我创作的动力! ⭐️ 收藏,你的青睐是我努力的方向! ✏️ 评论,你的意见是我进步的财富! 服务器端编程 服务器端编程是一种计…...
Qwt QwtThermo绘制温度计
1.简介 QwtThermo 是一个基于 Qt 框架的类库,用于创建温度计控件。它提供了一些方便的功能来展示和处理温度计相关的数据。 QwtThermo 添加了特定于温度计的功能。 使用 QwtThermo,可以实现以下功能: 设置温度范围:可以通过设置…...

U_boot介绍
系统移植之前的了解的: 首先需要移植一个 bootloader 代码,这个 bootloader 代码用于启动 Linux 内核,bootloader 有很多,常用的就是 U-Boot;移植好 U-Boot 以后再移植 Linux 内核,移植完 Linux 内核以后 Linux 还不能…...
)
Flink -- window(窗口)
1、窗口主要分成三大种: 1、Time Window (时间窗口):固定时间触发一次窗口 a、SlidingEventTimeWindows: 滑动的事件时间窗口 public class Demo1TImeWindow {public static void main(String[] args) throws Exception {/*** 时…...

原语:串并转换器
串并转换器OSERDESE2 可被Select IO IP核调用。 OSERDESE2允许DDR功能 参考: FPGA原语学习与整理第二弹,OSERDESE2串并转换器 - 知乎 (zhihu.com) 正点原子。 ISERDESE2原语和OSERDESE2原语是串并转换器,他的的功能都是实现串行数据和并行…...
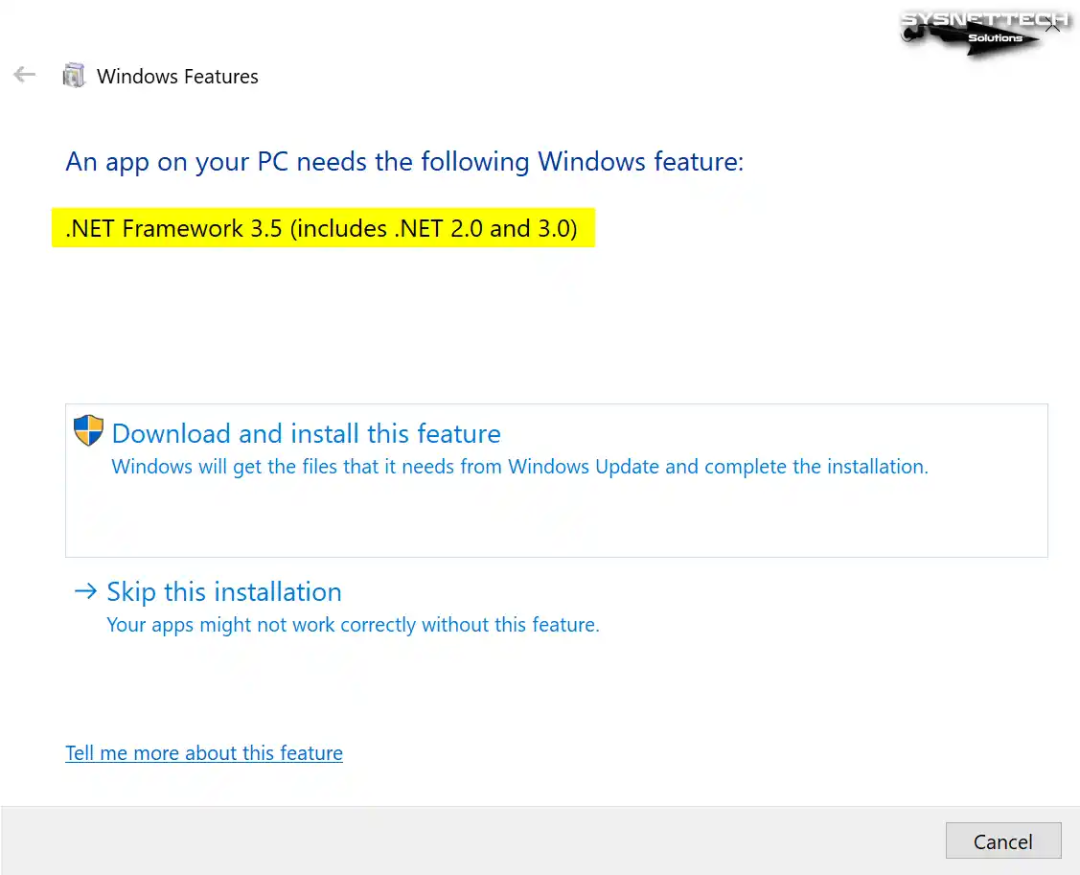
没网络也能安装.Net 3.5!如何脱机安装.NET Framework 3.5
.NET框架是由微软制定的一个软件框架。它有助于在Windows上运行控制台、Web或移动应用程序。此有用的工具适用于Windows设备。 如何脱机安装.NET Framework 3.5 如果你拥有Windows 10、8、8.1或7,有时第三方软件可能会导致问题。你可能会在图片中看到这样的问题。 看这张照片…...
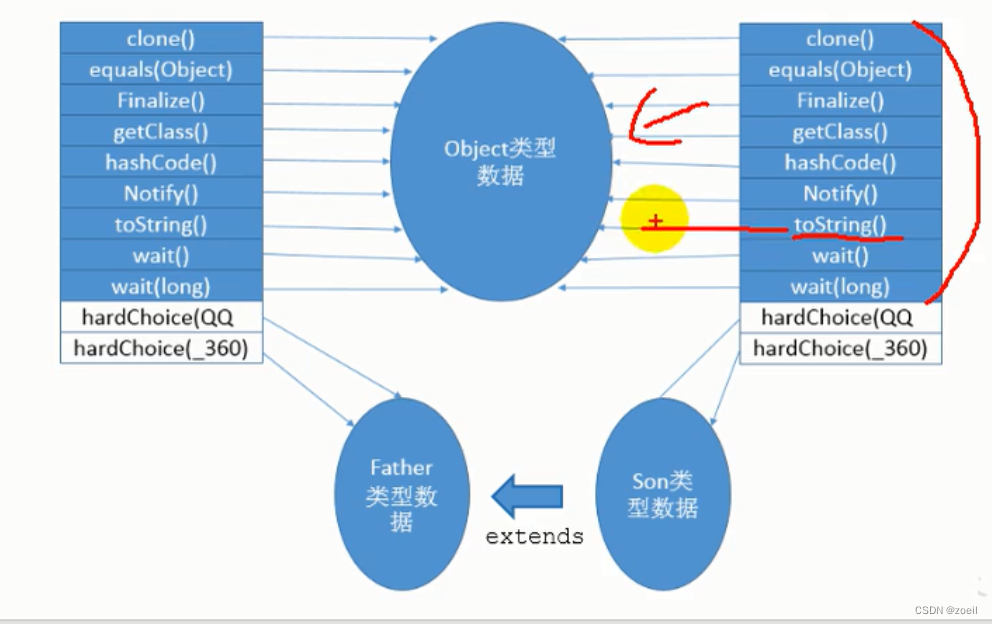
JVM运行时数据区-虚拟机栈
目录 一、内存中的栈 二、基本内容 三、优点 四、栈的存储单位 五、栈运行原理 六、栈的内部结构 (一)局部变量表 (二)操作数栈 (三)动态链接 (四)方法返回地址 …...

Java中介者模式
目录 定义 结构 案例 优点 缺点 使用场景 定义 又叫调停模式,定义一个中介角色来封装一系列对象之间的交互,使原有对象之间的耦合松散,且可以独立地改变它们之间的交互。 结构 中介者模式包含以下主要角色: 抽象中介者角…...
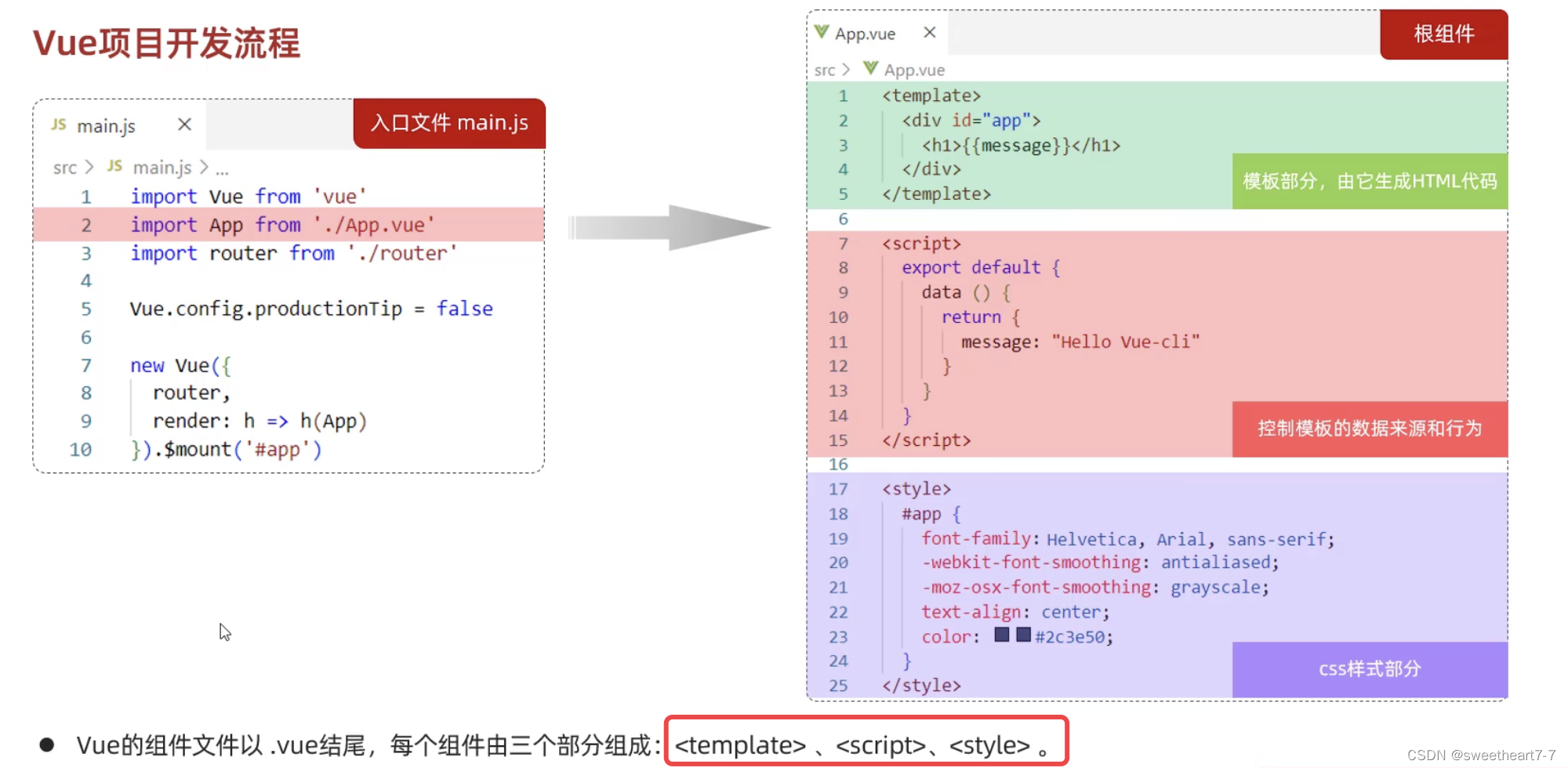
前端框架Vue学习 ——(五)前端工程化Vue-cli脚手架
文章目录 Vue-cliVue项目-创建Vue项目-目录结构Vue项目-启动Vue项目-配置端口Vue项目开发流程 Vue-cli 介绍:Vue-cli 是 Vue 官方提供的一个脚手架,用于快速生成一个 Vue 的项目模版 安装 NodeJS安装 Vue-cli npm install -g vue/cliVue项目-创建 图…...
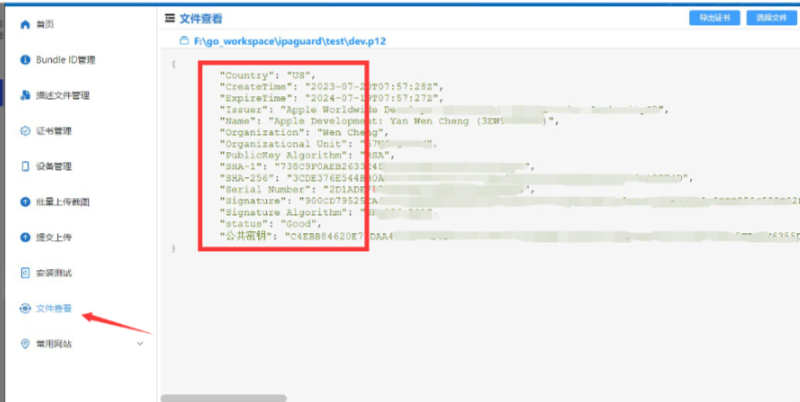
App备案-iOS云管理式证书 Distribution Managed 公钥及证书SHA-1指纹的获取方法
根据近日工业和信息化部发布的《工业和信息化部关于开展移动互联网应用程序备案工作的通知》,相信不少要进行IOS平台App备案的朋友遇到了一个问题,就是apple不提供云管理式证书的下载,也就无法获取公钥及证书SHA-1指纹。 已经上架的应用不想重…...

Spring -Spring之依赖注入源码解析
依赖注入底层原理流程图:Spring中Bean的依赖注入原理| ProcessOn免费在线作图,在线流程图,在线思维导图 Spring中到底有几种依赖注入的方式? 首先分两种: 手动注入自动注入 手动注入 在XML中定义Bean时,就是手动注入…...

Spire.Office for .NET 8.10.2 同步更新-Crk
Spire.Office for .NET是 E-iceblue 提供的企业级 Office .NET API 的组合。它包括Spire.Doc、Spire.XLS、Spire.Spreadsheet、Spire.Presentation、Spire.PDF、Spire.DataExport、Spire.OfficeViewer、Spire.PDFViewer、Spire.DocViewer、Spire.Barcode和Spire.Email。Spire.O…...
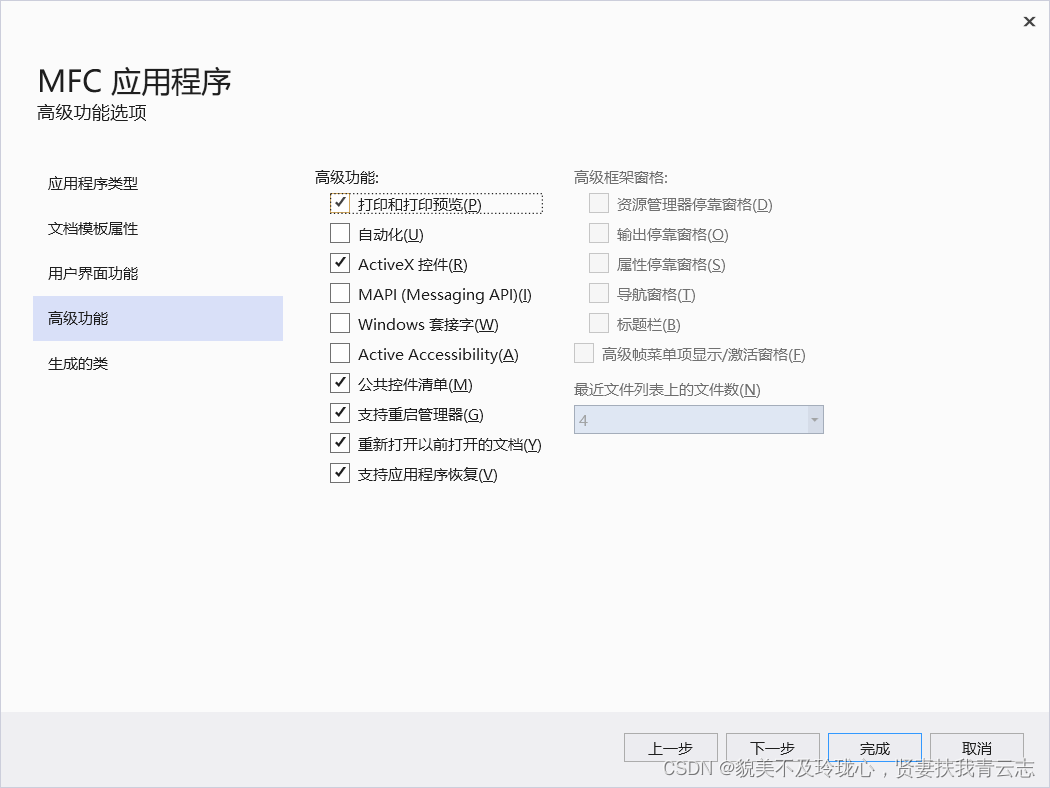
MFC 基础篇(一)
目录 一.SDK编程 二.为什么要学MFC? 三.MFC能做什么? 四.MFC开发环境搭建 五.MFC项目创建 六.消息映射机制 一.SDK编程 Application Programming Interface 应用程序编程接口。 Software Development Kit 软件开发工具包,一般会包括A…...

Android技术-修改SO导出符号
背景 经常在使用第三方SDK的时候会莫名其妙报错,其中最常见的一种就是SO符号冲突,比如libA.so静态链接了libC.a,而libB.so动态链接了libC.so。这样便会导致符号冲突。又或者在使用不同版本的动态库,也会造成符号冲突。 报错案例 案例1 DEB…...

flutter 打包apk
Flutter项目打包生成APK_flutter打包apk_文阿花的博客-CSDN博客 关于iconData可能出现的错误: flutter build apk 打包报错调试过程 - 掘金 (juejin.cn) 使用命令行:flutter build apk --no-tree-shake-icons...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
