当前位置：首页 > news >正文

图片做多的网站是哪个/网站交换链接的常见形式

news 文章来源：https://blog.csdn.net/passxgx/article/details/134192093 2025/2/22 5:17:43

图片做多的网站是哪个,网站交换链接的常见形式,做直播网站需要学什么软件,wordpress更改到子目录一、消元矩阵消元矩阵执行消元步骤用到的矩阵。从第 i i i 个方程减去 l i j l_{ij} lij 乘第 j j j 个方程（将 x j x_j xj 从第 i i i 行中消去）。我们需要很多个简单的矩阵 E i j E_{ij} Eij，每一个对应一个主对角线下方要消…

一、消元矩阵

消元矩阵执行消元步骤用到的矩阵。从第 $i$ 个方程减去 $l_{ij}$ 乘第 $j$ 个方程（将 $x_j$ 从第 $i$ 行中消去）。我们需要很多个简单的矩阵 $E_{ij}$ ，每一个对应一个主对角线下方要消除的非零数字。
后面我们会把所有的 $E_{ij}$ 结合成一个矩阵 $E$ ，一次性完成消元。最简洁的方法是将所有的逆矩阵 $E_{ij})^{-1}$ 结合成一个整体的矩阵 $L=E^{-1}$ 。本节的内容：

了解每一个步骤都是一次矩阵乘法。
将所有步骤的 $E_{ij}$ 结合成一个消元矩阵 $E$ 。
了解每一个 $E_{ij}$ 如何变成逆矩阵 $E_{ij})^{-1}$ 。
组合所有的逆矩阵 $E_{ij})^{-1}$ （右序）变成 $L$ 。

$L$ 的特殊性质是其所有的乘数 $l_{ij}$ 都是有序的，这些乘数在 $E$ 中是混乱的（从 $A$ 到 $U$ 的前向消元），在 $L$ 中（撤销消元，从 $U$ 返回到 $A$ ）会变得有序。反向可以让这些步骤与矩阵 $E_{ij})^{-1}$ 落在反向序列中，防止混乱。

二、矩阵乘向量 Ax = b

上节的例题 $3\times3$ 的方程组可以简写乘矩阵的形式 $A\boldsymbol x=\boldsymbol b$ ： $\begin{matrix}2x_1+4x_2-2x_3=2\\4x_1+9x_2-3x_3=8\\-2x_1-3x_2+7x_3=10\end{matrix}\kern 6pt等价于\kern 6pt\begin{bmatrix}\kern 7pt2&\kern 7pt4&-2\\\kern 7pt4&\kern 7pt9&-3\\-2&-3&\kern 7pt7\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}2\\8\\10\end{bmatrix}\kern 10pt(2.3.1)$ 左侧的 $9$ 个数字组成矩阵 $A$ ，矩阵 $A$ 乘 $\boldsymbol x$ 得到三个方程。
$A$ 乘 $\boldsymbol x$ 复习：矩阵乘向量得到向量。当方程的数目和未知数的数目相等时，矩阵为方阵。方阵通常表示为 $n\times n$ 。向量 $\boldsymbol x$ 在 $n$ 维空间。 $未知数是\kern 5pt\boldsymbol x=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}\kern 10pt解是\kern 5pt\boldsymbol x=\begin{bmatrix}-1\\\kern 7pt2\\\kern 7pt2\end{bmatrix}$ 重点： $A\boldsymbol x=\boldsymbol b$ 表示方程的行形式，也表示列形式： $列形式\kern 10ptA\boldsymbol x=(-1)\begin{bmatrix}\kern 7pt2\\\kern 7pt4\\-2\end{bmatrix}+2\begin{bmatrix}\kern 7pt4\\\kern 7pt9\\-3\end{bmatrix}+2\begin{bmatrix}-2\\-3\\\kern 7pt7\end{bmatrix}=\begin{bmatrix}2\\8\\10\end{bmatrix}=\boldsymbol b\kern 10pt(2.3.2)$ $A\boldsymbol x$ 是 $A$ 列的线性组合，要计算 $A\boldsymbol x$ 的分量时，可以使用矩阵乘法的行形式， $A\boldsymbol x$ 的分量就是 $\boldsymbol x$ 与 $A$ 每行的点积。可以使用累加表示： $A\boldsymbol x\,的第一分量：(-1)(2)+(2)(4)+(2)(-2)\kern 48pt\\A\boldsymbol x\,第 \,i\,分量：(\textrm{row}\,\,i)\cdot\boldsymbol x=a_{i1}x_1+a_{i2}x_2+\cdots+a_{in}x_n$ 符号记为： $\sum_{j=1}^{n}a_{ij}x_j$
$\sum$ 表示累加，从 $j = 1$ 开始到 $j = n$ 结束，从 $a_{i1}x_1$ 开始一直累加到 $a_{in}x_n$ ，得到点积 $(\textrm{row}\,\,i)\cdot\boldsymbol x$ 。
矩阵表示法：第 1 行第 1 列的元素（左上角）是 $a_{11}$ ，第 1 行第 3 列的元素是 $a_{13}$ ，第 3 行第 1 列的元素是 $a_{31}$ （行数在前，列数在后）。一般规则： $a_{ij}=A(i,j)$ ，位置在第 $i$ 行 $j$ 列。

【例1】矩阵有 $a_{ij}=2i+j$ ，则 $a_{11}=3,a_{12}=4,a_{21}=5$ 。下面是由行得到 $A\boldsymbol x$ ，分别用数字和字母表示： $\begin{bmatrix}3&4\\5&6\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix}=\begin{bmatrix}3\cdot2+4\cdot1\\5\cdot2+6\cdot1\end{bmatrix}\kern 15pt\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}a_{11}x_1+a_{12}x_2\\a_{21}x_1+a_{22}x_2\end{bmatrix}$

三、一个消元步骤的矩阵形式

方程 $A\boldsymbol x=\boldsymbol b$ ，从第二个式子中减去 $2$ 乘第一个式子，在右侧， $\boldsymbol b$ 的第二个分量减去 $2$ 乘第一个分量： $第一步\kern 10pt\boldsymbol b=\begin{bmatrix}2\\8\\10\end{bmatrix}\kern 10pt变为\kern 10pt\boldsymbol b_{\textrm {new}}=\begin{bmatrix}2\\4\\10\end{bmatrix}$ 若使用矩阵形式实现上述步骤，则需要一个消元矩阵 $E$ 乘 $\boldsymbol b$ 得到 $\boldsymbol b_{\textrm{new}}=E\boldsymbol b$ ，从 $b_2$ 减去 $2b_1$ ： $消元矩阵\kern 10ptE=\begin{bmatrix}\kern 7pt1&0&0\\-2&1&0\\\kern 7pt0&0&1\end{bmatrix}$ 用 $E$ 乘的结果是使得第 $2$ 行减去 $2$ 乘第 $1$ 行，而第 $1 、 3$ 行保持不变： $\begin{bmatrix}\kern 7pt1&0&0\\-2&1&0\\\kern 7pt0&0&1\end{bmatrix}\begin{bmatrix}2\\8\\10\end{bmatrix}=\begin{bmatrix}2\\4\\10\end{bmatrix}\kern 10pt\begin{bmatrix}\kern 7pt1&0&0\\-2&1&0\\\kern 7pt0&0&1\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}=\begin{bmatrix}b_1\\b_2-2b_1\\b_3\end{bmatrix}$ $E$ 的第 $1 、 3$ 行是来自于单位矩阵 $I$ ，它们不会改变第一和第三分量，新的第二个分量 $4$ 是消元之后出现的，即 $b_2-2b_1$ 。
消元矩阵 $E$ 是将单位矩阵 $I$ 其中的一个 $0$ 变为乘数 $- l$ 。

单位矩阵对角线上的元素都是 $1$ ，其余的元素全为 $0$ 。对于任意的 $\boldsymbol b$ 都有 $I\boldsymbol b=\boldsymbol b$ 。消元矩阵 $E_{ij}$ 在 $i, j$ 位置处多了一个非零元素 $- l$ ，被 $E_{ij}$ 乘会使得第 $i$ 行减去 $l$ 乘第 $j$ 行。

【例2】矩阵 $E_{31}$ 的位置 $3, 1$ 是 $- l$ ： $单位矩阵\kern 10ptI=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\kern 10pt消元矩阵\kern 5ptE_{31}=\begin{bmatrix}\kern 7pt1&0&0\\\kern 7pt0&1&0\\-l&0&1\end{bmatrix}$ $I$ 乘 $\boldsymbol b$ 仍然得到 $\boldsymbol b$ ，但是 $E_{31}$ 乘 $\boldsymbol b$ 会从 $\boldsymbol b$ 的第三分量减去 $l$ 乘第一分量。当 $l = 4$ 时，第三分量为 $9 - 4 = 5$ ： $I\boldsymbol b=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}1\\3\\9\end{bmatrix}=\begin{bmatrix}1\\3\\9\end{bmatrix}\kern 10ptE_{31}\boldsymbol b=\begin{bmatrix}1&0&0\\0&1&0\\-4&0&1\end{bmatrix}\begin{bmatrix}1\\3\\9\end{bmatrix}=\begin{bmatrix}1\\3\\5\end{bmatrix}$ $A\boldsymbol x=\boldsymbol b$ 进行消元时，两侧都会被 $E_{31}$ 乘， $E_{31}$ 的目的是在矩阵 $(3, 1)$ 位置处产生 $0$ 。
进行消元时，从矩阵 $A$ 开始，需要使用多个 $E$ 使得主元下方位置都产生 $0$ ，第一个 $E$ 是 $E_{21}$ ，最终得到三角形 $U$ 。
消元过程中，向量 $\boldsymbol x$ 不会变化，解 $\boldsymbol x$ 也不会因消元而改变。只有系数矩阵会改变。若 $A\boldsymbol x=\boldsymbol b$ ，则 $EA\boldsymbol x=E\boldsymbol b$ ，新矩阵 $E A$ 是 $E$ 乘 $A$ 的结果。

四、矩阵乘法

两个矩阵如何相乘？若第一个矩阵是 $E$ ，目标是 $E A$ ， $E$ 会使得 $A$ 的行 $2$ 减去 $2$ 乘行 $1$ ，乘数是 $2$ ： $EA=\begin{bmatrix}\kern 7pt1&0&0\\-2&1&0\\\kern 7pt0&0&1\end{bmatrix}\begin{bmatrix}\kern 7pt2&\kern 7pt4&-2\\\kern 7pt4&\kern 7pt9&-3\\-2&-3&\kern 7pt7\end{bmatrix}=\begin{bmatrix}\kern 7pt2&\kern 7pt4&-2\\\kern 7pt\textbf0&\kern 7pt\textbf1&\kern 7pt\textbf1\\-2&-3&\kern 7pt7\end{bmatrix}\kern 5pt(得到一个零)\kern 10pt(2.3.3)$ 这个步骤没有改变 $A$ 的行 $1$ 和行 $3$ ，它们在 $E A$ 中保持不变，只改变了行 $2$ ，行 $2$ 减去了行 $1$ 的 $2$ 倍。矩阵乘法与消元法达成了相同的目的，新的系统为 $EA\boldsymbol x=E\boldsymbol b$ 。
$EA\boldsymbol x$ 虽然简单，确含有一个巧妙的思想。从 $A\boldsymbol x=\boldsymbol b$ 开始，两边同时用 $E$ 乘得到 $E(A\boldsymbol x)=E\boldsymbol b$ 。使用矩阵乘法，也是 $(EA)\boldsymbol x=E\boldsymbol b$ 。

第一个是 $E$ 乘 $A\boldsymbol x$ ，第二个是 $E A$ 乘 $\boldsymbol x$ ，它们是相同的。

括号不需要了，可直接写成 $EA\boldsymbol x$ 。
这个规律可以扩展至有多个列向量的矩阵 $C$ ，计算 $E A C$ 可以先算 $A C$ ，也可以先算 $E A$ ，这个规律就是结合律。
注意通常情况下 $E A$ 不等于 $A E$ 。当 $E$ 乘在右侧时，它作用于 $A$ 的列而不是行。 $A E$ 会使得 $A$ 的列 $1$ 减去 $2$ 乘列 $2$ $结合律正确\kern 10ptA(BC)=(AB)C\\交换律错误\kern 10pt通常AB\neq BA\kern 12pt$ 矩阵乘法还有另外一个要求，假设 $B$ 只有一列（列 $\boldsymbol b$ ），矩阵 - 矩阵相乘 $EB$ 应和矩阵 - 向量相乘的法则一致。甚至矩阵乘法 $EB$ 可以一次乘一列：
如果 $B$ 有多个列 $b_1,b_2,b_3$ ，则 $EB$ 的列为 $Eb_1,Eb_2,Eb_3$ 。 $矩阵乘法\kern 10ptEB=E[b_1,b_2,b_3]=[Eb_1,Eb_2,Eb_3]\kern 15pt(2.3.4)$ 对于式（2.3.3），也可以使用这项性质。 $E$ 乘 $A$ 的列 $3$ ，也可以得到正确的 $E A$ 的列 $3$ ： $\begin{bmatrix}\kern 7pt1&0&0\\-2&1&0\\\kern 7pt0&0&1\end{bmatrix}\begin{bmatrix}-2\\-3\\\kern 7pt7\end{bmatrix}=\begin{bmatrix}-2\\\kern 7pt1\\\kern 7pt7\end{bmatrix}\kern 10ptE(A的列\kern 1ptj)=EA\,的列\,j$ 矩阵乘法有三种处理方式（行、列、整个矩阵）都可以得到正确的结果。

五、行交换矩阵 $P_{ij}$

从行 $i$ 减去行 $j$ 使用 $E_{ij}$ ，交换或置换这些行使用另外一种矩阵 $P_{ij}$ （置换矩阵）。如果主元位置出现零时，那么就需要行交换，往下方看，主元这一列可能存在非零数字，交换这两行就有主元了，消元也可以继续进行。
置换矩阵 $P_{23}$ 可以交换行 $2$ 与行 $3$ ，将单位矩阵的行 $2$ 与行 $3$ 交换，就可得到 $P_{23}：$ $置换矩阵\kern 10ptP_{23}=\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}$ 这个就是行交换矩阵。 $P_{23}$ 乘任意的列向量，都会使其第二分量和第三分量交换，因此也可以交换矩阵的行 $2$ 与行 $3$ ： $\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}\begin{bmatrix}1\\3\\5\end{bmatrix}=\begin{bmatrix}1\\5\\3\end{bmatrix},\kern 13pt\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}\begin{bmatrix}2&4&1\\0&0&3\\0&6&5\end{bmatrix}=\begin{bmatrix}2&4&1\\0&6&5\\0&0&3\end{bmatrix}$ $P_{23}$ 交换了行 $2$ 与行 $3$ ，使得主元的位置从 $0$ 变成了 $6$ 。
置换矩阵可以交换行的顺序。例如行 $1, 2, 3$ 可以变为行 $3, 1, 2$ 。

行交换矩阵： 单位矩阵的行 $i$ 与 $j$ 交换顺序可以得到 $P_{ij}$ 。当置换矩阵 $P_{ij}$ 乘一个矩阵时，则该矩阵交换行 $i$ 与行 $j$ 。

$交换方程\,1\,与方程\,3，左边乘上 P_{13}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$ 一般来说要将主元移至对角线时，需要用到置换矩阵。

六、增广矩阵

下面是一个矩形矩阵也是来源于原始方程，但是包括了右侧的 $\boldsymbol b$ 。
关键点：消元法对于 $A$ 与 $\boldsymbol b$ 有相同的行操作，我们可以将 $\boldsymbol b$ 当做一个额外的列，一起进行消元。额外列 $\boldsymbol b$ 加入后，矩阵 $A$ 就变大了，称为增广（augmented）矩阵： $\pmb{增广矩阵}\kern 5pt[A\kern 6pt\boldsymbol b]=\begin{bmatrix}\kern 7pt2&\kern 7pt4&-2&\pmb2\\\kern 7pt4&\kern 7pt9&-3&\pmb8\\-2&-3&\kern 7pt7&\pmb{10}\end{bmatrix}$ 消元法作用于矩阵的整个行， $E$ 同时乘上左侧和右侧，得到方程 $2$ 减去 $2$ 乘方程 $1$ ，这个步骤同时发生在 $[E\kern 6pt\boldsymbol b]$ ： $\begin{bmatrix}\kern 7pt1&0&0\\-2&1&0\\\kern 7pt0&0&1\end{bmatrix}\begin{bmatrix}\kern 7pt2&\kern 7pt4&-2&2\\\kern 7pt4&\kern 7pt9&-3&8\\-2&-3&\kern 7pt7&10\end{bmatrix}=\begin{bmatrix}\kern 7pt2&\kern 7pt4&-2&2\\\kern 7pt0&\kern 7pt1&\kern 7pt1&4\\-2&-3&\kern 7pt7&10\end{bmatrix}$ 新的第二行包含 $0, 1, 1, 4$ ，新的方程 $2$ 为 $x_2+x_3=4$ 。矩阵乘法同时作用于行和列： $\pmb{行：}E\,的每一行作用在[A\kern 6pt\boldsymbol b]得到 [EA\kern 6ptE\boldsymbol b]的一行\\\pmb{列：}E作用于 [A\kern 6pt\boldsymbol b]的每一列得到[EA\kern 6ptE\boldsymbol b]的一列$ 注意作用（act）的意义。矩阵 $A$ 作用于 $\boldsymbol x$ 得到 $\boldsymbol b$ 。矩阵 $E$ 作用于 $A$ 得到 $E A$ 。消元法的过程就是一系列的行运算，也是矩阵乘法。从 $A$ 到 $E_{21}A$ ，再到 $E_{31}E_{21}A$ ，最后是 $E_{32}E_{31}E_{21}A$ ，它是个三角矩阵。
方程右侧的引入形成了增广矩阵，最后结果是一个方程的三角形系统。

七、主要内容总结

$A\boldsymbol x=(x_1乘列\,1)+\cdots+(x_n乘列\,n)$ ， $(A\boldsymbol x)_i=\sum_{j=1}^{n}a_{ij}x_j$ 。
$单位矩阵 = I$ ， $消元矩阵=E_{ij},使用乘数\,l_{21}$ ， $置换矩阵=P_{ij}$ 。
$E_{21}$ 乘 $A\boldsymbol x=\boldsymbol b$ ，得到方程 $2$ 减去 $l_{21}$ 乘方程 $1$ 。 $l_{21}$ 是消元矩阵 $E_{21}$ 在位置 $(2, 1)$ 处的元素。
增广矩阵 $\begin{bmatrix}A&\boldsymbol b\end{bmatrix}$ ，消元步骤得到 $\begin{bmatrix}E_{21}A&E_{21}\boldsymbol b\end{bmatrix}$ 。
$A$ 乘任意矩阵 $B$ ，等于 $A$ 分别乘 $B$ 的每一列。

八、例题

【例3】什么样的 $3\times3$ 矩阵 $E_{21}$ 使得矩阵 $A$ 的行 $2$ 减去 $4$ 乘行 $1$ ？什么样的矩阵 $P_{32}$ 交换矩阵 $A$ 的行 $2$ 与行 $3$ ？如果对矩阵 $A$ 右乘而不是左乘，描述 $AE_{21}$ 与 $AP_{32}$ 的结果？
解：对单位矩阵 $I$ 执行一些运算，可得 $E_{21}=\begin{bmatrix}\kern 7pt1&0&0\\-4&1&0\\\kern 7pt0&0&1\end{bmatrix},\kern 15ptP_{32}=\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}$ $E_{21}$ 乘在矩阵 $A$ 的右侧使得 $A$ 的列 $1$ 减去 $4$ 乘列 $2$ ， $P_{32}$ 乘在右侧会交换列 $2$ 与列 $3$ 。

【例4】写出下面方程组的增广矩阵 $\begin{bmatrix}A&\boldsymbol b\end{bmatrix}$ ： $\kern 4ptx+2y+2z=1\\4x+8y+9z=3\\\kern 24pt3y+2z=1$ 使用 $E_{21}$ 和 $P_{32}$ 得到三角形系统。用回代求解方程组。组合矩阵 $P_{32}E_{21}$ 一次做了那些工作？
解： $E_{21}$ 使列 $1$ 的 $4$ 变为 $0$ ，但是 $0$ 也出现在了列 $2$ ： $\begin{bmatrix}A&\boldsymbol b\end{bmatrix}=\begin{bmatrix}1&2&2&1\\\pmb4&8&9&3\\0&3&2&1\end{bmatrix},\kern 10ptE_{21}\begin{bmatrix}A&\boldsymbol b\end{bmatrix}=\begin{bmatrix}1&2&2&\kern 7pt1\\\pmb0&\pmb0&1&-1\\0&3&2&\kern 7pt1\end{bmatrix}$ $P_{32}$ 交换行 $2$ 与行 $3$ ，回代可以求出解 $z, y, x$ ： $P_{32}E_{21}\begin{bmatrix}A&\boldsymbol b\end{bmatrix}=\begin{bmatrix}1&2&2&\kern 7pt1\\0&3&2&\kern 7pt1\\0&0&1&-1\end{bmatrix},\kern 10pt\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}\kern 7pt1\\\kern 7pt1\\-1\end{bmatrix}$ 组合矩阵 $P_{32}E_{21}$ 可以同时完成两个步骤， $P_{32}$ 作用于 $E_{21}$ ： $\begin{matrix}\pmb{一个矩阵}\\\pmb{两个步骤}\end{matrix}\kern 10ptP_{32}E_{21}=E_{21}交换行\,2与行\,3=\begin{bmatrix}\kern 7pt1&0&0\\\kern 7pt0&0&1\\-4&1&0\end{bmatrix}$ 【例5】矩阵乘法有两种方式。第一， $A$ 的行乘 $B$ 的列；第二， $A$ 的列乘 $B$ 的行，这个不寻常的方法会产生两个矩阵，相加后得到 $A B$ 。两种方法各需要多少次乘法？ $\pmb{两种方法}\kern 10ptAB=\begin{bmatrix}3&4\\1&5\\2&0\end{bmatrix}\begin{bmatrix}2&4\\1&1\end{bmatrix}=\begin{bmatrix}10&16\\7&9\\4&8\end{bmatrix}$ 解： $A$ 的行乘 $B$ 的列是向量的点积： $(\textrm{row}\,1)\cdot(\textrm{column}\,1)=\begin{bmatrix}3&4\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix}=10\kern 7pt是\,AB\,在(1,1)处的元素\\(\textrm{row\,2})\cdot(\textrm{column}\,1)=\begin{bmatrix}1&5\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix}=7\kern 13pt是\,AB\,在(2,1)处的元素$ 总共要做 $6$ 个点积，每个有 $2$ 次乘法，总共需要 $(3\cdot2\cdot2)=12$ 次乘法。 $A B$ 也可以是 $A$ 的列乘 $B$ 的行，一列乘一行是一个矩阵，也是 $12$ 次乘法： $AB=\begin{bmatrix}3\\1\\2\end{bmatrix}\begin{bmatrix}2&4\end{bmatrix}+\begin{bmatrix}4\\5\\0\end{bmatrix}\begin{bmatrix}1&1\end{bmatrix}=\begin{bmatrix}6&12\\2&4\\4&8\end{bmatrix}+\begin{bmatrix}4&4\\5&5\\0&0\end{bmatrix}$

图片做多的网站是哪个/网站交换链接的常见形式

一、消元矩阵

二、矩阵乘向量 Ax = b

三、一个消元步骤的矩阵形式

四、矩阵乘法

五、行交换矩阵 $P_{ij}$

六、增广矩阵

七、主要内容总结

八、例题

相关文章：

2.3 矩阵消元

Docker 从构建开始导出一个镜像

案例研究｜腾讯音乐娱乐集团与JumpServer共探安全运维审计解决方案

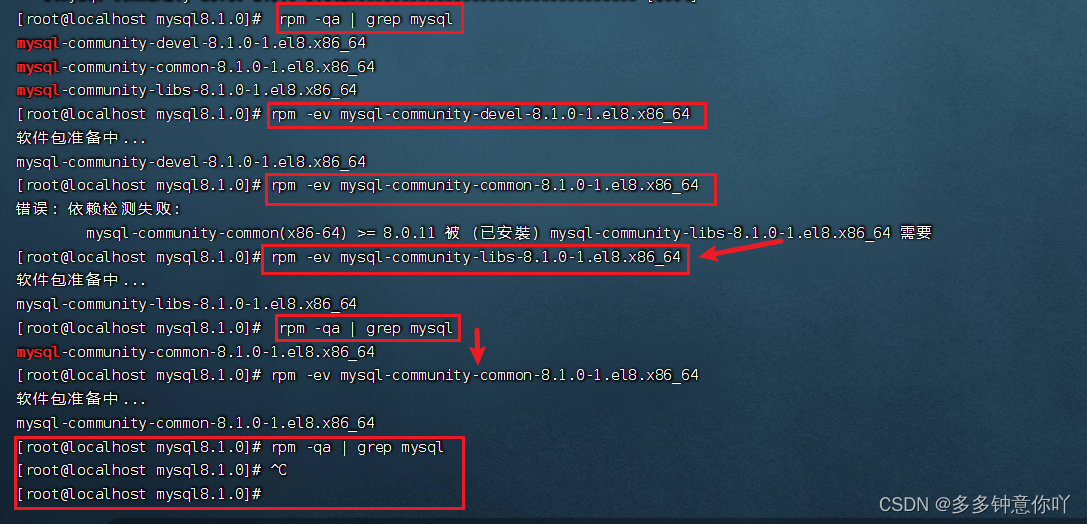
如何卸载在linux下通过rpm安装的mysql

docker复制镜像文件

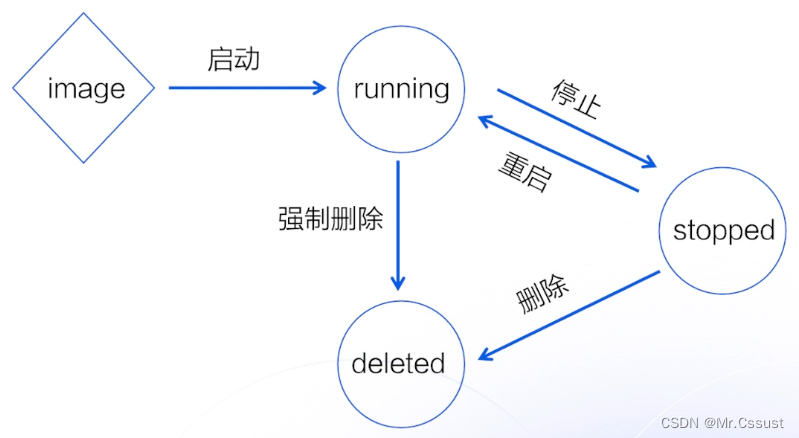
自动驾驶学习笔记（六）——Apollo安装

四阶龙格库塔与元胞自动机

Mac安装opencvJava踩坑

YOLOv8-Pose推理详解及部署实现

django+drf+vue 简单系统搭建（1） - django创建项目

各种NoSQL数据库

基于8086家具门安全控制系统设计

k8s：kubectl 详解

壹基金防灾减灾宣传进社区提升家庭安全能力

抖音自动发评论软件下载方法与其使用方法与案例分析分享

Java代码实现当前时间增加3个月

互联网系统安全（一）

C# TabControl实现为每一个TabPage添加关闭按钮

Win10系统下torch.cuda.is_available()返回为False的问题解决

零代码编程：用ChatGPT批量将Mp4视频转为Mp3音频

微服务项目,请求从发出到后端处理器的历程

pandas教程：String Manipulation 字符串处理和正则表达式re

Apache Doris 是什么

【NeurIPS 2020】基于蒙特卡罗树搜索的黑箱优化学习搜索空间划分

面试题：线上MySQL的自增id用尽怎么办？

Java集合框架：Collection 与 Map 接口深度解析

qt多线程例子，不断输出数字

基于厨师算法的无人机航迹规划-附代码

设计模式的六大原则

原文远知行COO张力加盟逐际动力自动驾驶进入视觉时代？

一、消元矩阵

二、矩阵乘向量 Ax = b

三、一个消元步骤的矩阵形式

四、矩阵乘法

五、行交换矩阵 P i j P_{ij} Pij​

六、增广矩阵

七、主要内容总结

八、例题

相关文章：

五、行交换矩阵 $P_{ij}$