电路布线问题动态规划详解(做题思路)
对于电路布线问题,想必学过动态规划的大家都很清除。今天就来讲解一下这个动态规划经典题目。
目录
- 问题描述
- 输入
- 分析
- 最优子结构
- 代码
问题描述
在一块电路板的上、下2端分别有n个接线柱。根据电路设计,要求用导 线(i,π(i))将上端接线柱与下端接线柱相连,如图所示。其中π(i)是 {1,2,…,n}的一个排列。导线(i,π(i))称为该电路板上的第i条连线。对于任 何1≤i<j≤n,第i条连线和第j条连线相交的充分且必要的条件是π(i)>π(j)。 电路布线问题要确定将哪些连线安排在第一层上,使得该层上有尽可能 多的连线。换句话说,该问题要求确定导线集Nets={(i,π(i)),1≤i≤n}的最 大不相交子集。
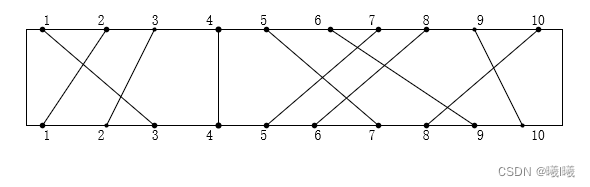
输入
两行输入
第一行是一排接线柱的个数
第二行是上接线柱对应的下接线柱位置,即下文的p(i)
对于上图输入就是
10
3 1 2 4 7 9 5 6 10 8
分析
那么什么是最大不相交子集呢。咱们来一个一个字 的 扣含义。
首先最大就是字面意思最大的,最多的。
其次不相交也是字面意思,就是单纯的两条线不能有交点。
最后子集的定义是如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集(通俗点说就是在给出的导线集合里面,挑选几条导线,这挑选的导线组成的集合就是子集)。
那么组合起来说的就是,在现有的线中挑选数量最多的导线且它们还不相交
我们发现这个题,好像不能从考虑最后一个步骤来推导了,我们好像还真不太好找出最后一个问题是什么。那么我们就换一种思路,回想以前的动态规划好像都是在数组中记录数值,供以后使用的而且都是一行一行的计算子问题。那我们先定义一个数组,考虑到有上下两排线,那就定义二维数组吧.。
设dp[i][j]表示前i个上接线柱和前j个下接线柱组成的问题的最优解包含的导线的数量(即前i个上接线柱和前j个下接线柱组成的集合的最大不相交子集中包含的导线数)
为了方便说明再来定义一些规则:
上接线柱集合(1,2,3,4…n)
下接线柱集合(p(1),p(2),p(3),p(4)…p(n))
p(n)代表上层接线柱n对应的下层接线柱的编号。例如下图中上接线柱1,p(1)就是3
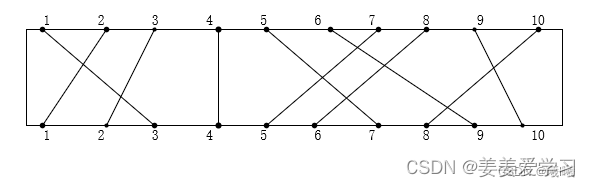
接下来以上图为例先从第一行来看,来找一下规律触发一下灵感
(第1步) i=1,j=1

(第2步) i=1,j=2

(第3步) i=1,j=3

唉突然发现此时,增加了一个,那就来想一想是什么原因让他增加的呢。我们发现当j>=p(1)时他就增加了,接下来继续看。
(第4步) i=1,j=3
然后类似的一直到 j==10 的时候
… …
(第10步) i=1,j=10

发现第一行除了j==3的时候增加了一个,其他的j>=p(1)的情况并没有增加为什么会这样呢?思考一下。因为我们的i是等于1的所以我们的dp[1][j]他最多只有一条线,我们上接线柱只包含了一个,所以他只能是小于等于一的数
这就给我们一个灵感我们可以根据i,p(i)的关系进行动态规划列出可能的情况加以分析
1.考虑当 i =1的时候
(1)j<p(i):肯定是零
(2)j>=p(i):他也肯定是一,因为这时最优解里面是空的,不用考虑香蕉🍌
2.考虑当 i>1时
(1)j<p(i):这时肯定还是不能包含这一条导线的,因为这一条导线的下接线柱没有被包含前 j 个里面。
那么这时他就相当于dp[i-1][j]。 为什么这么说呢?因为在j<p(i)时这一条导线是不可能被包含在我们的最优解里面的,所以就相当与这一条导线(i 导线)对于我们的当前的解是没有任何作用的。他就相当于是前 i -1个上接线柱和前 j 个下接线柱构成的问题的最优解。
也许此时聪明好学的你会问那为什么不是dp[i-1][j-1]呢?(即为什么不是前 i -1个上接线柱和前 j -1 个下接线柱构成的问题的最优解呢?。)
此时我们直接举一个一针见血的例子,如果i-1的下接线柱是 j 呢?dp[i-1][j-1]是不是就把第i-1条导线给漏掉了。
(2)j>=p(i): 这时候就说明我们可以包含这个导线,注意我说的是可以包含而不是一定包含。那么包含的条件是什么呢?想必你肯定已经知道了,就是当这条导线与最优解里面的导线都不香蕉🍌的时候 且 包含这个导线的最优解的个数比不包含这条导线的个数要大的时候才会包含 (dp[i][j]=Math.max(dp[i-1][p[i]-1]+1,dp[i-1][j])) 。而相交的时候就不可以包含了(dp[i][j]=dp[i-1][j])。
最优子结构
1.对与i<1的时候肯定是满足的,因为他的子问题不就是空的集合吗。
2.对于i>1的时候
(1)j<p(i) 它的最优解所包含的导线个数是是子问题的最优解dp[i-1][j]。假设子问题的最优解不是dp[i-1][j]而是R那么R>dp[i-1][j]所以原问题的最优解应该是R,这就矛盾了。
(2)j>=p(i) 的时候他的子问题是选择这一条导线(dp[i-1][p[i]-1]+1)或则不选这一条导线(dp[i][j]=dp[i-1][j])这两个中的最大值。对于不选择和上面的证明是一样的。
这里证明一下选择的情况:
在证明之前先了解一下子问题为什么是这个集合(前i-1个上接线柱,前p[i]-1个下接线柱)而不是其他的集合(例如前i-1个上接线柱,前j个下接线柱)。
我们既然选择了这一个导线就说明这个导线是不会与最优解里面的导线相交的。dp[i-1][p[i]-1]是前i-1个上接线柱,前p[i]-1个下接线柱 组成的解。我们的这一条导线对应的接线柱是i和p[i]。i>i-1且p[i]>p[i]-1所以他是这个集合中的最后一条线。就好比上图中的前4条导线,4是最后一条所以他肯定不
会与前三条相交的。
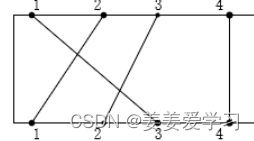
**那又为什么是j-1呢而不是其他的呢?**因为上接线柱是前i-1条,那么就算下接线柱不是j-1是j+1那么是不是就相交了呢
差不多理解了,就来证明最优子结构:
如果dp[i-1][p[i]-1]不是子问题的最优,最优的是R那么R+1>dp[i-1][p[i]-1]+1,所以由子问题构成的原问题的最优解应该是R+1而不是dp[i-1][p[i]-1]
代码
import java.util.Scanner;public class AD {public static void MSN(int n,int[] p,int[][] dp){for(int i=1;i<=n;i++){for (int j=1;j<=n;j++){if(i<=1){if(j<p[i]){dp[i][j]=dp[i-1][j];}else {dp[i][j]=1;}}else {if(j<p[i]){dp[i][j]=dp[i-1][j];}else {dp[i][j]=Math.max(dp[i-1][p[i]-1]+1,dp[i-1][j]);}}}}
}public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n=scanner.nextInt();int[] p=new int[n+1];p[0]=0;for(int i=1;i<=n;i++){p[i]=scanner.nextInt();}int[][] dp=new int[n+1][n+1];// System.out.println(dp[n][n]);MSN(n,p,dp);System.out.println(dp[n][n]);}
}相关文章:

电路布线问题动态规划详解(做题思路)
对于电路布线问题,想必学过动态规划的大家都很清除。今天就来讲解一下这个动态规划经典题目。 目录 问题描述输入分析最优子结构代码 问题描述 在一块电路板的上、下2端分别有n个接线柱。根据电路设计,要求用导 线(i,π(i))将上端接线柱与下端接线柱相…...

webpack 的 Loader 和 Plugin 的区别,常见的 loader 和 plugin 有哪些?
结论先行: 1、 Loader 和 Plugin 的区别 Loader 也叫做就是“加载器”,因为 webpack 原生只能解析 js 文件,而对于其他类型文件,则需要借助 loader。所以 loader 的作用就是实现对不同格式文件的解析和处理,例如把 E…...
云计算实战项目之---学之思在线考试系统
简介: 学之思开源考试系统是一款 java vue 的前后端分离的考试系统。主要优点是开发、部署简单快捷、界面设计友好、代码结构清晰。支持web端和微信小程序,能覆盖到pc机和手机等设备。 支持多种部署方式:集成部署、前后端分离部署、docker部…...
)
研究生学术与职业素养讲座MOOC---期末复习(1-15)
目录 单选题多选题填空题判断题 单选题 我国制造科学与技术与工业发达国家相比的阶段性差距不包括:人工成本高不属于面向产业的学科:哲学哪个国际前沿本讲未提:纳米技术早期的科学研究不分学科是以达芬奇为例说的待遇不是管理者与领导者的区…...

kube-prometheus-stack监控k8s1.24+ docker缺少图像
1.24 中 cAdvisor 指标中缺少图像、名称和容器标签 由于 Kubernetes 1.24 已经从 cadvisor 中删除了 docker 插件,因此虽然可以使用 cri-dockerd 来适配容器运行时,但 cadvisor 无法获取有关图像标签等 docker 容器信息。进而导致 grafana 很多图像无数据。解决方法为对 pro…...

【C/PTA——循环结构3】
C/PTA——循环结构3 7-1 二分法求多项式单根1.题目要求2.代码实现 7-2 循环-十进制转化1.题目要求2.代码实现 7-3 梅森数1.题目要求2.代码实现 7-4 单词长度1.题目要求2.代码实现 7-5 21循环-求和31.题目要求2.代码实现 7-6 21循环-金字塔1.题目要求2.代码实现 7-7 循环-杨辉三…...

MAC设备(M1)环境下编译安装openCV for Java
最近发现一个需求,可以用openCV来实现,碰巧又新买了mac笔记本,就打算利用业余时间安装下openCV。这里将主要步骤记录下,希望能帮助有需要的人。 1、准备编译环境 #查询编译opencv相关依赖 brew info opencv查询结果如下图所示&a…...
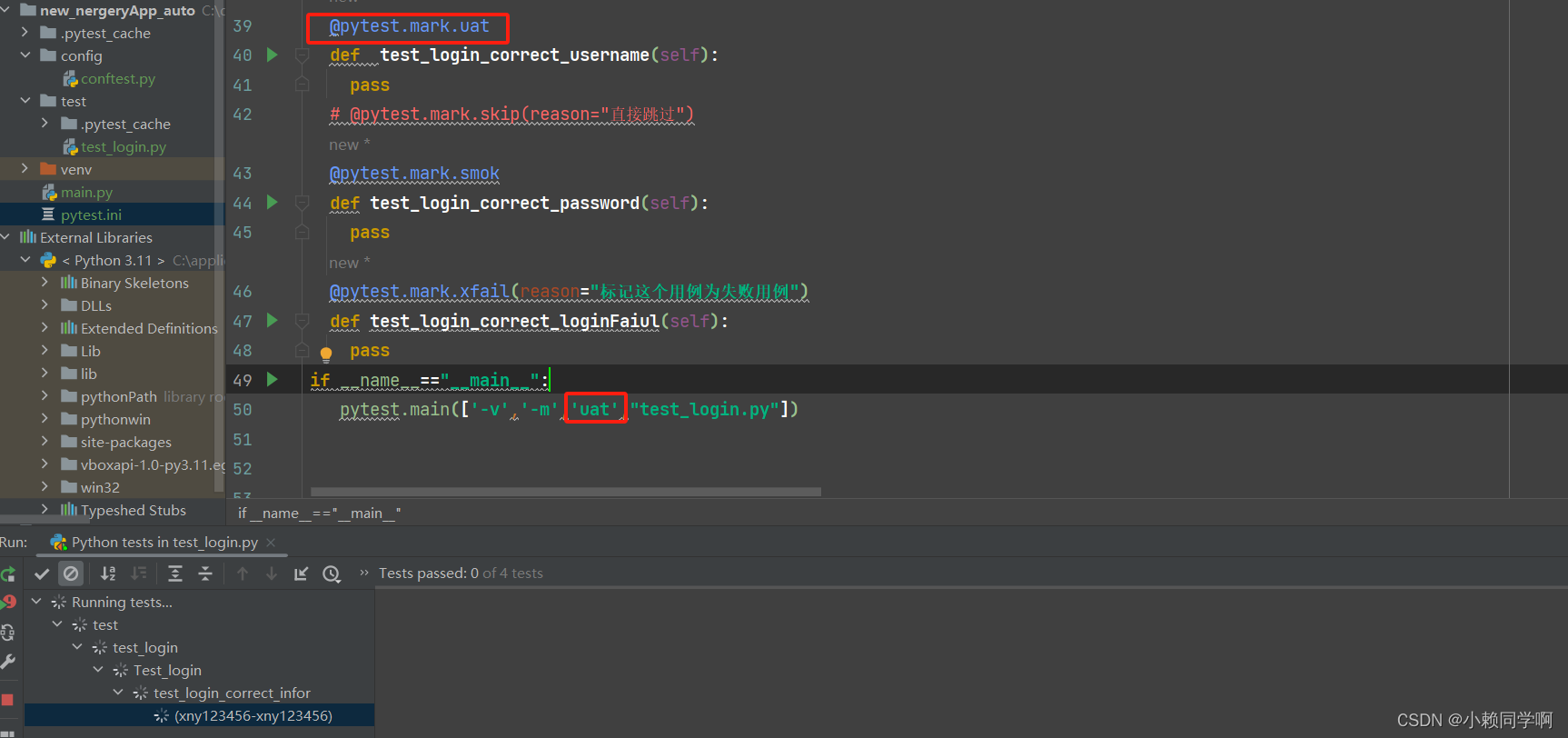
pytest中的pytest.ini
[pytest] filterwarnings ignore::DeprecationWarning addopts -v -s markers uat:1 smok:2 log_cli1 xfail_strict True filterwarnings ignore::DeprecationWarning 这个的功能就是 test_login.py::Test_login::test_login_correct_password PASSEDwarnings summary …...

C#通过TCP发送List<string>
using System; using System.IO; using System.Net.Sockets; using System.Text; using System.Collections.Generic;public static void SendList<string>(Stream stream, List<string> list) {// 将List<string>对象转换为字节数组byte[] data Encoding.U…...

Mactracker for mac(硬件信息查询工具)免费下载
想知道你电脑的信息吗?Mactracker Mac版是Macos上一款硬件信息查询工具,可以查询电脑中的硬件信息,还可以查看您使用软件的具体情况,苹果电脑产品和周边产品的信息,售价等等,让您对电脑有更多深刻的了解。 …...
MES管理系统中常规的生产建模有哪些
随着制造业的快速发展,MES生产管理系统已经成为了现代制造业不可或缺的核心系统。MES通过对生产过程进行建模,实现了生产过程的可视化、可控制和可优化,为企业提供了全方位的生产管理解决方案。本文将深化对MES管理系统及其主要生产模型的理解…...

电商API:淘宝京东拼多多1688多电商平台的商品销量库存信息获取
item_get 获得淘宝商品详情 获取APIkeyitem_get_pro 获得淘宝商品详情高级版item_review 获得淘宝商品评论item_fee 获得淘宝商品快递费用item_password 获得淘口令真实urlitem_list_updown 批量获得淘宝商品上下架时间seller_info 获得淘宝店铺详情item_search 按关键字搜索淘…...
EPLAN软件中的术语-主数据‘’技术分享
在EPLAN中,主数据(Master Data)这个词被经常、反复地提及,我曾经困惑了很长时间,不得要领。在EPLAN的帮助系统中,它列举了一部分内容,说这些这些就是主数据,但没有解释什么是主数据,除了上面这些…...
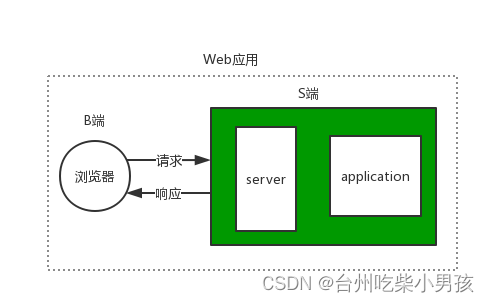
web应用程序、Django框架的学习
web应用程序 什么是web? Web应用程序是一种可以通过Web访问的应用程序,用户只需要有浏览器即可,不需要再安装其他软件 案例: 淘宝网、京东网、博客园、等都是基于web应用的程序 应用程序有两种模式C/S、B/S。C/S是客户端/服务器端程序,…...

【c++之设计模式】组合使用:抽象工厂模式与单例模式
简介 学以致用,使用抽象工厂及单例模式创建不同轿车及轿车装饰品。 代码 定义一个抽象工厂类来创建不同类型的轿车和轿车装饰品。抽象工厂类中具有创建不同类型轿车和轿车装饰品的纯虚方法。 abstractFactory.h #pragma once#include "Car.h" #inclu…...
Adobe Photoshop Elements 2024 v24.0 简体中文版 | 中文直装版
下载: http://dt1.8tupian.net/2/29913a53b500.pg3介绍:Photoshop Elements 2024(简称PSE即PS简化版)是一款定位在数码摄影领域的全新的图像处理软件,该软件包括了专业版的大多数特性,只有少量的简化选项,提供了调整颜…...
seata事务回滚引起的skywalking数据库存储空间剧增的问题排查
基本信息 产品名称:ATS3.0 问题分类:编码问题 环境类型:环境无关 问题现象 11月1日上午华润DBA收到数据库磁盘空间告警,检查后发现skywalking连接的mysql数据库占用空间从之前一直是比较稳定的,但是10月31日…...

数据库SQL
数据库&SQL 数据库基本概念数据库DataBase定义 数据库管理系统(DBMS)定义在JAVA项目中与数据库的结合数据库管理系统中常见的概念库与表的关系 SQL数据类型数字类型浮点类型字符类型TEXT类型日期类型 SQL语言的分类DDL:数据定义语言修改表结构的注意事项 DML:数据操作语言D…...
C语言实现给一个不多于5位的正整数,要求:一、求它是几位数,二、逆序打印出各位数字。
完整代码: // 给一个不多于5位的正整数,要求:一、求它是几位数,二、逆序打印出各位数字。 #include<stdio.h>int main(){int num;int len0;printf("请输入一个不多于5位的正整数:");scanf("%d",&n…...

101 对称二叉树
原题链接:101 对称二叉树 全代码: /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : va…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

EC2安装WebRTC sdk-c环境、构建、编译
1、登录新的ec2实例,证书可以跟之前的实例用一个: ssh -v -i ~/Documents/cert/qa.pem ec2-user70.xxx.165.xxx 2、按照sdk-c demo中readme的描述开始安装环境: https://github.com/awslabs/amazon-kinesis-video-streams-webrtc-sdk-c 2…...

JavaScript性能优化实战大纲
性能优化的核心目标 降低页面加载时间,减少内存占用,提高代码执行效率,确保流畅的用户体验。 代码层面的优化 减少全局变量使用,避免内存泄漏 // 不好的实践 var globalVar I am global;// 好的实践 (function() {var localV…...

SpringBoot3中使用虚拟线程的详细过程
在 Spring Boot 3 中使用 Java 21 的虚拟线程(Virtual Threads)可以显著提升 I/O 密集型应用的并发能力。以下是详细实现步骤: 1. 环境准备 JDK 21:确保安装 JDK 21 或更高版本Spring Boot 3.2:最低要求(p…...
