ModStart系统安全规范建议
1 不要使用弱密码
很多人为了系统管理方便(或者是懒),经常会设置类似 123456、admin 这样的管理密码,这样的密码很容易被暴力软件扫描出来。
2 不要使用默认配置
默认的软件系统设置、默认的系统端口、默认的网站设置在发生漏洞时都可能在第一时间被不法人员利用,修改掉系统默认的配置可以很大程度避免这样的风险。
3 最小权限原则
最小权限,也就是在给一个软件权限时,避免使用 root 这样的权限,这样可以很大程度上保证系统发生漏洞时整个操作系统受到威胁。同时,不同的软件在配置数据库时,使用不同的用户名进行隔离,这样可以避免一个网站被攻击所有网站遭殃的悲剧。
4 多网站隔离
通常情况,一个服务器都是会搭建多个网站来共用相同的 PHP 配置,在搭建系统时,应尽可能的将不同的网站进行隔离,这样可以避免一个网站被攻击时,其他网站也会受到影响。推荐采用 docker 这样的虚拟化技术来实现。
5 不使用来源不明的系统
网站经营者经常经常会在不同的网站上下载一些来源不明的系统进行安装,这样的系统很可能被不法分子恶意的留后门,会造成极大的威胁。应该要从正规渠道采购、下载正版软件,避免这样的悲剧发生。
6 请专业的技术维护
很多站长都是身兼数职,不可能在技术的所有领域都精通,因此很可能会造成因配置不当造成的安全事故。我们在实际运营过程中也会遇到说 “是不是你们的系统有漏洞导致我们服务器被攻击”。作为系统开发者,我们进我们所能规范技术开发来最大程度的保证用户的系统安全,但是再安全的系统如果因为服务器配置不当也会出现很严重的安全事故,因此如果条件允许,请专业的人来维护网站是一个不错的选择。
XSS介绍与预防
举例:用户提交数据时如果填写 Hello<script>alert('hello');</script>,当系统处理数据时过滤不完全,就会出现 XSS 漏洞,用户的代码就会被执行。
可以通过以下几种方式预防:
1 输入过滤
过滤所有用户输入的数据,默认可以使用 HtmlUtil::filter 进行富文本过滤)
2 显示转义
在 blade 页面渲染数据时通常有两种方式,如果内容中可能含有 xss 内容,需要过滤或者使用第一种
## 第一种,会把 < > 等特殊字符转换为实体字符
{{ $xxx }}
## 第二种,会原样输出,不对字符进行转换
{!! $xxx !!}
#3 X-Frame-Options
防止网页被嵌套
攻击者可以使用一个透明的、不可见的iframe,覆盖在目标网页上,然后诱使用户在该网页上进行操作,此时用户将在不知情的情况下点击透明的iframe页面。通过调整iframe页面的位置,可以诱使用户恰好点击iframe页面的一些功能性按钮上,导致被劫持。
生产环境的网站都会添加防盗链,不希望自己网页页面被其他站的 FRAME 嵌套进去, 这时候就需要的HTTP协议头里增加X-Frame-Options这一项。
DENY表示该页面不允许在 frame 中展示,即便是在相同域名的页面中嵌套也不允许。SAMEORIGIN表示该页面可以在相同域名页面的 frame 中展示。ALLOW-FROM "https://example.com/"表示该页面可以在指定来源的 frame 中展示。
Nginx参考
add_header X-Frame-Options DENY;
add_header X-Frame-Options SAMEORIGIN;
add_header X-Frame-Options "ALLOW-FROM https://xxx.xxxxxx.com http://example.com";
1
2
3
Apache参考
Header always append X-Frame-Options SAMEORIGIN
1
#4 Content-Security-Policy
内容安全策略
CSP 的实质就是白名单制度,开发者明确告诉客户端,哪些外部资源可以加载和执行,等同于提供白名单。它的实现和执行全部由浏览器完成,开发者只需提供配置。CSP 大大增强了网页的安全性。攻击者即使发现了漏洞,也没法注入脚本,除非还控制了一台列入了白名单的可信主机。
详细参考:http://www.ruanyifeng.com/blog/2016/09/csp.html(opens new window)
如配置限定script执行,可参考配置
Nginx参考
add_header Content-Security-Policy 'script-src \'self\' \'unsafe-inline\' \'unsafe-eval\' a.example.com b.example.com; report-uri https://example.com/csp_report;';
可配合使用 FELoggerServer (opens new window)模块来记录非法 script 请求
Nginx 配置漏洞 alias 别名漏洞
nginx在配置别名(alias)时,将“/files” 等同为“/home/”,可以看到这里多了一个“/”,这个就导致可从/home/目录穿越到他的上层目录,即 /files../ == /home/../ ,其错误配置示例如下:
location /files {alias /home/;
}相关文章:

ModStart系统安全规范建议
1 不要使用弱密码 很多人为了系统管理方便(或者是懒),经常会设置类似 123456、admin 这样的管理密码,这样的密码很容易被暴力软件扫描出来。 2 不要使用默认配置 默认的软件系统设置、默认的系统端口、默认的网站设置在发生漏洞…...
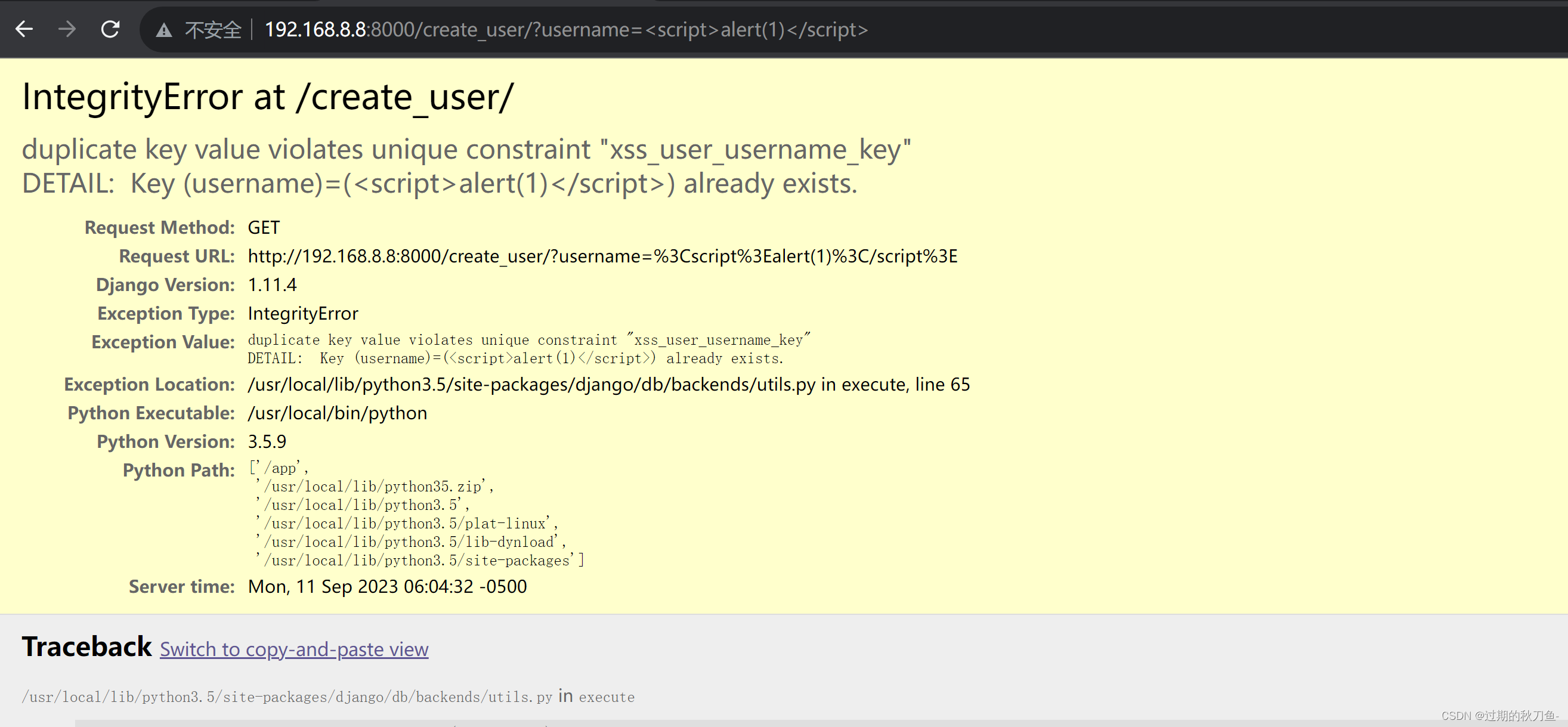
【漏洞复现】Django_debug page_XSS漏洞(CVE-2017-12794)
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞分析3、漏洞验证 说明内容漏洞编号CVE-2017-12794漏洞名称Django_debug page_XSS漏洞漏洞评级影响范…...

Redis性能调优:深度剖析与示例解析
标题:Redis性能调优:深度剖析与示例解析 引言 Redis是一款强大的开源内存数据库,广泛应用于高性能系统。然而,为了充分发挥Redis的性能,需要进行合理的性能调优。本博客将深入介绍Redis性能调优的策略和示例…...

oracle查询前几条数据的方法
在Oralce中实现select top N:由于Oracle不支持select top 语句,所以在oracle中经常是用order by 跟rownum的组合来实现select top n的查询。 方法1: SELECT * FROM (SELECT * FROM EMP ORDER BY SAL DESC) WHERE ROWNUM < 5 --抽取处记录…...

c#弹性和瞬态故障处理库Polly
1. 重试(Retry) Policy .Handle<Exception>() //指定需要重试的异常类型 .Retry(2,(ex,count,context)> { //指定发生异常重试的次数Console.WriteLine($ "重试次数{count},异常{ex.Message}" ); }) …...

20231107-前端学习炫酷菜单效果和折叠侧边栏
炫酷菜单效果 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>炫酷菜单效果</title><…...
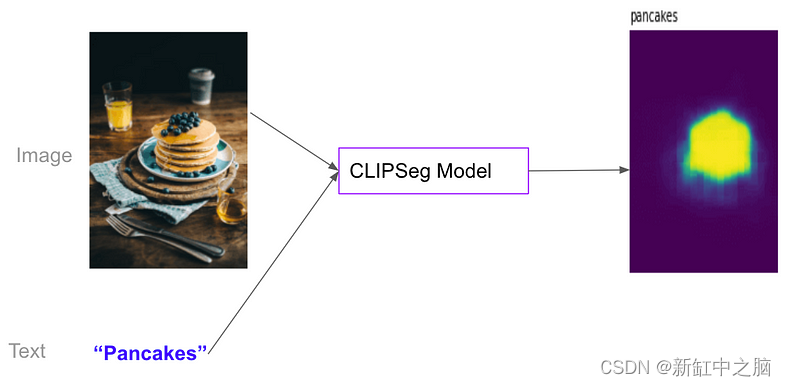
基于CLIP的图像分类、语义分割和目标检测
OpenAI CLIP模型是一个创造性的突破; 它以与文本相同的方式处理图像。 令人惊讶的是,如果进行大规模训练,效果非常好。 在线工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 3D…...

python爬虫(数据获取——selenium)
环境测试 from selenium import webdriverchromedriver_path r"C:\Program Files\Google\Chrome\Application\chromedriver.exe" driver webdriver.Chrome()url "https://www.xinpianchang.com/discover/article?fromnavigator" driver.get(url)drive…...

[wp]NewStarCTF 2023 WEEK5|WEB
前言:比赛是结束了,但我的学习还未结束,看看自己能复习几道题吧,第四周实在太难 Final 考点: ThinkPHP 5.0.23 RCE一句话木马上传SUID提权(find) 解题: 首先页面就给了ThinkPHP V5, 那无非考…...

未将对象引用设置到对象实例
环境 vs 2017 qt 5.13.0 qt-vs-addin 2.10 qt 项目打开的vs 2010 的项目 配置完成之后可以编译执行,但是新建qt 类提示 未将对象引用设置到对象实例 问题 插件的版本太高了使用低版本的,到qt 官网下载Index of /official_releases/vsaddin 下载q…...
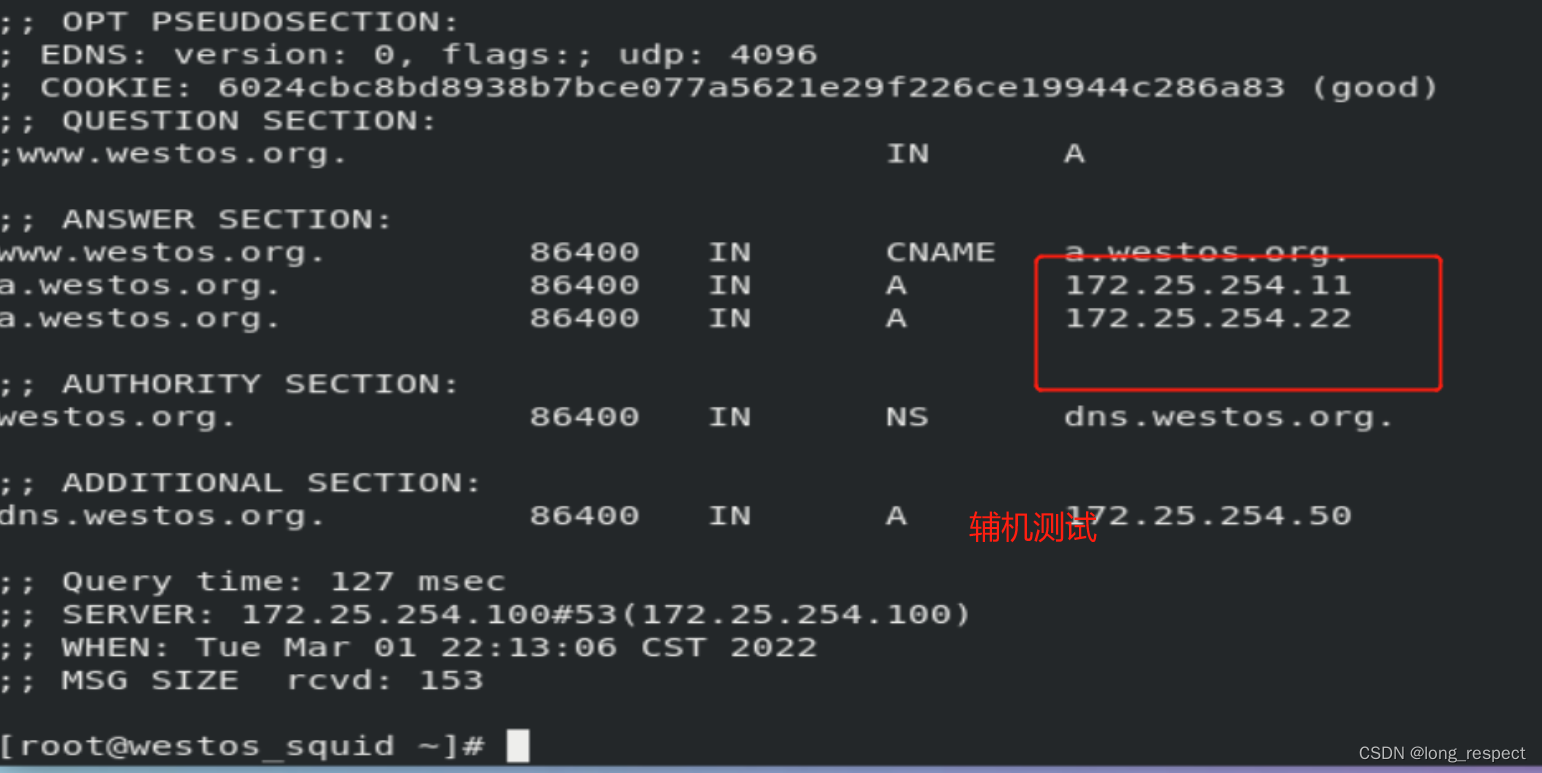
网络的地址簿:Linux DNS服务的全面指南
1 dns 1.1 dns(域名解析服务)介绍 当访问 www.baidu.com 首先查询/etc/hosts,如果没有再去查询/etc/resolv.conf,还是没有就去查询域名服务器 关于客户端: /etc/resolv.conf ##dns指向文件 nameserver 172.25.254.20测试&…...

输电线路AR可视化巡检降低作业风险
随着现代工业的快速发展,各行业的一线技术工人要处理的问题越来越复杂,一些工作中棘手的问题迫切需要远端专家的协同处理。但远端专家赶来现场往往面临着专家差旅成本高、设备停机损失大、专业支持滞后、突发故障无法立即解决等痛点。传统的远程协助似乎…...
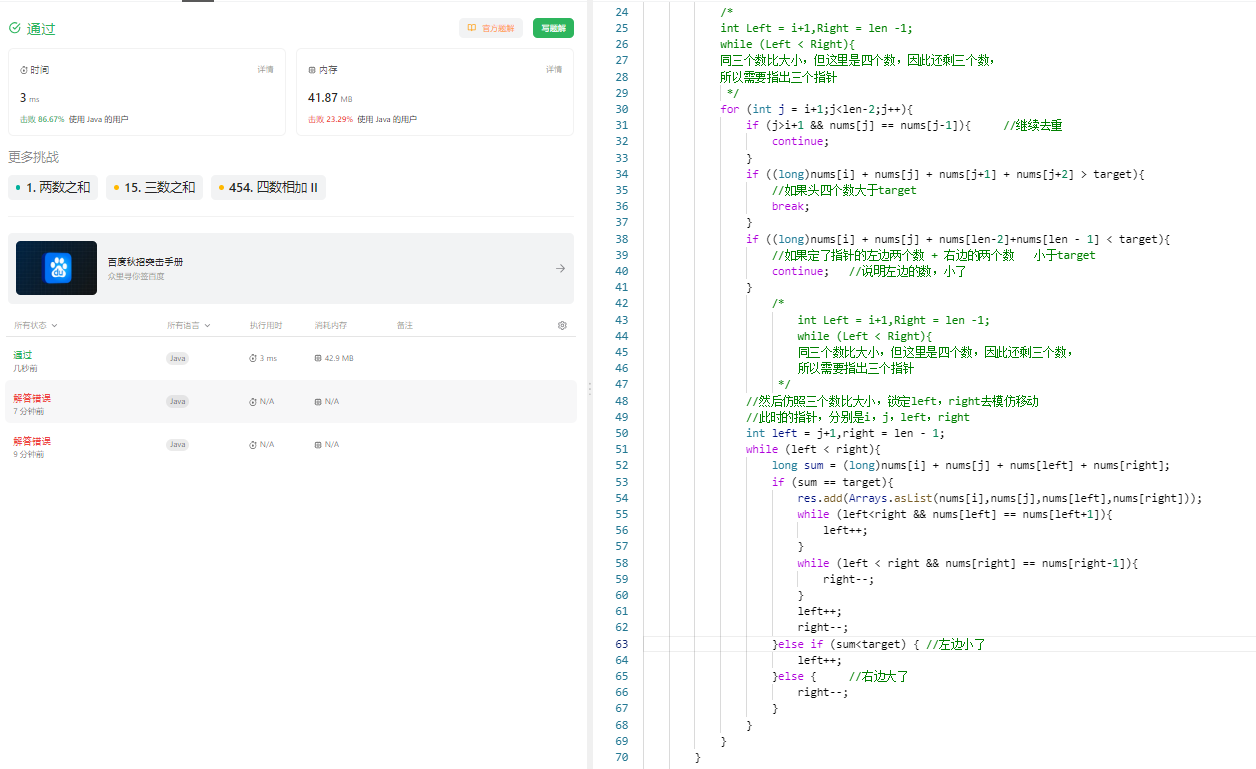
18. 四数之和
18. 四数之和 原题链接:完成情况:解题思路:参考代码:错误经验吸取 原题链接: 18. 四数之和 https://leetcode.cn/problems/4sum/description/ 完成情况: 解题思路: /** * //HashMap只能记录…...

排序:堆排序(未完待续)
文章目录 排序一、 排序的概念1.排序:2.稳定性:3.内部排序:4.外部排序: 二、插入排序1.直接插入排序 二、插入排序堆排序 排序 一、 排序的概念 1.排序: 一组数据按递增/递减排序 2.稳定性: 待排序的序列…...
小米智能电视投屏方法
小米智能电视也提供了投屏功能。 使用遥控器,在应用中找到它,点击进入。 小米电视支持windows笔记本,macbook笔记本,iphone手机,安卓手机投屏。 windows笔记本投屏 在投屏应用中找到windows投屏,选中开…...
,或者受委托司法所审查。)
保外就医罪犯收到指定医院《罪犯病情诊断书》及检测、检查报告等其他医疗文书后,应当在规定时限内提交( ),或者受委托司法所审查。
需要查看详细试题题库及其参考答案的,请到(题-海-舟)里进行搜索查看。可搜试题题干或者搜索关键词,搜题的时候,先进行题目识别,能大大提高学习效率,感谢使用! 保外就医罪犯收到指定…...

pytorh模型训练、测试
目录 1 导入数据集 2 使用tensorboard展示经过各个层的图片数据 3 完整的模型训练测试流程 使用Gpu训练的两种方式 使用tensorboard显示模型 模型训练测试 L1Loss函数 保存未训练模型或者已经训练完的模型 4 加载训练好的模型进行测试 1 导入数据集 import torch from torch.u…...
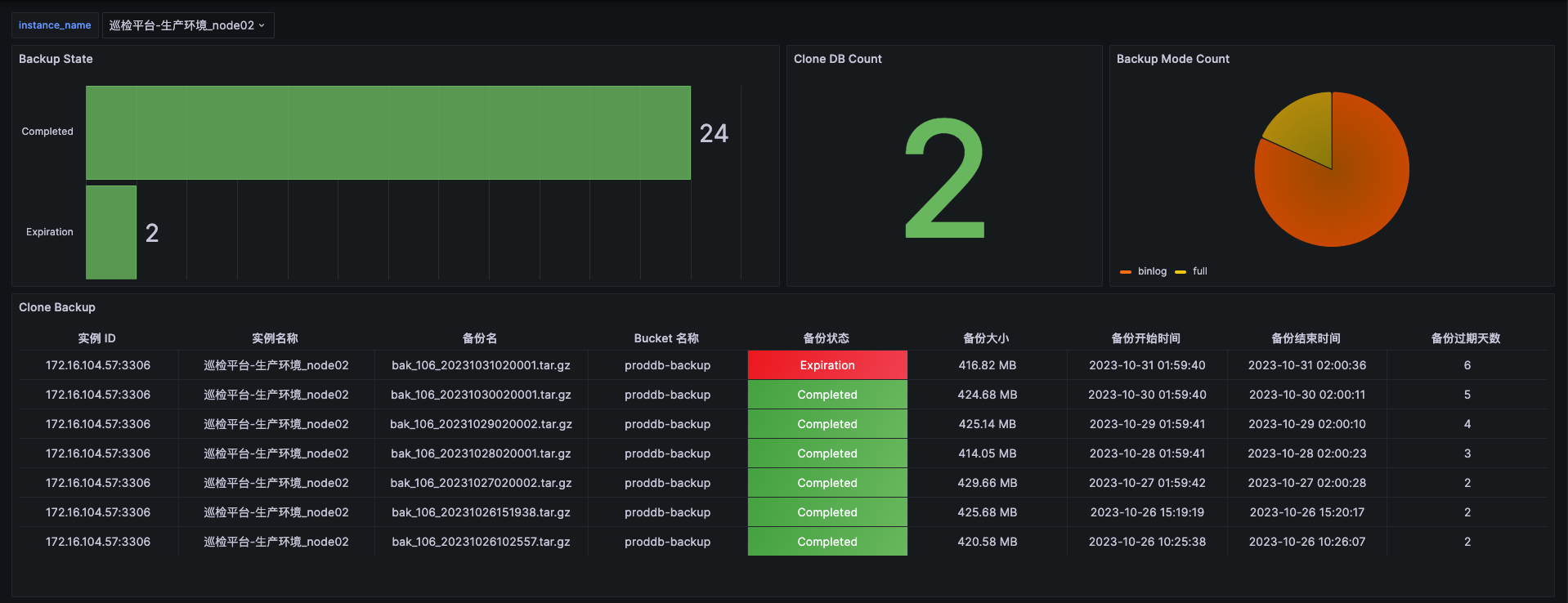
MySQL 8.0 Clone Plugin 详解
文章目录 前言1. 克隆插件安装2. 克隆插件的使用2.1 本地克隆2.2 远程克隆 3. 克隆任务监控4. 克隆插件实现4.1 Init 阶段4.2 File Copy4.3 Page Copy4.4 Redo Copy4.5 Done 5. 克隆插件的限制6. 克隆插件与 Xtrabackup 的异同7. 克隆插件相关参数 后记 前言 克隆插件…...

掌握未来技术趋势:深度学习与量子计算的融合
掌握未来技术趋势:深度学习与量子计算的融合 摘要:本博客将探讨深度学习与量子计算融合的未来趋势,分析这两大技术领域结合带来的潜力和挑战。通过具体案例和技术细节,我们将一睹这两大技术在人工智能、药物研发和金融科技等领域…...

京东数据分析:2023年9月京东笔记本电脑行业品牌销售排行榜
鲸参谋监测的京东平台9月份笔记本电脑市场销售数据已出炉! 9月份,笔记本电脑市场整体销售下滑。鲸参谋数据显示,今年9月份,京东平台上笔记本电脑的销量将近59万,环比下滑约21%,同比下滑约40%;销…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
