学习笔记|Pearson皮尔逊相关系数|Spearman斯皮尔曼相关系数|和Kendall肯德尔tau-b相关系数|分析流程|-SPSS中双变量相关性分析系数
目录
- 学习目的
- 软件版本
- 原始文档
- 基础概念
- 皮尔逊相关系数
- 基本假设(适用条件):
- 系数的范围及意义
- 实例
- 1. 读数据:
- 2.正态性检验:
- 3.异常值检验(体重):
- 4.分析:
- 斯皮尔曼相关系数
- 基本假设(适用条件):
- 肯德尔tau-b相关系数
- 基本假设(适用条件):
- 相关性系数的比较
- 皮尔森相关与Spearman和Kendall相关
- Spearman相关与Kendall相关
学习目的
SPSS中双变量相关性分析系数
软件版本
IBM SPSS Statistics 26。
原始文档
三个相关系数的注意事项
Pearson/Spearman/Kendallta三大相关系数怎么选?怎么计算?
《小白爱上SPSS》课程第18讲数据
Statistical functions (scipy.stats)包-scipy.stats.pearsonr
Statistical functions (scipy.stats)包-scipy.stats.spearmanr
Statistical functions (scipy.stats)包-scipy.stats.kendalltau
百度百科:spearman相关系数
相关性检验-Kendall’s Tau-b相关系数
Pearson’s Correlation 皮尔逊相关性分析详细操作
基础概念
皮尔逊相关系数
Pearson相关系数是传统的统计分析工具,应用广泛。Pearson相关系数公式:

但其有明显的理论局限,即只能度量线性的相关性,隐含地做了高斯性假设(正态分布、独立性假、方差齐性),使其无法在非线性和非高斯的情况下应用。
基本假设(适用条件):
每个观察值应具有一对值。比较的两个变量必须来源于同一个总体。
每个变量应该是连续的。
每个变量应为正态分布。
应该没有异常值。
系数的范围及意义
皮尔逊相关系数的范围是位于[-1,1]之间。相关系数展示了方向性:
如果相关系数接近1,说明两个变量之间呈较高的正相关性;
如果相关系数接近-1,说明两个变量之间呈较高的负相关性;
如果相关系数接近0,说明两个变量之间彼此独立,没有相关性。
实例
1. 读数据:
GET FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第十八讲:线性相关分析.sav'.
2.正态性检验:
EXAMINE VARIABLES=体重 肺活量/PLOT HISTOGRAM NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
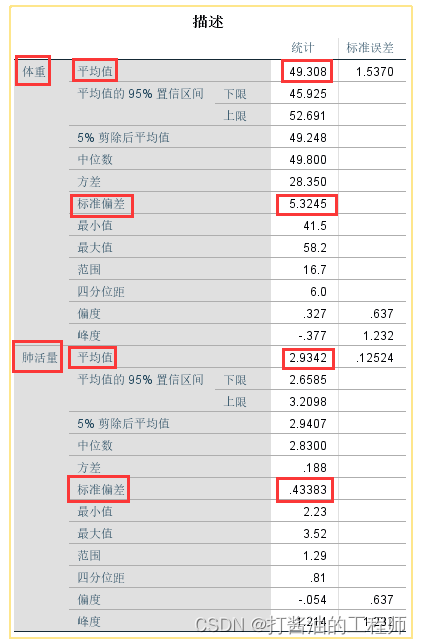
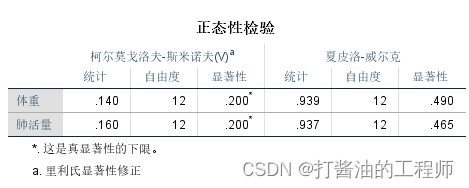
经S-W(夏皮洛-威尔克)检验,体重、肺活量数据的p值分别为0.490和0.465,均大于0.05,无统计学意义,支持原假设,可认为两组数据符合正态分布。
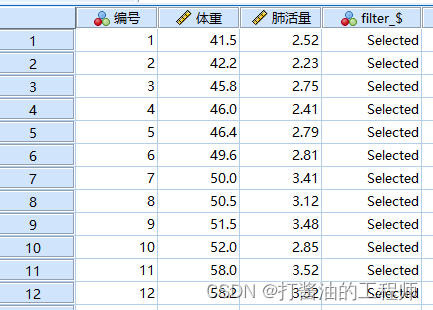
3.异常值检验(体重):
USE ALL.
COMPUTE filter_$=(体重 <= (49.308+3*5.3245) & 体重 >= (49.308-3*5.3245)).
VARIABLE LABELS filter_$ '体重 <= (49.308+3*5.3245) & 体重 >= (49.308-3*5.3245) (FILTER)'.
VALUE LABELS filter_$ 0 'Not Selected' 1 'Selected'.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.
无异常值:

异常值检验(肺活量):
USE ALL.
COMPUTE filter_$=(肺活量 <= (2.9342+3*.43383) & 肺活量 >= (2.9342-3*.43383)).
VARIABLE LABELS filter_$ '肺活量 <= (2.9342+3*.43383) & 肺活量 >= (2.9342-3*.43383) (FILTER)'.
VALUE LABELS filter_$ 0 'Not Selected' 1 'Selected'.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.
无异常值:
4.分析:
CORRELATIONS /VARIABLES=体重 肺活量 /PRINT=TWOTAIL NOSIG /*显著性检验:双尾*//STATISTICS DESCRIPTIVES /*选项中选定:平均值、标准偏差*//MISSING=PAIRWISE /*皮尔逊*/.
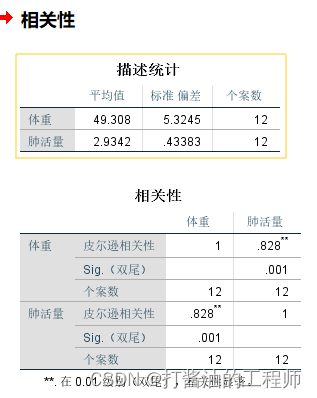
皮尔逊相关性分析结果显示,P值显著性为0.001。P值小于0.05,说明示例的两个变量相关。相关性系数为0.828,离1比较近,也说明呈较高的正相关性。
斯皮尔曼相关系数
斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数。
对于样本容量为n的样本,n个原始数据被转换成等级数据,相关系数ρ为:

斯皮尔曼相关系数表明X(独立变量)和Y(依赖变量)的相关方向。如果当X增加时,Y趋向于增加,斯皮尔曼相关系数则为正。如果当X增加时,Y趋向于减少,斯皮尔曼相关系数则为负。斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。当X和Y越来越接近完全的单调相关时,斯皮尔曼相关系数会在绝对值上增加。当X和Y完全单调相关时,斯皮尔曼相关系数的绝对值为1。完全的单调递增关系意味着任意两对数据Xi,Yi和Xj,Yj,有Xi−Xj和Yi−Yj总是同号。完全的单调递减关系意味着任意两对数据Xi,Yi和Xj,Yj,有Xi−Xj和Yi−Yj总是异号。
斯皮尔曼相关系数经常被称作"非参数"的。这里有两层含义。首先,当X和Y的关系是由任意单调函数描述的,则它们是完全皮尔逊相关的。与此相应的,皮尔逊相关系数只能给出由线性方程描述的X和Y的相关性。其次,斯皮尔曼不需要先验知识(也就是说,知道其参数)便可以准确获取XandY的采样概率分布。
基本假设(适用条件):
两对数据的观察是独立的。
应按序数,区间或比率测量两个变量。
假定两个变量之间存在单调关系。
皮尔逊Pearson相关系数使用前提条件中,任何一个条件不满足时可以考虑使用该系数;
Spearman与Pearson相关系数计算很类似,只是Spearman计算需要将两个变量转化为序数。
肯德尔tau-b相关系数
Kendall’s Tau相关系数,是由英国统计学家Maurice Kendall于1938年提出,主要包括Somers’ D、Goodman-kruskal’s gamma(γ)、Kendall’s Tau(a、b、c)等一系列相关系数。其中,最常用的是Kendall’s Tau-b和Kendall’s Tau-c相关系数。Kendall’s Tau相关系数适用于判断两列离散有序型数据之间的相关性,本文主要讲解Kendall’s Tau-b相关系数的计算。

基本假设(适用条件):
假设同spearman。但适应条件和前两者比完全不一样,衡量有序分类型数据的序数相关性。
相关性系数的比较
皮尔森相关与Spearman和Kendall相关
非参数相关(指 spearman和hendall)的表达能力相对较弱,因为它们在计算中使用的信息较少。在Pearson的情况下,相关性使用有关均值和均值偏差的信息,而非参数相关性仅使用序数信息和成对分数。
在非参数相关的情况下,X和Y值可能是连续的或有序的,并且不需要X和Y的近似正态分布。但在皮尔逊相关的情况下,它假定X和Y的分布应该是正态分布,并且也应该是连续的(因此做spearman之前要做一些对数变换之类的尽量接近正态分布)。
相关系数 测量线性(皮尔逊)或单调(Spearman和Kendall)关系。
Spearman相关与Kendall相关
在正常情况下,Kendall相关性比Spearman相关性更强健和有效。这意味着当样本量较小或存在一些异常值时,首选Kendall相关。
在所有情况下,Kendall相关系数的绝对值均小于其他绝对值。 可以看出,肯德尔相关性比其他相关性更为保守。
相关文章:

学习笔记|Pearson皮尔逊相关系数|Spearman斯皮尔曼相关系数|和Kendall肯德尔tau-b相关系数|分析流程|-SPSS中双变量相关性分析系数
目录 学习目的软件版本原始文档基础概念皮尔逊相关系数基本假设(适用条件):系数的范围及意义实例1. 读数据:2.正态性检验:3.异常值检验(体重):4.分析: 斯皮尔曼相关系数基…...

计算机服务器中了locked勒索病毒怎么办,勒索病毒解密,数据恢复
随着网络技术的不断成熟,网络中存在的病毒威胁也不断增多,近期,云天数据恢复中心陆续接到很多企业的求助,企业的计算机服务器数据库遭到了勒索病毒攻击,并且勒索病毒的攻击与加密形式也发生了许多变化。其中攻击次数较…...

本地生活餐饮视频怎么拍摄能有更多流量?如何批量生产呢?
本地生活近几年特别的火,所以到现在各类内容雷同性也比较高,视频缺少新的创意和玩法,像餐饮店的视频,大部分都是拍顾客进门、拍餐饮店座无虚席的实景……作为用户,其实早就已经看腻了。 今天推荐本地生活餐饮店商家拍…...
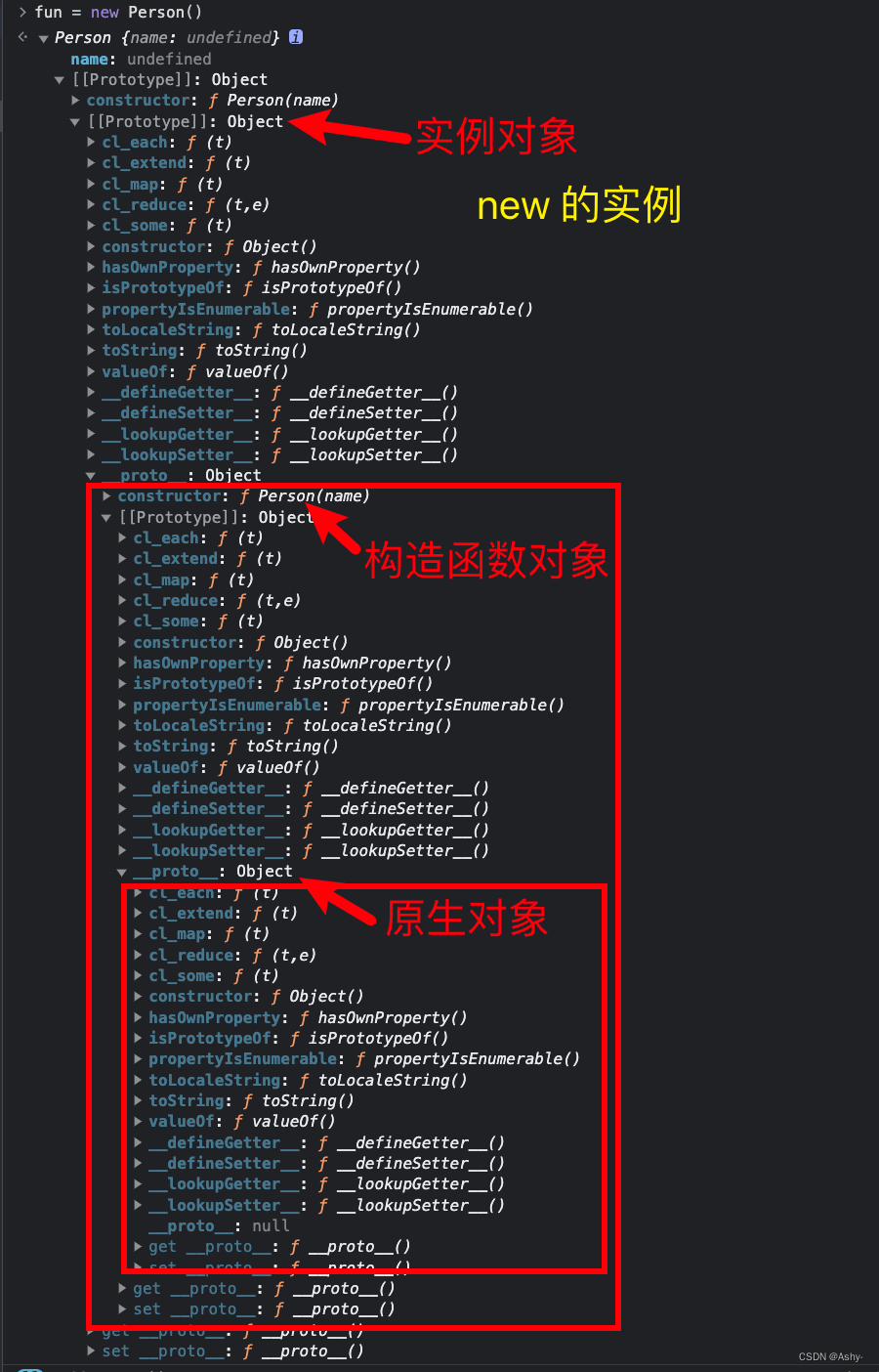
【笔记】原型和原型链(持续完善)
概念 原型:函数都具有 prototype 属性,称之为原型,也称之为原型对象 1.1 原型可以放一些属性和方法,共享给实例对象使用(也就是原生方法)。 1.2 原型可以做继承原型链:对象都有 __proto__ 属性…...

python向word中添加表格
1、表格插入 方法一:直接创建表添加 #导入库 from docx import Document #创建文档对象 document Document()#创建5行7列表格 table document.add_table(rows5, cols7)#修改第2行第3列单元格的内容为中国 table.cell(1,2).text中国 #修改第3行第4列单元格的内容…...
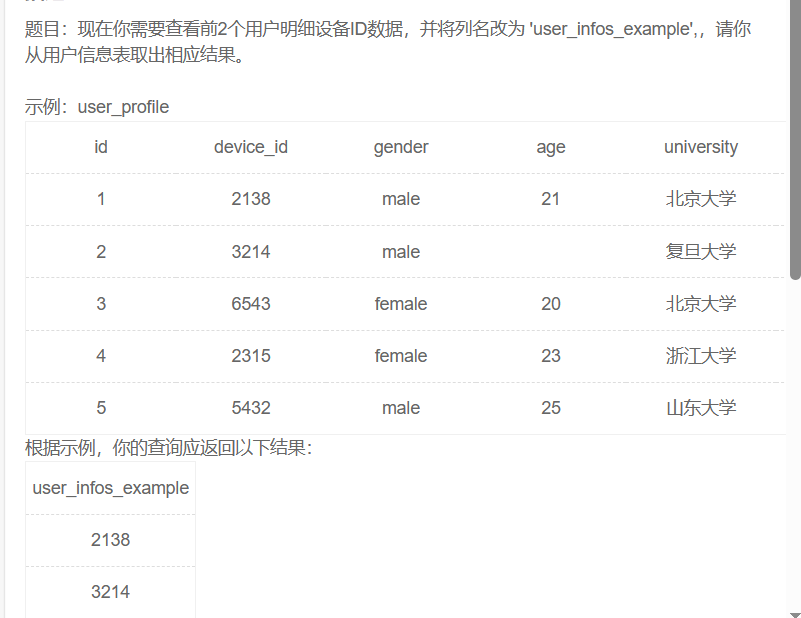
2023_11_6 每日半小时 SQL 刷题
文章目录 1. 查询所有列题目描述SQL 语句编写 2. 查询多列题目描述SQL 语句编写 3. 查询结果去重题目描述SQL 语句编写 4. 查询结果限制返回行数题目描述SQL 语句编写 5. 将查询后的列重新命名题目描述SQL 语句编写 语法小总结 1. 查询所有列 题目链接:SQL1 查询所…...
Redis系列-Redis性能优化与安全【9】
目录 Redis系列-Redis性能优化与安全【9】Redis性能优化策略Redis安全设置与防护措施Redis监控与诊断工具介绍 七、Redis应用案例与实战八、Redis未来发展与趋势 个人主页: 【⭐️个人主页】 需要您的【💖 点赞关注】支持 💯 Redis系列-Redis性能优化与安…...
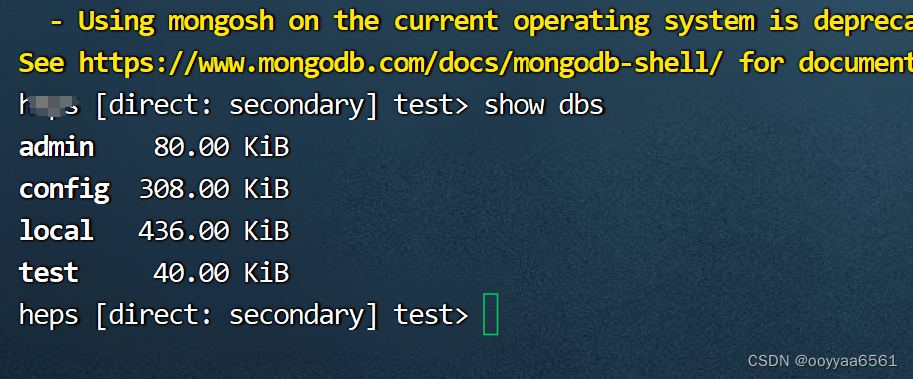
centos7下安装主从仲裁三台结构的MongoDB 7.0.4
安装手册英文版在这里 https://www.mongodb.com/docs/v7.0/tutorial/install-mongodb-on-red-hat/ 我的安装过程 1)基础安装 1、创建 /etc/yum.repos.d/mongodb-org-7.0.repo文件 下面的代码复制到这个文件中,保存 [mongodb-org-7.0] nameMongoDB Re…...

2258. 逃离火灾 : 详解如何从「二分」到「分类讨论」(图解过程)
题目描述 这是 LeetCode 上的 「2258. 逃离火灾」 ,难度为 「困难」。 Tag : 「多源 BFS」、「二分」、「预处理」 给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid,它表示一个网格图。 每个格子为下面 个值之一: 0 表示草地。 1 表…...

基于SSM框架的共享单车管理系统小程序系统的设计和实现
基于SSM框架的共享单车管理系统小程序系统的设计和实现 源码传送入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码传送入口 前言 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,…...
COOHOM通过采用亚马逊云科“专库专用”的方式,为云原生的构建提供稳定的数据支撑
全球化浪潮下,面对全球化业务发展带来的新需求与新挑战,越来越多的企业开启了云原生构建旅程,以推动业务系统快速迭代,为国际业务的拓展打下坚实的基础。COOHOM是杭州群核信息技术有限公司旗下的国际化品牌。为全球企业和个人提供…...
Java根据一个List内Object的两个字段去重
背景 在Java开发过程中,我们经常会遇到需要对List进行去重的需求。 其中常见的情况是,将数组去重,或者将对象依据某个字段去重。这两种方式均可用set属性进行处理。 今天讨论,有一个List,且其中的元素是自定义的对象&…...

运维那些事儿|2023年,运维还有出路吗?
作为一名运维,不知道你有没有这样的感受。 觉得自己的工作没什么成长空间。每天装个系统、跑个机房、跑个脚本,忙来忙去也没忙出来什么名堂,含金量低不说,薪资也一直没见涨,所以你开始陷入迷茫,会疑惑&…...
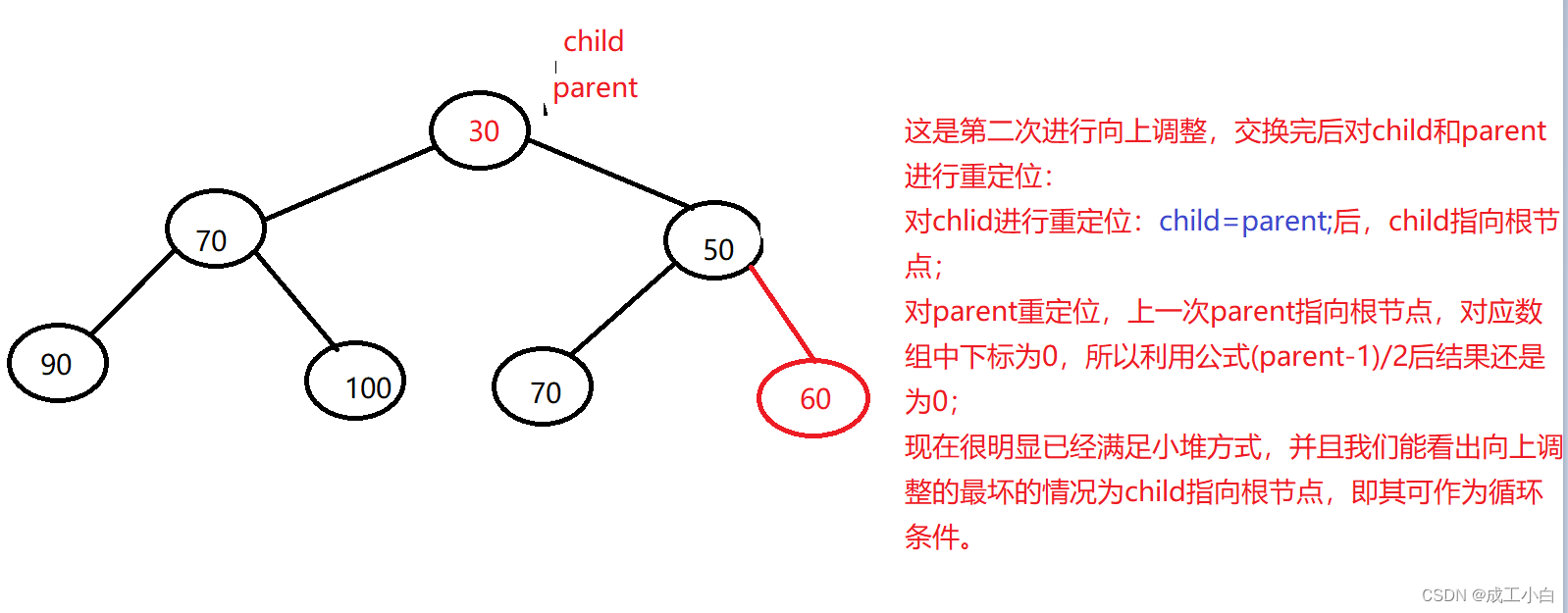
数据结构——二叉树(2)
接上一篇文章http://t.csdnimg.cn/nsKsW,本次我们接着讲解关于二叉树的相关知识。 一、二叉树的相关性质: 1. 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2^(i-1) 个结点. 2. 若规定根节点的层数为 1 ,则 深度…...
aosp定制android系统
目录 AOSP 准备工作(配置) 确定机型和版本 初始化 git安装 curl安装 同步源码 环境变量 创建aosp目录 指定同步版本 解下来安装编译需要的依赖 编译aosp源码 刷入系统 AOSP 全称 Android Open Source Project 是指Android开源项目,它是由Google主导的…...

程序员的护城河:构建数字世界的守护者
目录 前言1 持续学习的愿望和能力2 与他人沟通和合作的能力3 追求技术的深度和广度4 具备分享的精神结语 前言 在数字化时代,程序员是现代社会的护城河。他们的工作不仅是构建应用程序和系统,更是为保障系统安全、数据防护以及网络稳定发挥着至关重要的…...

Sample Average Approximation,SAA
1. sample average approximation,SAA “样本平均近似”(Sample Average Approximation,SAA)方法是数学优化和运筹学领域广泛使用的优化技术。它主要用于处理优化问题的目标函数或约束涉及随机或不确定参数的情况。SAA尤其适用于具有随机或概…...
springbootMysql文华学院青年志愿者服务预约系统97973-计算机毕业设计项目选题推荐(附源码)
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 文华学院青年志愿者服务预约系统,主要的模块包括管理员:后台首页、轮播图、通知公告管理、资源管理(新闻资…...

Go 语言向函数传递数组
Go 语言向函数传递数组 在 Go 语言中,数组是值类型,因此将数组传递给函数时,将复制整个数组。如果数组非常大,这可能会导致性能问题。为了避免复制整个数组,可以通过传递切片(Slice)来传递数组…...

高压放大器在铁电测试中的用途有哪些
高压放大器在铁电测试中有多种重要用途。铁电材料是指具有自发极化的晶体材料,具有一系列特殊的电学和物理性质。铁电测试是研究铁电材料性质的关键实验手段之一。下面安泰电子将介绍高压放大器在铁电测试中的几个主要用途。 极化场施加:铁电材料的最显著…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
