Sample Average Approximation,SAA
1. sample average approximation,SAA
“样本平均近似”(Sample Average Approximation,SAA)方法是数学优化和运筹学领域广泛使用的优化技术。它主要用于处理优化问题的目标函数或约束涉及随机或不确定参数的情况。SAA尤其适用于具有随机或概率性特性的问题。以下是SAA方法的概述,以及它的用途、优势和劣势:
1. 方法概述:
SAA是一种基于模拟的优化技术,它通过使用从不确定参数的概率分布中抽取的场景样本来逼近目标函数的期望值。其主要思想是用有限样本的经验平均值替代期望值。这使得优化问题可以重新表述为一个确定性优化问题,从而更容易处理。
2. 用途:
SAA通常用于各种应用领域,包括但不限于:
-
随机规划:SAA经常用于随机规划中,以解决不确定性下的决策问题。示例包括供应链管理、金融和能源生产,其中需求、价格或其他因素可能会随机变化。
-
风险管理:SAA可用于优化风险度量,如风险价值(Value at Risk,VaR)或条件风险价值(Conditional Value at Risk,CVaR),在金融和投资组合优化中应用广泛。
-
工程和设计:它用于工程和设计问题,其中参数(如材料性质、负载或环境条件)存在不确定性。
-
库存和生产计划:SAA有助于在需求不确定的情况下优化库存和生产计划。
3. 优势:
-
多功能性:SAA可应用于各种具有随机或不确定参数的问题,使其成为不确定情况下决策制定的多功能工具。
-
确定性形式:SAA将随机问题转化为确定性问题,可以使用传统的优化技术来解决。这简化了问题,允许使用现有的优化求解器。
-
灵活性:SAA可以适应各种概率分布和抽样技术,因此适用于不同的问题设置。
-
效率:与替代方法相比,SAA可以在相对较小的场景数量下提供合理的近似值,降低了计算复杂性。
4. 劣势:
-
样本大小:SAA解的质量取决于场景样本的大小。小样本可能导致不准确的逼近,而大样本可能计算代价高昂。
-
收敛问题:SAA不一定总是收敛到随机问题的真正最优解,尤其是在目标或约束高度非线性的情况下。
-
偏差:如果场景样本不代表真正的概率分布,SAA可能引入偏差。需要仔细抽样以减轻这个问题。
-
维度问题:在高维问题中,SAA可能面临挑战,因为为了准确表示分布,所需场景数量会随维度呈指数增长。
总之,"样本平均逼近"方法是在不确定情况下优化决策制定中有价值的工具,具有多功能性、简单性和效率的优势。然而,它也有与样本大小、收敛、偏差和维度问题相关的限制。研究人员和从业者通常需要精心设计和分析SAA解决方案,以确保其在解决特定的随机优化问题时有效。
2. 常用的采样方法
“样本平均逼近”(Sample Average Approximation,SAA)方法中,采样方法是关键的组成部分,它用于生成从不确定参数的概率分布中抽取的场景样本。不同的采样方法可以用来获得这些场景样本,具体选择取决于问题的性质和计算资源。以下是一些常见的采样方法:
-
蒙特卡洛采样:蒙特卡洛方法是一种常见的采样方法,它使用随机数生成器从概率分布中生成场景样本。这是一种非参数方法,通常用于连续分布。它可以是简单的随机抽样或更复杂的方法,如马尔可夫链蒙特卡洛(MCMC)。
-
拉丁超立方采样:这种采样方法旨在提高采样的均匀性,以减少估计的方差。它通过在参数空间内创建均匀分布的点来生成场景样本。
-
抽头法(Latin Hypercube Sampling,LHS):LHS是一种改进的采样方法,它在均匀分布的点之间添加一些随机性,以更好地代表概率分布。
-
逆变换采样:逆变换法使用概率分布的累积分布函数(CDF)的反函数来生成随机样本。这适用于分布具有已知CDF的情况。
-
重要性采样:重要性采样是一种用于减小方差的技术,它选择样本,使那些对于估计目标具有更高重要性的样本更有可能被选中。
-
分段采样:对于分段概率分布,可以使用分段采样方法,分别在不同的分段内采样,然后根据每个分段的权重对样本进行加权。
-
马尔可夫链蒙特卡洛(MCMC):MCMC方法使用马尔可夫链来生成样本,通常应用于复杂的概率分布,如贝叶斯推断问题。著名的MCMC算法包括Metropolis-Hastings和Gibbs采样。
-
剧本生成:在某些应用中,可以使用特定领域的模型来生成场景样本。例如,气象模型可以用于生成天气预测场景。
选择合适的采样方法通常取决于问题的特性、概率分布的形状以及计算资源的可用性。在"样本平均逼近"方法中,重要的是确保采样方法能够生成具有代表性的场景样本,以便在估计期望值或解决随机优化问题时获得准确的结果。
3.蒙特卡洛采样的概率分布怎么获得呢
蒙特卡洛采样的概率分布通常是根据已知的概率密度函数(Probability Density Function,PDF)或累积分布函数(Cumulative Distribution Function,CDF)来获得的。这意味着你需要知道随机变量的分布类型以及相关的参数。以下是一些步骤,可用于从已知的概率分布获取样本:
-
了解随机变量的分布类型:首先,你需要了解你所处理的随机变量的概率分布类型。常见的分布包括正态分布、均匀分布、指数分布、伽玛分布等。分布的选择取决于问题的特性和数据的性质。
-
获取分布的参数:一旦你知道分布类型,就需要获取相关的分布参数,如均值、方差、形状参数等。这些参数将决定分布的具体形状。
-
生成随机数:使用随机数生成器,你可以生成符合所选分布的随机数。常见的编程语言(如Python、R和MATLAB)都提供了内置的随机数生成函数,可用于生成符合各种分布的随机数。
-
应用蒙特卡洛采样:使用生成的随机数作为蒙特卡洛采样的样本点。你可以根据问题需求采集多个样本,这些样本将代表所选分布。
具体步骤可以根据你所使用的编程语言和库而有所不同。下面是一个示例,使用Python和NumPy库生成符合正态分布的随机数:
import numpy as np# 定义正态分布的参数
mu = 0 # 均值
sigma = 1 # 标准差# 生成随机数样本
sample_size = 1000 # 样本大小
random_samples = np.random.normal(mu, sigma, sample_size)
在上面的示例中,np.random.normal函数生成了符合均值为mu,标准差为sigma的正态分布的随机数样本。你可以根据问题的需求调整分布类型和参数,并生成适当分布的随机数。
4. SAA采样的样本量是怎么确定的?
确定SAA(Sample Average Approximation)采样的样本量通常需要在问题的具体背景下进行考虑,并且涉及到折中和计算资源。样本量的大小会影响SAA近似的准确性和计算的效率。以下是一些考虑样本量的一般原则:
-
准确性需求: 样本量的大小取决于你对问题解的准确性的需求。通常来说,样本量越大,SAA的近似结果越接近真实值。如果你需要更高的准确性,可能需要更大的样本量。
-
问题复杂度: 问题的复杂度也会影响样本量的选择。更复杂的问题通常需要更多的样本才能获得可接受的准确性。
-
计算资源: 样本量的选择还受到计算资源的限制。如果计算时间和计算能力有限,你可能需要在准确性和计算效率之间进行权衡。较小的样本量可能会降低计算成本,但也可能导致近似的不够准确。
-
收敛性检验: 你可以使用一些收敛性检验方法来确定样本量是否足够。例如,你可以开始使用相对较小的样本量,然后逐渐增加样本量,观察近似解是否在稳定,不再显著变化。
-
专业经验: 领域专业知识和经验也可以指导样本量的选择。在某些情况下,领域专家可能能够提供关于样本量的有用建议。
总的来说,确定SAA采样的样本量通常需要进行试验和调整,以便在满足问题准确性需求的同时,保持计算效率。开始时,你可以选择一个适度的样本量,然后根据实验结果进行调整,以找到满足你的需求的最佳样本量。这个过程可能需要反复迭代,以获得满意的结果。
相关文章:

Sample Average Approximation,SAA
1. sample average approximation,SAA “样本平均近似”(Sample Average Approximation,SAA)方法是数学优化和运筹学领域广泛使用的优化技术。它主要用于处理优化问题的目标函数或约束涉及随机或不确定参数的情况。SAA尤其适用于具有随机或概…...
springbootMysql文华学院青年志愿者服务预约系统97973-计算机毕业设计项目选题推荐(附源码)
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 文华学院青年志愿者服务预约系统,主要的模块包括管理员:后台首页、轮播图、通知公告管理、资源管理(新闻资…...

Go 语言向函数传递数组
Go 语言向函数传递数组 在 Go 语言中,数组是值类型,因此将数组传递给函数时,将复制整个数组。如果数组非常大,这可能会导致性能问题。为了避免复制整个数组,可以通过传递切片(Slice)来传递数组…...

高压放大器在铁电测试中的用途有哪些
高压放大器在铁电测试中有多种重要用途。铁电材料是指具有自发极化的晶体材料,具有一系列特殊的电学和物理性质。铁电测试是研究铁电材料性质的关键实验手段之一。下面安泰电子将介绍高压放大器在铁电测试中的几个主要用途。 极化场施加:铁电材料的最显著…...
一款高效、简洁的数据处理和清洗加工工具,值得收藏!
随着数字化时代的快速发展,数据已经成为企业运营和决策的重要依据。然而,处理和分析大量复杂数据是一个具有挑战性的任务,特别是在数据清洗和加工环节。为了满足这一需求,JVS-BI提供了一套高效、简洁的数据处理和分析解决方案。 …...
很多个pdf怎么合并在一起?
很多个pdf怎么合并在一起?作为一个办公室的伙伴,对于PDF格式肯定不会陌生。它强大的功能为我们的工作提供了许多便利。由于PDF文件格式的稳定性和安全性较高,我们通常在工作或学习中使用它来传输文件,很多人都喜欢将办公文件都做成…...

Ubuntu apt更换国内镜像源,apt 更新源,apt 国内镜像
详细一篇: https://midoq.github.io/2022/05/30/Ubuntu20-04%E6%9B%B4%E6%8D%A2%E5%9B%BD%E5%86%85%E9%95%9C%E5%83%8F%E6%BA%90/ 更换方法 Ubuntu采用apt作为软件安装工具,其镜像源列表记录在/etc/apt/source.list文件中。 首先将source.list复制为s…...

时序预测 | MATLAB实现WOA-CNN-BiLSTM-Attention时间序列预测(SE注意力机制)
时序预测 | MATLAB实现WOA-CNN-BiLSTM-Attention时间序列预测(SE注意力机制) 目录 时序预测 | MATLAB实现WOA-CNN-BiLSTM-Attention时间序列预测(SE注意力机制)预测效果基本描述模型描述程序设计参考资料 预测效果 基本描述 1.MAT…...

VINS-Mono-后端优化 (一:预积分残差计算-IMU预积分约束)
这里先回顾一下预积分是怎么来的 VINS-Mono-IMU预积分 (三:为什么要预积分预积分推导) 这里贴出预积分的公式 具体含义解释看对对应的文章 整个误差函数如下 预积分 α \alpha α β \beta β γ \gamma γ 是用 IMU 预积分获得的增量&a…...
怎么调整excel表里面所有单元格中,某个相同字体大小,单元格中其他文字大小不变?
环境: excel 2021 python3.8 问题描述: 怎么调整excel表里面所有单元格里面1这个字体大小,单元格里面其他文字不变? excel表里面。很多单元格都有1,1和文字都是10号字体,现在想把全部1字字体调整为16号其他字大小都不变 解决方案: 一、使用python来实现,经过测…...

流式数据库引擎备受关注,亚信安慧AntDB数据库受邀参加“2023中国PostgreSQL数据库生态大会”
11月3日至5日,2023中国PostgreSQL数据库生态大会在北京中科院软件所大报告厅盛大召开,大会现场百余位专家学者、企业、用户代表及线上数千位观众,就近年来国产数据库技术与市场变革进行深入探讨。湖南亚信安慧科技有限公司(简称&a…...
)
kafka开启SSL认证(包括内置zookeeper开启SSL)
zookeeper和kafka的SSL开启都可单独进行 生成SSL证书 使用jre自带的keytool工具生成,linux和windows下生成的证书可以通用 生成含有一个私钥的keystore文件,有效期10年(本文证书密码统一使用test123) keytool -genkeypair -ali…...
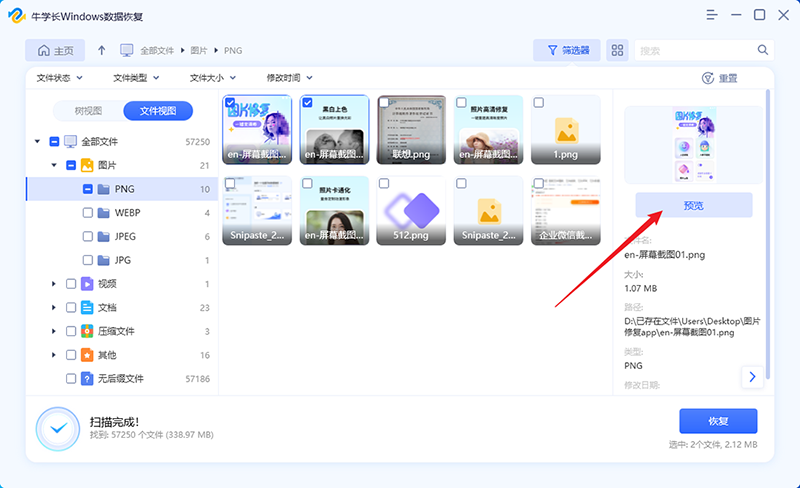
Powerpoint不小心被覆盖?PPT误删文件如何恢复?
PowerPoint不小心删除了,这可能是众多学生和工作人员最头痛的事情了。PPT被覆盖或误删可能意味着几个小时的努力付之东流。那么PPT覆盖的文档要如何救回来呢?小编将会在本篇文章中为大家分享几个解决方案,使PPT文档覆盖还原操作成为可能&…...

美团产品经理面试题大解密:流量VS口碑,如何找到最佳平衡点?
大家好,我是你们的小米。最近我参加了一场美团的产品经理面试,其中一个问题让我颇为犯愁:“产品应该追求高流量还是高口碑?”这个问题困扰了很多产品经理,因为两者似乎都对产品的成功有着重要影响。今天我就来和大家一…...
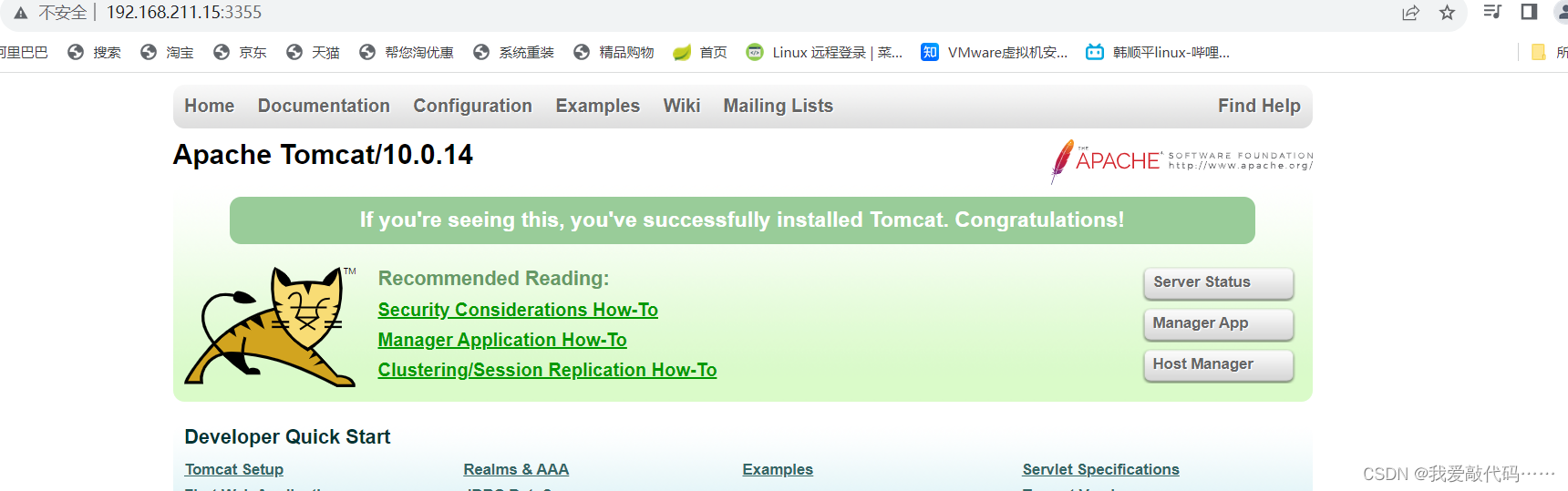
docker部署tomcat
1.下载tomcat镜像 尽量去下载最新版本 直接输入docker pull tomcat 后面不跟版本号(要是跟版本号,你还要去官网去查看是否有此版本,太麻烦了) 2.查看镜像 3.通过镜像去run启动容器 -d 就是后台运行 --name 给容器取个新名字 -p 3355:8080…...

大语言模型(LLM)综述(七):大语言模型设计应用与未来方向
A Survey of Large Language Models 前言8 A PRACTICAL GUIDEBOOK OF PROMPT DESIGN8.1 提示创建8.2 结果与分析 9 APPLICATIONS10 CONCLUSION AND FUTURE DIRECTIONS 前言 随着人工智能和机器学习领域的迅速发展,语言模型已经从简单的词袋模型(Bag-of-…...
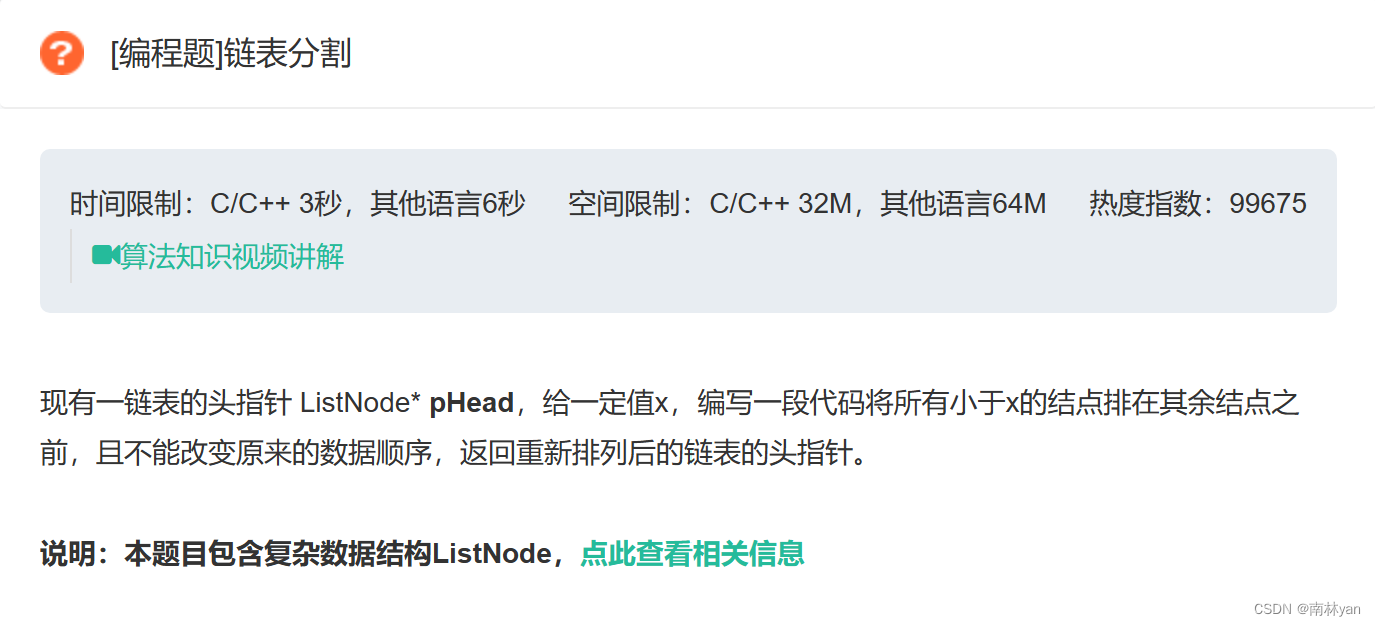
牛客网:链表分割
一、题目 函数原型: ListNode* partition(ListNode* pHead, int x) 二、思路 根据题意,可以设置两个新的链表,将原链表中所有小于x的结点链接到链表1中,大于x的结点链接到链表2中,最后再将两个链表合并即可。 此题有两…...
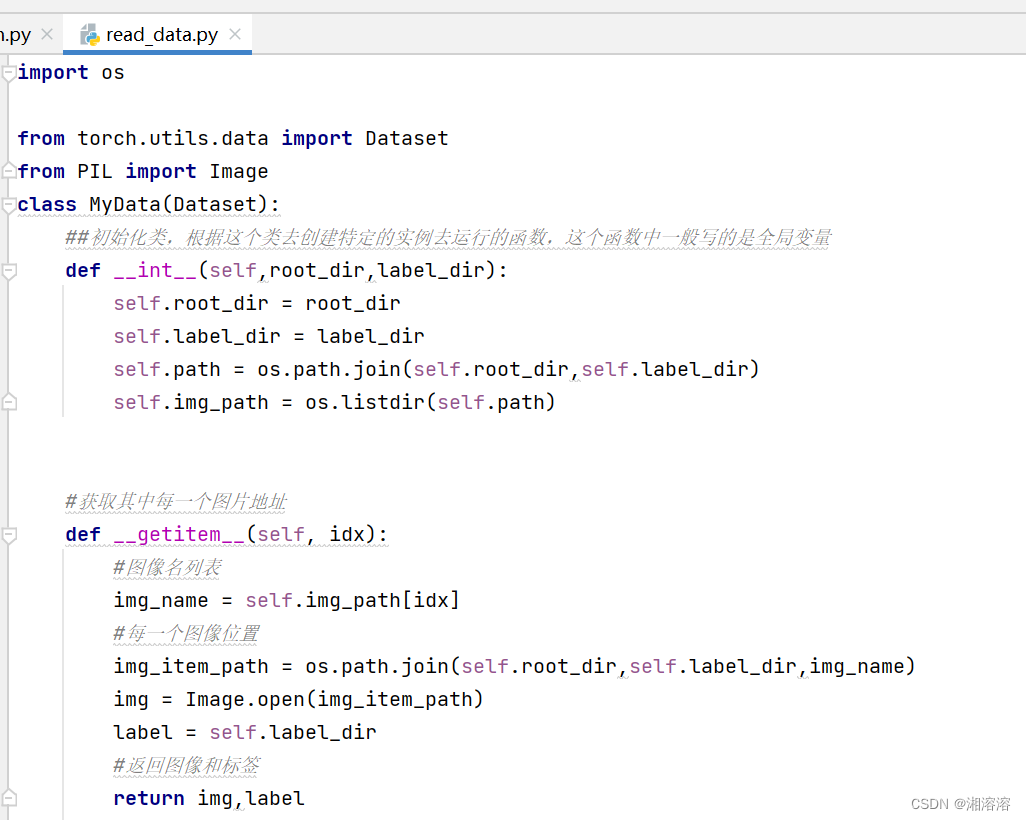
pytorch(小土堆)深度学习
第五节课讲项目的创建和对比 第六节:Dataset,Dataloader Dataset提供一种方式区获取数据及其label(如何获取每一个数据及其label,告诉我们总共有多少的数据) Dataloader为后面的网络提供不同的数据形式 第七节:Dataset类代码实战 显示图片 f…...

统计 boy girl 复制出来多少次。 浴谷 P1321题
统计 boy girl 复制出来多少次。 #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <iomanip>void fun(char* s) {int boy 0, girl 0;int t 0;while (*s) {if (t 0 && *s!.) {t 1;if (*s b || *s o || *s y)boy 1;elsegirl 1;}…...

odoo16前端框架分析1 boot.js
odoo16前端框架分析1 boot.js odoo16的前端基于owl组件系统,这是一个类似vue,react的现代js框架。 前端框架都放在了web模块中,具体的位置是addons/web/static/src 不过今天要说的不是owl,而是跟前端启动有关的几个重要文件 1、…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
