很多个pdf怎么合并在一起?
很多个pdf怎么合并在一起?作为一个办公室的伙伴,对于PDF格式肯定不会陌生。它强大的功能为我们的工作提供了许多便利。由于PDF文件格式的稳定性和安全性较高,我们通常在工作或学习中使用它来传输文件,很多人都喜欢将办公文件都做成pdf格式。然而,当面临文件过多、上传不便或查找麻烦等问题时,我们可以采用合并PDF文件的方法来解决。将多个PDF文件合并成一个后,我们可以轻松地将其发送给同事或朋友,他们接收到后阅读也更加方便。那么今天的问题就引申出来了,你知道用什么方法和合并pdf文件吗?
虽然pdf文件现在大家使用的比较多,但毕竟pdf不是office办公文件,很多人对于pdf文件的使用仅限于阅读,但并没有真正编辑或者处理过pdf文件,你会发现新想要合并pdf文件并不简单,这需要外部的软件工具进行帮助才能完成。相信很多人看到这篇文章时正在寻找相关教程,那么小编就为大家详细介绍一下pdf文件合并的详细步骤。

pdf合并的方法一:使用“优速PDF工厂”软件进行合并
步骤1,相信大家也是第一次听说“优速PDF工厂”这个软件吧,所以我们准备工作就是将它下载到电脑上并安装好,大家可以在百度里搜索名称进行下载,也可以直接通过下载链接进行下载。

步骤2,安装好之后打开使用,首页上可以看到3个选项,我们点击右边的【PDF文件操作】选项。
步骤3,此时进入了软件内页,我们点击软件左边列表下的【PDF合并】功能;然后点击【添加文件】按钮或者用鼠标拖拽的方式,将需要合并的pdf文件添加到软件中,文件数量没有限制哦。
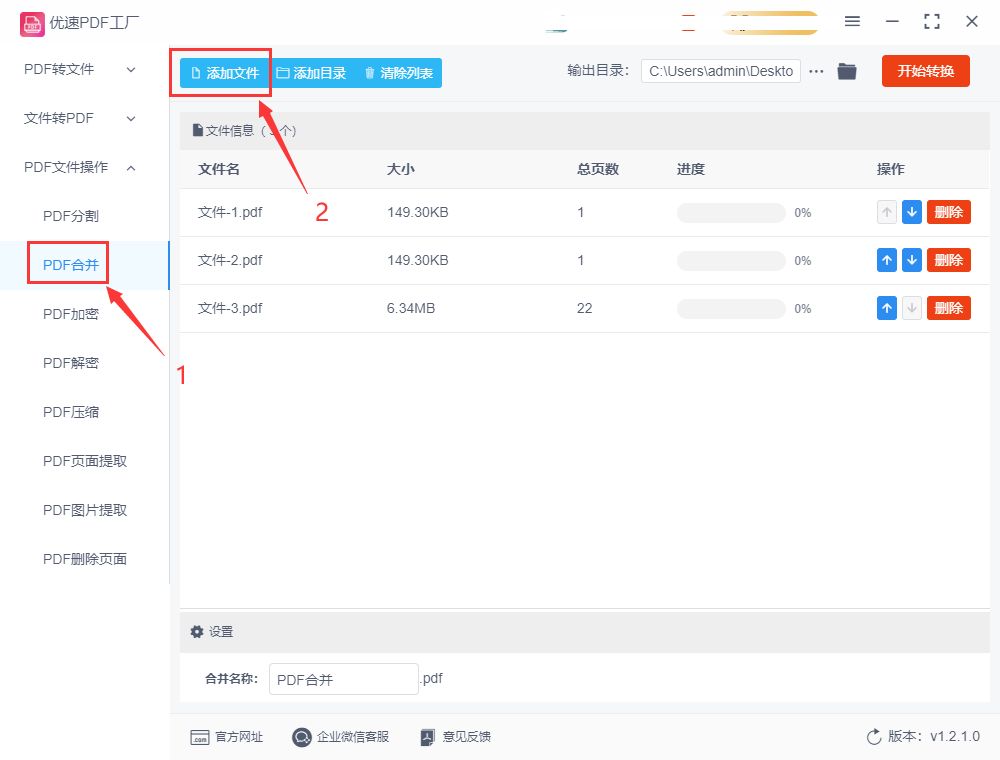
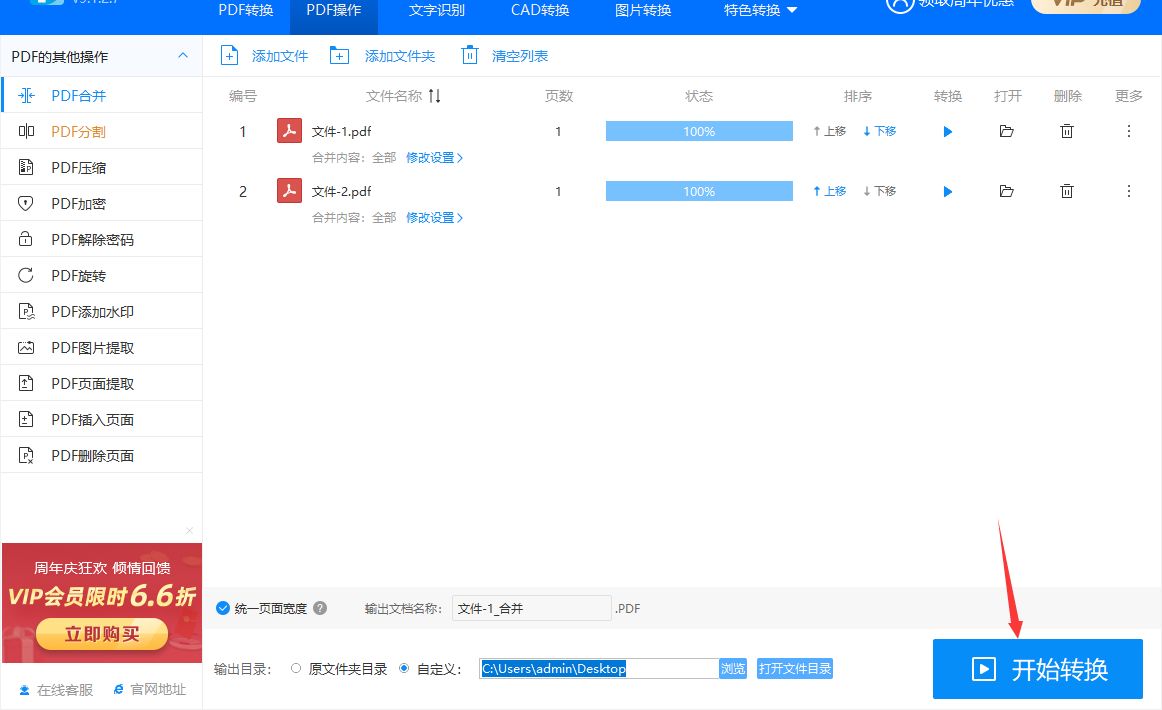
步骤4,如下图所示点击操作下面的箭头,就可以达到调整pdf文件上下顺序的目的,软件将以从上到下的方式进行文件合并。另外还可以对合并后的pdf文件名进行设置,如果不设置就采用默认名称。
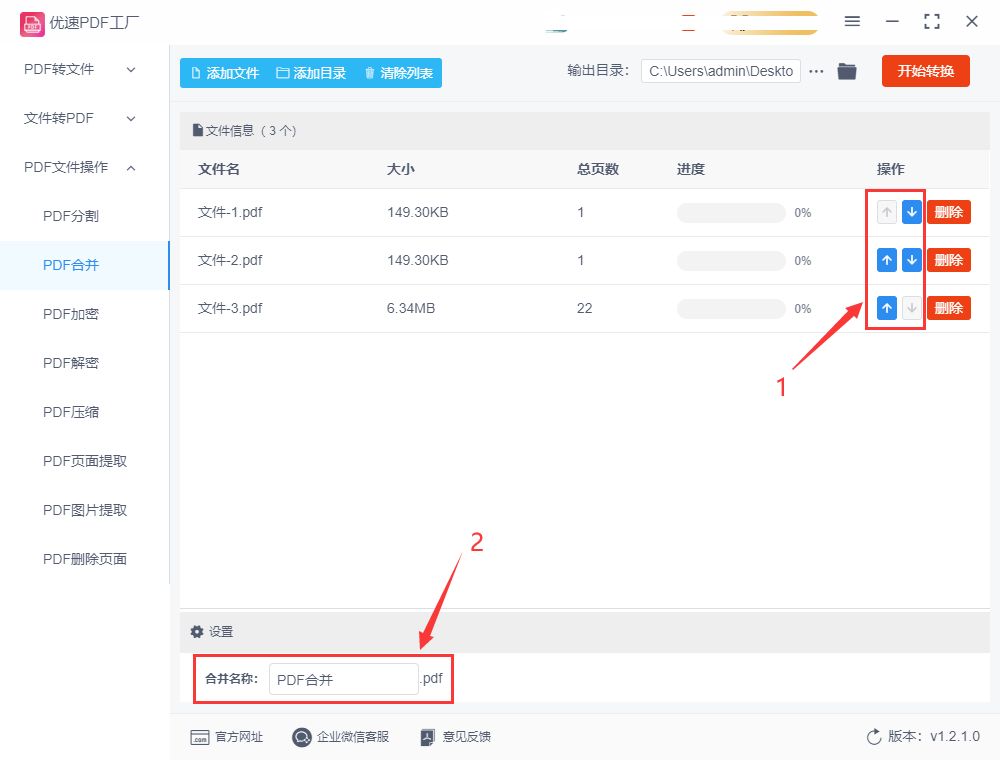
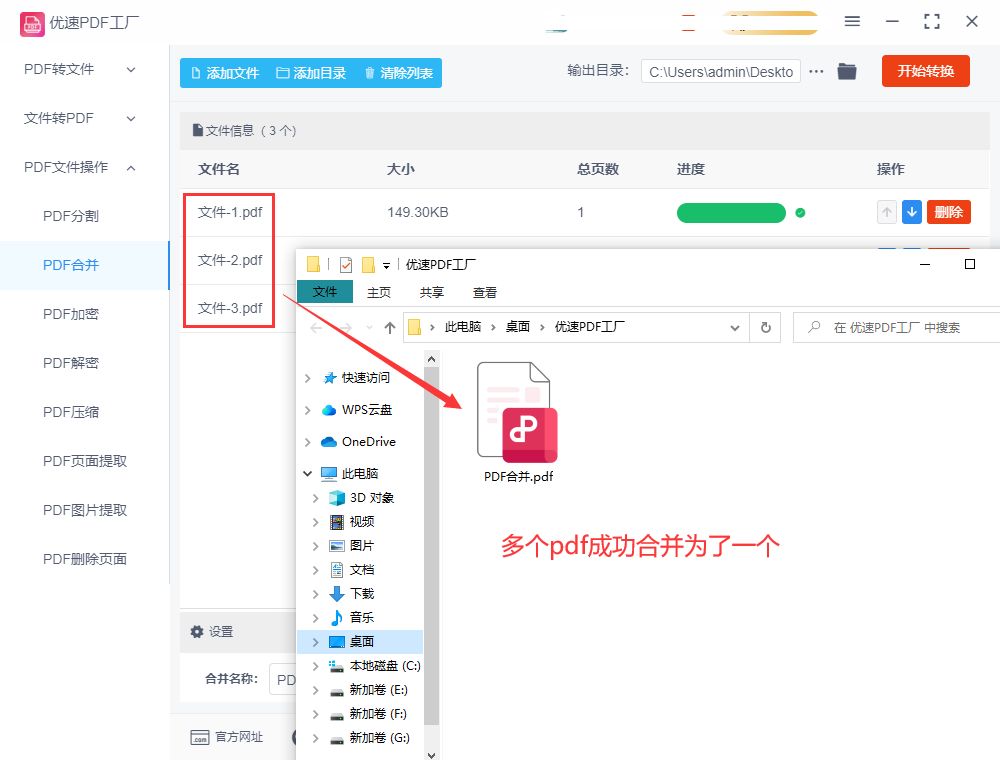
步骤5,所有准备工作都完成后,点击【开始转换】红色按钮就能够启动软件了,合并完成后软件会自动打开输出文件夹。合并需要花多少时间要根据pdf文件数量多少来决定,合并的文件越多时间就越久。
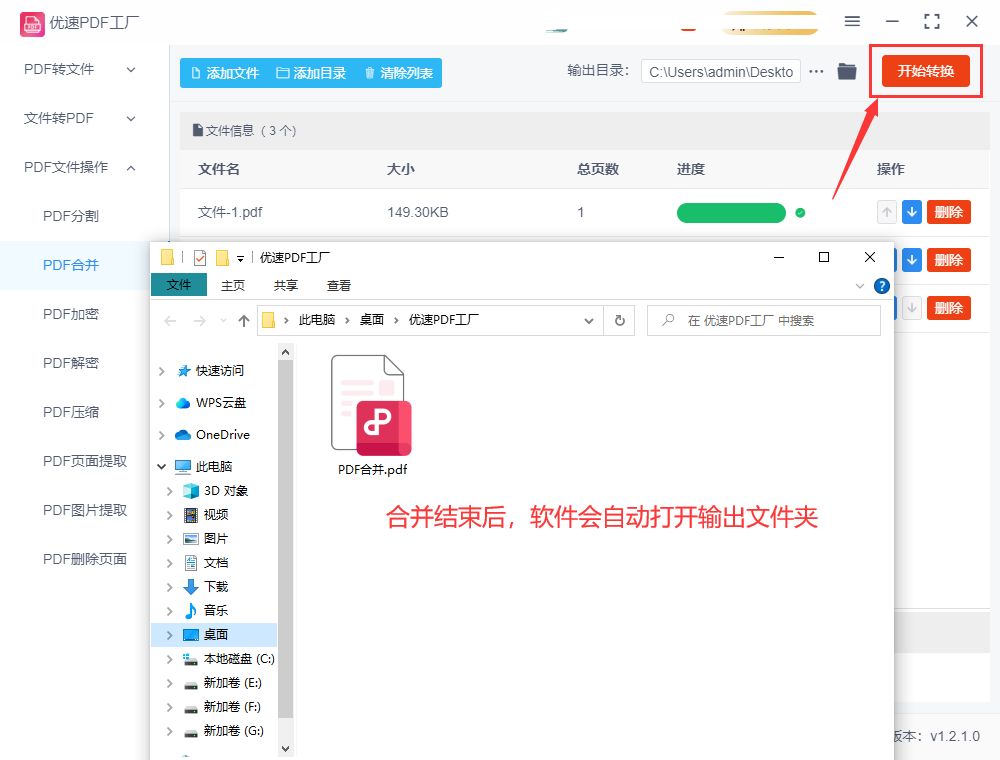
步骤6,从下面的结果图不难看出,软件成功地将上传的4个pdf文件合并为了一个,圆满的完成了本次合并任务。
pdf合并的方法二:使用Bigpdf在线工具进行合并
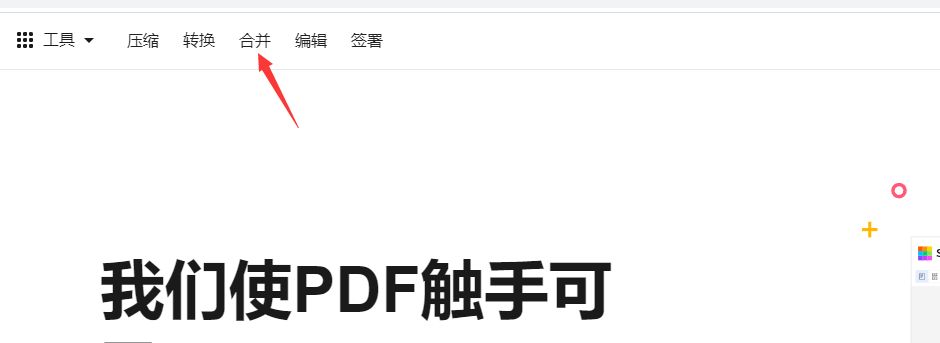
使用在线工具进行转换的时候不需要额外的安装软件,大家使用浏览器就可以将本次操作需要用到的bigpdf在线工具打开并使用,这是一个比较专业的pdf文件处理网站,在网站上我们就能看到“合并”功能选项,我们点击此功能直接进入内页。
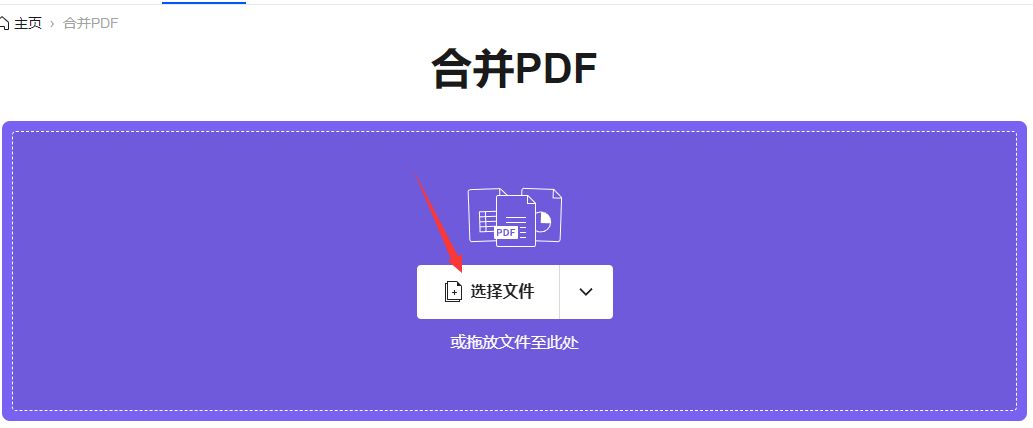
进入合并pdf文件的操作页面后,点击页面上紫色方框中的任意一个地方,就可以将等待合并的pdf文件进行上传,上传的pdf文件数量没有限制。
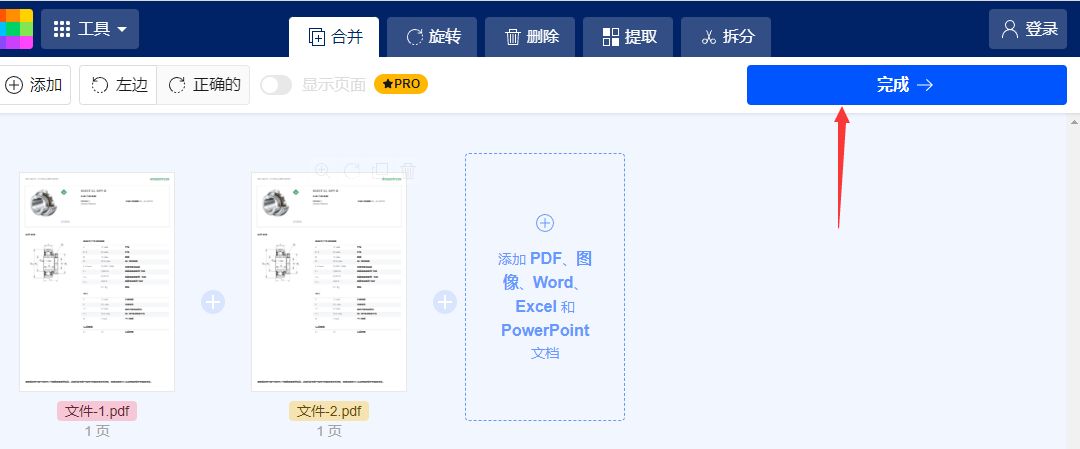
上传成功后可以看到文件缩略图,鼠标拖动文件缩略图可以起到调整文件顺序的作用。最后我们点击“完成→”蓝色按钮,正式开启合并程序。
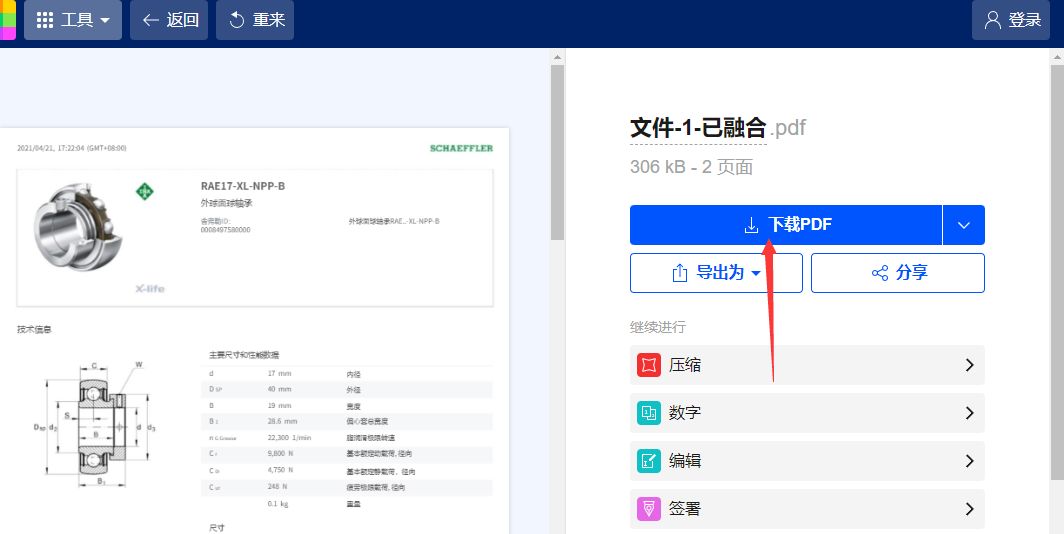
合并完成后软件的右侧会提示“已融合”的提示,然后点击下面的“下载PDF”蓝色按钮,就可以将合并后的pdf文件下载到电脑本地进行使用了。
pdf合并的方法三:使用讯飞PDF处理器进行合并
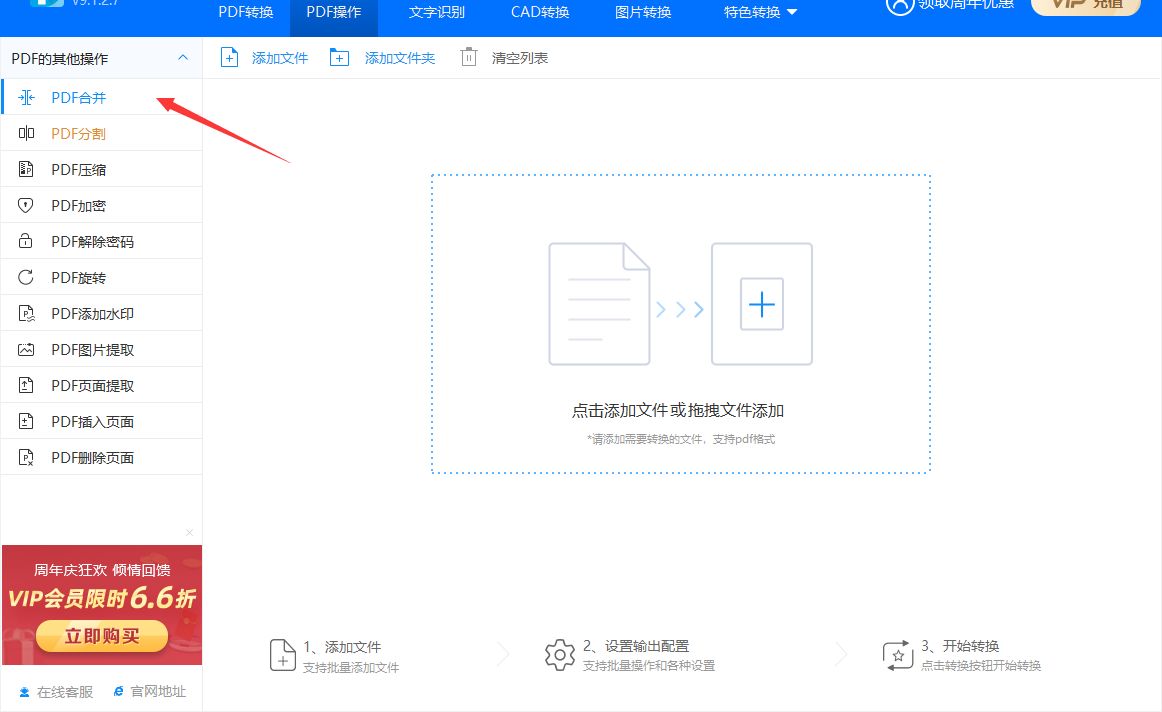
本方法进行合并之前请大家将用到的讯飞PDF处理器软件下载好,然后进行安装,打开软件之后,我们软件的上方可以看到六大选项,按照要求我们点击“PDF操作”,之后还需要在左侧的列表中点击“PDF合并”功能。
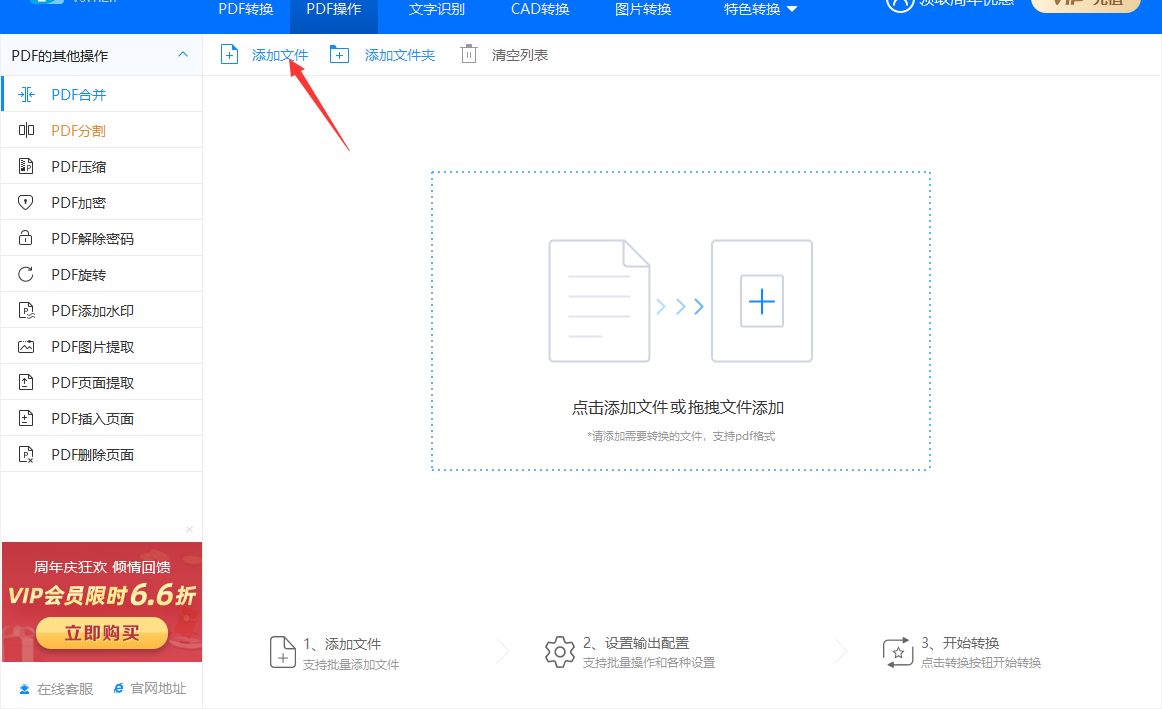
点击软件上的“添加文件”按钮,随后就可以上传需要合并的pdf文件到软件里面了,此外你还可以使用拖拽的方法进行文件的上传,拖拽添加文件似乎更方便一些。
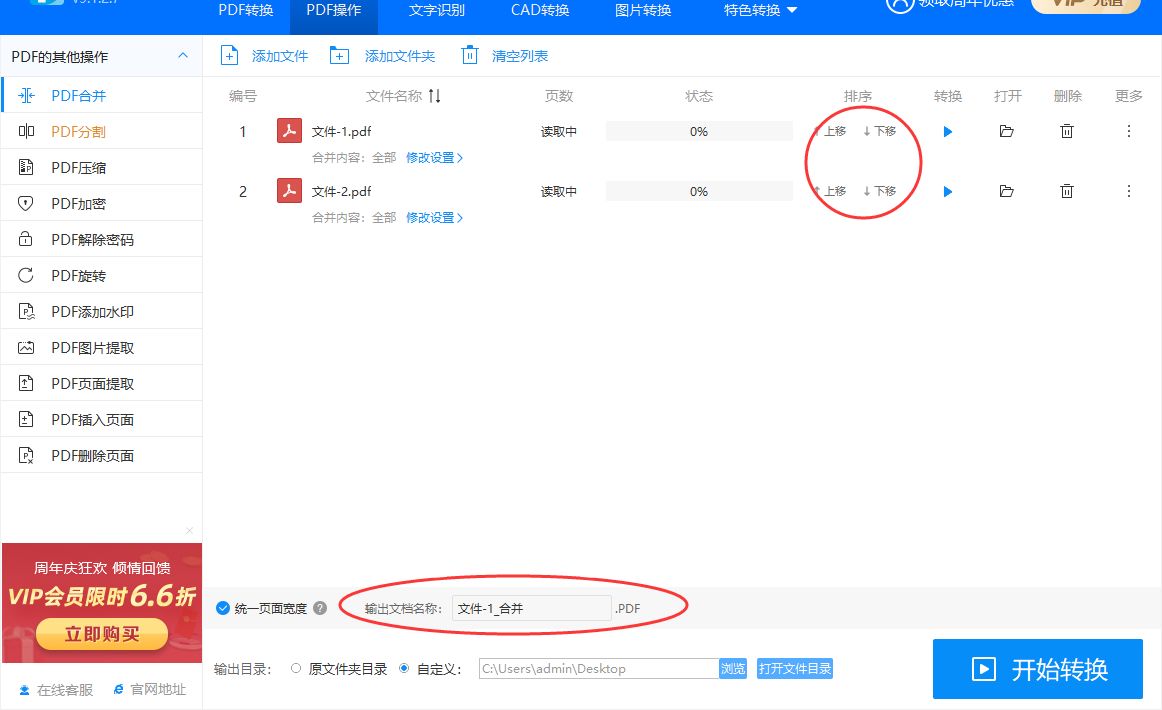
如下图所示,点击排序下面的上移或者下移文字按钮,就可以达到调整文件顺序的目的,合并顺序是从上到下进行的;此外你还可以在左下角设置合并后的文档名称,不设置的话就使用默认名称。
最后点击右下角的“开始转换”蓝色按钮后,就可以启动软件的合并程序了,文件越多合并所需的时间就越久,合并结束后可以看到进度条会变成100%,之后我们找到输出目录就能找到合并好的pdf文件了。
作为一名普通的职场人,平时面对最多的可能就是处理电脑文件了,文件处理能力的高低也是你工作能力高低的最好体现,快速完成领导教给的任务才能得到领导的赏识。pdf文件作为不可缺少的办公文件形式,我们一定也要学会关于它的一些处理小技巧,今天小编为大家介绍了几个关于“很多个pdf怎么合并在一起?”的电脑操作小技巧,相信大家看完后都会有收获,每天学习一点进步一点,记得点个赞再走哦。
相关文章:

很多个pdf怎么合并在一起?
很多个pdf怎么合并在一起?作为一个办公室的伙伴,对于PDF格式肯定不会陌生。它强大的功能为我们的工作提供了许多便利。由于PDF文件格式的稳定性和安全性较高,我们通常在工作或学习中使用它来传输文件,很多人都喜欢将办公文件都做成…...

Ubuntu apt更换国内镜像源,apt 更新源,apt 国内镜像
详细一篇: https://midoq.github.io/2022/05/30/Ubuntu20-04%E6%9B%B4%E6%8D%A2%E5%9B%BD%E5%86%85%E9%95%9C%E5%83%8F%E6%BA%90/ 更换方法 Ubuntu采用apt作为软件安装工具,其镜像源列表记录在/etc/apt/source.list文件中。 首先将source.list复制为s…...

时序预测 | MATLAB实现WOA-CNN-BiLSTM-Attention时间序列预测(SE注意力机制)
时序预测 | MATLAB实现WOA-CNN-BiLSTM-Attention时间序列预测(SE注意力机制) 目录 时序预测 | MATLAB实现WOA-CNN-BiLSTM-Attention时间序列预测(SE注意力机制)预测效果基本描述模型描述程序设计参考资料 预测效果 基本描述 1.MAT…...

VINS-Mono-后端优化 (一:预积分残差计算-IMU预积分约束)
这里先回顾一下预积分是怎么来的 VINS-Mono-IMU预积分 (三:为什么要预积分预积分推导) 这里贴出预积分的公式 具体含义解释看对对应的文章 整个误差函数如下 预积分 α \alpha α β \beta β γ \gamma γ 是用 IMU 预积分获得的增量&a…...
怎么调整excel表里面所有单元格中,某个相同字体大小,单元格中其他文字大小不变?
环境: excel 2021 python3.8 问题描述: 怎么调整excel表里面所有单元格里面1这个字体大小,单元格里面其他文字不变? excel表里面。很多单元格都有1,1和文字都是10号字体,现在想把全部1字字体调整为16号其他字大小都不变 解决方案: 一、使用python来实现,经过测…...

流式数据库引擎备受关注,亚信安慧AntDB数据库受邀参加“2023中国PostgreSQL数据库生态大会”
11月3日至5日,2023中国PostgreSQL数据库生态大会在北京中科院软件所大报告厅盛大召开,大会现场百余位专家学者、企业、用户代表及线上数千位观众,就近年来国产数据库技术与市场变革进行深入探讨。湖南亚信安慧科技有限公司(简称&a…...
)
kafka开启SSL认证(包括内置zookeeper开启SSL)
zookeeper和kafka的SSL开启都可单独进行 生成SSL证书 使用jre自带的keytool工具生成,linux和windows下生成的证书可以通用 生成含有一个私钥的keystore文件,有效期10年(本文证书密码统一使用test123) keytool -genkeypair -ali…...
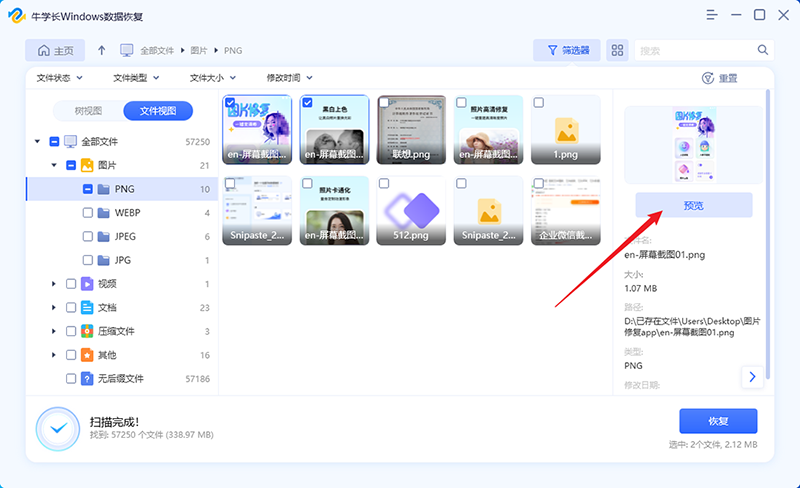
Powerpoint不小心被覆盖?PPT误删文件如何恢复?
PowerPoint不小心删除了,这可能是众多学生和工作人员最头痛的事情了。PPT被覆盖或误删可能意味着几个小时的努力付之东流。那么PPT覆盖的文档要如何救回来呢?小编将会在本篇文章中为大家分享几个解决方案,使PPT文档覆盖还原操作成为可能&…...

美团产品经理面试题大解密:流量VS口碑,如何找到最佳平衡点?
大家好,我是你们的小米。最近我参加了一场美团的产品经理面试,其中一个问题让我颇为犯愁:“产品应该追求高流量还是高口碑?”这个问题困扰了很多产品经理,因为两者似乎都对产品的成功有着重要影响。今天我就来和大家一…...
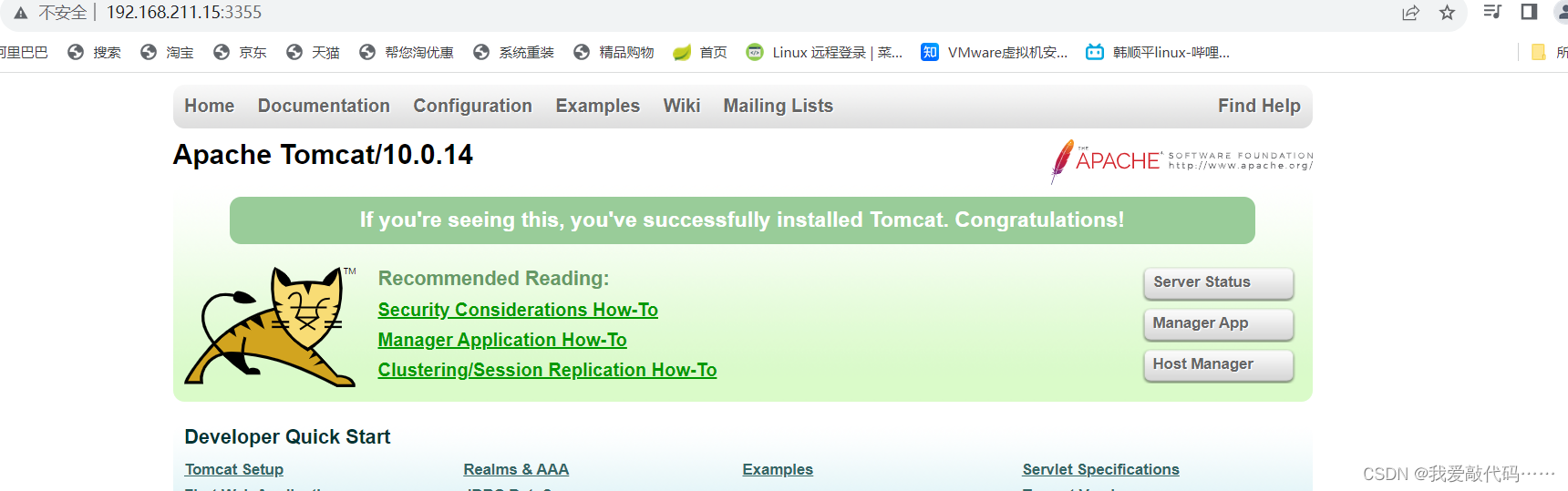
docker部署tomcat
1.下载tomcat镜像 尽量去下载最新版本 直接输入docker pull tomcat 后面不跟版本号(要是跟版本号,你还要去官网去查看是否有此版本,太麻烦了) 2.查看镜像 3.通过镜像去run启动容器 -d 就是后台运行 --name 给容器取个新名字 -p 3355:8080…...

大语言模型(LLM)综述(七):大语言模型设计应用与未来方向
A Survey of Large Language Models 前言8 A PRACTICAL GUIDEBOOK OF PROMPT DESIGN8.1 提示创建8.2 结果与分析 9 APPLICATIONS10 CONCLUSION AND FUTURE DIRECTIONS 前言 随着人工智能和机器学习领域的迅速发展,语言模型已经从简单的词袋模型(Bag-of-…...
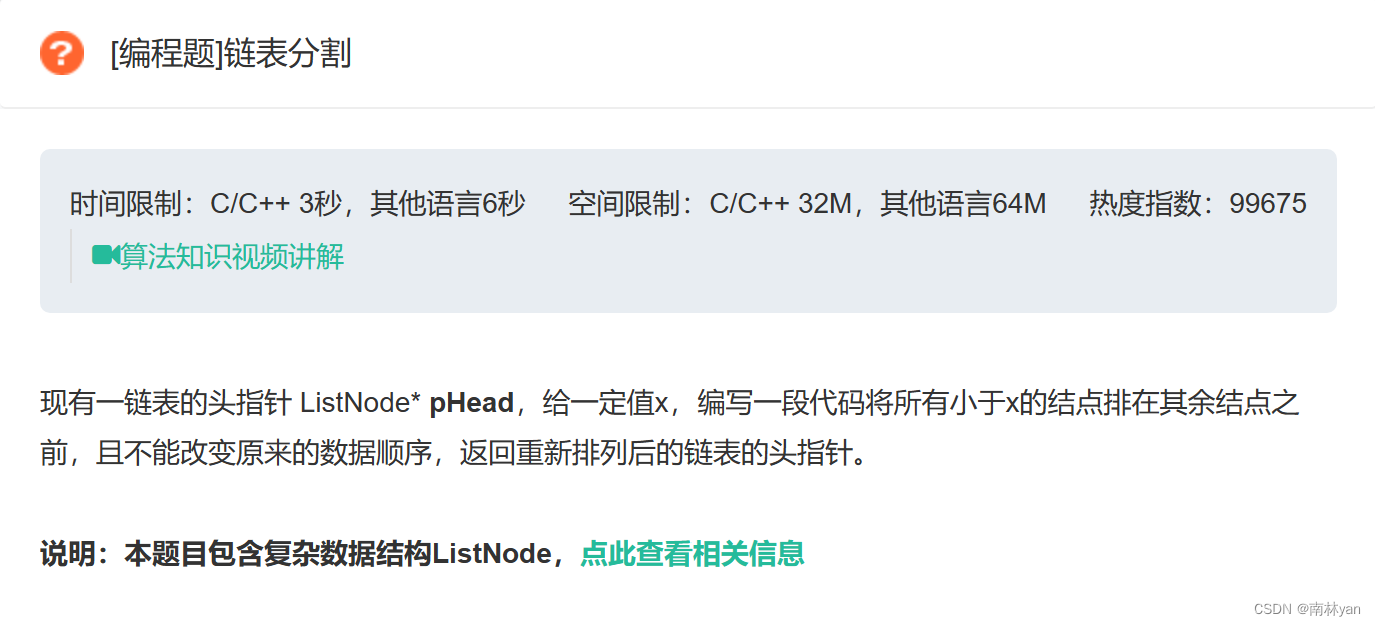
牛客网:链表分割
一、题目 函数原型: ListNode* partition(ListNode* pHead, int x) 二、思路 根据题意,可以设置两个新的链表,将原链表中所有小于x的结点链接到链表1中,大于x的结点链接到链表2中,最后再将两个链表合并即可。 此题有两…...
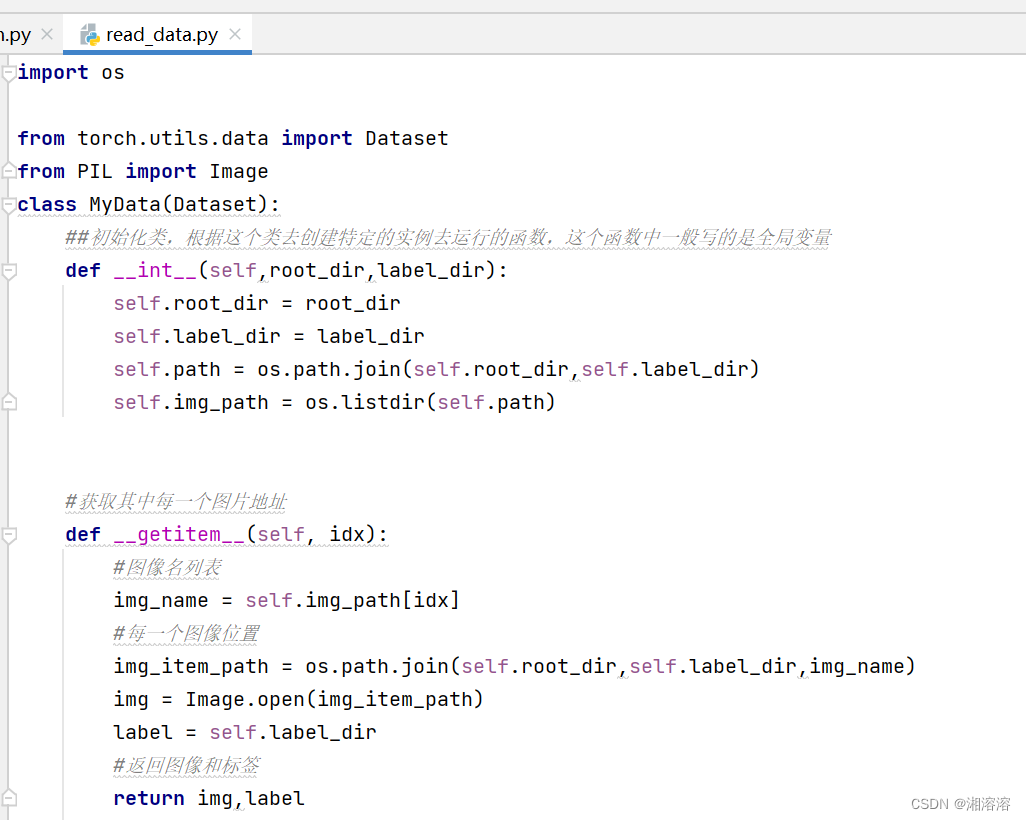
pytorch(小土堆)深度学习
第五节课讲项目的创建和对比 第六节:Dataset,Dataloader Dataset提供一种方式区获取数据及其label(如何获取每一个数据及其label,告诉我们总共有多少的数据) Dataloader为后面的网络提供不同的数据形式 第七节:Dataset类代码实战 显示图片 f…...

统计 boy girl 复制出来多少次。 浴谷 P1321题
统计 boy girl 复制出来多少次。 #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <iomanip>void fun(char* s) {int boy 0, girl 0;int t 0;while (*s) {if (t 0 && *s!.) {t 1;if (*s b || *s o || *s y)boy 1;elsegirl 1;}…...

odoo16前端框架分析1 boot.js
odoo16前端框架分析1 boot.js odoo16的前端基于owl组件系统,这是一个类似vue,react的现代js框架。 前端框架都放在了web模块中,具体的位置是addons/web/static/src 不过今天要说的不是owl,而是跟前端启动有关的几个重要文件 1、…...

酷开科技持续推动智能投影行业创新发展
近年来,投影仪逐渐成为年轻人追捧的家居时尚单品。据国际数据公司(IDC)报告显示,2022年中国投影机市场总出货量505万台,超80%为家用投影仪。相比于电视,投影仪外观小巧、屏幕大小可调节,无论是卧…...
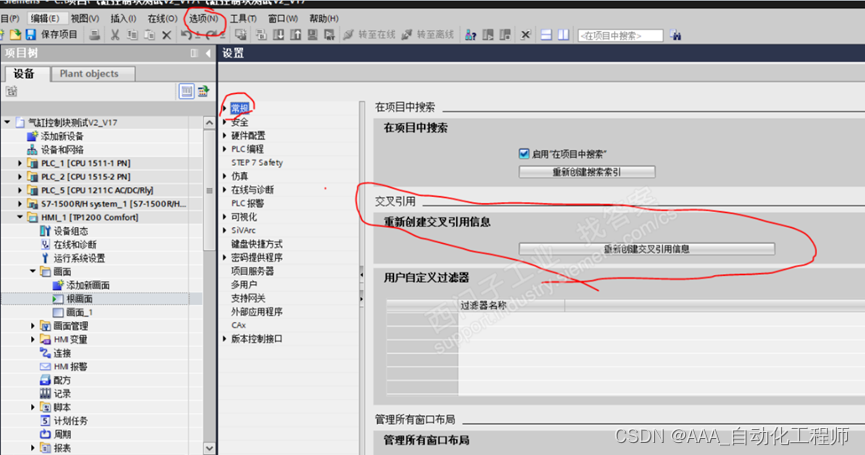
TIA博途中已经被调用的变量,为什么交叉引用时却没有显示调用信息?
TIA博途中已经被调用的变量,为什么交叉引用时却没有显示调用信息? 故障现象: 如下图所示,在HMI的画面中,已经连接了对应的变量, 如下图所示,这里为HMI变量表, 如下图所示ÿ…...
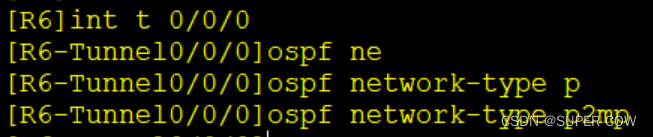
OSPF下的MGRE实验
一、实验要求 1、R1-R3-R4构建全连的MGRE环境 2、R1-R5-R6建立hub-spoke的MGRE环境,其中R1为中心 3、R1-R3...R6均存在环回网段模拟用户私网,使用OSPF使全网可达 4、其中R2为ISP路由器,仅配置IP地址 二、实验拓扑图 三、实验配置 1、给各路…...

论文速览 | TRS 2023: 使用合成微多普勒频谱进行城市鸟类和无人机分类
注1:本文系“最新论文速览”系列之一,致力于简洁清晰地介绍、解读最新的顶会/顶刊论文 论文速览 | TRS 2023: Urban Bird-Drone Classification with Synthetic Micro-Doppler Spectrograms 原始论文:D. White, M. Jahangir, C. J. Baker and M. Antoniou, “Urban Bird-Drone…...
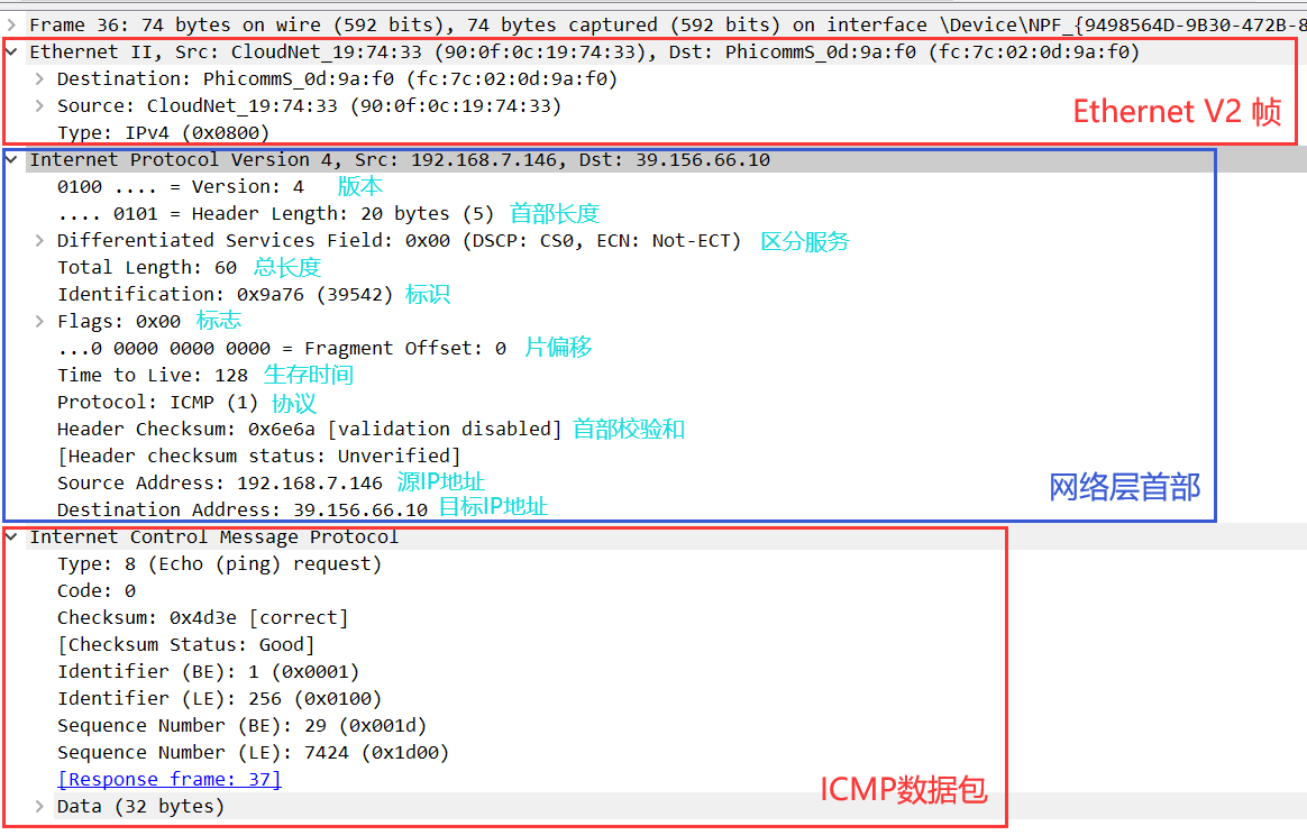
《网络协议》02. 物理层 · 数据链路层 · 网络层
title: 《网络协议》02. 物理层 数据链路层 网络层 date: 2022-08-31 22:26:48 updated: 2023-11-08 06:58:52 categories: 学习记录:网络协议 excerpt: 物理层(数据通信模型,信道)、数据链路层(封装成帧,…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
