数据结构与算法—插入排序选择排序
目录
一、排序的概念
二、插入排序
1、直接插入排序
直接插入排序的特性总结:
2、希尔排序
希尔排序的特性总结:
三、选择排序
1、直接选择排序
时间复杂度
2、堆排序—排升序(建大堆)
向下调整函数
堆排序函数
代码完整版:
头文件
函数文件
测试文件
一、排序的概念

二、插入排序
1、直接插入排序
直接插入排序是一种简单的排序算法,它的基本思想是将一个记录插入到已经排序好的有序表中,从而得到一个新的、记录数增加1的有序表。这个算法适用于少量数据的排序,是稳定的排序方法,即相等的元素的顺序不会改变。
直接插入排序的算法过程如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
如果我们将这个过程比作扑克牌的排序,每次我们都是从牌堆中拿出一张牌,然后将它插入到左手中正确的位置,最终左手中的牌都是排序好的。
我们来看一下代码的运行过程:
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) {int end = i;int tmp = a[i + 1];while (end >= 0) {if (a[end] > tmp) {a[end + 1] = a[end];end--;}else {break;}}a[end + 1] = tmp;}
}- 函数参数:指针a接收数组,n接收数组元素个数。
- 首先,外层循环从第一个元素开始遍历到倒数第二个元素,因为在内层循环中需要比较当前元素和前一个元素的大小,所以最后一个元素不需要再比较。
- 在外层循环中,我们将当前元素的下一个元素作为待插入元素,将当前元素的下标保存在变量end中,这个变量表示当前元素在已排序部分中的位置。
- 接下来while循环中,我们在已排序部分从后往前遍历,比较当前元素和已排序部分中的元素大小,如果当前元素小于已排序部分中的元素,则将已排序部分中的元素后移一位,直到找到当前元素的正确位置。
- 最后,我们将待插入元素插入到正确的位置,即end+1的位置。
- 内层循环结束后,当前元素已经被插入到了正确的位置,我们继续外层循环,处理下一个元素,直到所有元素都被插入到正确的位置。
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高2. 时间复杂度:O(N^2)3. 空间复杂度:O(1),它是一种稳定的排序算法4. 稳定性:稳定
2、希尔排序
希尔排序(Shell Sort)是一种改进的插入排序算法,它的基本思想是将待排序的序列分成若干个子序列,对每个子序列进行插入排序,然后再将整个序列进行一次插入排序。通过这种方式,可以使得序列中较小的元素尽可能地快速地移动到前面,从而减少了插入排序的比较次数和移动次数,提高了排序的效率。
希尔排序的算法过程如下:
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m的子序列,分别对每个子序列进行插入排序;
- 将各个子序列中的排序结果合并成一个序列。
代码如下:
void ShellSort(int* a, int n)
{//1、gap > 1 预排序//2、gap == 1 直接插入排序int gap = n;while (gap > 1) {gap = gap / 3 + 1;// +1可以保证最后一次一定是1for (int i = 0; i < n - gap; i++) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (a[end] > tmp) {a[end + gap] = a[end];end -= gap;}else {break;}}a[end + gap] = tmp;}}
}- 首先,我们选择一个增量gap=n,然后将序列分成若干个子序列,对每个子序列进行插入排序。
- 在这个实现中,我们使用了一个while循环来计算增量gap,每次将gap除以3并加1,保证gap最小为1,此时进行直接插入排序。
- 在外层while循环中,我们将序列分成若干个子序列,每个子序列的长度为gap。然后,我们对每个子序列进行插入排序,将子序列中的元素插入到已排序部分的正确位置。
-
在内层循环中,我们使用了一个变量end来表示当前元素的下标,每次将end减去gap,直到找到当前元素的正确位置。然后,我们将待插入元素插入到正确的位置,即end+gap的位置。
-
内层循环结束后,当前子序列已经排好序了,我们继续外层while循环,处理下一个子序列,直到所有子序列都被排好序了。
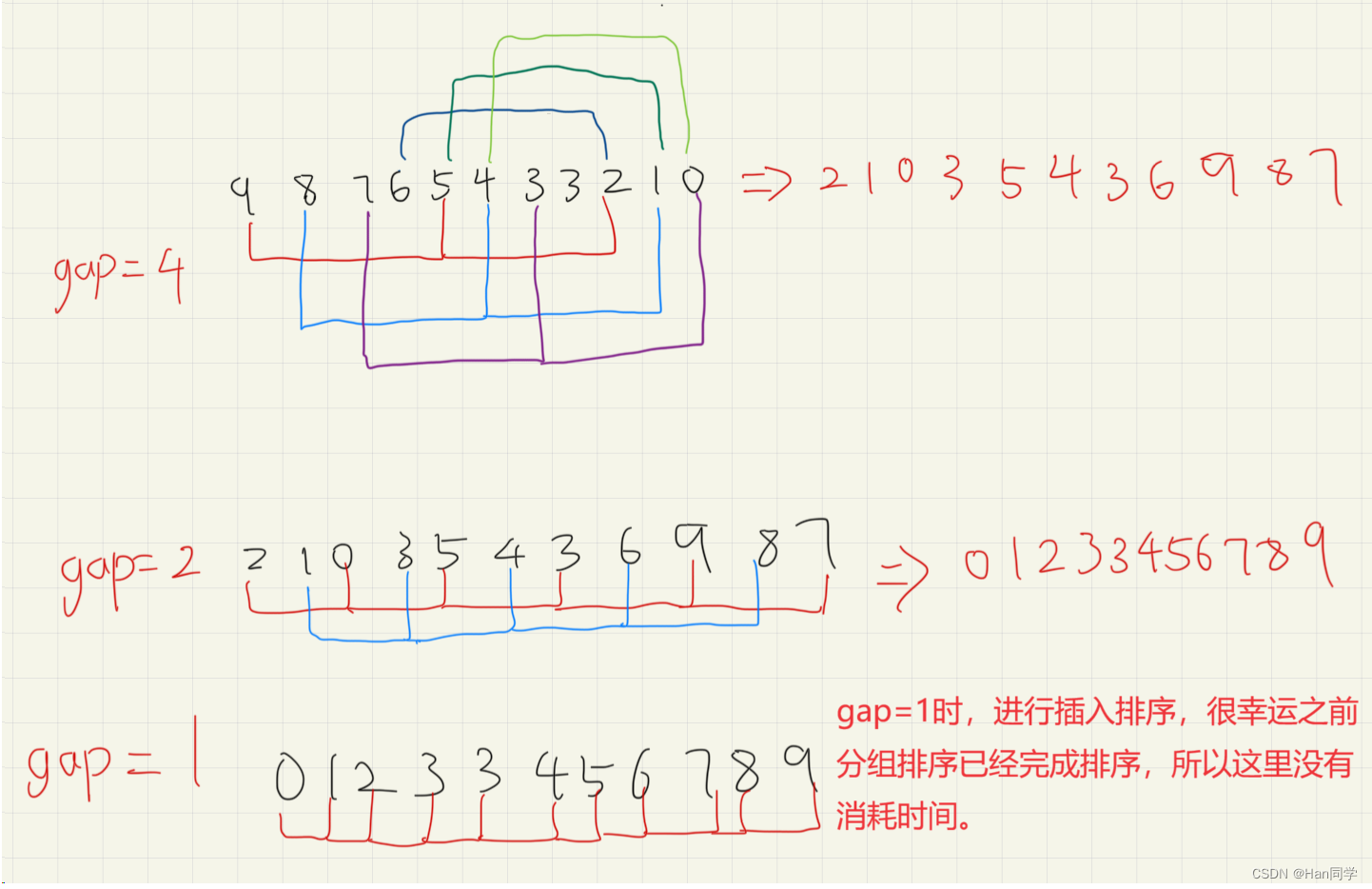
以数组 a = [9, 8, 7, 6, 5, 4, 3, 3, 2, 1, 0],长度 n = 11为例,演示排序过程
图中颜色相同的值为当前<间距gap>下的子序列,从前往后依次比较每个子序列(也就是相距 gap 个位置的值的大小)。
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间复杂度都不固定,但我们只需记住结论:O(N^ 1.3),复杂的推导和计算过程不需要了解。
三、选择排序
1、直接选择排序
直接选择排序通过每一轮的比较,找到最大值和最小值,将最大值的节点跟右边交换,最小值节点跟左边交换,达到排升序的效果。
我们先看代码,然后通过一个例子就能明白了。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int maxi = begin, mini = begin;for (int i = begin; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);// 如果maxi和begin重叠,修正一下即可if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}- 代码中的变量begin和end分别表示当前未排序的元素范围的起始和结束位置。
- 在while循环中,每次从begin到end的范围内找到最大和最小的元素,分别用maxi和mini记录它们的下标。
- 然后将mini所指向的元素与begin所指向的元素交换位置,将maxi所指向的元素与end所指向的元素交换位置。
- 如果maxi和begin重叠,说明mini所指向的元素是当前未排序元素中最大的,需要将maxi更新为mini。
- 最后,begin指针向后移动一位,end指针向前移动一位,继续进行下一轮排序。
我们来用一个简单的例子演示一下这个选择排序算法的过程。
假设我们有一个数组`a`,它的元素为:[5, 3, 8, 6, 4, 2],我们要对它进行排序。
首先,begin指向第一个元素,end指向最后一个元素:
begin = 0
end = 5接下来,我们进入主循环,因为`begin`小于`end`,所以我们需要继续排序。在第一轮排序中,我们需要找到未排序部分的最大值和最小值。
首先,我们将`maxi`和`mini`都初始化为`begin`,也就是第一个元素的索引。然后,我们遍历未排序部分的元素,找到最大值和最小值的索引。在这个例子中,最大值的索引是2,最小值的索引是5。
maxi = 2
mini = 5接下来,我们将未排序部分的最小值交换到开始位置,将未排序部分的最大值交换到结束位置。这时,数组的状态变为:[2, 3, 4, 6, 8, 5]
由于我们已经将当前范围的最大值和最小值放到了正确的位置,所以我们将`begin`向后移动一位,将`end`向前移动一位,继续进行下一轮排序。此时,`begin`指向第二个元素,`end`指向倒数第二个元素:
begin = 1
end = 4在第二轮排序中,我们需要找到未排序部分的最大值和最小值。这时,最大值的索引是3,最小值的索引是1。
maxi = 3
mini = 1接下来,我们将未排序部分的最小值交换到开始位置,将未排序部分的最大值交换到结束位置。这时,数组的状态变为:[2, 3, 4, 5, 6, 8],所有元素都排序完成,排序结束。
时间复杂度
每一轮比较都需要遍历数组,查找最大最小值,第一轮遍历N个数据,第二轮是N-2个数据,第三轮N-4 …,遍历次数为:N+N-2+N-4+…+1,一个等差数列求和,所以总的时间复杂度为O(N^2)
2、堆排序—排升序(建大堆)
向下调整函数
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child])++child;if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}- 通过传入参数获取到当前的左子节点的位置。
- 当child位置小于数组元素个数时进行判断。
- 进入循环,首先判断检查右子节点是否存在并且比左子节点的值大,如果是,将
child更新为右子节点的索引,以确保选择更小的子节点进行比较。 - 比较选定的子节点的值与父节点的值,如果子节点的值大于父节点的值,就交换它们。
- 更新parent为新的子节点位置,更新child为新的左子节点位置,然后继续比较和交换,直到不再需要交换为止。
- 如果当前子节点不大于当前父节点则停止循环。
堆排序函数
// 排升序
void HeapSort(int* a, int n)
{// 建大堆for (int i = (n-1-1)/2; i >= 0; --i){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}- 在HeapSort函数中,第一个循环调用了AdjustDown函数,将待排序数组构建成了一个大堆。但是,这个大堆并不是完全有序的,只是满足了大堆的性质,即每个节点的值都大于或等于其左右子节点的值。因此,需要进行第二个while循环,将大堆中的元素依次取出,交换堆顶元素和数组末尾元素,并重新调整大堆,直到整个数组有序。
- 第二个while循环中,将堆顶元素与数组末尾元素交换,然后将剩余元素重新调整为大堆。这样,每次交换后,数组末尾的元素就是当前大堆中的大值,而剩余元素仍然满足大堆的性质。重复以上步骤,直到整个数组有序。
代码完整版:
头文件
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>void PrintArray(int* a, int n);
void InsertSort(int* a, int n);
void ShellSort(int* a, int n);
void SelectSort(int* a, int n);
void HeapSort(int* a, int n);函数文件
#include "sort.h"void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++) {printf("%d ", a[i]);}printf("\n");
}void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) {int end = i;int tmp = a[i + 1];while (end >= 0) {if (a[end] > tmp) {a[end + 1] = a[end];end--;}else {break;}}a[end + 1] = tmp;}
}void ShellSort(int* a, int n)
{//1、gap > 1 预排序//2、gap == 1 直接插入排序int gap = n;while (gap > 1) {gap = gap / 3 + 1;// +1可以保证最后一次一定是1for (int i = 0; i < n - gap; i++) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (a[end] > tmp) {a[end + gap] = a[end];end -= gap;}else {break;}}a[end + gap] = tmp;}}
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int maxi = begin, mini = begin;for (int i = begin; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);// 如果maxi和begin重叠,修正一下即可if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child + 1] > a[child]) {child++;}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; --i) {AdjustDown(a, n, i);}int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
测试文件
#include"Sort.h"
#include<time.h>void TestInsertSort()
{//int a[] = { 4,7,1,9,3,4,5,8,3,2 };int a[] = { 4,7,1,9,3,6,5,8,3,2,0 };PrintArray(a, sizeof(a) / sizeof(int));InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestSelectSort()
{//int a[] = { 4,7,1,9,3,6,5,8,3,2,0 };int a[] = { 9,7,1,3,3,0,5,8,3,2,3 };PrintArray(a, sizeof(a) / sizeof(int));SelectSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestHeapSort()
{int a[] = { 4,7,1,9,3,6,5,8,3,2,0 };PrintArray(a, sizeof(a) / sizeof(int));HeapSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestOP()
{srand(time(0));const int N = 1000000;//运行时间较长可自行更改大小int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelcetSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{//TestInsertSort();//TestShellSort();//TestSelectSort();//TestHeapSort();TestOP();return 0;
}相关文章:

数据结构与算法—插入排序选择排序
目录 一、排序的概念 二、插入排序 1、直接插入排序 直接插入排序的特性总结: 2、希尔排序 希尔排序的特性总结: 三、选择排序 1、直接选择排序 时间复杂度 2、堆排序—排升序(建大堆) 向下调整函数 堆排序函数 代码完整版: …...

基于词云图的短信热词数据可视化
热词统计:短信、邮件、微信、QQ、微博、电商评价、新闻、各行业热词(旅游、世界杯、战争、考研等)、热点事件等场景。 展示模型:给定多段文本,绘制出词云图。 核心思想:根据样本集中的文本包含的高频词…...
Linux/centos上如何配置管理Web服务器?
Linux/centos上如何配置管理Web服务器? 1 Web简单了解2 关于Apache3 如何安装Apache服务器?3.1 Apache服务安装3.2 httpd服务的基本操作 4 如何配置Apache服务器?4.1 关于httpd.conf配置4.2 常用指令 5 简单实例 1 Web简单了解 Web服务器称为…...
Java EE进阶2
包如果下载不下来怎么办? 1,确认包是否存在 2.如果包存在就多下载几次 3.如果下载了很多次都下载不下来,看看是不是下面几步出现了问题? 1)是否配置了国内源 settings.xml 2)目录是否为全英文,存在中文的话就修改路径 3)删除本地仓库的 jar 包,重新下载(可能由于网络的原…...

最新AI系统ChatGPT源码+AI绘画系统源码+支持GPT4.0+Midjourney绘画+搭建部署教程+附源码
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...

大厂面试题-为什么一线互联网公司严禁使用存储过程
之所以互联网公司不让用,主要有几个方面的原因: 1.存储过程不好调试,一旦涉及到非常复杂的逻辑,定位问题的时候比较麻烦 2.存储过程的一致性很差,如果从Oracle迁移到MySQL,涉及到部分数据库独有特性的时候…...

SpringBoot+Swagger详细使用方法
一、接口文档概述 swagger是当下比较流行的实时接口文文档生成工具。接口文档是当前前后端分离项目中必不可少的工具,在前后端开发之前,后端要先出接口文档,前端根据接口文档来进行项目的开发,双方开发结束后在进行联调测试。 二…...
[动态规划] (十二) 简单多状态 LeetCode 213.打家劫舍II
[动态规划] (十二) 简单多状态: LeetCode 213.打家劫舍II 文章目录 [动态规划] (十二) 简单多状态: LeetCode 213.打家劫舍II题目解析解题思路状态表示状态转移方程初始化和填表顺序返回值提醒 代码实现总结 213. 打家劫舍 II 题目解析 本题是对打家劫舍和按摩师的升级题型&am…...

算法与数据结构之链表
链表的定义,相信大家都知道,这里就不赘述了只是链表分单向链表和双向链表,废话不多说,直接上代码 链表节点的定义: public class Node {int val;Node next;Node pre;public Node(int val, Node next, Node pre) {thi…...

深入剖析React Hooks中的 useCallback
前言 自 React 16.8 版本引入 Hooks 以来,useCallback 成为了前端开发者们越来越青睐的一个功能。useCallback 可以有效优化组件性能,尤其在处理函数式组件中的状态更新时。本文将详细介绍 useCallback 的用法及其注意事项。 1. useCallback 简介 use…...

微服务中配置文件(YAML文件)和项目依赖(POM文件)的区别与联系
实际上涉及到了微服务架构中的两个重要概念:服务间通信和项目依赖管理。在微服务架构中,一个项目可以通过两种方式与另一个项目建立依赖关系:通过配置文件(如YAML文件)和通过项目依赖(如POM文件)…...
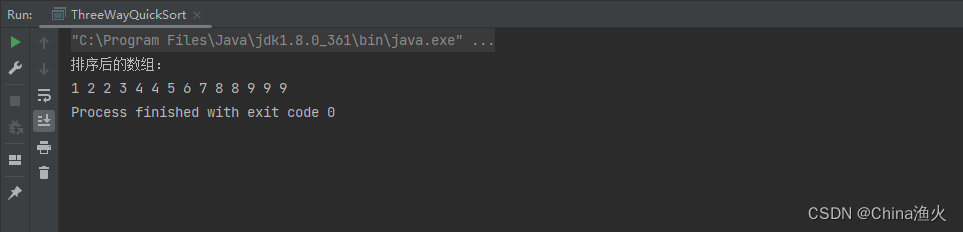
Java快速排序算法、三路快排(Java算法和数据结构总结笔记)[7/20]
一、什么是快速排序算法 快速排序的基本思想是选择一个基准元素(通常选择最后一个元素)将数组分割为两部分,一部分小于基准元素,一部分大于基准元素。 然后递归地对两部分进行排序,直到整个数组有序。这个过程通过 par…...

【React】05.JSX语法使用上的细节
水水水水水...

LeetCode 1759. 统计同质子字符串的数目【字符串】1490
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
IDDR)
FPGA UDP RGMII 千兆以太网(2)IDDR
1 xilinx原语 在 7 系列 FPGA 中实现 RGMII 接口需要借助 5 种原语,分别是:IDDR、ODDR、IDELAYE2、ODELAYE2(A7 中没有)、IDELAYCTRL。其中,IDDR和ODDR分别是输入和输出的双边沿寄存器,位于IOB中。IDELAYE2和ODELAYE2,分别用于控制 IO 口输入和输出延时。同时,IDELAYE2 …...

chrome安装vue devtools
不能访问应用商店 如果可以访问应用商店可以往下看 插件源代码 选择shell-chrome,这是官方的插件源码 下载源代码打包 参考教程 点击扩展按钮->管理扩展程序->打开开发者模式->把crx文件拖拽进去即可 可以访问chrome应用商店 插件地址 官方文档地址 选…...
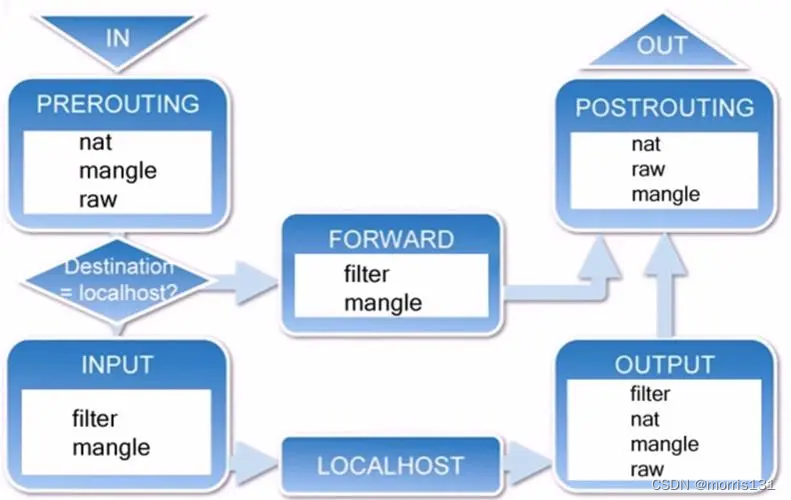
【Docker】iptables命令的使用
iptables是一个非常强大的Linux防火墙工具,你可以使用它来控制网络流量的访问和转发。 前面已经学习了iptables的基本原理,四表五链的基本概念,也已经安装好了iptables,下面我们主要学习iptables命令的基本使用。 可以使用iptable…...

Flex bison 学习好代码
计算机的重要课程编译原理很难学吧, 但是要会用flex &bison的话,容易理解一些。 有些好的项目可以帮助我们,比如 https://github.com/jgarzik/sqlfun 可以帮我们,下载 下来。 在cygwin 下面或者linux 运行: …...
学习Nginx配置
1.下载地址 官网地址:NGINX - 免费试用、软件下载、产品定价 (nginx-cn.net) 我这边选择NGINX 开源版 nginx: download 2.nginx的基本配置 配置文件语法 配置文件组成:注释行,指令块配置项和一系列指令配置项组成。 单个指令组成&#x…...
怎么批量获取文件名,并保存到excel?
怎么批量获取文件名?什么叫批量获取文件名,其实也非常好理解,就是面对大量文件是可以一次性的获取所有文件名称,这项技术的应用也是非常常见的,为什么这么说呢?现在很多的文档管理人员或者公司的文员&#…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
