【目标检测】SSD损失函数详解
文章目录
- 定位损失 L l o c L_{loc} Lloc
- 偏移值的计算
- smooth L1 loss
- 置信率损失 L c o n f L_{conf} Lconf
最近看看这个古早的目标检测网络,看了好多文章,感觉对损失函数的部分讲得都是不很清楚得样子,所以自己捋一下。
首先,SSD 得损失函数由两部分得加权和,一部分是定位损失 L l o c L_{loc} Lloc,另一部分是分类置信率损失 L c o n f L_{conf} Lconf。公式一般写成: L ( x , c , l , g ) = 1 N ( L c o n f ( x , c ) + α L l o c ( x , l , g ) ) L(x,c,l,g) = \frac{1}{N}\left( L_{conf}(x, c) + \alpha L_{loc}(x, l, g) \right) L(x,c,l,g)=N1(Lconf(x,c)+αLloc(x,l,g))总结来说,定位损失 L l o c L_{loc} Lloc 是使用 smooth L1 loss 来计算的,而分类置信率损失 L c o n f L_{conf} Lconf 是通过 softmax loss 来计算的。
定位损失 L l o c L_{loc} Lloc
接下来就分开讲讲两部分,首先是定位损失 L l o c L_{loc} Lloc, 它的公式可以写成: L l o c ( x , l , g ) = ∑ i ∈ P o s N ∑ m ∈ { c x , c y , w , h } x i j p ⋅ s m o o t h L 1 ( l i m − g ^ j m ) L_{loc}(x, l, g) = \sum_{i \in Pos}^{N} \sum_{m \in \left\{ cx, cy, w, h \right\}} x_{ij}^p \cdot \mathbf{smooth_{L1}}(l_i^m - \hat{g}_j^m) Lloc(x,l,g)=i∈Pos∑Nm∈{cx,cy,w,h}∑xijp⋅smoothL1(lim−g^jm)下昂西介绍一下里面的各种参数的含义:
- i ∈ P o s i \in Pos i∈Pos:第一个求和下的 P o s Pos Pos 是一个集合,我们知道在训练的时候,会根据 IOU(SSD 里好像是大于 0.5) 对 Default box(其实和 anchor 的含义一样)与 Ground truth box(后面统称 gt box)进行匹配,如果 第 i i i 个 default box 与 第 j j j 个 gt box 匹配上了,那么这个 default box i i i 就会被放入 P o s Pos Pos 的集合中,表示 positive,也就是被标记成了正样本。
- N N N:是正样本集合 P o s Pos Pos 的总数,表示有 N N N 个 default box 与 gt box 匹配上了。
- m ∈ { c x , c y , w , h } m \in \left\{ cx, cy, w, h \right\} m∈{cx,cy,w,h}:这四个值是 anchor 的位置参数,表示中心点的坐标和 anchor 的尺寸。
- x i j p x_{ij}^p xijp:可以理解为唯一标识 flag,如果 default box i i i 与 gt box j j j 是匹配的,gt box 的类别是 p p p,则为1,否则 0。
- l i m l_i^m lim:是预测值,也就是 bounding box 与 default box 的偏移值,不是真实的坐标,具体的转换在下面给出。
- g ^ j m \hat{g}_j^m g^jm:是真实值,是 gt box 与 default box 的偏移值。
偏移值的计算
回到前面提到的偏移值,如果 default box i i i 的位置参数是 { d i c x , d i c y , d i w , d i h } \{ d_i^{cx}, d_i^{cy}, d_i^{w}, d_i^{h} \} {dicx,dicy,diw,dih},gt box j j j 的位置参数是 { g j c x , g j c y , g j w , g j h } \{ g_j^{cx}, g_j^{cy}, g_j^{w}, g_j^{h} \} {gjcx,gjcy,gjw,gjh},我们就可以算出真实值对应的偏移量 { g ^ j c x , g ^ j c y , g ^ j w , g ^ j h } \{ \hat{g}_j^{cx}, \hat{g}_j^{cy}, \hat{g}_j^{w}, \hat{g}_j^{h} \} {g^jcx,g^jcy,g^jw,g^jh}:
g ^ j c x = ( g j c x − d i c x ) d i w g ^ j w = log ( g j w d i w ) g ^ j c y = ( g j c y − d i c y ) d i h g ^ j h = log ( g j h d i h ) \begin{align*} \hat{g}_j^{cx} = \frac{(g_j^{cx} - d_i^{cx})}{d_i^w} & \space\space\space\space\space\space\space\space\space \hat{g}_j^{w} = \log\left( \frac{g_j^w}{d_i^w} \right)\\ \hat{g}_j^{cy} =\frac{ (g_j^{cy} - d_i^{cy})}{d_i^h} & \space\space\space\space\space\space\space\space\space \hat{g}_j^{h} = \log\left( \frac{g_j^h}{d_i^h} \right) \end{align*} g^jcx=diw(gjcx−dicx)g^jcy=dih(gjcy−dicy) g^jw=log(diwgjw) g^jh=log(dihgjh)同理,我们也可以通过预测得到的 bounding box 参数 { b i c x , b i c y , b i w , b i h } \{b_i^{cx}, b_i^{cy}, b_i^{w}, b_i^{h} \} {bicx,bicy,biw,bih} ,来计算得到 bounding box 的偏移量,也就是预测值 l l l。 l i c x = ( b i c x − d i c x ) d i w l i w = log ( b i w d i w ) l i c y = ( b i c y − d i c y ) d i h l i h = log ( b i h d i h ) \begin{align*} l_i^{cx} = \frac{(b_i^{cx} - d_i^{cx})}{d_i^w} & \space\space\space\space\space\space\space\space\space l_i^{w} = \log\left( \frac{b_i^w}{d_i^w} \right)\\ l_i^{cy} =\frac{ (b_i^{cy} - d_i^{cy})}{d_i^h} & \space\space\space\space\space\space\space\space\space l_i^{h} = \log\left( \frac{b_i^h}{d_i^h} \right) \end{align*} licx=diw(bicx−dicx)licy=dih(bicy−dicy) liw=log(diwbiw) lih=log(dihbih)
中心点的偏移量计算是很好理解的,为什么宽高的偏移量要用 log 函数来算呢?
smooth L1 loss
SSD 是用到 smooth L1 loss 来计算真实值与预测值之间的差异: s m o o t h L 1 ( x ) = { 0.5 x 2 if ∣ x ∣ < 1 ∣ x ∣ − 0.5 otherwise \mathbf{smooth_{L1}}(x) =\begin{cases} 0.5x^2 & \text{ if } |x|< 1 \\ |x| -0.5 & \text{ otherwise } \end{cases} smoothL1(x)={0.5x2∣x∣−0.5 if ∣x∣<1 otherwise
这篇文章我觉得解释得挺清晰的,比较了 L1 loss, L2 loss 和 smooth L1 loss 三者之间的优劣。也提到了 loc loss 的演进。
bounding box 回归损失函数,也就是用于定位边界框的损失函数,其演进线路如下:
我记得 YOLOv1 的损失函数,在计算位置损失的时候,还是使用的欧式距离,也就是所谓的 L2 loss。
L1 loss 是求两个数之间的绝对值距离,导数是常数(小于 0 则为 -1,大于等于 0 则为 1),在零点处是不平滑的;
L2 loss 是两个数之间差的平方,导数是 2 x 2x 2x(也可以看出,受到 x x x 的影响很大),但是在零点处是平滑的。多个 L2 loss 求和再平均也叫做 MSE loss (Mean Square Error)。
而我们的主角 smooth L1 loss,如名字所见,是平滑版的 L1 loss,导数为: d s m o o t h L 1 ( x ) d x = { x if ∣ x ∣ < 1 ± 1 otherwise \frac{ \mathrm{d} \space \mathbf{smooth_{L1}}(x)}{\mathrm{d}x} =\begin{cases} x & \text{ if } |x|< 1 \\ \pm1 & \text{ otherwise } \end{cases} dxd smoothL1(x)={x±1 if ∣x∣<1 otherwise 在零点附近都是平滑的,而且在其它区间都是常数,也不会出现 L2 loss 随着 x x x 的增大而在损失函数中占据主导地位。
置信率损失 L c o n f L_{conf} Lconf
下面就讲一下分类的置信率损失 L c o n f L_{conf} Lconf,完整的公式如下: L c o n f ( x , c ) = − ∑ i ∈ P o s N x i j p log c ^ i p − ∑ i ∈ N e g log c ^ i 0 where c ^ i p = exp ( c i p ) ∑ p exp ( c i p ) L_{conf}(x, c) = - \sum_{i \in Pos}^N x_{ij}^p\log{\hat{c}_i^p} - \sum_{i\in Neg} \log{\hat{c}_i^0} \space\space\space\space \text{where} \space\space\space\space \hat{c}_i^p=\frac{\exp{(c_i^p)}}{\sum_p \exp{(c_i^p)}} Lconf(x,c)=−i∈Pos∑Nxijplogc^ip−i∈Neg∑logc^i0 where c^ip=∑pexp(cip)exp(cip),从公式的形态,可以看出来是二元交叉熵。没错,其实 softmax loss 就相当于交叉熵和 softmax 的组合,先看看最后的 softmax 公式: c ^ i p = exp ( c i p ) ∑ p exp ( c i p ) \hat{c}_i^p=\frac{\exp{(c_i^p)}}{\sum_p \exp{(c_i^p)}} c^ip=∑pexp(cip)exp(cip)
- c i p c_i^p cip: 对于分类的部分,一般网络的全连接层会输出 P P P 个类别的向量,在 SSD 因为要考虑背景(背景是分类 0),这个长度为 P + 1 P+1 P+1 的向量经过 softmax 之后,所有值的和会被限制为 1。其中置信率最大的值即是 c i p c_i^p cip(目前这个值还没经过归一化),这表示 anchor i i i 是的类别是 p p p 的可能性最大。
- c ^ i p \hat{c}_i^p c^ip:是通过对 c i p c_i^p cip 进行 softmax 而得到的,表示 anchor i i i 是分类 p p p 的概率,值是位于 0~1 之间的。
然后就是主公式的各个参数的具体含义:
- x i j p x_{ij}^p xijp:含义同上面位置损失提到的,如果 anchor i i i 与 gt box j j j 是匹配的,gt box 的类别是 p p p,则为1,否则 0。
- c ^ i 0 \hat{c}_i^0 c^i0:就是背景的分类概率(负样本)。
其实这个公式也没什么难理解的。
大致就是这么多了,如果大家有什么不清楚的地方或者是文章哪里写错了,欢迎评论留言。
相关文章:

【目标检测】SSD损失函数详解
文章目录 定位损失 L l o c L_{loc} Lloc偏移值的计算smooth L1 loss 置信率损失 L c o n f L_{conf} Lconf 最近看看这个古早的目标检测网络,看了好多文章,感觉对损失函数的部分讲得都是不很清楚得样子,所以自己捋一下。 首先&#x…...
C【整数正序分解】
// 整数正序分解 #include <stdio.h> #include <stdlib.h>int main() {int x;scanf("%d", &x);// 13425/10000->1(int一个d)// 13425%10000->3425(这是x)// 10000/10-.1000(这是mask)int mask 1;int t x;while (t > 9){t / 10;mask * 10;…...
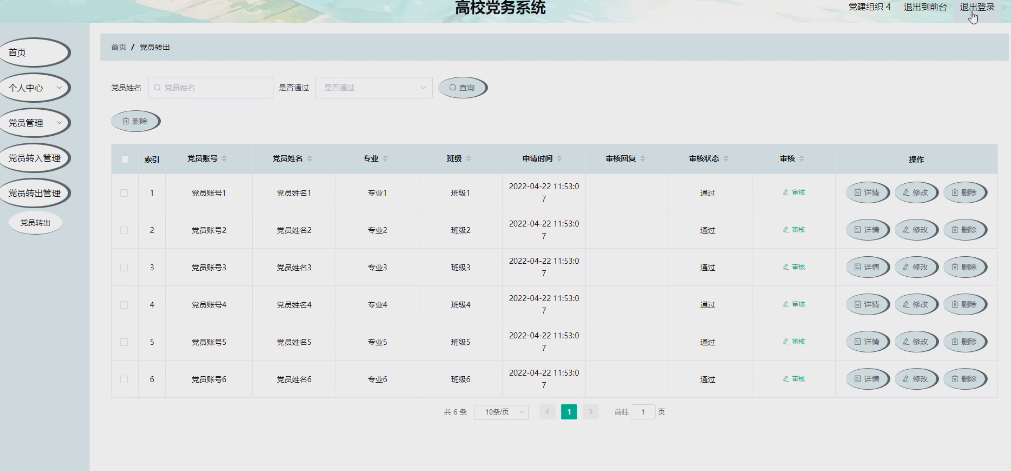
基于springboot实现高校党务平台管理系统【项目源码】计算机毕业设计
基于springboot实现高校党务平台管理系统演示 Java技术 Java是由Sun公司推出的一门跨平台的面向对象的程序设计语言。因为Java 技术具有卓越的通用性、高效性、健壮的安全性和平台移植性的特点,而且Java是开源的,拥有全世界最大的开发者专业社群&#x…...
Day24力扣打卡
打卡记录 寻找峰值(二分法) class Solution { public:int findPeakElement(vector<int> &nums) {int left -1, right nums.size() - 1; // 开区间 (-1, n-1)while (left 1 < right) { // 开区间不为空int mid left (right - left) / …...

5G-A 商用加速,赋能工业互联网
2019 年 6 月,中国工业和信息化部发放 5G 商用牌照。同年 10 月,三大运营商公布 5G 商用套餐,11 月 1 日正式上线 5G 商用套餐,标志中国正式进入 5G 商用新纪元。今年是 5G 商用的第五年,在当前数字经济蓬勃发展的催化…...

代码随想录day2
目录 vscode 自定义代码模板Reference vscode 自定义代码模板 select User snippets from Settings on the bottom left corner. select a certain language for example: cpp create your own snippets 格式如下,防着写 第一行"cpp template",模板…...
UML/SysML建模工具更新(2023.10)(1)StarUML、Software Ideas Modeler
DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 工具最新版本:Software Ideas Modeler 14.02 更新时间:2023年10月9日 工具简介 轻量级建模工具,支持UML、BPMN、SysML。 平台:Windo…...
kubectl 资源管理命令-陈述式
目录 一、kubectl陈述式资源管理: 二、kubectl陈述式对象管理: 1.基础命令使用: 1.1 帮助手册: 1.2 查看版本信息: 编辑 1.3 查看资源对象简写: 1.4 查看集群信息: 1.5 配置kubectl自动补全: 1.6 node节点查看日志…...
【紫光同创国产FPGA教程】——【PGL22G第九章】HDMI环路实验例程
本原创教程由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处 适用于板卡型号: 紫光同创PGL22G开发平台(盘古22K) 一:盘古22K开发板(紫光同创PGL22G开…...
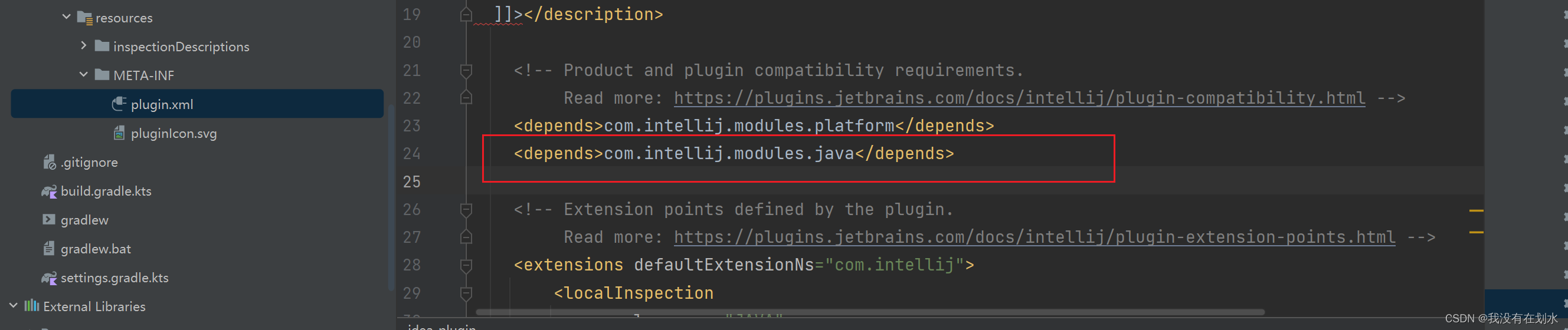
IDEA Plugin插件开发相关踩坑
1 前言 最近在研究IDEA插件开发,踩了不少坑,特意在这里记录一下…… 2 Java相关类找不到 照着网上一些资料,想要实现代码审计自动提示功能,需要继承AbstractBaseJavaLocalInspectionTool 结果import一片爆红,找不到相…...
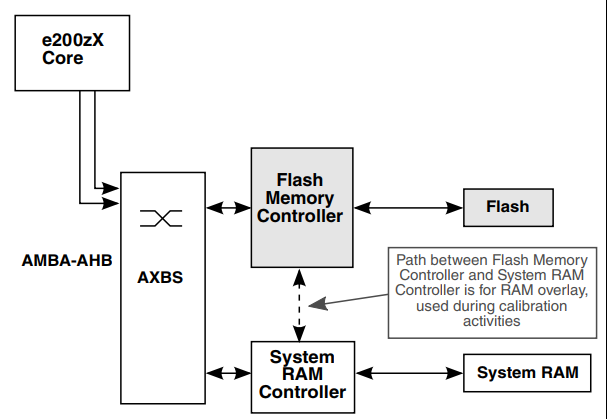
汽车标定技术(八)--MPC57xx是如何支持标定的页切换
目录 1.页切换的概念 1.1 标定常量的理解 1.2 页切换 2.MPC57xx的Overlay模块 3.小结 1.页切换的概念 在汽车标定测量中,有一个概念我想很多人都听过,但是实际上在项目里没有用到过,那就是今天要讲的页切换概念。在讲页切换的时候&#…...
Ubuntu中增加交换内存
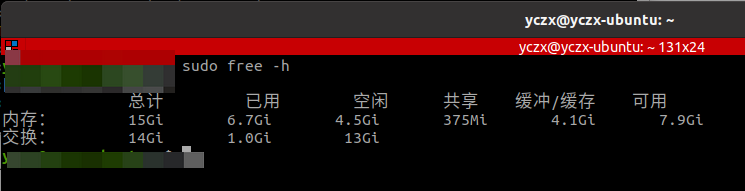
前言 在运行一些代码编译或者clang-format会占用大量的内存,此时可能会出现电脑卡死的情况,在ubuntu中可以通过增加交换内存来临时解决这个问题,相对于硬件改动成本更低,但是性能不如物理内存。 实践 查看当前的交换内存大小 …...

一文带您了解云渲染
很多刚刚接触云渲染的网友可能还不太了解云渲染,不知道云渲染是什么,不知道如何选择云渲染,不知道云渲染怎么收费,今天小编归纳总结了一些网友比较关心的问题,在本文中一一为大家解答。 云渲染是什么? 云…...

分享4个MSVCP100.dll丢失的解决方法
msvcp100.dll是一个重要的动态链接库文件,它是Microsoft Visual C 2010 Redistributable Package的一部分。这个文件的作用是提供在运行C程序时所需的函数和功能。如果计算机系统中msvcp100.dll丢失或者损坏,就会导致软件程序无法启动运行,会…...

国际腾讯云服务器流量收费准分析!!
腾讯云是腾讯公司供应的云核算服务,包含云服务器、云存储、数据库、CDN、安全等服务。本文将对腾讯云服务器流量收费标准进行具体的分析,协助用户了解腾讯云服务器的运用本钱。 腾讯云服务器流量收费标准首要分为包年包月、按需付费和按流量付费三种办法…...
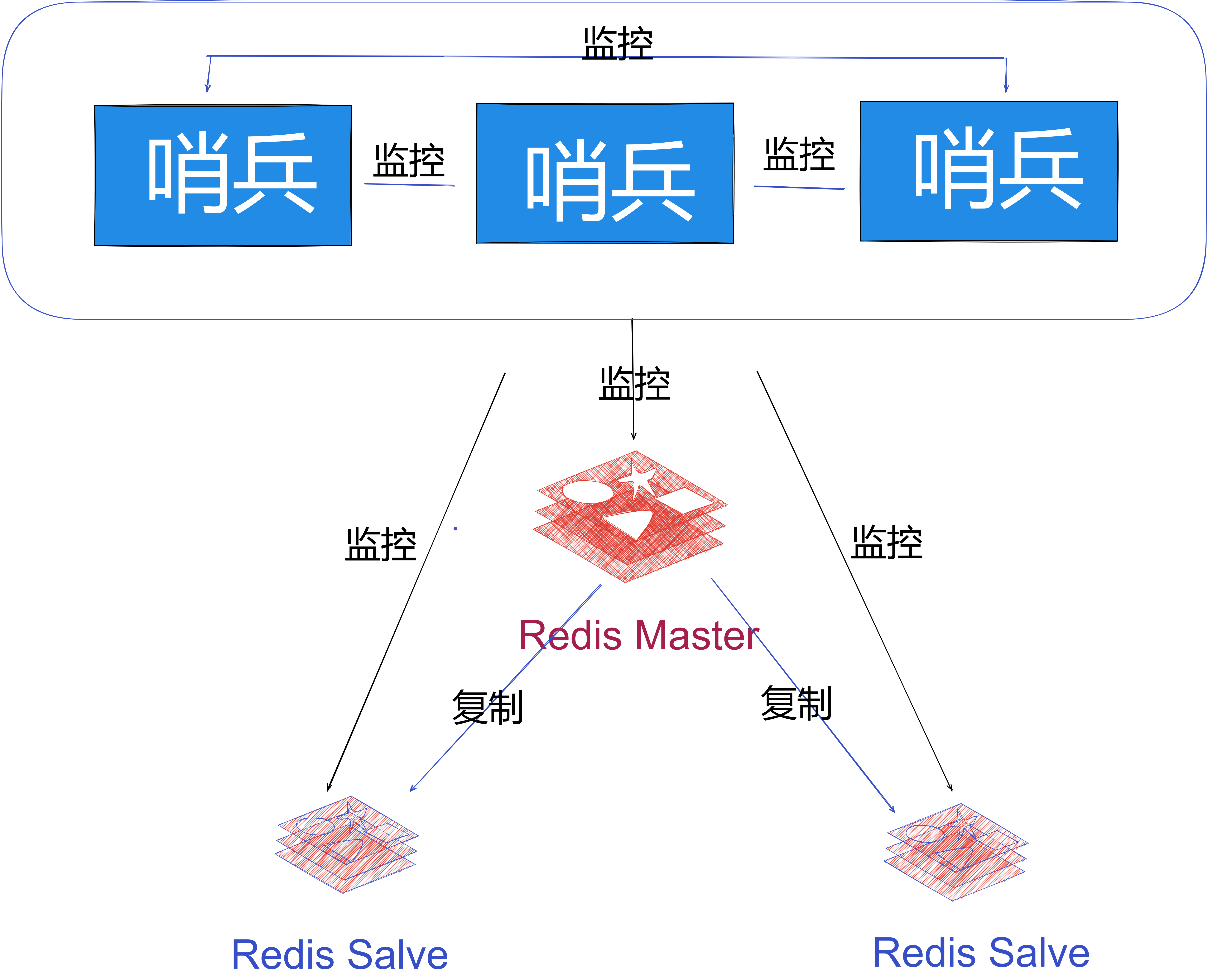
Redis系列-四种部署方式-单机部署+主从模式+哨兵模式【7】
目录 Redis系列-四种部署方式-单机部署主从模式【7】redis-四种部署模式单机模式主从模式数据同步的方式全量数据同步增量数据同步 Redis哨兵模式总结缺点:哨兵模式应用sentinel.conf配置项 REF 个人主页: 【⭐️个人主页】 需要您的【💖 点赞关注】支持…...

Webpack 的作用和工作原理是什么?
Webpack 是一个现代的静态模块打包工具,它的作用是将前端应用程序的各种资源(如 JavaScript、CSS、图片等)视为模块,并将它们打包成可以在浏览器中运行的静态文件。它的主要功能包括模块打包、资源优化、代码分割、加载器转换等。…...
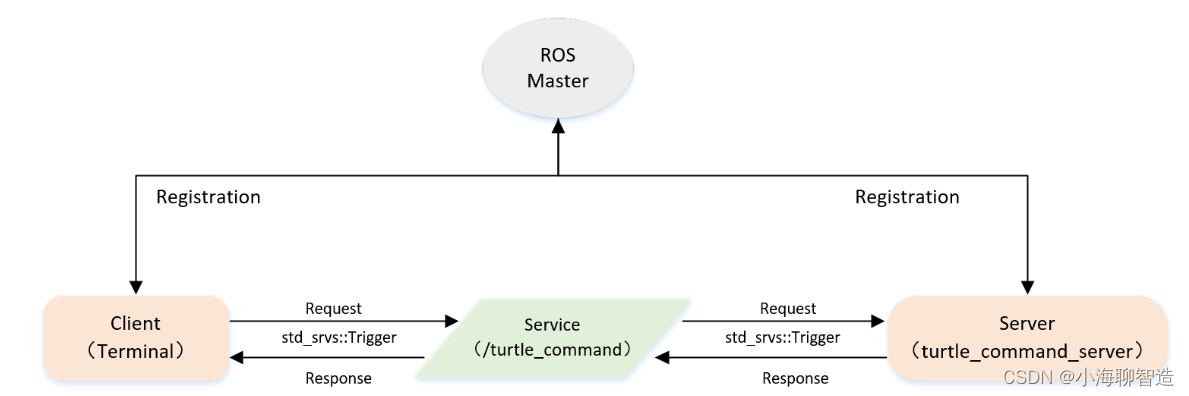
ros1 实现Server端自定义四 Topic模式控制海龟运动
一、服务模型 Server端本身是进行模拟海龟运动的命令端,它的实现是通过给海龟发送速度(Twist)的指令,来控制海龟运动(本身通过Topic实现)。 Client端相当于海龟运动的开关,其发布Request来控制…...
 版本 Git 如何找回被 Drop Commit 的提交记录)
IntelliJ IDEA 2023.2.1 (Ultimate Edition) 版本 Git 如何找回被 Drop Commit 的提交记录
本心、输入输出、结果 文章目录 IntelliJ IDEA 2023.2.1 (Ultimate Edition) 版本 Git 如何找回被 Drop Commit 的提交记录前言查询 reflog 日志通过 Git Reset HEAD (hard) 找回已经 Drop Commit 的提交记录Git Reset HEAD (hard) 模式和 mixed 模式有啥区别git reset --h…...
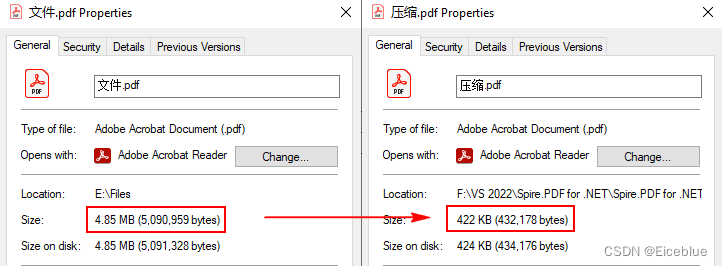
C# 压缩PDF文件
PDF 文件可以包含文本、图片及各种媒体元素,但如果文件太大则会影响传输效果同时也会占用过多磁盘空间。通过压缩PDF文件,能够有效减小文件大小,从而提高传输效率并节省存储空间。想要通过C#代码快速有效地压缩 PDF 文件,下面是实…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
