当前位置： 首页 > news >正文

表象变换与矩阵元

news 2026/2/9 3:28:53
  • 表象变换

一维粒子哈密顿量H=\frac{p^2}{2m}+V(x)

x表象中x,p,H的矩阵元

(x)_{x'x''}=\left \langle x'| x|x''\right \rangle=\int\delta(x-x')x\delta(x-x'')dx=x'\delta(x'-x'')

  • 态的表象变换

F:<k|\varphi>=a_k;F':<\alpha|\varphi>=a_\alpha

<a|\varphi>=\sum_k<a|k><k|\varphi>=\sum_kS_{\alpha k}a_k

  • 不难证明S^+S=SS^+=I
  • 算符的表象变换

L_{jk}=<j|\hat{L}|k>

  • 坐标表象

<x|p'>=\frac{1}{\sqrt{2\pi\hbar}}exp(ip'/\hbar)

Non-denumerable basis

  1. <x|y>=\delta(x-y)
  2. \hat{x}|x>=x|x>
  3. \hat{x}^\dagger=\hat{x}\Rightarrow <x|\hat{x}=x<x|
  4. \hat{p}^\dagger=\hat{p}\Rightarrow <p|\hat{p}=p<p|
  5. p|x>=\hat{p}<x|=\frac{\hbar}{i}\frac{\partial}{\partial x}<x|
  6. <\phi|\psi>=\int dx<\phi|x><x|\psi>=\int dx \phi^*(x)\psi(x)
  7. <\phi|\hat{x}|\psi>=<\phi|\hat{x}\hat{1}|\psi>=\int dx<\phi|\hat{x}|x><x|\psi>=\int dx <\phi|x>x<x|\psi>=\int dx\phi^*(x)x\psi(x)
  8. <x|p>=\frac{e^{ipx/\hbar}}{\sqrt{2\pi\hbar}}
  9. \frac{1}{2\pi}\int due^{i(p-p')u}=\delta(p-p')

相关文章：

表象变换与矩阵元

表象变换 一维粒子哈密顿量 表象中的矩阵元 态的表象变换 不难证明 算符的表象变换 坐标表象 Non-denumerable basis...

编程日记 2023/11/9 20:36:47

vue乾坤微前端项目

1、主应用 安装乾坤 npm i qiankun -S 注册微应用并启动&#xff1a; import { registerMicroApps, start } from qiankun;//设置两个微应用 registerMicroApps([{name: vue1, //要跟package.json中的name保持一致entry: //localhost:8081, //本地就这么写container: #cont…...

编程日记 2023/11/9 20:35:46

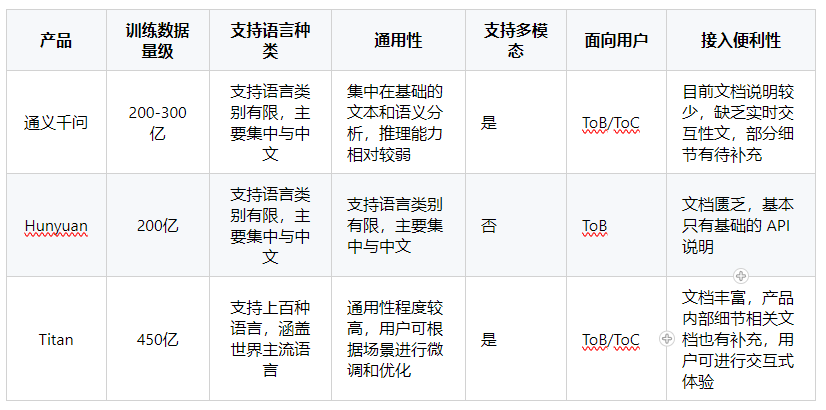
大语言模型比武

今年随着 ChatGPT 的流行&#xff0c;并在各个领域有一定程度生产级别的应用。国内外也掀起了一股大语言模型浪潮&#xff0c;各大厂商都推出了自己的大语言模型&#xff0c;阿里推出了 通义千问&#xff0c;腾讯推出了 Hunyuan&#xff0c;亚马逊云推出了 Titan&#xff0c;大…...

编程日记 2023/11/9 20:34:41

王道数据结构第五章二叉树的遍历第13题

目录 解题思路 宏定义 二叉树定义 栈定义 实现函数 测试代码 测试结果...

编程日记 2023/11/9 20:33:39

微服务的发展历程的详细说明及每个阶段主流的架构和组件

微服务的发展历程的详细说明及每个阶段主流的架构和组件如下&#xff1a; 一、微服务的发展历程&#xff1a; 起始阶段&#xff1a;这个阶段主要是面向服务的架构&#xff08;SOA&#xff09;的兴起。此时&#xff0c;企业开始尝试将单体应用拆分为多个服务&#xff0c;但此时…...

编程日记 2023/11/9 20:32:38

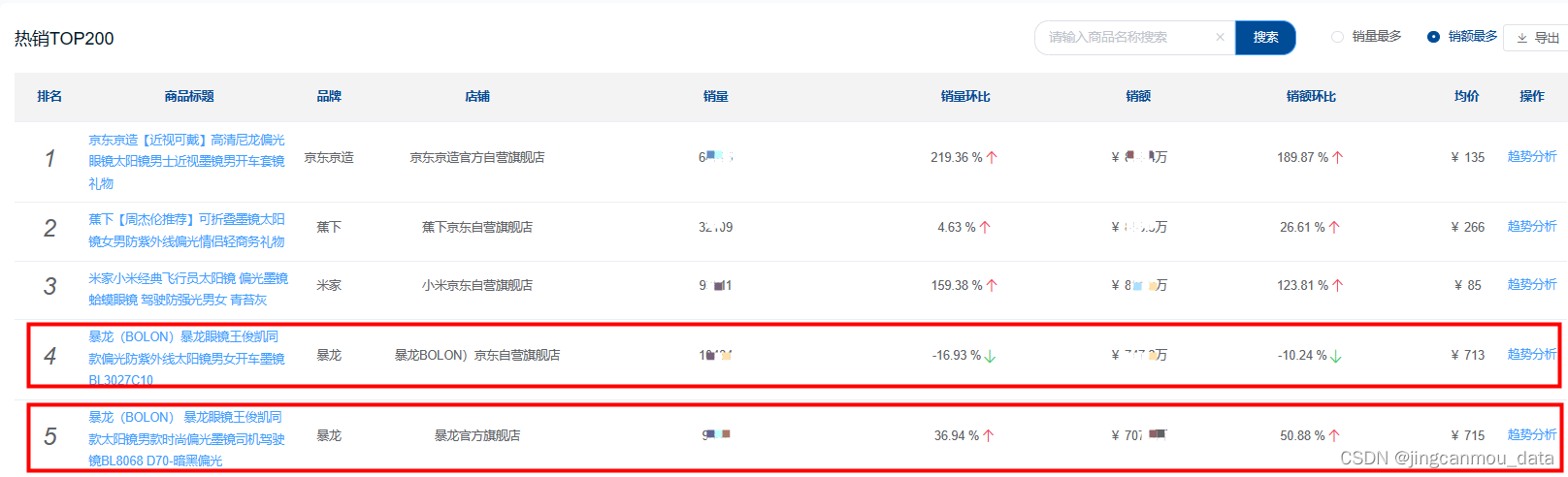
2023年眼镜行业分析（京东眼镜销量数据分析）：市场规模同比增长26%，消费需求持续释放

随着我国经济的不断发展&#xff0c;电子产品不断普及&#xff0c;低龄及老龄人口的用眼场景不断增多&#xff0c;不同年龄阶段的人群有不同的视力问题&#xff0c;因此&#xff0c;视力问题人口基数也随之不断加大&#xff0c;由此佩戴眼镜的人群也不断增多。 同时&#xff0c…...

编程日记 2023/11/9 20:31:37

基础课26——业务流程分析方法论

基础课25中我们提到业务流程分析方法包括以下几种&#xff1a; 价值链分析法&#xff1a;主要是找出或设计出哪些业务能够使得客户满意&#xff0c;实现客户价值最大化的业务流程。要进行价值链分析的时候可以从企业具体的活动进行细分&#xff0c;细分的具体方面可以从生产指…...

编程日记 2023/11/9 20:30:37

【数字图像处理-TUST】实验二-图像噪声生成与滤波降噪

一&#xff0c;题目 读入一幅图像使用两种以上的方法向图像中分别添加噪声输出一幅二值图像&#xff0c;背景为黑色&#xff0c;噪声区域为白色使用三种滤波方法对上述添加了噪声的图像进行降噪处理输出降噪处理后的结果图像 二&#xff0c;实验原理 采用了两种方法添加了噪…...

编程日记 2023/11/9 20:29:36

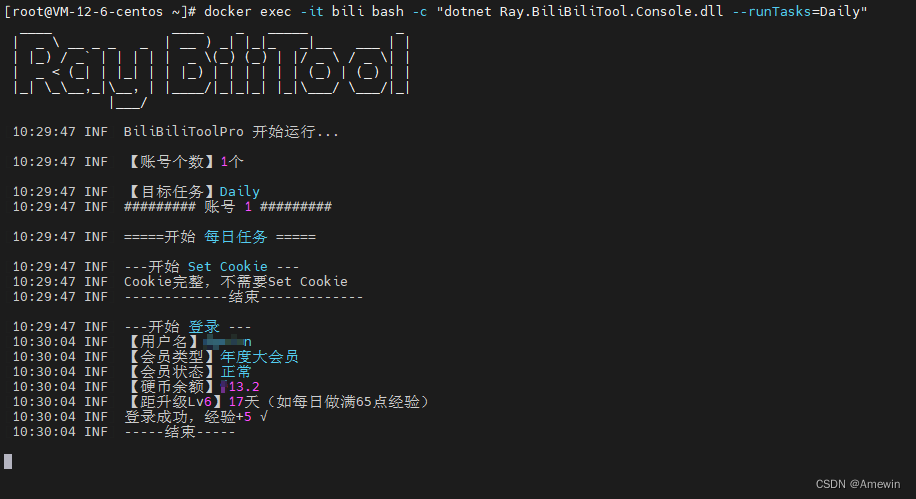
bilibili快速升满级(使用Docker 容器脚本)

部署bilibili升级运行容器脚本 docker run --name"bili" -v /bili/Logs:/app/Logs -e Ray_DailyTaskConfig__Cron"30 9 * * *" -e Ray_LiveLotteryTaskConfig__Cron"40 9 * * *" -e Ray_UnfollowBatchedTaskConfig__Cron"…...

编程日记 2023/11/9 20:27:33

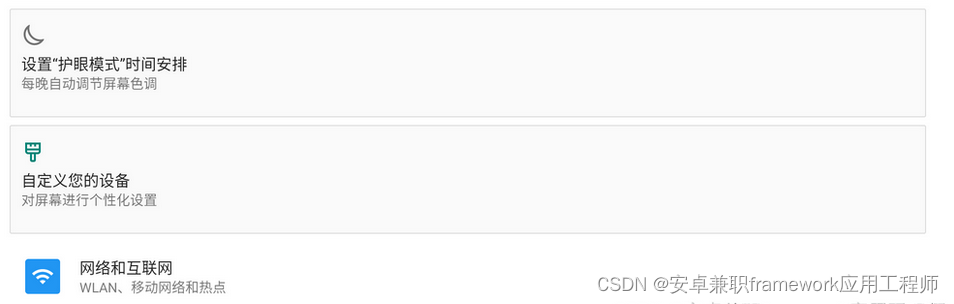
Android 13.0 Settings主页面去掉FocusRecyclerView相关功能

1.前言 在13.0的系统rom产品定制化开发中，在系统Settings主页面的主菜单中，在测试某些功能的时候，比如开启护眼模式和改变系统密度会在主菜单第一项的网络菜单头部增加 自定义您的设备和设置护眼模式时间安排 等等相关的设置模块 这对于菜单布局显示相当不美观，所以根据系…...

编程日记 2023/11/9 20:26:30

Python（四）字符串

程序员的公众号&#xff1a;源1024&#xff0c;获取更多资料&#xff0c;无加密无套路&#xff01; 最近整理了一波电子书籍资料&#xff0c;包含《Effective Java中文版 第2版》《深入JAVA虚拟机》&#xff0c;《重构改善既有代码设计》&#xff0c;《MySQL高性能-第3版》&…...

编程日记 2023/11/9 20:25:29

WPF中ElementName与RelativeSource绑定的局限性以及对策

完全来源于十月的寒流&#xff0c;感谢大佬讲解 <Window x:Class"Test_01.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schem…...

编程日记 2023/11/9 20:24:28

基于PHP语言的会员系统搭建（Docker版）

1、操作系统 准备&#xff1a; ubuntu22机器 基础&#xff1a;docker:【精选】Docker微服务-基础_v2/_catalog-CSDN博客 2、安装Docker # Add Dockers official GPG key: sudo apt-get update sudo apt-get install ca-certificates curl gnupg sudo install -m 0755 -d /etc/…...

编程日记 2023/11/9 20:22:24

文件改名：一次性解决文件名混乱，批量重命名技巧

在日常生活和工作中&#xff0c;我们经常会遇到文件名混乱的问题&#xff0c;例如文件名重复、格式不统一或者文件名错误等。这些问题不仅会给我们带来查找和使用上的困扰&#xff0c;还会影响我们的工作效率。为了解决这些问题&#xff0c;我们可以使用批量重命名技巧&#xf…...

编程日记 2023/11/9 20:21:23

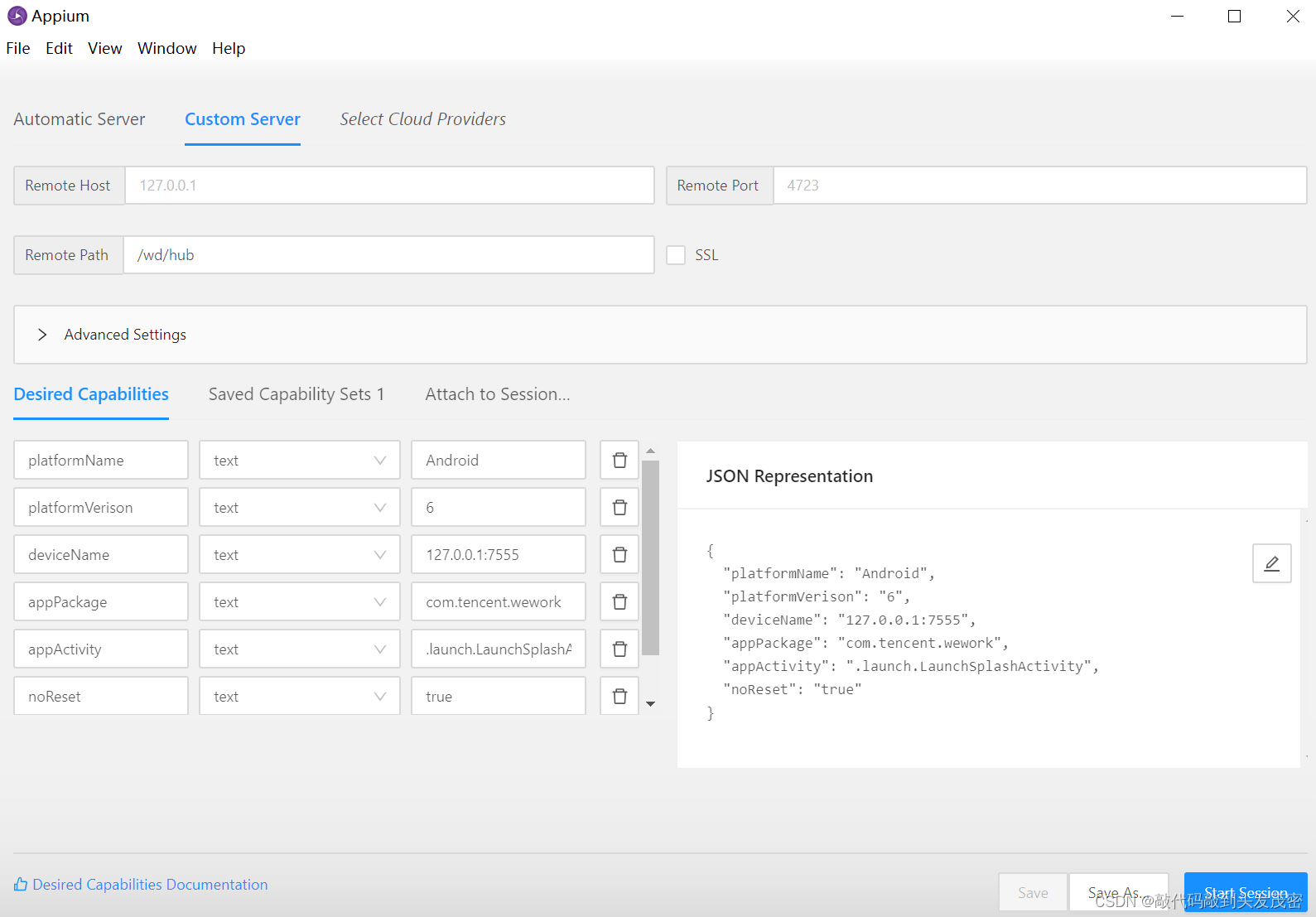
app自动化测试——capability 配置参数解析

一、Capability 简介 功能&#xff1a;配置 Appium 会话&#xff0c;告诉 Appium 服务器需要自动化的平台的应用程序 形式&#xff1a;键值对的集合&#xff0c;键对应设置的名称&#xff0c;值对应设置的值 主要分为三部分 公共部分 ios 部分 android 部分 二、Session Appi…...

编程日记 2023/11/9 20:20:22

数仓面经大框架

1.计算机及编程基础&#xff1a; 操作系统&#xff1a;进程、线程等 数据结构&#xff1a;算法题 计算机网络&#xff1a;分层等 Linux&#xff1a;常用的指令 MySQL&#xff08;重点&#xff09; Java/Python基础 排序算法&#xff08;快排、归并等&#xff09; 2.大数…...

编程日记 2023/11/9 20:19:21

C++ explicit关键字的作用

explicit关键字只针带一个参数的构造函数有效 #include <iostream> using namespace std;class A { public:A(int temp) //普通构造函数{a temp;cout << "普通构造函数: a " << a << endl;}A(const A &temp) //拷贝构造函数{a temp.a…...

编程日记 2023/11/9 20:18:19

排序算法之-冒泡

顺序排序算法原理 从头开始遍历未排序数列&#xff0c;遍历时比较相邻的两个元素&#xff0c;前面的大于后面的&#xff0c;则双方交换位置&#xff0c;一直比较到末尾&#xff0c;这样最大的元素会出现在末尾&#xff0c;接着再依次从头开始遍历剩余未排序的元素&#xff0c;…...

编程日记 2023/11/9 20:17:18

【微服务】API治理发展历史与未来趋势

目录 一、前言 二、API治理的价值和意义 2.1 API治理概念 2.2 API治理价值和意义 2.2.1 提升团队协同效率 2.2.2 降低产品运维成本 2.2.3 识别和降低系统的外部风险 2.2.4 提供更多的拓展性 三、API生命周期管理 ​编辑 3.1 规划阶段 3.2 开发阶段 3.3 测试阶段 3…...

编程日记 2023/11/9 20:15:16

TikTok shop美国小店适合哪些人做？附常见运营问题解答

一、Tiktok shop小店分类 大家都知道&#xff0c;美国小店可以分为5 种&#xff1a; 美国本土个人店: 最灵活&#xff0c;有扶持政策&#xff1b;美国法人企业店&#xff1a;要求高&#xff0c;有扶持政策&#xff1b;美国公司中国人占股店 (ACCU店) : 权重相对低&#xff0c…...

编程日记 2023/11/9 20:14:15

【项目实战】通过多模态+LangGraph实现PPT生成助手

PPT自动生成系统 基于LangGraph的PPT自动生成系统&#xff0c;可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析&#xff1a;自动解析Markdown文档结构PPT模板分析&#xff1a;分析PPT模板的布局和风格智能布局决策&#xff1a;匹配内容与合适的PPT布局自动…...

编程新知 2026/2/3 22:50:07

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法（ISWC2024）

笔记整理&#xff1a;刘治强&#xff0c;浙江大学硕士生&#xff0c;研究方向为知识图谱表示学习&#xff0c;大语言模型 论文链接&#xff1a;http://arxiv.org/abs/2407.16127 发表会议&#xff1a;ISWC 2024 1. 动机 传统的知识图谱补全&#xff08;KGC&#xff09;模型通过…...

编程新知 2026/1/31 12:03:23

现代密码学 | 椭圆曲线密码学—附py代码

Elliptic Curve Cryptography 椭圆曲线密码学&#xff08;ECC&#xff09;是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础&#xff0c;例如椭圆曲线数字签…...

编程新知 2026/2/6 7:30:33

CSS设置元素的宽度根据其内容自动调整

width: fit-content 是 CSS 中的一个属性值&#xff0c;用于设置元素的宽度根据其内容自动调整&#xff0c;确保宽度刚好容纳内容而不会超出。 效果对比 默认情况&#xff08;width: auto&#xff09;&#xff1a; 块级元素&#xff08;如 <div>&#xff09;会占满父容器…...

编程新知 2025/10/16 16:03:09

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/1/26 9:30:45

MySQL 知识小结（一）

一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库&#xff0c;分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷&#xff0c;但是文件存放起来数据比较冗余&#xff0c;用二进制能够更好管理咱们M…...

编程新知 2026/1/26 13:29:47

LangFlow技术架构分析

&#x1f527; LangFlow 的可视化技术栈 前端节点编辑器 底层框架&#xff1a;基于 &#xff08;一个现代化的 React 节点绘图库&#xff09; 功能&#xff1a; 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

编程新知 2025/6/10 21:26:51

vue3 daterange正则踩坑

<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

编程新知 2025/12/27 19:12:09

Ubuntu系统多网卡多相机IP设置方法

目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机&#xff0c;交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息&#xff0c;系统版本&#xff1a;Ubuntu22.04.5 LTS&#xff1b;内核版本…...

编程新知 2026/2/4 16:40:55