常用的三角函数公式
-
sin 2 x + cos 2 x = 1 \sin ^2 x + \cos ^2 x = 1 sin2x+cos2x=1
-
tan x = sin x cos x \tan x = \dfrac{\sin x}{\cos x} tanx=cosxsinx
-
cot x = 1 tan x = cos x sin x \cot x = \dfrac{1}{\tan x}=\dfrac{\cos x}{\sin x} cotx=tanx1=sinxcosx
-
sec x = 1 cos x \sec x= \dfrac{1}{\cos x} secx=cosx1
-
csc x = 1 sin x \csc x =\dfrac{1}{\sin x} cscx=sinx1
-
tan 2 x = sec 2 − 1 = 1 cos 2 x − 1 = 1 − cos 2 x cos 2 x = sin 2 x cos 2 x \tan^2x=\sec^2-1=\dfrac{1}{\cos^2x}-1=\dfrac{1-\cos^2x}{\cos^2x}=\dfrac{\sin^2x}{\cos^2x} tan2x=sec2−1=cos2x1−1=cos2x1−cos2x=cos2xsin2x
-
cot 2 = csc 2 x − 1 = 1 sin 2 x − 1 = 1 − sin 2 x sin 2 x = cos 2 x sin 2 x \cot^2=\csc^2x-1=\dfrac{1}{\sin^2x}-1=\dfrac{1-\sin^2x}{\sin^2x}=\dfrac{\cos^2x}{\sin^2x} cot2=csc2x−1=sin2x1−1=sin2x1−sin2x=sin2xcos2x
-
cos x = sin ( x + π 2 ) \cos x=\sin(x+\dfrac{\pi}{2}) cosx=sin(x+2π), sin x \sin x sinx 向左平移 π 2 \dfrac{\pi}{2} 2π. (左加右减)
-
sin x = cos ( x − π 2 ) \sin x=\cos(x-\dfrac{\pi}{2}) sinx=cos(x−2π)
-
cos x = cos ( − x ) \cos x= \cos(-x) cosx=cos(−x),偶函数
-
sin x = − sin ( − x ) \sin x = - \sin(-x) sinx=−sin(−x),奇函数
-
sin x = − sin ( x ± π ) \sin x= -\sin(x\pm\pi) sinx=−sin(x±π), sin x \sin x sinx无论是向左、还是向右平移 π \pi π 个单位后,乘以-1,关于x轴对称之后函数图像不变.
-
cos x = − cos ( x ± π ) \cos x = -\cos(x\pm\pi) cosx=−cos(x±π)
-
arcsin x + arccos x = π 2 \arcsin x+\arccos x=\dfrac{\pi}{2} arcsinx+arccosx=2π.
倍(半)角公式
-
cos ( A ± B ) = cos A ⋅ cos B ∓ sin A ⋅ sin B \cos(A\pm B)=\cos A\cdot\cos B \mp \sin A\cdot\sin B cos(A±B)=cosA⋅cosB∓sinA⋅sinB.
-
sin ( A ± B ) = sin A ⋅ cos B ± cos A ⋅ sin B \sin(A\pm B)=\sin A\cdot\cos B \pm \cos A\cdot\sin B sin(A±B)=sinA⋅cosB±cosA⋅sinB.
-
cos ( 2 A ) = cos 2 A − sin 2 A = 1 − 2 sin 2 A = 2 cos 2 A − 1 \cos(2A)=\cos^2A-\sin^2A=1-2\sin^2A=2\cos^2A-1 cos(2A)=cos2A−sin2A=1−2sin2A=2cos2A−1.
-
cos A = cos 2 A 2 − sin 2 A 2 = 1 − 2 sin 2 A 2 = 2 cos 2 A 2 − 1 \cos A = \cos^2\dfrac{A}{2}-\sin^2\dfrac{A}{2}=1-2\sin^2\dfrac{A}{2}=2\cos^2\dfrac{A}{2}-1 cosA=cos22A−sin22A=1−2sin22A=2cos22A−1.
-
sin ( 2 A ) = 2 sin A ⋅ cos A \sin(2A)=2\sin A\cdot\cos A sin(2A)=2sinA⋅cosA.
-
sin A = 2 sin A 2 ⋅ cos A 2 \sin A = 2\sin\dfrac{A}{2}\cdot\cos\dfrac{A}{2} sinA=2sin2A⋅cos2A.
-
tan 2 α = 2 tan α 1 − tan 2 α \tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^2\alpha} tan2α=1−tan2α2tanα.
-
tan α = 2 tan α 2 1 − tan 2 α 2 \tan\alpha=\dfrac{2\tan\dfrac{\alpha}{2}}{1-\tan^2\dfrac{\alpha}{2}} tanα=1−tan22α2tan2α.
-
tan α 2 = 1 − cos α sin α = sin α 1 + cos α \tan\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{\sin\alpha}=\dfrac{\sin\alpha}{1+\cos\alpha} tan2α=sinα1−cosα=1+cosαsinα.
tan 2 α = sin 2 α cos 2 α = 2 sin α ⋅ cos α 1 − 2 sin 2 α = 2 tan α 1 cos 2 α − 2 tan 2 α = 2 tan α 1 − sin 2 α cos 2 α − tan 2 α = 2 tan α 1 − tan 2 α . \tan2\alpha=\dfrac{\sin2\alpha}{\cos2\alpha}=\dfrac{2\sin\alpha\cdot\cos\alpha}{1-2\sin^2\alpha}=\dfrac{2\tan\alpha}{\dfrac{1}{\cos^2\alpha}-2\tan^2\alpha}=\dfrac{2\tan\alpha}{\dfrac{1-\sin^2\alpha}{\cos^2\alpha}-\tan^2\alpha}=\dfrac{2\tan\alpha}{1-\tan^2\alpha}. tan2α=cos2αsin2α=1−2sin2α2sinα⋅cosα=cos2α1−2tan2α2tanα=cos2α1−sin2α−tan2α2tanα=1−tan2α2tanα.
tan α = 2 tan α 2 1 − tan 2 α 2 \tan\alpha=\dfrac{2\tan\dfrac{\alpha}{2}}{1-\tan^2\dfrac{\alpha}{2}} tanα=1−tan22α2tan2α
tan α − tan α tan 2 α 2 = 2 tan α 2 \tan\alpha-\tan\alpha\tan^2\dfrac{\alpha}{2}=2\tan\dfrac{\alpha}{2} tanα−tanαtan22α=2tan2α
tan α ⋅ tan 2 α 2 + 2 tan α 2 − tan α = 0 \tan\alpha\cdot\tan^2\dfrac{\alpha}{2}+2\tan\dfrac{\alpha}{2}-\tan\alpha=0 tanα⋅tan22α+2tan2α−tanα=0
求根公式:
tan α 2 = − 2 ± 4 + 4 tan 2 α 2 tan α = − 1 ± sec α tan α = − cos α ± 1 sin α \tan\dfrac{\alpha}{2}=\dfrac{-2\pm\sqrt{4+4\tan^2\alpha}}{2\tan\alpha}=\dfrac{-1\pm\sec\alpha}{\tan\alpha}=\dfrac{-\cos\alpha\pm1}{\sin\alpha} tan2α=2tanα−2±4+4tan2α=tanα−1±secα=sinα−cosα±1
当 α ∈ ( 0 , π ) \alpha\in(0,\pi) α∈(0,π) 时, tan α 2 > 0 \tan\dfrac{\alpha}{2}>0 tan2α>0,而 − cos α + 1 sin α < 0 -\dfrac{\cos\alpha+1}{\sin\alpha}<0 −sinαcosα+1<0.
∴ tan α 2 = − cos α + 1 sin α \therefore \tan\dfrac{\alpha}{2}=-\dfrac{\cos\alpha+1}{\sin\alpha} ∴tan2α=−sinαcosα+1 不成立.
∴ tan α 2 = 1 − cos α sin α = ( 1 − cos α ) ⋅ ( 1 + cos α ) sin α + sin α ⋅ cos α = 1 − cos 2 α sin α + sin α ⋅ cos α = sin α 1 + cos α \therefore \tan\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{\sin\alpha}=\dfrac{(1-\cos\alpha)\cdot(1+\cos\alpha)}{\sin\alpha+\sin\alpha\cdot\cos\alpha}=\dfrac{1-\cos^2\alpha}{\sin\alpha+\sin\alpha\cdot\cos\alpha}=\dfrac{\sin\alpha}{1+\cos\alpha} ∴tan2α=sinα1−cosα=sinα+sinα⋅cosα(1−cosα)⋅(1+cosα)=sinα+sinα⋅cosα1−cos2α=1+cosαsinα
正、余弦化切弦
-
sin 2 x = 2 sin x ⋅ cos x = 2 tan x sec 2 x = 2 tan x 1 + tan 2 x \sin2x=2\sin x\cdot\cos x=\dfrac{2\tan x}{\sec^2x}=\dfrac{2\tan x}{1+\tan^2x} sin2x=2sinx⋅cosx=sec2x2tanx=1+tan2x2tanx.
-
cos 2 x = cos 2 x − sin 2 x = 1 − tan 2 x sec 2 x = 1 − tan 2 x 1 + tan 2 x \cos2x=\cos^2x-\sin^2x=\dfrac{1-\tan^2x}{\sec^2x}=\dfrac{1-\tan^2x}{1+\tan^2x} cos2x=cos2x−sin2x=sec2x1−tan2x=1+tan2x1−tan2x.
-
sin x = 2 tan x 2 1 + tan 2 x 2 \sin x=\dfrac{2\tan\dfrac{x}{2}}{1+\tan^2\dfrac{x}{2}} sinx=1+tan22x2tan2x.
-
cos x = 1 − tan 2 x 2 1 + tan 2 x 2 \cos x=\dfrac{1-\tan^2\dfrac{x}{2}}{1+\tan^2\dfrac{x}{2}} cosx=1+tan22x1−tan22x.
辅助角公式
- sin α ⋅ a a 2 + b 2 − cos α ⋅ b a 2 + b 2 = sin α ⋅ cos β − cos α ⋅ sin β = sin ( α − β ) \sin\alpha\cdot\dfrac{a}{\sqrt{a^2+b^2}}-\cos\alpha\cdot\dfrac{b}{\sqrt{a^2+b^2}}=\sin\alpha\cdot\cos\beta-\cos\alpha\cdot\sin\beta=\sin(\alpha-\beta) sinα⋅a2+b2a−cosα⋅a2+b2b=sinα⋅cosβ−cosα⋅sinβ=sin(α−β).
其中,令 cos β = a a 2 + b 2 \cos\beta=\dfrac{a}{\sqrt{a^2+b^2}} cosβ=a2+b2a, sin β = b a 2 + b 2 \sin\beta=\dfrac{b}{\sqrt{a^2+b^2}} sinβ=a2+b2b,
则有 cos 2 β + sin 2 β = ( a a 2 + b 2 ) 2 + ( b a 2 + b 2 ) 2 = 1 \cos^2\beta+\sin^2\beta=\Big(\dfrac{a}{\sqrt{a^2+b^2}}\Big)^2+\Big(\dfrac{b}{\sqrt{a^2+b^2}}\Big)^2=1 cos2β+sin2β=(a2+b2a)2+(a2+b2b)2=1.
E m L 2 ω 2 + R 2 ⋅ ( R ⋅ sin ω t − L ω ⋅ cos ω t ) \dfrac{E_m}{L^2\omega^2+R^2}\cdot\big(R\cdot\sin\omega t-L\omega\cdot\cos\omega t\big) L2ω2+R2Em⋅(R⋅sinωt−Lω⋅cosωt)
= E m L 2 ω 2 + R 2 ⋅ ( sin ω t ⋅ R L 2 ω 2 + R 2 − cos ω t ⋅ L ω L 2 ω 2 + R 2 ) =\dfrac{E_m}{\sqrt{L^2\omega^2+R^2}}\cdot\big(\sin\omega t\cdot\dfrac{R}{\sqrt{L^2\omega^2+R^2}}-\cos\omega t\cdot\dfrac{L\omega}{\sqrt{L^2\omega^2+R^2}}\big) =L2ω2+R2Em⋅(sinωt⋅L2ω2+R2R−cosωt⋅L2ω2+R2Lω)
= E m L 2 ω 2 + R 2 ⋅ sin ( ω t − φ ) =\dfrac{E_m}{\sqrt{L^2\omega^2+R^2}}\cdot\sin(\omega t-\varphi) =L2ω2+R2Em⋅sin(ωt−φ).
其中 cos φ = R L 2 ω 2 + R 2 \cos\varphi=\dfrac{R}{\sqrt{L^2\omega^2+R^2}} cosφ=L2ω2+R2R, sin φ = L ω L 2 ω 2 + R 2 \sin\varphi=\dfrac{L\omega}{\sqrt{L^2\omega^2+R^2}} sinφ=L2ω2+R2Lω.
积化和差、和差化积
参考往期文章,点击跳转
相关文章:

常用的三角函数公式
sin 2 x cos 2 x 1 \sin ^2 x \cos ^2 x 1 sin2xcos2x1 tan x sin x cos x \tan x \dfrac{\sin x}{\cos x} tanxcosxsinx cot x 1 tan x cos x sin x \cot x \dfrac{1}{\tan x}\dfrac{\cos x}{\sin x} cotxtanx1sinxcosx sec …...

【MySQL】一文学会所有MySQL基础知识以及基本面试题
文章目录 前言 目录 文章目录 前言 一、主流数据库以及如何登陆数据库 二、常用命令使用 三、SQL分类 3.1 存储引擎 四、创建数据库如何设置编码等问题 4.1操纵数据库 4.2操纵表 五、数据类型 六、表的约束 七、基本查询 八、函数 九、复合查询 十、表的内连和外连 十一、索引…...
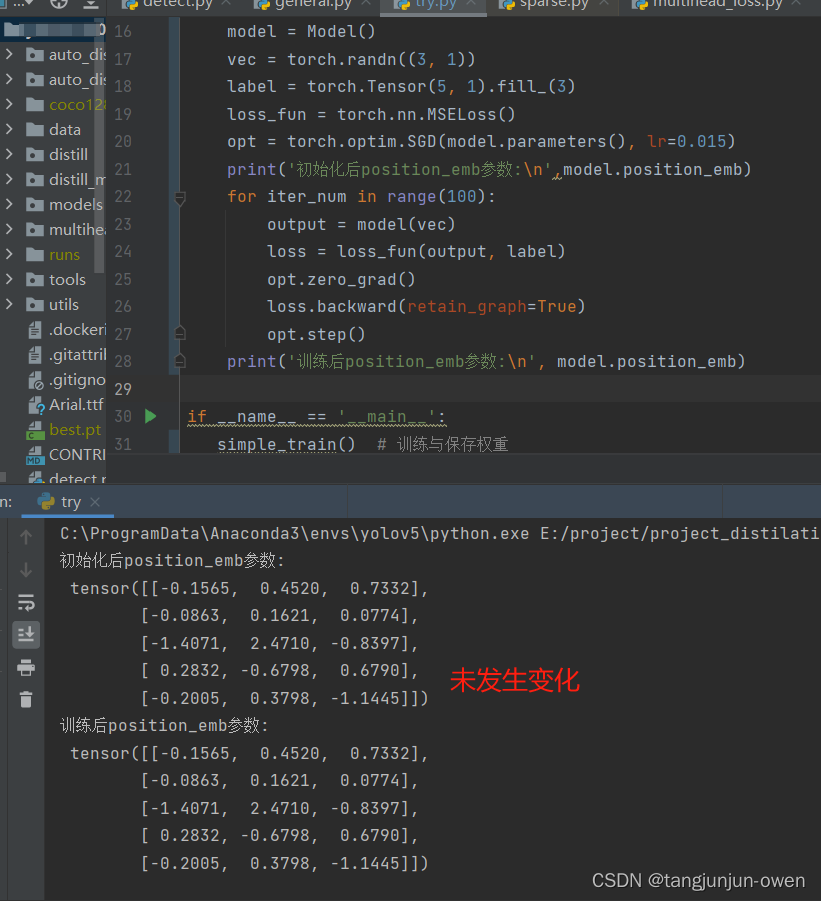
self.register_buffer方法使用解析(pytorch)
self.register_buffer就是pytorch框架用来保存不更新参数的方法。 列子如下: self.register_buffer("position_emb", torch.randn((5, 3)))第一个参数position_emb传入一个字符串,表示这组参数的名字,第二个就是tensor形式的参数…...
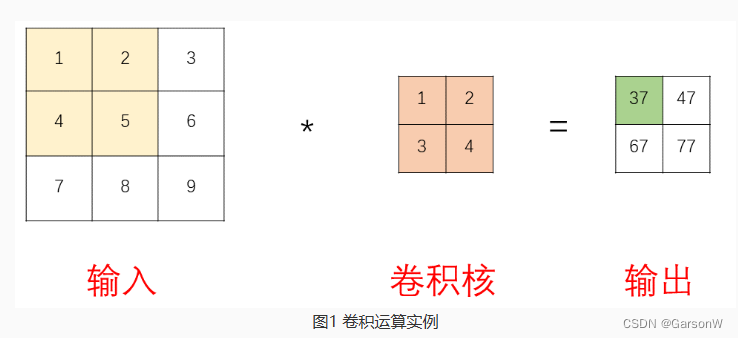
关于卷积神经网络中如何计算卷积核大小(kernels)
首先需要说明的一点是,虽然卷积层得名于卷积( convolution )运算,但我们通常在卷积层中使用更加直观的计算方式,叫做互相关( cross-correlation )运算。 也就是说,其实我们现在在这里…...
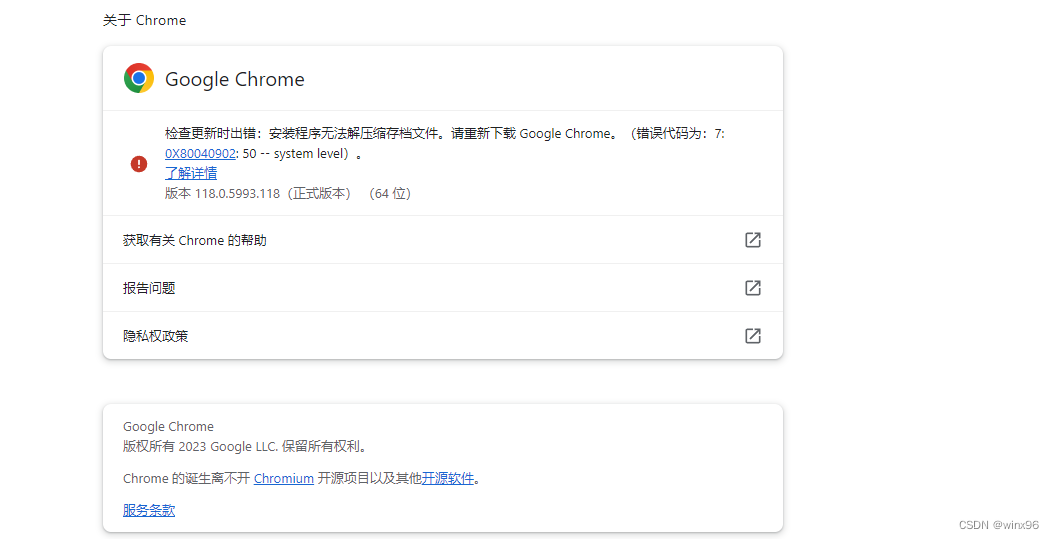
python使用selenium做自动化,最新版Chrome与chromedriver不兼容
目前Chrome版本是118.0.5993.118 下方是版本对应的下载地址: chrome版本118: https://download.csdn.net/download/qq_35845339/88510476 chrome版本119: chromedriverlinux64https://edgedl.me.gvt1.com/edgedl/chrome/chrome-for-testin…...

算法进阶指南图论 通信线路
通信线路 思路:我们考虑需要升级的那条电缆的花费,若其花费为 w ,那么从 1 到 n 的路径上,至多存在 k 条路径的价值大于 w ,这具有一定的单调性,当花费 w 越大,我们路径上价值大于 w 的花费会越…...
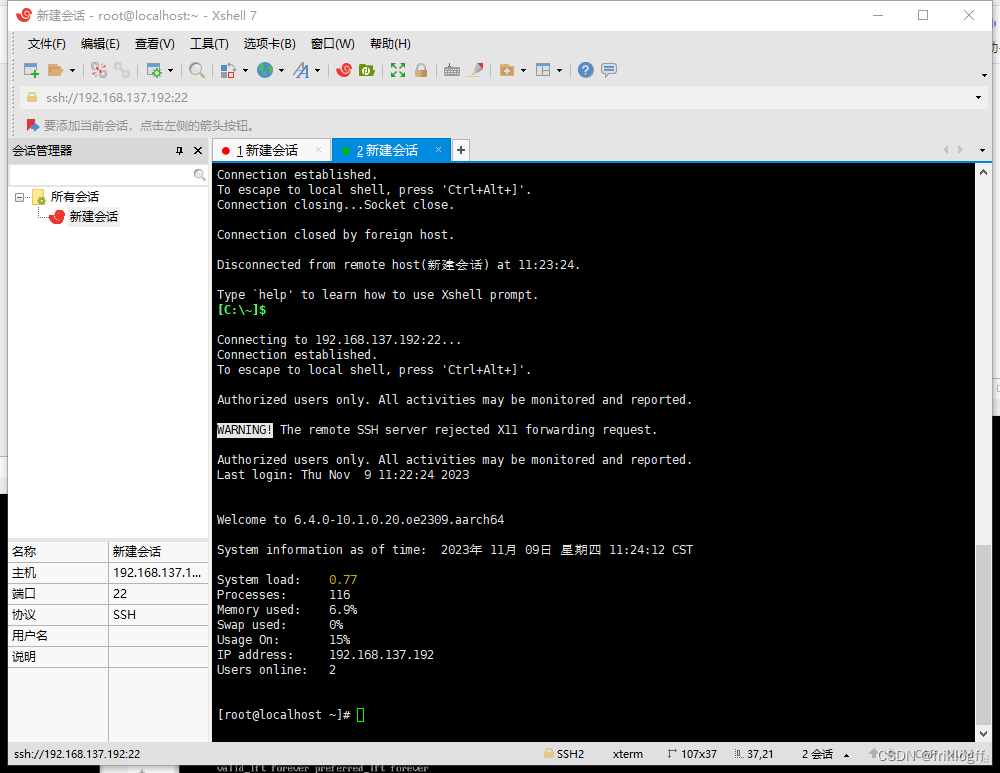
【QEMU-tap-windows-Xshell】QEMU 创建 aarch64虚拟机(附有QEMU免费资源)
“从零开始:在Windows上创建aarch64(ARM64)虚拟机” 前言 aarch64(ARM64)架构是一种现代的、基于 ARM 技术的计算架构,具有诸多优点,如低功耗、高性能和广泛应用等。为了在 Windows 平台上体验…...

strtok函数详解:字符串【分割】的利器
目录 一,strtok函数简介 二,strtok函数的用法 三,strtok函数的注意事项 一,strtok函数简介 strtok函数可以帮助我们将一个字符串按照指定的分隔符进行分割,从而得到我们想要的子字符串。 🍂函数头文件&am…...

winui3开发笔记(二)自定义标题栏
参考文章链接:https://www.programminghunter.com/article/46392310600/ 注意事项 获取 AppWindowTitleBar 的实例并设置其颜色属性时,InitializeTitleBar(AppWindow.TitleBar);,只适用于Windows App SDK 1.2及以上,所以如果用w…...

MapReduce 读写数据库
MapReduce 读写数据库 经常听到小伙伴吐槽 MapReduce 计算的结果无法直接写入数据库, 实际上 MapReduce 是有操作数据库实现的 本案例代码将实现 MapReduce 数据库读写操作和将数据表中数据复制到另外一张数据表中 准备数据表 create database htu; use htu; creat…...
)
设计模式 -- 状态模式(State Pattern)
状态模式:类的行为基于它的状态改变 属于行为型模式,创建表示各种状态的对象和一个行为随着状态对象改变而改变的 context 对象。在代码中包含大量与对象状态有关的条件语句可以通过此模式将各种具体的状态类抽象出来 介绍 意图:允许对象在…...

qt quick发布程序启动失败
qt quick/qml 程序发布之后,程序启动不了 经过探究测试,程序启动的不了的情况下是因为有dll没有添加。在release文件夹下进行发布操作(不单独复制xx.exe拿出来),再次点击IDE的RUN按钮,则会提示有Moudle没有…...

nginx反向代理报错合集
本文汇集了最近在使用nginx反向代理过程中遇到的一系列错误及其解决办法。 1缺乏支持项导致nginx配置错误 在利用sudo ./configure --with-http_ssl_module --with-http_stub_status_module进行配置时,往往会遇到以下类型的错误 error: the HTTP rewrite module …...

【Linux精讲系列】——vim详解
作者主页 📚lovewold少个r博客主页 ⚠️本文重点:c入门第一个程序和基本知识讲解 👉【C-C入门系列专栏】:博客文章专栏传送门 😄每日一言:宁静是一片强大而治愈的神奇海洋! 目录 目录 作者…...

微信小程序自动化采集方案
本文仅供学习交流,只提供关键思路不会给出完整代码,严禁用于非法用途,拒绝转载,若有侵权请联系我删除! 一、引言 1、对于一些破解难度大,花费时间长的目标,我们可以先采用自动化点击触发请求&…...

操作系统第三章王道习题_内存管理_总结易错知识点
1. 静态重定位和动态重定位 静态重定位(可重定位装入):作业在装入内存的时候,就修改它的物理地址. 静态重定位进程数据一旦确定位置,就不能再移动 动态重定位(动态运行时装入):作业装入内存的时候,不修改物理地址,直到运行的时候,根据重定位寄存器再修改地址. 对…...

uniapp刻度尺的实现(swiper)滑动打分器
实现图(百分制):滑动swiper进行打分,分数加减 <view class"scoring"><view class"toggle"><view class"score"><text>{{0}}</text><view class"scoreId&quo…...
cordova Xcode打包ios以及发布流程(ionic3适用)
第一步 1、申请iOS证书 2、导入证书到钥匙串 第二步 1、xcode配置iOS证书 1.1用Xcode打开你的项目(我的Xcode版本是新版) 修改如下图 回到基本信息设置界面,Bundie 这项填写,最先创建的那个appid,跟创建iOS描述文件时选…...
,新旧版idea打开同一个项目会不会出现不兼容)
idea中的.idea文件夹以及*.iml文件(新版idea没有*.iml文件了),新旧版idea打开同一个项目会不会出现不兼容
一、背景 我们有可能会在同一台电脑上安装2个 intellj idea。比如一个community edition一个ultimate edition(一个安装板一个绿色解压版) 当然了,两个idea之间可能版本号也会有差。 这篇文章就来讨论两个问题,一是关于idea产生…...

高性能网络编程 - The C10K problem 以及 网络编程技术角度的解决思路
文章目录 C10KC10K的由来C10K问题在技术层面的典型体现C10K问题的本质C10K解决思路思路一:每个进程/线程处理一个连接思路二:每个进程/线程同时处理多个连接(IO多路复用)● 实现方式1:直接循环处理多个连接● 实现方式…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...
