SpringMVC对请求参数的处理
如何获取SpringMVC中请求中的信息 ? 默认情况下,可以直接在方法的参数中填写跟请求参数一样的名称,此时会默认接受参 数 ,如果有值,直接赋值,如果没有,那么直接给空值 。
@Controller
@RequestMapping("/params")
public class ParamsController {@RequestMapping("/param01")public String param01(String username){System.out.println(username);return "index";}}接下来访问: http://localhost:8080/springmvc/param01?username=test
对应方法参数中的username值为test
如果请求的参数跟处理方法的参数名不一致呢?
使用 @RequestParam 管理请求参数
如果用了这个注解之后,默认必须要传入值,如果不传入值则报400(参数类型不匹配)错误,
如果不用这个注解,如果没有传入会自动传入null
value 用来重命名参数
required 用来指定参数是否必须传入值
true 默认 必须要传入, 如果没有传入则会报错:
HTTP Status 400 - Required String parameter 'username' is not present
false 可以不用必须传入值 ,如果没有传入会自动传入null
注意:不要用基础数据类型,因为基础数据类型无法接收null(会报500错)
defaultValue 默认值,当参数为null的时候会自动设置一个默认值
注意:当设置了默认值可以省略required=false
@RequestMapping("/param01")public String param01(@RequestParam(value="name",required = true) String username){System.out.println(username);return "index";}接下来可以访问: http://localhost:8080/springmvc/param01?name=test
相关文章:

SpringMVC对请求参数的处理
如何获取SpringMVC中请求中的信息 ? 默认情况下,可以直接在方法的参数中填写跟请求参数一样的名称,此时会默认接受参 数 ,如果有值,直接赋值,如果没有,那么直接给空值 。Controller RequestMapp…...

12年老外贸的经验分享
回想这12年的经历,很庆幸自己的三观一直是正确的,就是买家第一不管什么原因,只要你想退货,我都可以接受退款。不能退给上级供应商,我就自己留着,就是为了避免因为这个拒收而失去买家。不管是什么质量原因&a…...
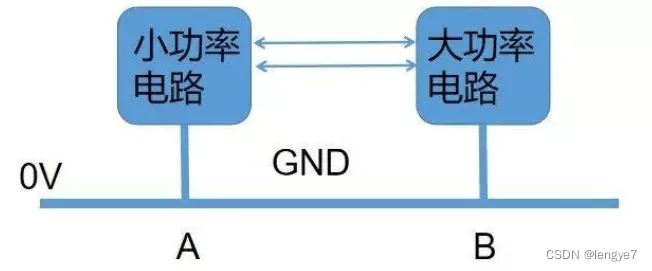
电子电路中的各种接地(接地保护与GND)
前言多年以前,雷雨天气下,建筑会遭遇雷击,从而破坏建筑以及伤害建筑内的人,为了避免雷击的伤害,人们发明了避雷针,并将避雷针接地线,从而引导雷击产生的电流经过地线流入到地下。地线࿱…...

php实现农历公历日期的相互转换
农历(Lunar calendar)和公历(Gregorian calendar)是两种不同的日历系统。公历是基于太阳和地球的运动来计算时间的,而农历是基于月亮的运动来计算时间的。农历中的月份是根据月亮的相对位置来确定的,而公历…...
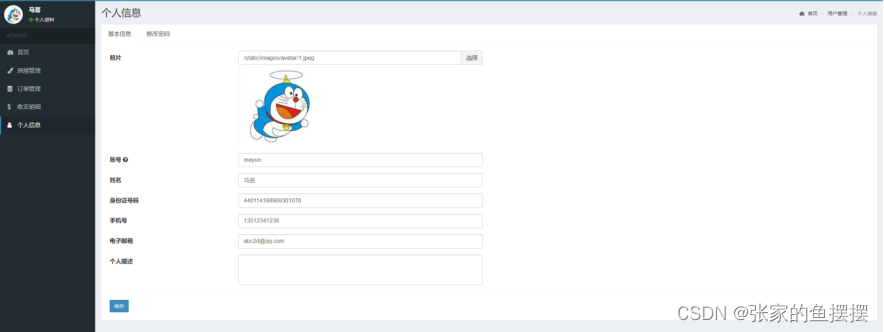
基于SpringBoot的房屋租赁管理系统的设计与实现
基于SpringBoot的房屋租赁管理系统的设计与实现 1 绪论 1.1 课题来源 随着社会的不断发展以及大家生活水平的提高,越来越多的年轻人选择在大城市发展。在大城市发展就意味着要在外面有一处安身的地方。在租房的过程中,大家也面临着各种各样的问题&…...

一文带你为PySide6编译MySQL插件驱动
1.概述 最近使用PySide6开发程序,涉及与MySQL的数据交互。但是qt官方自pyqt5.12(记不太清了)以后不再提供MySQL的插件驱动,只能自己根据qt的源码编译。不过网上大部分都是qt5的MySQL驱动的编译教程。后来搜到了一个qt6的编译教程…...
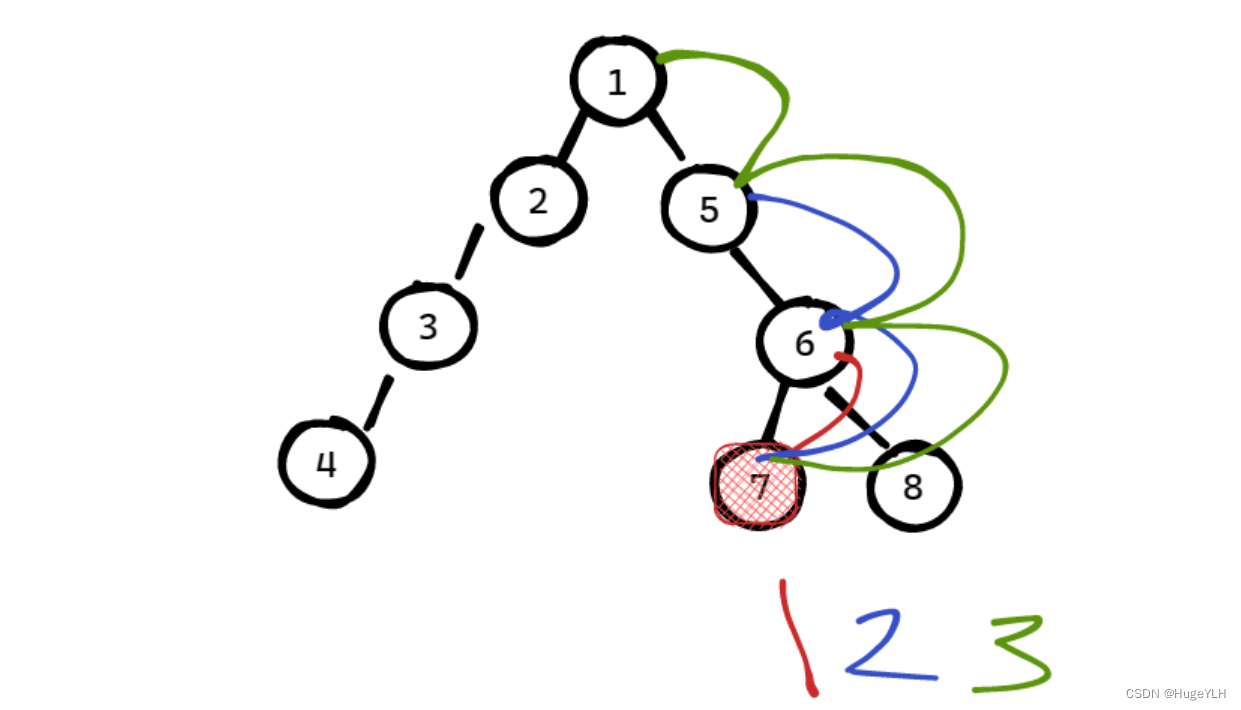
图论算法:树上倍增法解决LCA问题
文章目录树上倍增法: LCA问题树上倍增法: LCA问题 树上倍增法用于求解LCA问题是一种非常有效的方法。 倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k 可以发现倍增是呈 2的指数型递增的一类数据,和二分一样&…...
 和 execute()方法有什么区别)
Java线程池中submit() 和 execute()方法有什么区别
点个关注,必回关 文章目录一. execute和submit的区别与联系1、测试代码的整体框架如下:2、首先研究Future<?> submit(Runnable task)和void execute(Runnable command),3、submit(Runnable task, T result) 方法可以使submit执行完Run…...

Vue.extend和VueComponent的关系源码解析
目录 0.概念解释 前言 需求分析 Vue.extend 编程式的使用组件 源码分析 0.概念解释 Vue.extend和VueComponent是Vuejs框架中创建组件的两种不同方式。Vue.extend方法能够让你根据Vue对象(继承)来定义一个新的可重用的组件构造器。而VueComponent方…...
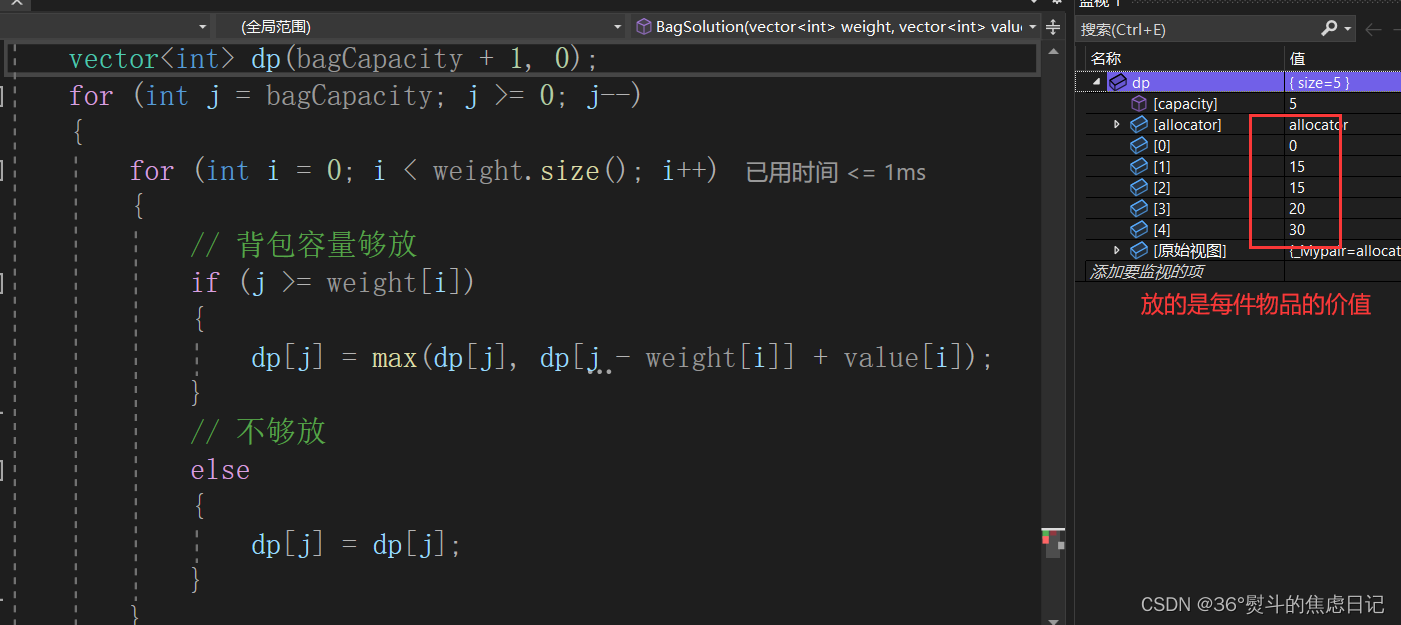
【动态规划】01背包问题(滚动数组 + 手画图解)
01背包除了可以用形象的二维动态数组表示外,还可以使用空间复杂度更低的一维滚动数组。 目录 文章目录 前言 一、滚动数组的基本理解 二、确定dp及其下标含义 三、确定递推公式 四、确定初始化 五、确定遍历顺序 1.用物品(正序)遍历背…...

javaEE 初阶 — 超时重传机制
文章目录超时重传机制1. 数据重复传输问题2. 如何解决数据重复传输问题3. 重传次数问题TCP 的工作机制:确认应答机制 超时重传机制 如果传输数据的时候丢包了该怎么办? 利用 超时重传,也就是超过了一定的时间,如果还没响应就重新…...

小米5x wlan无法打开解决
诱因:想要利用空置设备做节点服务器或者边缘计算,因此解锁并刷了magisk,印象中在刷之前wlan已经无法打开无法进行wifi联网 表现: 1 WLAN开关无法打开,或者虚假打开,无法扫描wifi 2 设置->我的设备->全…...

负载均衡之最小活跃数算法
文章目录[toc]一、概念二、场景与设计思路三、实现四、代码下载一、概念 活跃数 集群中各实例未处理的请求数。 最小活跃数 集群中各个实例,哪个实例未处理的请求数据最小,就称之为最小活跃数。 二、场景与设计思路 场景 以获取微服务地址为场景。 设计…...
JavaScript 评测代码运行速度的几种方法
一、使用 performance.now() API 在 JavaScript 中,可以使用 performance.now() API 来评测代码的运行速度。该 API 返回当前页面的高精度时间戳,您可以在代码执行前后调用它来计算代码执行所需的时间。 例如: let t0 performance.now();…...

Linux 编译器 gcc/g++
本文已收录至《Linux知识与编程》专栏! 作者:ARMCSKGT 演示环境:CentOS 7 目录 前言 正文 gcc/g常用命令 自定义可执行程序名命令-o 预处理指令-E 编译指令-S 汇编指令-c 链接指令gcc 命令巧记口诀 链接库 动态库-动态链接 静态库…...
2.Java基础【Java面试第三季】
2.Java基础【Java面试第三季】前言推荐2.Java基础01_字符串常量Java内部加载-上58同城的java字符串常量池面试code讲解intern()方法---源码解释02_字符串常量Java内部加载-下whyOpenJDK8底层源码说明递推步骤总结考查点03_闲聊力扣算法第一题字节跳动两数求和题目说明面试题解法…...
Java高级-多线程
本篇讲解java多线程 基本概念: 程序、进程、线程 **程序(program)**是为完成特定任务、用某种语言编写的一组指令的集合。即指一段静态的代码,静态对象。 **进程(process)**是程序的一次执行过程,或是正在运行的一个程序。是一个动态的过程…...

mysql高级(事务、存储引擎、索引、锁、sql优化、MVCC)
文章目录1.事务1.1 四大特性ACID1.2 并发事务2.存储引擎2.1 InnoDB2.2 MyISAM2.3 Memory2.4 存储引擎特点2.5 存储引擎的选择3.性能分析3.1 查看执行频次3.2 慢查询日志3.3 profile3.4 explain4.索引4.1 索引结构B-TreeBTreeHash面试题4.2 索引分类思考题4.3 语法4.4 使用规则最…...
Java后端开发功能模块思路
文章目录前言一、查找接口及参数信息1.1 找访问路径1.2 参数及返回结果信息1.3 编写功能模块函数二、代码设计思路三、总结前言 对于正在学习Java后端开发的同学来说,对于Java后端功能模块的开发过程及思路要有一个整体清晰的流程。才能保证在开发过程中更加的顺畅…...
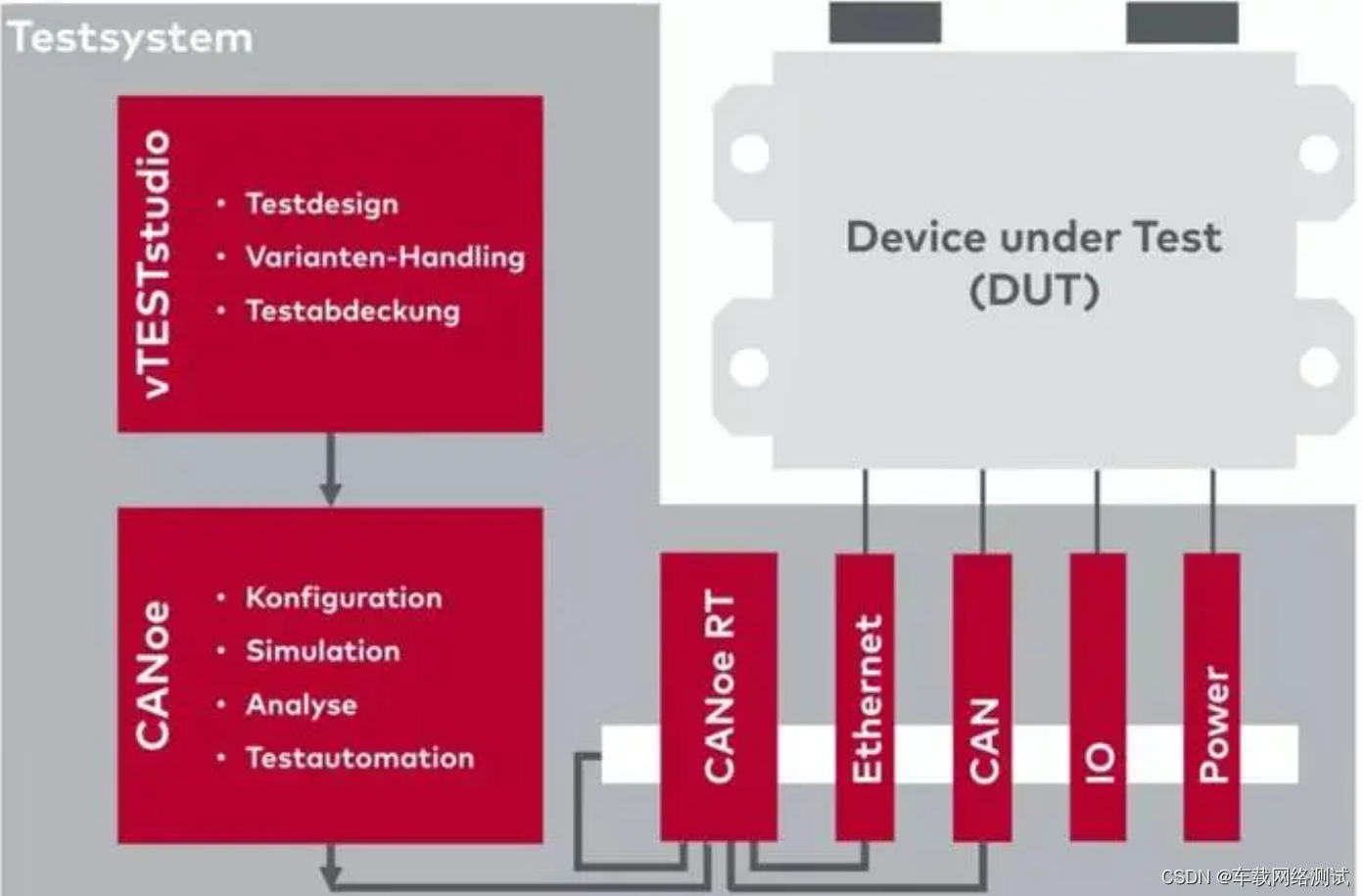
CAPL(vTESTStudio) - DoIP - TCP发送_05
TCP发送 参数定义 版本号:02 FD or 01 FE or 其他任意值数据类型:00 05 or 00 06 or 80 01 or其他任意值数据长度:想要发送的任意长度...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
