图论算法:树上倍增法解决LCA问题
文章目录
- 树上倍增法: LCA问题
树上倍增法: LCA问题
树上倍增法用于求解LCA问题是一种非常有效的方法。
倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k
可以发现倍增是呈 2的指数型递增的一类数据,和二分一样,二分是缩小范围的,而倍增是扩大的,因此倍增与二分都具有 logn的时间复杂度,对于求解某些问题是非常高效的。
什么是树的公共祖先?
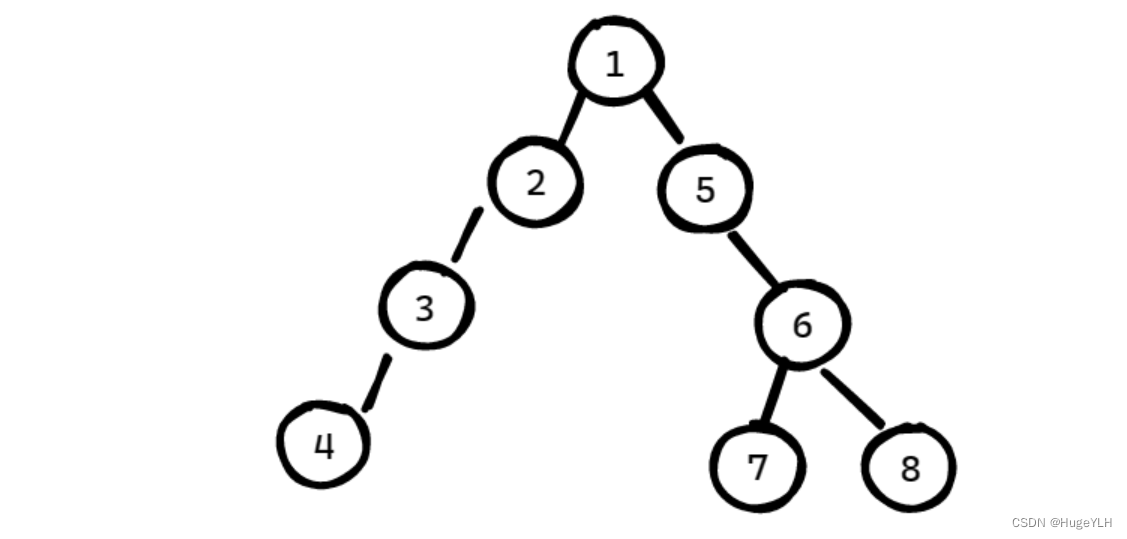
如图所示:
- 节点 7与 节点8的最近公共祖先是 节点6
- 节点3 与 节点5的最近公共祖先是节点1
类似这种问题我们可以使用 树上倍增法来实现
树上倍增的实现:
首先定义 fa[i] [j] 表示 节点编号为 i 的节点,向根节点方向走了 2^j 步所到达的节点
- 什么是走了 2^j 步??
走一条边规定为走了一步,j可以表示为 0 ,1,2 ,分别代表走了 1步,2步,4步
走了一步: 到达了节点6
走了两步: 到达了节点5
走了四步:超过了范围,因此只能到达 节点1
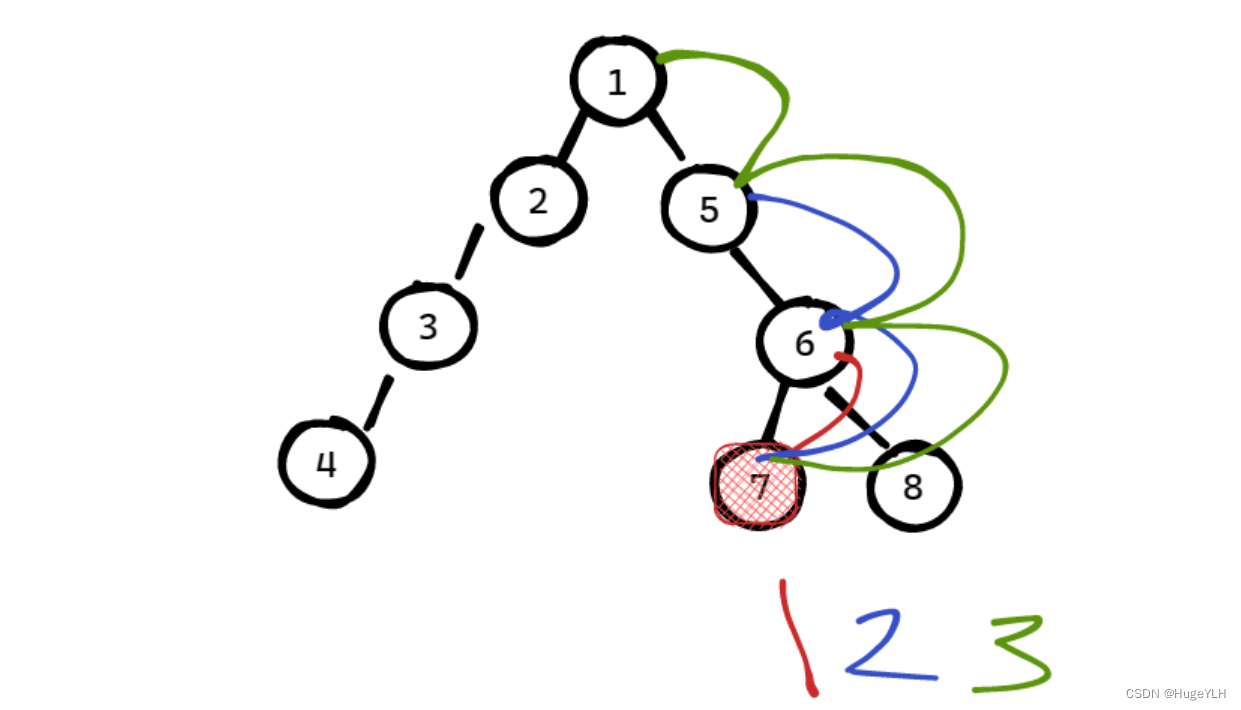
因此我们的 fa数组实际上记录的就是 节点 i 的 第 2^j 个祖先,分别为1:节点6;2:节点5,4:节点1
因此首先把整个树结构存储起来(使用链式前向星)
然后首先对整个图进行预处理
- 预处理的目标:
就是把每个 节点的 第 2^j 个的祖先找出来,用于之后的处理,同时我们还需要记录每个节点的深度,我们采用递归的形式,每次递归,节点的深度都是父节点的深度+1
注意:lg数组预处理每个节点的当前深度+1,可以使得某些地方得到优化
void init(int now,int father)
{fa[now][0]=father;//第now节点的第2^0个父亲节点,即第一个父亲节点是fatherdepth[now]=depth[father]+1;//now的深度是父亲节点深度+1//for (int i=1;i<=lg[depth[now]];i++)for (int i=1;(1<<i)<=depth[now];i++){fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组}//递归预处理当前点的所有子节点for (int i=head[now];i;i=edge[i].next){if (edge[i].to!=father){init(edge[i].to,now);}}
}
寻找LCA的过程:
我们会发现几个问题:
- 两个节点的深度不一样,该如何寻找呢?
- 什么时候寻找结束呢? 即什么时候才能找到他们的LCA 呢
首先来看第一个问题:
深度不同怎么解决? x和y节点
- 我们可以假设 x 节点的深度是最大的。
- 每次让x节点往上移动,直到x节点与y节点到达同一深度
什么时候结束寻找? 即找到了最近公共祖先?
- 当他们位于同一深度的时候,让他们两个节点一起出发,一起往上移动,直到不能再往上移动了为止,他们到达了一个相同的位置,这个节点就是最近公共祖先的节点,返回它即可。
int LCA(int x,int y)
{if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度while (depth[x]>depth[y])//让x与y到达同一深度,倍增x的深度{x=fa[x][lg[depth[x]-depth[y]]-1];}if (x==y) return x;//当他们相同时,LCA就是他们for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数,x与y同时倍增,直到xy到达同一位置{if (fa[x][k]!=fa[y][k]){x=fa[x][k];y=fa[y][k];}}return fa[x][0];//xy到达同一位置,返回父节点
}
模板例题:
最近公共祖先
完整AC code
//TODO: Write code here
int n,m,s;
const int N=1e6+10;
int nums[N];
struct Edge
{int to,w,next;
}edge[N];
int head[N],cnt;
int fa[N][50],depth[N],lg[N];
void add_edge(int u,int v)
{edge[++cnt].next=head[u];edge[cnt].to=v;head[u]=cnt;
}
void init(int now,int father)
{fa[now][0]=father;//第now节点的第2^0个父亲节点,即第一个父亲节点是fatherdepth[now]=depth[father]+1;//now的深度是父亲节点深度+1for (int i=1;i<=lg[depth[now]];i++){fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组}//递归预处理当前点的所有子节点for (int i=head[now];i;i=edge[i].next){if (edge[i].to!=father){init(edge[i].to,now);}}
}
int LCA(int x,int y)
{if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度while (depth[x]>depth[y])//让x与y到达同一深度,倍增x的深度{x=fa[x][lg[depth[x]-depth[y]]-1];}if (x==y) return x;//当他们相同时,LCA就是他们for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数,x与y同时倍增,直到xy到达同一位置{if (fa[x][k]!=fa[y][k]){x=fa[x][k];y=fa[y][k];}}return fa[x][0];//xy到达同一位置,返回父节点
}
signed main()
{cin>>n>>m>>s;for (int i=1;i<=n-1;i++){int u,v;scanf("%lld%lld",&u,&v);add_edge(u,v);add_edge(v,u);}for (int i=1;i<=n;i++){lg[i]=lg[i-1]+(1<<lg[i-1]==i);}init(s,0);for (int i=1;i<=m;i++){int u,v;scanf("%lld%lld",&u,&v);printf("%lld\n",LCA(u,v));}
#define one 1return 0;
}
<<lg[i-1]==i);
}
init(s,0);
for (int i=1;i<=m;i++)
{
int u,v;
scanf(“%lld%lld”,&u,&v);
printf(“%lld\n”,LCA(u,v));
}
#define one 1
return 0;
}
参考:[树上倍增法](https://blog.csdn.net/chengqiuming/article/details/126694822)
相关文章:

图论算法:树上倍增法解决LCA问题
文章目录树上倍增法: LCA问题树上倍增法: LCA问题 树上倍增法用于求解LCA问题是一种非常有效的方法。 倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k 可以发现倍增是呈 2的指数型递增的一类数据,和二分一样&…...
 和 execute()方法有什么区别)
Java线程池中submit() 和 execute()方法有什么区别
点个关注,必回关 文章目录一. execute和submit的区别与联系1、测试代码的整体框架如下:2、首先研究Future<?> submit(Runnable task)和void execute(Runnable command),3、submit(Runnable task, T result) 方法可以使submit执行完Run…...

Vue.extend和VueComponent的关系源码解析
目录 0.概念解释 前言 需求分析 Vue.extend 编程式的使用组件 源码分析 0.概念解释 Vue.extend和VueComponent是Vuejs框架中创建组件的两种不同方式。Vue.extend方法能够让你根据Vue对象(继承)来定义一个新的可重用的组件构造器。而VueComponent方…...
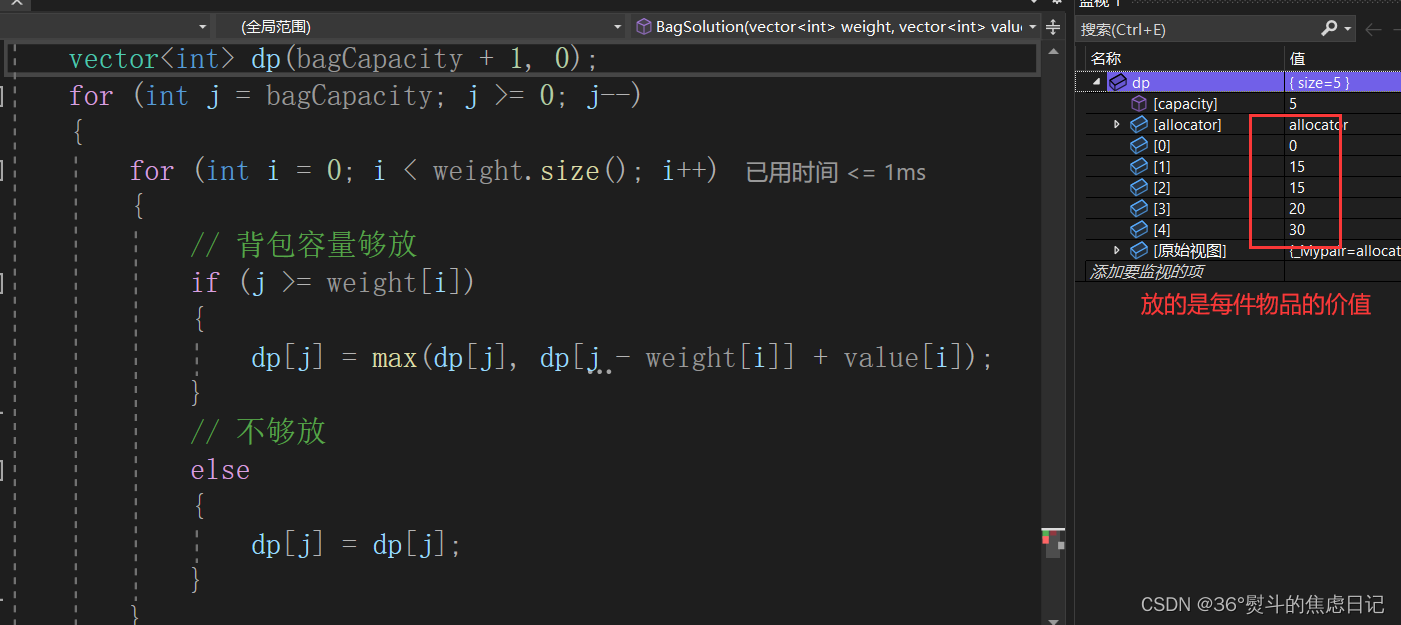
【动态规划】01背包问题(滚动数组 + 手画图解)
01背包除了可以用形象的二维动态数组表示外,还可以使用空间复杂度更低的一维滚动数组。 目录 文章目录 前言 一、滚动数组的基本理解 二、确定dp及其下标含义 三、确定递推公式 四、确定初始化 五、确定遍历顺序 1.用物品(正序)遍历背…...

javaEE 初阶 — 超时重传机制
文章目录超时重传机制1. 数据重复传输问题2. 如何解决数据重复传输问题3. 重传次数问题TCP 的工作机制:确认应答机制 超时重传机制 如果传输数据的时候丢包了该怎么办? 利用 超时重传,也就是超过了一定的时间,如果还没响应就重新…...

小米5x wlan无法打开解决
诱因:想要利用空置设备做节点服务器或者边缘计算,因此解锁并刷了magisk,印象中在刷之前wlan已经无法打开无法进行wifi联网 表现: 1 WLAN开关无法打开,或者虚假打开,无法扫描wifi 2 设置->我的设备->全…...

负载均衡之最小活跃数算法
文章目录[toc]一、概念二、场景与设计思路三、实现四、代码下载一、概念 活跃数 集群中各实例未处理的请求数。 最小活跃数 集群中各个实例,哪个实例未处理的请求数据最小,就称之为最小活跃数。 二、场景与设计思路 场景 以获取微服务地址为场景。 设计…...
JavaScript 评测代码运行速度的几种方法
一、使用 performance.now() API 在 JavaScript 中,可以使用 performance.now() API 来评测代码的运行速度。该 API 返回当前页面的高精度时间戳,您可以在代码执行前后调用它来计算代码执行所需的时间。 例如: let t0 performance.now();…...

Linux 编译器 gcc/g++
本文已收录至《Linux知识与编程》专栏! 作者:ARMCSKGT 演示环境:CentOS 7 目录 前言 正文 gcc/g常用命令 自定义可执行程序名命令-o 预处理指令-E 编译指令-S 汇编指令-c 链接指令gcc 命令巧记口诀 链接库 动态库-动态链接 静态库…...
2.Java基础【Java面试第三季】
2.Java基础【Java面试第三季】前言推荐2.Java基础01_字符串常量Java内部加载-上58同城的java字符串常量池面试code讲解intern()方法---源码解释02_字符串常量Java内部加载-下whyOpenJDK8底层源码说明递推步骤总结考查点03_闲聊力扣算法第一题字节跳动两数求和题目说明面试题解法…...
Java高级-多线程
本篇讲解java多线程 基本概念: 程序、进程、线程 **程序(program)**是为完成特定任务、用某种语言编写的一组指令的集合。即指一段静态的代码,静态对象。 **进程(process)**是程序的一次执行过程,或是正在运行的一个程序。是一个动态的过程…...

mysql高级(事务、存储引擎、索引、锁、sql优化、MVCC)
文章目录1.事务1.1 四大特性ACID1.2 并发事务2.存储引擎2.1 InnoDB2.2 MyISAM2.3 Memory2.4 存储引擎特点2.5 存储引擎的选择3.性能分析3.1 查看执行频次3.2 慢查询日志3.3 profile3.4 explain4.索引4.1 索引结构B-TreeBTreeHash面试题4.2 索引分类思考题4.3 语法4.4 使用规则最…...
Java后端开发功能模块思路
文章目录前言一、查找接口及参数信息1.1 找访问路径1.2 参数及返回结果信息1.3 编写功能模块函数二、代码设计思路三、总结前言 对于正在学习Java后端开发的同学来说,对于Java后端功能模块的开发过程及思路要有一个整体清晰的流程。才能保证在开发过程中更加的顺畅…...
CAPL(vTESTStudio) - DoIP - TCP发送_05
TCP发送 参数定义 版本号:02 FD or 01 FE or 其他任意值数据类型:00 05 or 00 06 or 80 01 or其他任意值数据长度:想要发送的任意长度...
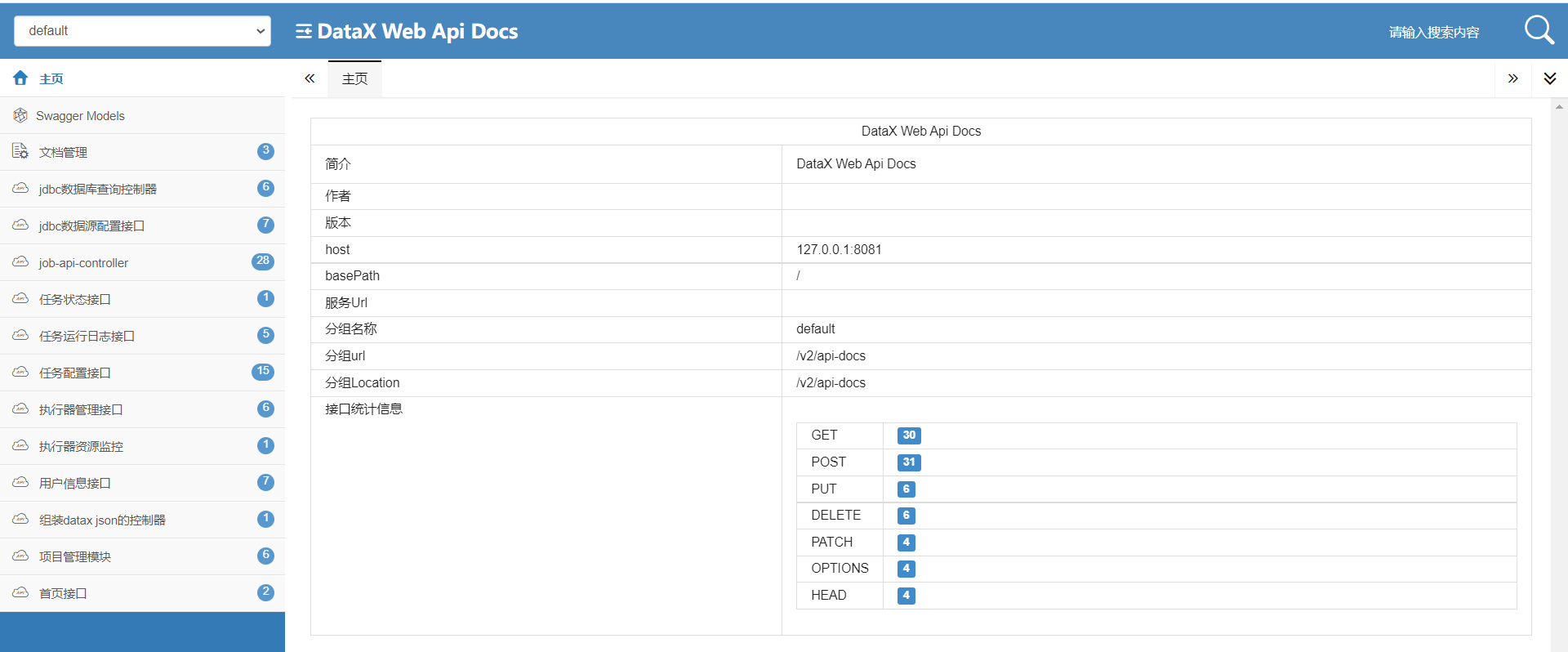
使用IntelliJ IDEA搭建datax-web开发环境
记录:372场景:使用IntelliJ IDEA搭建datax-web开发环境,以及datax-web基本使用。版本:JDK 1.8Python 2.7.5datax-web开源地址:https://github.com/WeiYe-Jing/datax-web1.配置Maven环境1.1安装目录目录:D:\…...

[SSD固态硬盘技术 14] GC垃圾回收太重要了
今天介绍臭名昭著的垃圾收集 过程(或“GC”),maybe 这是对JAVA 工程师而言。当遇到GC导致速度降低时候, 他们真的想跳脚。 我想到我的小孩打疫苗,哭的哇哇叫, 在他的眼里疫苗应该也是讨厌的吧, 但事实真的如此吗? 但首先,让我们考虑一下如果根本没有 GC,闪存系统会发…...
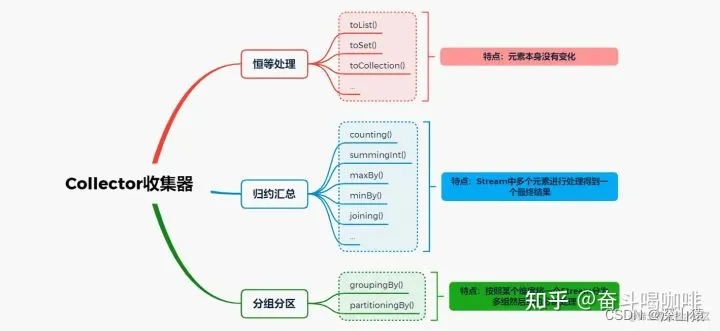
lamada表达式、stream、collect整理
lamada表达式格式 格式:( parameter-list ) -> { expression-or-statements } 实例:简化匿名内部类的写法 原本写法: public class LamadaTest { public static void main(String[] args) { new Thread(new Runnable() { …...
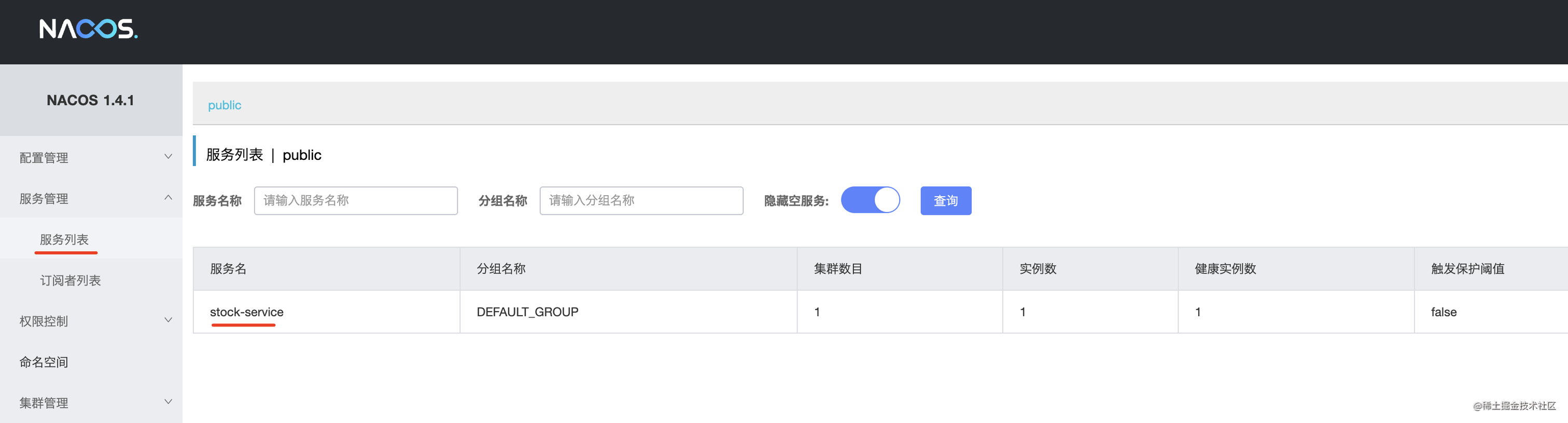
Nacos 入门微服务项目实战
Nacos 核心源码精讲 - IT贱男 - 掘金小册全方位源码精讲,深度剖析 Nacos 注册中心和配置中心的核心思想。「Nacos 核心源码精讲」由IT贱男撰写,375人购买https://s.juejin.cn/ds/BuC3Vs9/ Hi,大家好,欢迎大家来学习《Nacos 核心源…...
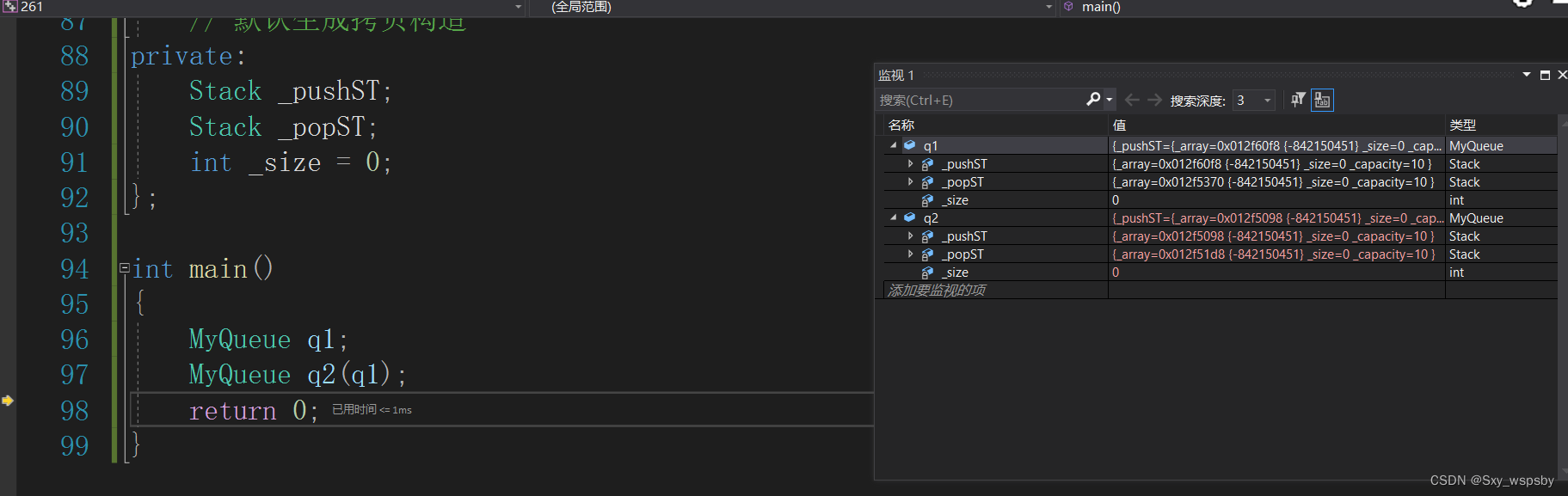
【c++】类和对象:让你明白“面向一个对象有多重要”:构造函数,析构函数,拷贝构造函数的深入学习
文章目录 什么是面向对象?一:类是什么? 1.类的访问限定符 2.封装 3.类的实例化 4.this指针二:类的6个默认成员函数 1.构造函数 2.析构函数 3.拷贝构造函数什么是面向对象? c语言是面向…...

职场IT老手教你3步教你玩转可视化大屏设计,让领导眼前一亮!
我是制造企业的IT中心的研发人员,平常工作就是配合业务部门出出报表,选型一些商业软件,并在内部负责实施运维。最近领导出去参观了一些数字化转型比较领先的工厂和制造企业,回来就甩给我几张图,问能不能我们也做几个这…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
