IS-LM模型:从失衡到均衡的模拟
IS-LM模型:从失衡到均衡的模拟
文章目录
- IS-LM模型:从失衡到均衡的模拟
- @[toc]
- 1 I S − L M 1 IS-LM 1IS−LM模型
- 2 数值模拟
- 2.1 长期均衡解
- 2.2 政府部门引入
- 2.3 价格水平影响
- 2.4 随机扰动因素
文章目录
- IS-LM模型:从失衡到均衡的模拟
- @[toc]
- 1 I S − L M 1 IS-LM 1IS−LM模型
- 2 数值模拟
- 2.1 长期均衡解
- 2.2 政府部门引入
- 2.3 价格水平影响
- 2.4 随机扰动因素
1 I S − L M 1 IS-LM 1IS−LM模型
I S − L M IS-LM IS−LM是产品市场和货币市场共同均衡时的模型,它由两条曲线构成,分别是 I S IS IS曲线和 L M LM LM曲线。其中 I S IS IS曲线是在产品市场均衡(产品服务供给等于需求、计划支出等于实际支出、计划投资等于储蓄、非计划存货等于0)条件下,均衡实际收入 Y Y Y与实际利率 r r r之间的反向变化关系; L M LM LM曲线是在货币市场均衡(货币供给等于货币需求)条件下,均衡实际利率 r r r与实际收入 Y Y Y之间的正向变化关系。用方程表示为
{ Y = C ( Y ) + I ( r ) L ( r , Y ) = M / P \left\{\begin{array}{l} Y=C(Y)+I(r)\\ L(r,Y)=M/P \end{array}\right. {Y=C(Y)+I(r)L(r,Y)=M/P
其中 Y = C ( Y ) + I ( r ) Y=C(Y)+I(r) Y=C(Y)+I(r)为产品市场均衡条件(计划支出=实际支出)。消费 C ( Y ) C(Y) C(Y)是关于收入 Y Y Y的函数,假设是线性的:
C ( Y ) = α + β Y C(Y)=\alpha+\beta Y C(Y)=α+βY
其中 β ∈ ( 0 , 1 ) \beta\in(0,1) β∈(0,1)称为边际消费倾向, α > 0 \alpha>0 α>0为自主消费,即没有收入时的消费。在资本边际效率不变时,投资 I ( r ) I(r) I(r)是关于利率 r r r的递减函数,假设也是线性的:
I ( r ) = e − d r I(r)=e-dr I(r)=e−dr
其中 e > 0 e>0 e>0是自发投资, d d d是投资对利率的敏感程度。于是产品市场均衡条件可记作
Y = α + β Y + e − d r Y=\alpha+\beta Y+e-dr Y=α+βY+e−dr
L ( r , Y ) L(r,Y) L(r,Y)为实际货币需求,它是由 L 1 ( Y ) L_1(Y) L1(Y)需求和 L 2 ( r ) L_2(r) L2(r)需求构成。 L 1 ( Y ) L_1(Y) L1(Y)由交易性需求和预防性需求构成,随收入 Y Y Y增加而增加,不妨假定为正比例函数
L 1 ( Y ) = k Y L_1(Y)=kY L1(Y)=kY
其中 k k k表示用于支付日常开支(交易性需求)和未来不确定性(预防性需求)占实际收入的比重。 L 2 ( r ) L_2(r) L2(r)需求称为投机性需求,它是关于实际利率的递减函数,假设为负比例函数:
L 2 ( r ) = A − h r L_2(r)=A-hr L2(r)=A−hr
其中 A > 0 A>0 A>0是参数, h h h表示 L 2 L_2 L2对利率 r r r变化的敏感程度。 M M M表示名义货币供给, P P P表示价格水平, M / P M/P M/P表示实际货币供给。货币市场均衡条件可以记作
k Y + A − h r = M / P kY+A-hr=M/P kY+A−hr=M/P
我们将上述两个模型重新写在一起
{ Y = α + β Y + e − d r k Y + A − h r = M / P \left\{\begin{array}{l} Y=\alpha+\beta Y+e-dr\\ kY+A-hr=M/P \end{array}\right. {Y=α+βY+e−drkY+A−hr=M/P
将 r , Y r,Y r,Y视为内生变量,两个方程组可以解出唯一均衡值,记作 ( r ∗ , Y ∗ ) (r^*,Y^*) (r∗,Y∗)。其中 r ∗ r^* r∗称为均衡实际利率, Y ∗ Y^* Y∗称为均衡实际收入,或均衡国民收入。从几何上看,也就是这两条直线的交点。
然而,初始的实际收入和实际利率并不是均衡的,很有可能并不在上述两条直线的交点处,例如下图 E ′ E' E′, E ′ ′ E'' E′′和 E ′ ′ ′ E''' E′′′。

假设初始状态在 E ′ ′ ′ E''' E′′′,此时计划投资大于储蓄 I > S I>S I>S,实际收入 Y Y Y增加,实际利率 r r r增加,即 E ′ ′ ′ E''' E′′′点即向右移动,又向上移动,合力为右上方,直至进入 I I II II区域。在 I I II II区域中, I < S I<S I<S,实际收入减少,于是向左移动; L > M L>M L>M,实际利率继续向上移动,合力为左上方,此时进入 I I I区域。在 I I I区域, Y Y Y减少, r r r降低,合力在左下方,进入 I V IV IV区域。在 I V IV IV区域, Y Y Y增加, r r r降低,进入 I I I III III区域,于是重新回到 I I I III III区域。但每次都与均衡点 E E E不断接近。
为了使上述模型动态化,引入时间因素 t t t,于是
{ C t = α + β Y t I t = e − d r t Y t + 1 = C t + I t k Y t + A − h r t + 1 = M / P \left\{\begin{array}{l} C_t = \alpha+\beta Y_t\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t\\ kY_t+A-hr_{t+1}=M/P \end{array}\right. ⎩ ⎨ ⎧Ct=α+βYtIt=e−drtYt+1=Ct+ItkYt+A−hrt+1=M/P
整理得到
{ C t = α + β Y t I t = e − d r t Y t + 1 = C t + I t r t + 1 = ( k Y t + A − M / P ) / h \left\{\begin{array}{l} C_t = \alpha+\beta Y_t\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t\\ r_{t+1} = (kY_t+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧Ct=α+βYtIt=e−drtYt+1=Ct+Itrt+1=(kYt+A−M/P)/h
在长期中,非均衡逐渐向均衡靠拢, r t ≈ r t + 1 ≈ r ∗ r_t\approx r_{t+1} \approx r^* rt≈rt+1≈r∗, Y t ≈ Y t + 1 ≈ Y ∗ Y_t\approx Y_{t+1}\approx Y^* Yt≈Yt+1≈Y∗,于是
{ C ∗ = α + β Y ∗ I ∗ = e − d r ∗ Y ∗ = C ∗ + I ∗ r ∗ = ( k Y ∗ + A − M / P ) / h \left\{\begin{array}{l} C^* = \alpha+\beta Y^*\\ I^*=e-dr^*\\ Y^*= C^*+I^*\\ r^* = (kY^*+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧C∗=α+βY∗I∗=e−dr∗Y∗=C∗+I∗r∗=(kY∗+A−M/P)/h
使用行列式求解得到长期均衡点为
{ r ∗ = k ( α + e ) + ( 1 − β ) ( A − M / P ) k d + h ( 1 − β ) Y ∗ = h ( α + e ) − d ( A − M / P ) k d + h ( 1 − β ) \left\{\begin{array}{l} r^* = \dfrac{k(\alpha+e)+(1-\beta)(A-M/P)}{kd+h(1-\beta)} \\ Y^* = \dfrac{h(\alpha+e)-d(A-M/P)}{kd+h(1-\beta)} \\ \end{array}\right. ⎩ ⎨ ⎧r∗=kd+h(1−β)k(α+e)+(1−β)(A−M/P)Y∗=kd+h(1−β)h(α+e)−d(A−M/P)
2 数值模拟
2.1 长期均衡解
令参数 α = 500 \alpha=500 α=500, β = 0.5 \beta=0.5 β=0.5, e = 1250 e=1250 e=1250, d = 250 d=250 d=250, k = 0.5 k=0.5 k=0.5, h = 250 h=250 h=250, A = 1000 A=1000 A=1000, M = 1250 M=1250 M=1250, P = 1 P=1 P=1,代入上述均衡解得到
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
r_star = (k*(alpha+e)+(1-beta)*(A-M/P))/(k*d+h*(1-beta))
Y_star =( h*(alpha+e)-d*(A-M/P))/(k*d+h*(1-beta))
r_star
Y_star
# 3
# 2000
现在假设初始实际利率为 r 0 = 10 r_0=10 r0=10, Y 0 = 5000 Y_0=5000 Y0=5000,基于下列公式
{ C t = α + β Y t I t = e − d r t Y t + 1 = C t + I t r t + 1 = ( k Y t + A − M / P ) / h \left\{\begin{array}{l} C_t = \alpha+\beta Y_t\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t\\ r_{t+1} = (kY_t+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧Ct=α+βYtIt=e−drtYt+1=Ct+Itrt+1=(kYt+A−M/P)/h
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
T = 100 # 迭代次数r = numeric()
Y = numeric()
# 初始值
r[1] = 10
Y[1] = 5000
# 迭代
for (t in 1:T) {C = 500+0.5*Y[t]I = 1250-250*r[t]Y[t+1] = C+Ir[t+1] = (k*Y[t]+A-M/P)/h}
par(mfrow=c(1,2),mar = c(5,5,5,5))
plot(Y,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际利率均衡过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
plot(r,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际收入均衡过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")par(mfrow=c(1,1))
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "均衡点收敛过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")


2.2 政府部门引入
引入政府部门,政府决策变量包括政府支出 G G G、税收 T T T和转移支付 T r T_r Tr,此时均衡条件如下:
{ C t = α + β ( Y t − T + T r ) I t = e − d r t Y t + 1 = C t + I t + G r t + 1 = ( k Y t + A − M / P ) / h \left\{\begin{array}{l} C_t = \alpha+\beta (Y_t-T+T_r)\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t +G\\ r_{t+1} = (kY_t+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧Ct=α+β(Yt−T+Tr)It=e−drtYt+1=Ct+It+Grt+1=(kYt+A−M/P)/h
令政府购买 G = 500 G=500 G=500,税收 T = 20 T=20 T=20,转移支付 T r = 5 T_r=5 Tr=5,
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
T = 20
Tr = 5
G = 500T = 100 # 迭代次数r = numeric()
Y = numeric()
# 初始值
r[1] = 10
Y[1] = 5000
# 迭代
for (t in 1:T) {C = 500+0.5*(Y[t]-T+Tr)I = 1250-250*r[t]Y[t+1] = C+I+Gr[t+1] = (k*Y[t]+A-M/P)/h}
par(mfrow=c(1,2),mar = c(5,5,5,5))
plot(Y,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际利率均衡过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
plot(r,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际收入均衡过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")par(mfrow=c(1,1))
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "均衡点收敛过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")


2.3 价格水平影响
使价格水平 P P P不断下降,实际货币供给不断增加,实际货币供给增加又导致均衡实际利率不断降低,进而导致投资不断增加,均衡国民收入不断增加。
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
T = 20
Tr = 5
G = 500
T = 100 # 迭代次数
r = numeric()
Y = numeric()
# 初始值
r[1] = 10
Y[1] = 5000
# 迭代P = c(1,0.8,0.6,0.4)
par(mfrow=c(2,2),mar = c(5,5,5,5))
for(j in P){for (t in 1:T) {C = 500+0.5*(Y[t]-T+Tr)I = 1250-250*r[t]Y[t+1] = C+I+Gr[t+1] = (k*Y[t]+A-M/j)/h}plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = paste("价格水平P=",j),cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")grid(col = "black")
}

2.4 随机扰动因素
除收入外,还有其他一些因素也会影响消费;同理,除了利率,也有其他因素也会影响投资大小;货币需求和货币供给之间也存在随机误差。因此,均衡条件进一步改进为
{ C t = α + β ( Y t − T + T r ) + ε t I t = e − d r t + v t Y t + 1 = C t + I t + G r t + 1 = ( k Y t + A − M / P + w t ) / h ε t , v t , w t ∼ N ( 0 , 1 ) \left\{\begin{array}{l} C_t = \alpha+\beta (Y_t-T+T_r)+\varepsilon_t \\ I_t=e-dr_t+v_t\\ Y_{t+1}= C_t+I_t +G\\ r_{t+1} = (kY_t+A-M/P+w_t)/h\\ \varepsilon_t,v_t,w_t\sim N(0,1) \end{array}\right. ⎩ ⎨ ⎧Ct=α+β(Yt−T+Tr)+εtIt=e−drt+vtYt+1=Ct+It+Grt+1=(kYt+A−M/P+wt)/hεt,vt,wt∼N(0,1)
其中 ε t , v t , w t \varepsilon_t,v_t,w_t εt,vt,wt假定服从标准正态分布。
#------------------------随机扰动影响-----------------------------
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
T = 20
Tr = 5
G = 500
T = 100 # 迭代次数
r = numeric()
Y = numeric()
# 初始值
r[1] = 4
Y[1] = 2450
# 迭代
for (t in 1:T) {C = 500+0.5*(Y[t]-T+Tr)+rnorm(1,0,1)I = 1250-250*r[t]+rnorm(1,0,1)Y[t+1] = C+I+Gr[t+1] = (k*Y[t]+A-M/P+rnorm(1,0,1) )/h}
par(mfrow=c(1,2),mar = c(5,5,5,5))
plot(Y,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际利率均衡过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
plot(r,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际收入均衡过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")par(mfrow=c(1,1))
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "均衡点收敛过程",cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")


相关文章:

IS-LM模型:从失衡到均衡的模拟
IS-LM模型:从失衡到均衡的模拟 文章目录 IS-LM模型:从失衡到均衡的模拟[toc] 1 I S − L M 1 IS-LM 1IS−LM模型2 数值模拟2.1 长期均衡解2.2 政府部门引入2.3 价格水平影响2.4 随机扰动因素 1 I S − L M 1 IS-LM 1IS−LM模型 I S − L M IS-LM IS−LM是…...
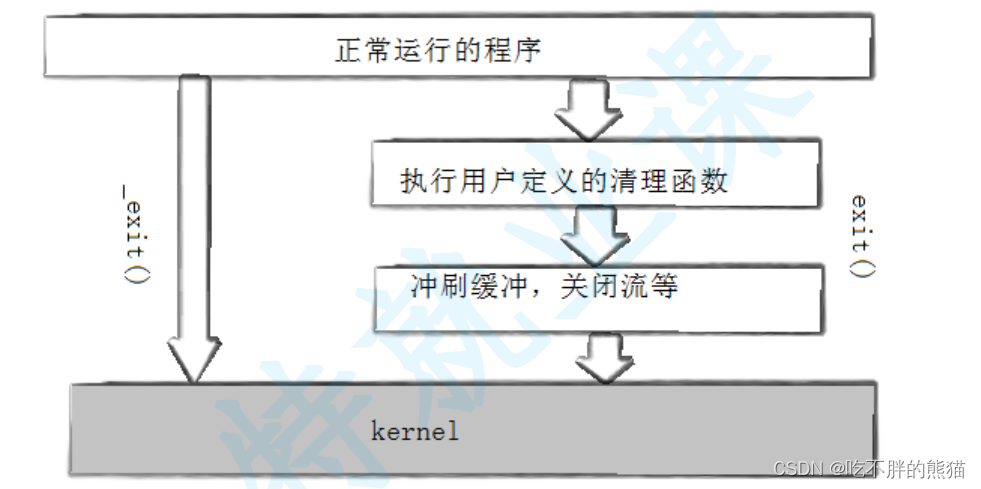
【Linux】进程终止
进程退出场景 代码运行完毕,结果正确代码运行完毕,结果不正确代码异常终止 可以用return 的不同的返回值数字,表征不同的出错原因退出码,所以进程运行正不正常我们可以查看退出码来判断; 如果进程异常,退…...

55.跳跃游戏
题目描述:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示…...
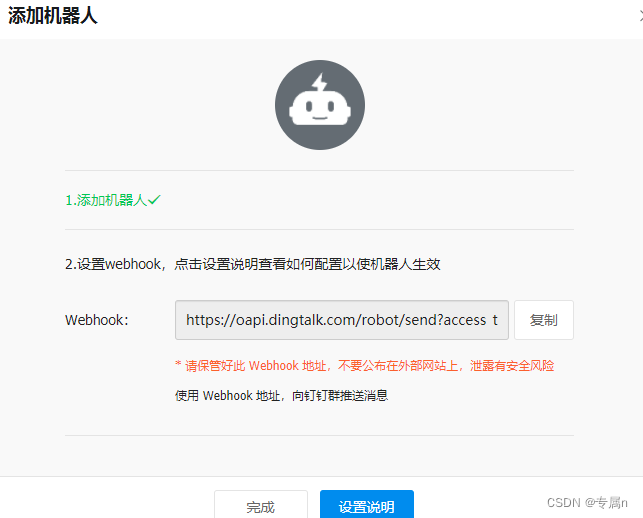
php实现钉钉机器人推送消息和图片内容(完整版)
先来看下实现效果: 代码如下: function send_dingtalk_markdown($webhook , $title , $message "", $atMobiles [], $atUserIds []) {$data ["msgtype" > "markdown","markdown" > ["title" > $title,&quo…...

A Survey on Neural Network Interpretability
A Survey on Neural Network Interpretability----《神经网络可解释性调查》 摘要 随着深度神经网络的巨大成功,人们也越来越担心它们的黑盒性质。可解释性问题影响了人们对深度学习系统的信任。它还与许多伦理问题有关,例如算法歧视。此外,…...

代码随想录 Day41 动态规划09 LeetCode T121 买卖股票的最佳时机 T122 买卖股票的最佳时机II
前言 这两题看起来是不是有点眼熟,其实我们在贪心章节就已经写过了这两道题,当时我们用的是将利润分解,使得我们始终得到的是最大利润 假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。 相当于(prices[3] - prices[2]) (pri…...
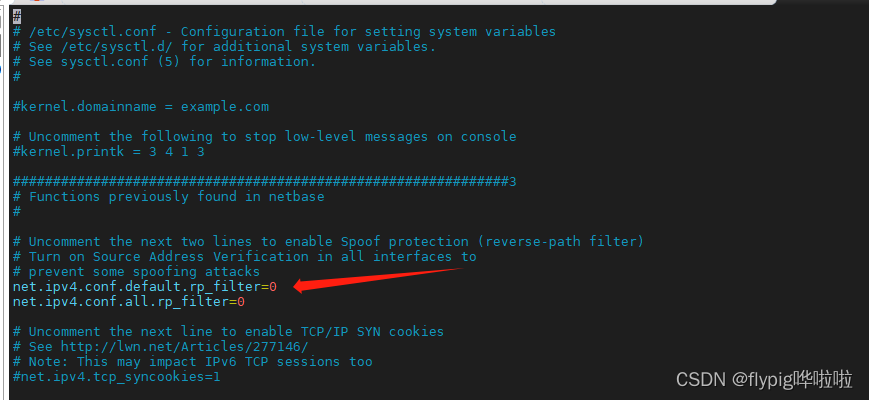
ubuntu18-recvfrom接收不到广播报文异常分析
目录 前言 一、UDP广播接收程序 二、异常原因分析 总结 前言 在ubuntu18.04系统中,编写udp接收程序发现接收不到广播报文,使用抓包工具tcpdump可以抓取到广播报文,在此对该现象分析解析如下文所示。 一、UDP广播接收程序 UDP广播接收程序如…...

漏刻有时百度地图API实战开发(6)多个标注覆盖层级导致不能响应点击的问题
漏刻有时百度地图API实战开发(1)华为手机无法使用addEventListener click 的兼容解决方案漏刻有时百度地图API实战开发(2)文本标签显示和隐藏的切换开关漏刻有时百度地图API实战开发(3)自动获取地图多边形中心点坐标漏刻有时百度地图API实战开发(4)显示指定区域在移动端异常的解…...
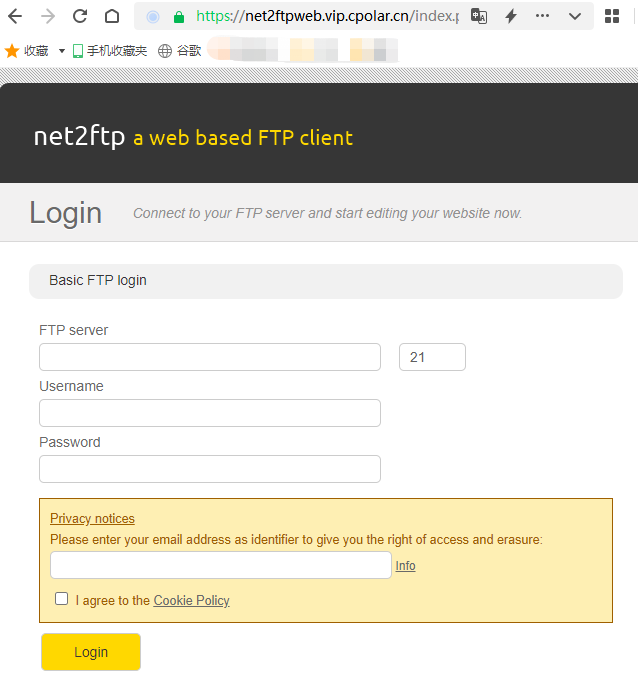
使用Net2FTP轻松打造免费的Web文件管理器并公网远程访问
文章目录 1.前言2. Net2FTP网站搭建2.1. Net2FTP下载和安装2.2. Net2FTP网页测试 3. cpolar内网穿透3.1.Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 文件传输可以说是互联网最主要的应用之一,特别是智能设备的大面积使用,无论是个人…...

MySQL的表格去重,史上最简便的算法,一看就会
首先,表格my_tab02存在很多重复的数据: #表格的去重 方法一: 详细内容传送门:表格的去重 -- 思路: -- 1.先创建一张临时表 my_tmp,该表的结构和my_tab02一样 -- 2.把my_tmp的记录通过distinct关键字 处理后 把记录复…...

this是指向的哪个全局变量,改变this指向的方法有几种?
在JavaScript中,this关键字指向当前执行上下文中的对象。它的具体指向取决于函数的调用方式。 改变this指向的方法有四种: 1.使用call()方法:call()方法在调用函数时将指定的对象作为参数传递进去,从而改变函数的this指向。用法示…...

电脑msvcp110.dll丢失怎么办,msvcp110.dll缺失的详细修复步骤
在现代科技发展的时代,电脑已经成为我们生活和工作中不可或缺的工具。然而,由于各种原因,电脑可能会出现一些问题,其中之一就是msvcp110.dll文件丢失。这个问题可能会导致一些应用程序无法正常运行,给我们的生活和工作…...
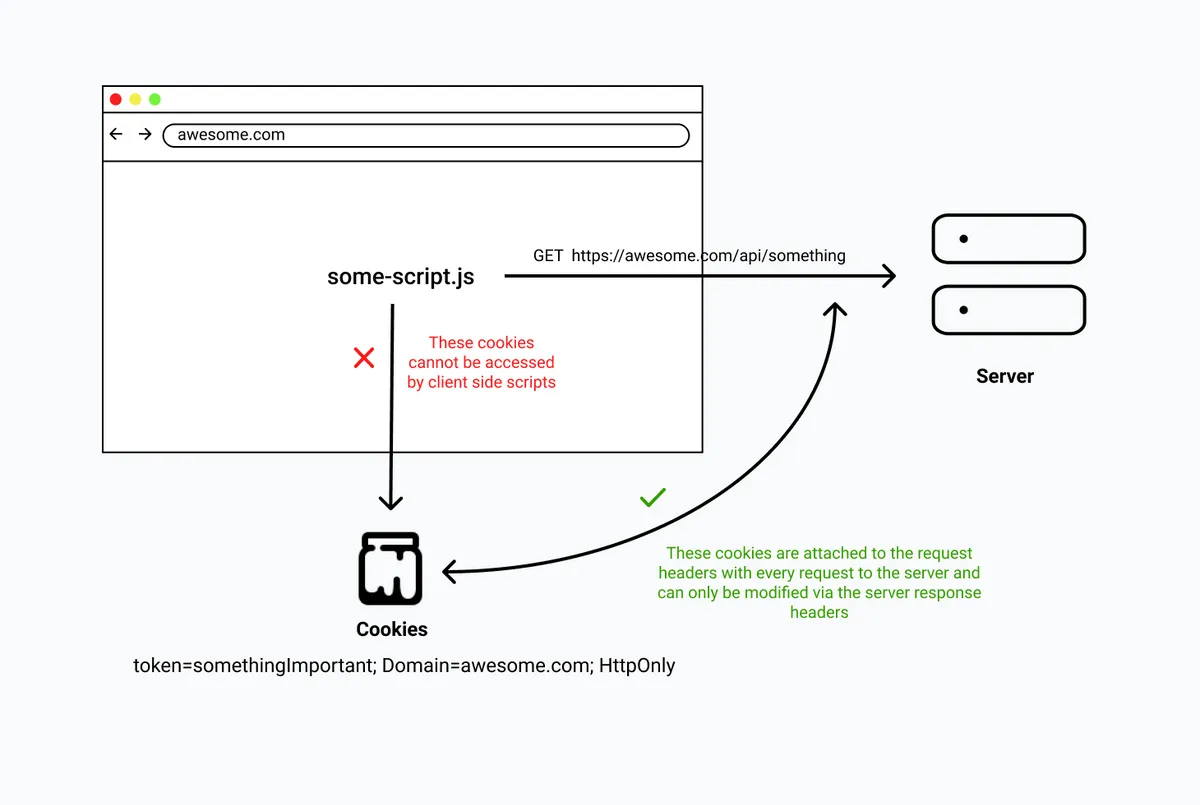
cookie 里面都包含什么属性?
结论先行: Cookie 中除了名称和值外,还有几个比较常见的,例如: Domain 域:指定了 cookie 可以发送到哪些域,只有发送到指定域或其子域的请求才会携带该cookie; Path 路径:指定哪些…...

LinuxMySql
结构化查询语言 DDL(数据定义语言) 删除数据库drop database DbName; 创建数据库create database DbName; 使用数据库use DbName; 查看创建数据库语句以及字符编码show create database 43th; 修改数据库属性(字符编码改为gbk)…...
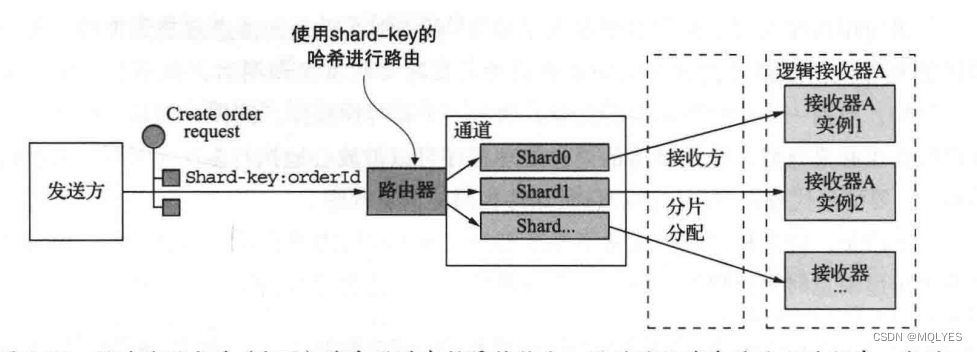
《微服务架构设计模式》之三:微服务架构中的进程通信
概述 交互方式 客户端和服务端交互方式可以从两个维度来分: 维度1:一对一和多对多 一对一:每个客户端请求由一个实例来处理。 一对多:每个客户端请求由多个实例来处理。维度2:同步和异步 同步模式:客户端…...

μC/OS-II---内核:任务调度
目录 内核:调度(oc_core.c文件的函数)OS_TCB(任务控制块)初始化任务控制块列表(ucos_ii.h文件的函数)系统调用,主动让渡CPU发生中断,强制当前任务让渡CPU就绪表(ucos_ii.h文件的函数)设置任务进…...

小程序发成绩
在这个数字化快速发展的时代,让学生能够方便快捷地获取自己的成绩已经成为一项基本的需求。那么,如何实现这一目标呢?对于许多老师来说,可能首先想到的是使用各种代码或者Excel来发布成绩查询。今天,我们就来探讨一下这…...

tensorflow内存泄漏或模型只加载不运行
使用tf2模型进行推理的过程中,发现模型的内存占用在逐步增加,甚至会因为OOM被kill掉进程,有时候模型只加载不运行,搜索得到很多五花八门的答案,有些认为是tf2本身的问题,但在使用内存追踪的时候发现&#x…...

npm和yarn的一些命令
文章目录 前言 前言 提示:生命并不短暂,短暂的是人。 --阿多尼斯 yarn config set registry https://registry.npmjs.org --globalnpm install -g cnpm --registryhttps://registry.npm.taobao.org # 切换淘宝源: yarn config set registry…...

Linux开发工具之自动化构建工具-make/Makefile
文章目录 1.make/Makefile的介绍2.简单编写及使用3.ACM时间4.extern的复习5.多文件的编译5.0复习翻译过程5.1多文件的构成5.2手动编译5.3利用Makefile 1.make/Makefile的介绍 make是一个命令 makefile是一个文件[makefile也对] 之前的学习都没有维护项目结构 当有多个.c文件 先…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
