【代码随想录】算法训练营 第十六天 第六章 二叉树 Part 3
104. 二叉树的最大深度
题目
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例:
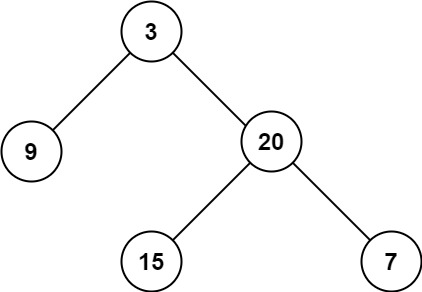
输入:root = [3,9,20,null,null,15,7] 输出:3
思路
用递归来做,其中心思路是,一个结点的最大深度相当于其左右子树的最大深度加一,这就可以利用递归求得子树深度了。
接下来是递归三部曲:
1. 首先确定返回值和参数,返回值肯定是深度,参数则是二叉树结点;
2. 其次确定递归终止条件,也就是当结点为空时返回0;
3. 最后明确每一次递归要做的事,其实就是按找中心思路返回最大深度。
代码
class Solution {
public:int getdepth(TreeNode* node) {if (node == NULL) return 0;int leftdepth = getdepth(node->left);int rightdepth = getdepth(node->right);int depth = 1 + max(leftdepth, rightdepth);return depth;}int maxDepth(TreeNode* root) {return getdepth(root);}
};111. 二叉树的最小深度
题目
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
思路
这道题的中心思路跟上面的一样,都是用递归法,每次取左右子树最小深度加一,不过这里有一个易错点,那就是深度要从叶子结点开始算,所以当遇到一个只有一个子树的结点时,不能记录空的一边,而是递归返回有子树的那边的深度。
代码
class Solution {
public:int getdepth(TreeNode* node) {if (node == NULL) return 0;int leftdepth = getdepth(node->left);int rightdepth = getdepth(node->right);if (node->left == NULL && node->right != NULL)return 1 + rightdepth;if (node->left != NULL && node->right == NULL)return 1 + leftdepth;int depth = 1 + min(leftdepth, rightdepth);return depth;}int minDepth(TreeNode* root) {return getdepth(root); }
};222. 完全二叉树的结点个数
题目
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
普通解法
管他完不完全,反正也是二叉树,既然是二叉树,之前学过的递归和非递归遍历都可以用来求结点数,只需要把原来的结点值入vector变成计数器加一,下面是用非递归前序遍历来做的:
class Solution {
public:int countNodes(TreeNode* root) {stack<TreeNode*> st;int num = 0;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* cur = st.top();st.pop();num++;if (cur->right) st.push(cur->right);if (cur->left) st.push(cur->left);}return num;}
};完全二叉树解法
完全二叉树可以不断拆分为一个满二叉树和一个完全二叉树,每一个满二叉树可以一边往下走一边求深度,如果左右子树的深度相同,就可以直接计算出这个二叉树的结点个数,因为满二叉树的结点数等于2的深度次方减一,如果不是满二叉树,就递归求解这个完全二叉树的根节点的左右子树的结点数再加一。
class Solution {
public:int countNodes(TreeNode* root) {if (root == NULL) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 0, rightDepth = 0;while (left) {left = left->left;leftDepth++;}while (right) {right = right->right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1;}return countNodes(root->left) + countNodes(root->right) + 1;}
};相关文章:

【代码随想录】算法训练营 第十六天 第六章 二叉树 Part 3
104. 二叉树的最大深度 题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例: 输入:root [3,9,20,null,null,15,7] 输出:3 思路 用递归来做,…...

【C++数据结构】顺序存储结构的抽象实现
文章目录 前言一、目标二、SeqList实现要点三、SeqList函数实现3.1 get函数3.2 set函数3.3 insert函数带2个参数的insert带一个参数的insert 3.4 remove函数3.5 clear函数3.6 下标运算符重载函数无const版本const版本 3.7 length函数 总结 前言 当谈到C数据结构时,…...

LeetCode75——Day31
文章目录 一、题目二、题解 一、题目 206. Reverse Linked List Given the head of a singly linked list, reverse the list, and return the reversed list. Example 1: Input: head [1,2,3,4,5] Output: [5,4,3,2,1] Example 2: Input: head [1,2] Output: [2,1] Exa…...
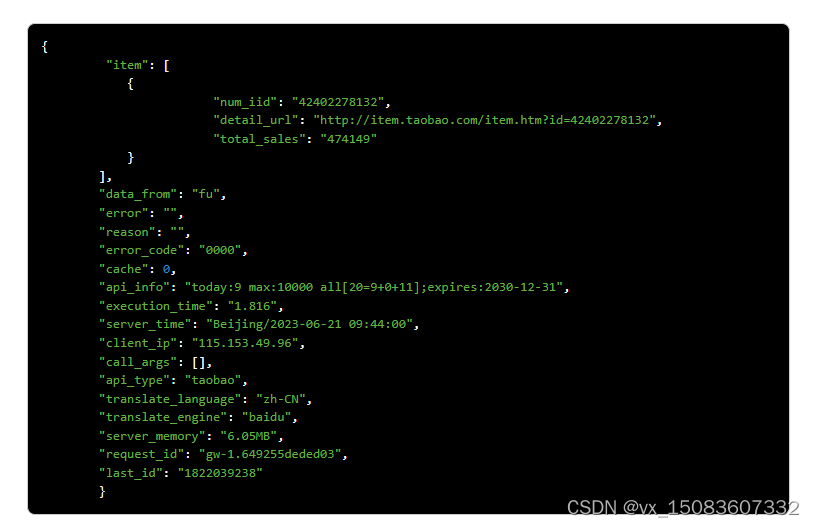
小白学爬虫:通过商品ID或商品链接封装接口获取淘宝商品销量数据接口|淘宝商品销量接口|淘宝月销量接口|淘宝总销量接口
淘宝商品销量接口是淘宝开放平台提供的一种API接口,通过该接口,商家可以获取到淘宝平台上的商品销量数据。使用淘宝商品销量接口的步骤如下: 1、在淘宝开放平台注册并创建应用,获取API Key和Secret Key等必要的信息。 2、根据淘宝…...

AI:75-基于生成对抗网络的虚拟现实场景增强
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...
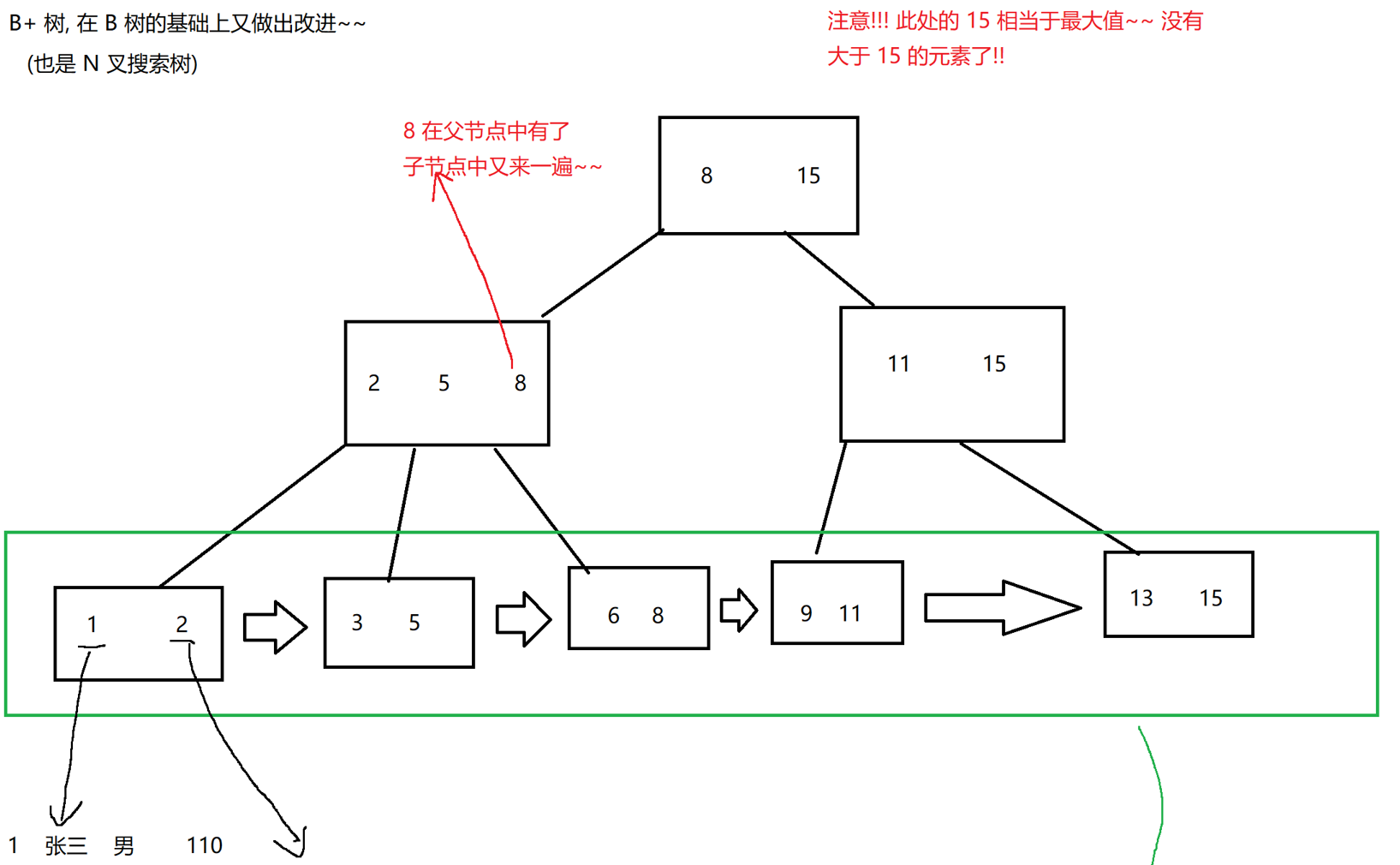
【MySQL数据库】| 索引以及背后的数据结构
🎗️ 主页:小夜时雨 🎗️ 专栏:MySQL数据库 🎗️ 如何优雅的活着,是我找寻的方向 目录 1. 基本知识2. 索引背后的数据结构总结 1. 基本知识 概念 索引是一种特殊的文件,包含着对数据表里所有…...
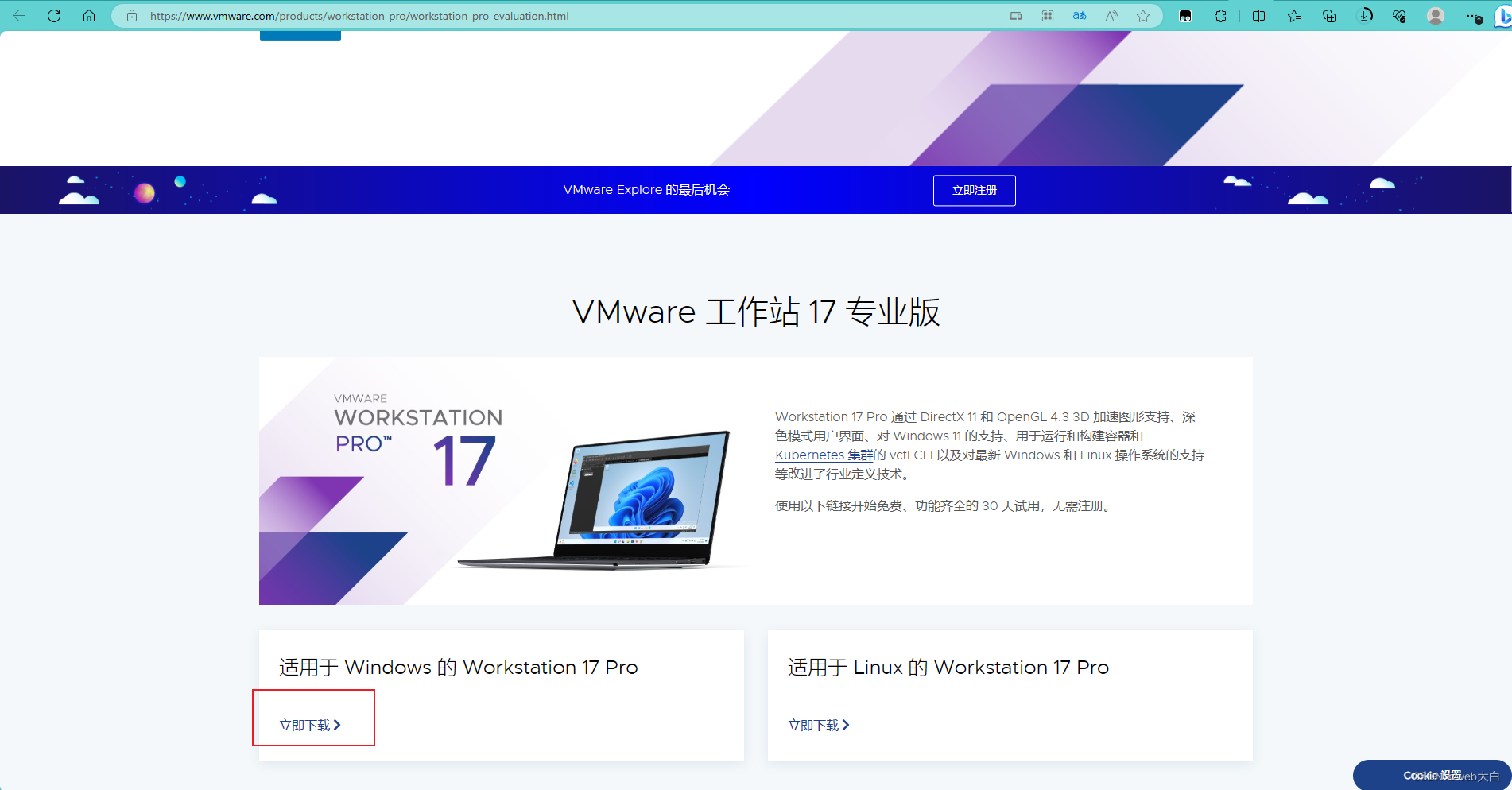
家用电脑做服务器,本地服务器搭建,公网IP申请,路由器改桥接模式,拨号上网
先浇一盆冷水! 我不知道其他运营商是什么情况。联通的运营商公网IP端口 80、8080、443 都会被屏蔽掉,想要开放必须企业备案(个人不行)才可以。也就是说,只能通过其他端口进行showtime了。 需要哪些东西? 申…...

原神游戏干货分享:探索璃月的宝箱秘密,提高游戏资源获取效率!
《原神》是一款备受玩家喜爱的开放世界冒险游戏,而在游戏中获取资源是提升角色实力的重要途径。在这篇实用干货分享中,我们将介绍一些探索璃月地区的宝箱秘密,帮助你提高游戏资源获取的效率。 首先,璃月地区的宝箱分为普通宝箱和精…...
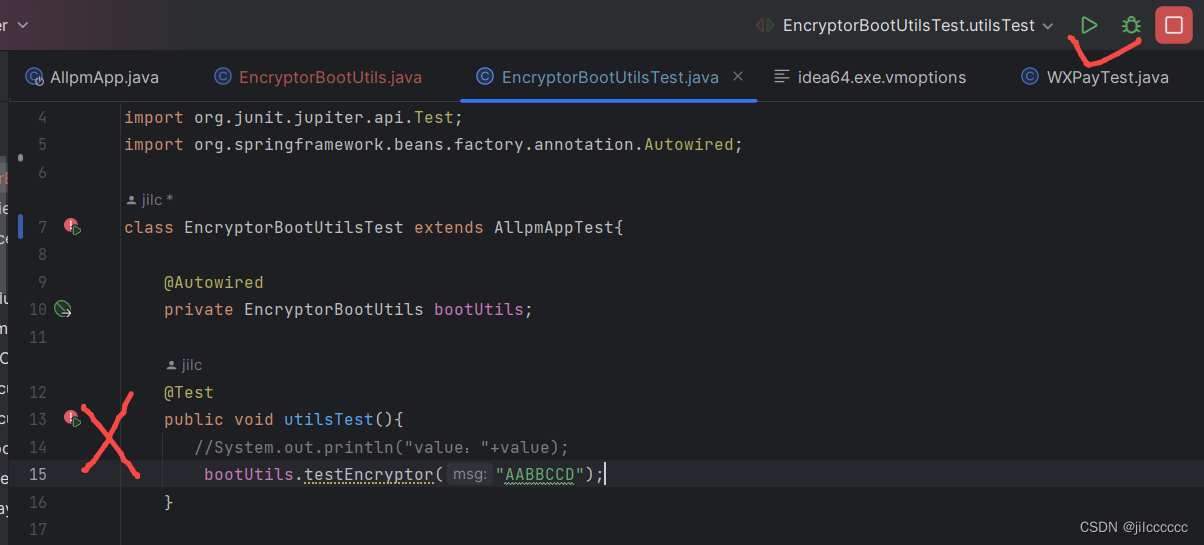
idea 2023 设置启动参数、单元测试启动参数
找到上方的editconfigration, 如下图,如果想在启动类上加,就选择springboot,如果想在单元测试加,就选择junit 在参数栏设置参数,多个参数以空格隔开 如果没有这一栏,就选择就可以了。 然后&…...
)
RSA加密算法(后端)
public class RSA {private static final String RSA_ALGORITHM "RSA";/*** 生成RSA密钥对** return RSA密钥对*/public static KeyPair generateKeyPair() throws NoSuchAlgorithmException {KeyPairGenerator keyPairGenerator KeyPairGenerator.getInstance(RSA…...
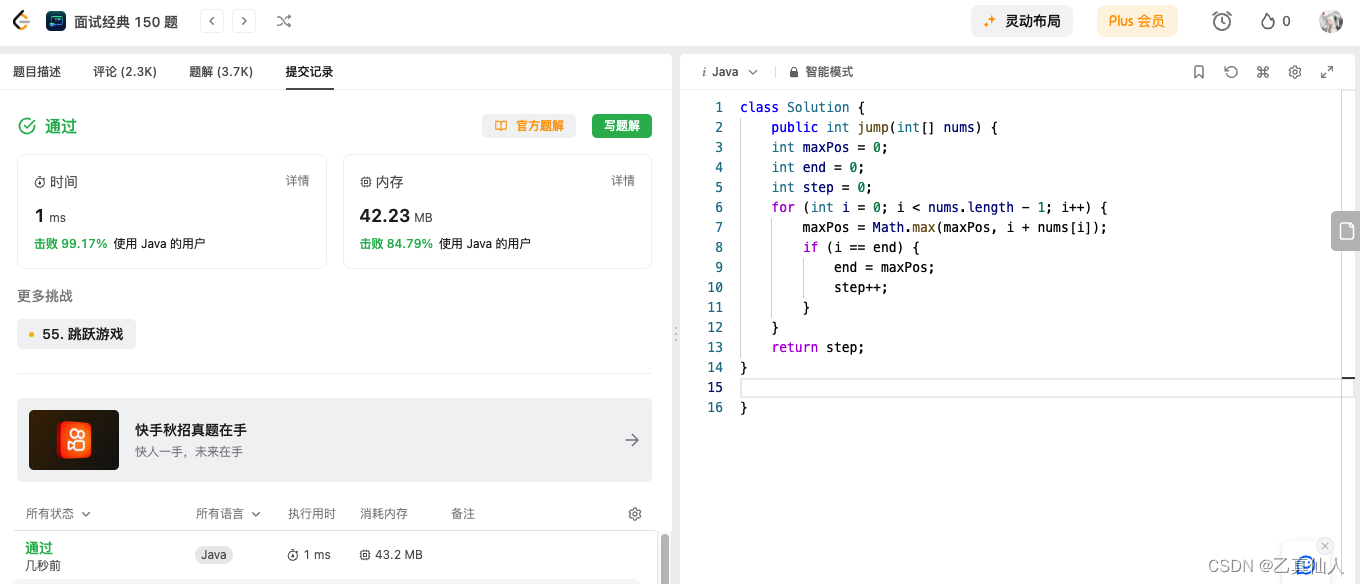
挑战100天 AI In LeetCode Day08(热题+面试经典150题)
挑战100天 AI In LeetCode Day08(热题面试经典150题) 一、LeetCode介绍二、LeetCode 热题 HOT 100-102.1 题目2.2 题解 三、面试经典 150 题-103.1 题目3.2 题解 一、LeetCode介绍 LeetCode是一个在线编程网站,提供各种算法和数据结构的题目&…...
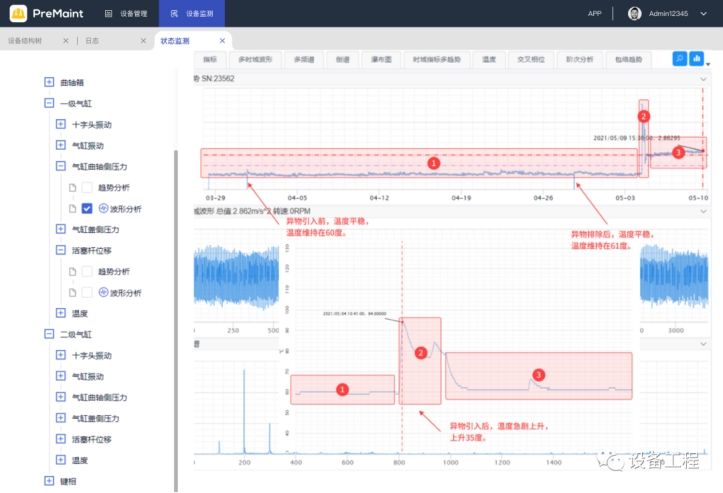
地铁机电设备健康管理现状及改善方法
轨道交通和我们的生活息息相关,从火车到地铁再到轻轨,给人们的出行带来了很大的便利。因此,保障轨道交通的的正常运行和安全至关重要,需要运维人员及时排查设备的问题,解决故障,保证轨道交通的安全运行。本…...

安卓NDK开发
1、jni:java native interface 作用:用于java代码和C、c代码的交互(代码混编); 分类使用:Jni静态注册、jni动态注册 2、静态注册 1).绑定java方法和C/C方法的方式之一; …...
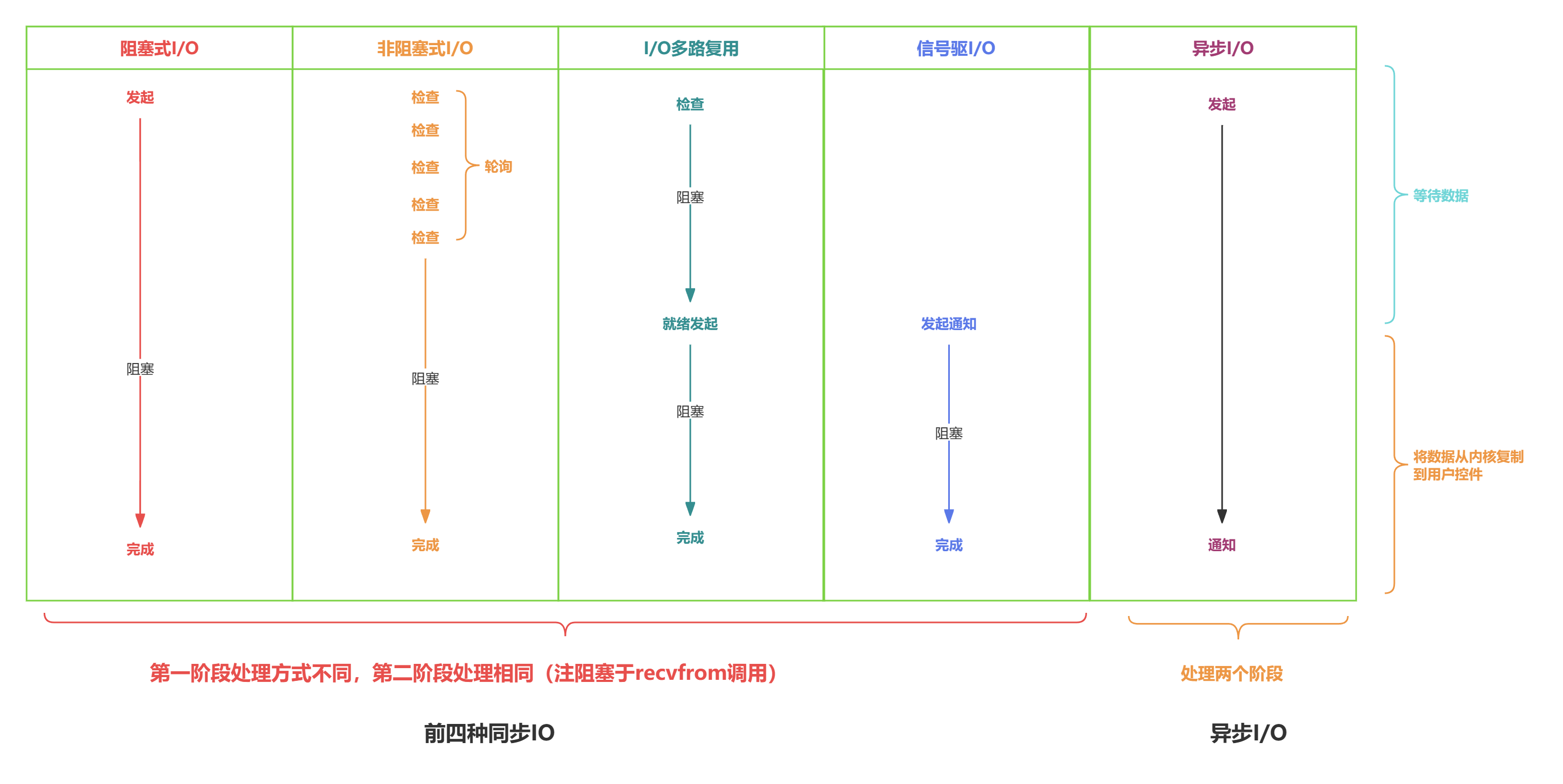
高性能网络编程 - 解读5种I/O模型
文章目录 服务端处理网络请求流程图基础概念阻塞调用 vs 非阻塞调用同步处理 vs 异步处理阻塞、非阻塞 和 同步、异步的区别recvfrom 函数 五种I/O模型I/O模型1:阻塞式 I/O 模型(blocking I/O)I/O模型2:非阻塞式 I/O 模型(non-blocking I/O&a…...

复盘一个诡异的Bug
该Bug的诡异之处在于这是一个由多种因素综合碰撞之后形成的综合体。纵观整个排查过程,一度被错误的目标误导,花费大量功夫后才找到问题点所在,成熟的组件在没有确凿证据之前不能随意怀疑其稳定性。 前言 此前在接入两台粒径谱仪(…...
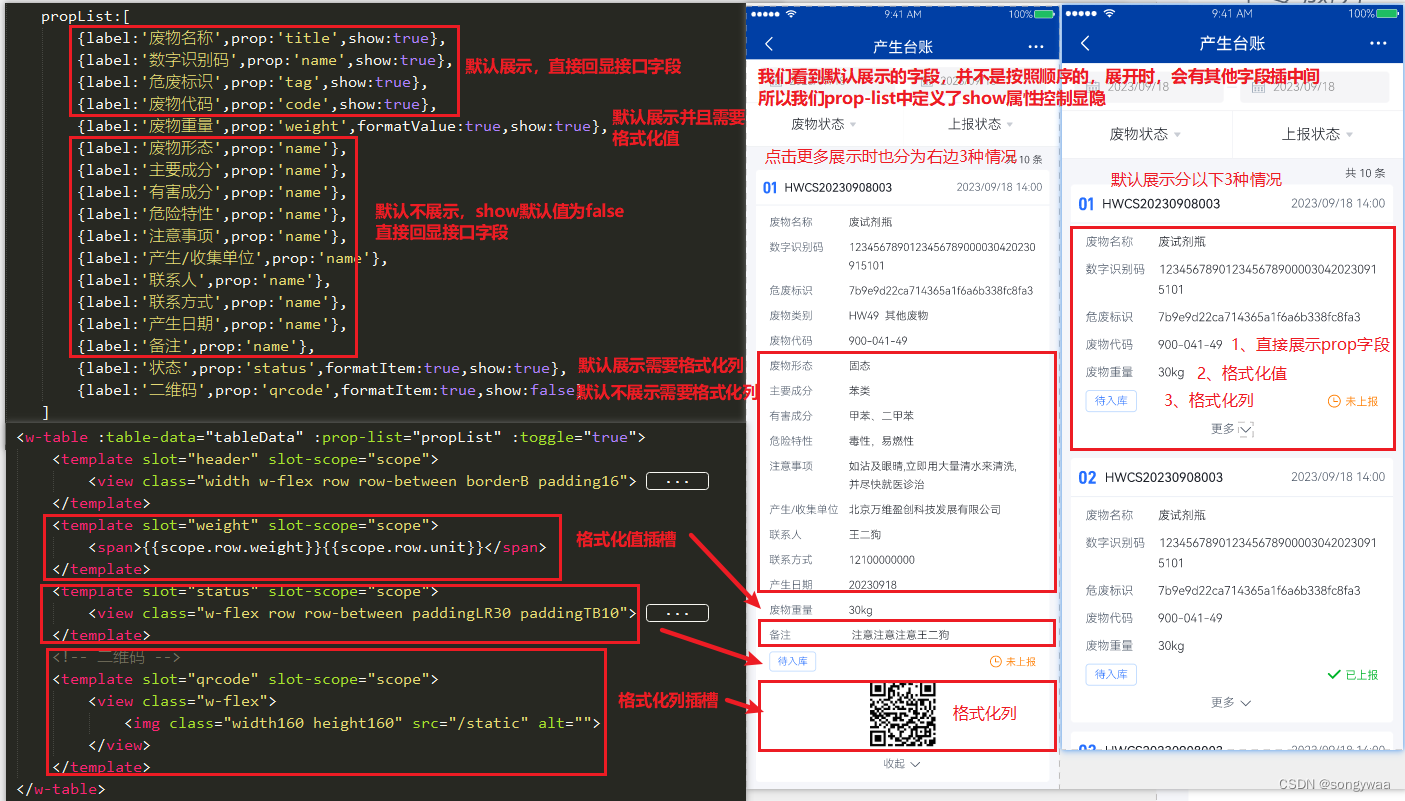
【uniapp】通用列表封装组件
uniapp页面一般都会有像以下的列表页面,封装通用组件,提高开发效率; (基于uView前端框架) 首先,通过设计图来分析一下页面展示和数据结构定义 w-table组件参数说明 参数说明类型可选值默认值toggle列表是…...
17 Linux 中断
一、Linux 中断简介 1. Linux 中断 API 函数 ① 中断号 每个中断都有一个中断号,通过中断号可以区分出不同的中断。在 Linux 内核中使用一个 int 变量表示中断号。 ② request_irq 函数 在 Linux 中想要使用某个中断是需要申请的,request_irq 函数就是…...
微信小程序真机调试连接状态一直在正常和未链接之间反复横跳?
背景:小程序真机调试的时候,发现真机的network不显示接口调用情况,控制台也没有输出内容。具体如下所示; 解决方法: 1、确保手机端连接的网络和微信开发者工具网络一致,比如用同一个WiFi 2、真机自动调试…...

最新Next 14快速上手基础部分
最新Next 14快速上手基础部分 最新的NEXT快速上手文档,2023.10.27 英文官网同步,版本Next14.0.0 本项目案例:GitHub地址,可以根据git回滚代码到对应知识,若有错误,欢迎指正! 一、介绍 1.什么是…...

【uniapp/uview】Collapse 折叠面板更改右侧小箭头图标
最终效果是这样的: 官方没有给出相关配置项,后来发现小箭头不是 uview 的图标,而是 unicode 编码,具体代码: // 箭头图标 ::v-deep .uicon-arrow-down[data-v-6e20bb40]:before {content: \1f783; }附一个查询其他 u…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
