宋浩高等数学笔记(三)微分中值定理
首先是考研大纲包含的内容:
1.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理.
2.掌握用洛必达法则求未定式极限的方法.
3.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.
4.会用导数判断函数图形的凹凸性(注:在区间 内,设函数 具有二阶导数。当f"(x)>0 时,f(x) 的图形是凹的;当f"(x)<0时,f(x) 的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形。
5.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.
目录
3.1微分的定义and基本公式与法则
3.2微分的几何意义
3.3微分中值定理
3.4洛必达法则
3.5泰勒公式
3.6函数的单调性与曲线的凹凸性
3.7极值及其求法
3.8函数图像
3.9曲率
关于泰勒公式,洛必达法则,柯西中值定理等重要概念的总结,有助于基础的理解。
- 微分的本质就是,x或y发生极小的变化
- 如果在一一点处,y的微分可以用x的微分*一个线性主部,并加上一个高阶无穷小,则称fx在该点处可微~
- 要明确的是,可微与可导互为充要条件
- 可微的充分性是:微分之比的极限值是所谓的线性主部——换句话说,导数在邻域内部都存在
- 可微的必要性是:函数在该点必连续
- 微商的定义是两个微分的商,但是对于微商来说分子和分母是可分离的,这一点和导数不同~
- 复合函数的微分,和复合求导法的方式一致
- 微分的几何意义,本质上就是变化量的近似值,利用这一点可以计算很多函数的近似值~
3.1微分的定义and基本公式与法则
3.2微分的几何意义


- 费马引理是在说,如果在某点处取到极值,则在该邻域内导数为0
- 罗尔定理是在说,如果闭区间连续、开区间可导,且端点处函数值相等,则区间内必有一点处导数为0~
- 拉格朗日中值定理在说,闭区间连续、开区间可导,则函数图线上总有一点处的导数,与围成人的三角形斜率相同~
- 而柯西中值定理,则是更一般化的情况,是将a/b两个区间端点也该为了函数,本质上就是参数方程化
3.3微分中值定理


- 洛必达法则指的是,当一个分式的分子和父母均趋于无穷或0时,则他们比值的极限相当于上下各求一次导的极限
- 泰勒公式指的是,原函数可以展成由导数复合而成的多项式,这在计算较为复杂函数的极限时效果拔群~
3.4洛必达法则
3.5泰勒公式


- 对于函数的单调性,我们可以初步认为一阶导大于0单调增,否则单调减,所谓驻点指的是一阶导数为0的点
- 对于函数的凸凹性,我们认为二阶导数大于0是凹函数,否则为凸函数,拐点是指二阶导为0的点
- 对于极值点和凹凸性变化的点,以及拐点和驻点的判别等,要熟悉区别
- 有关单调区间、驻点拐点等的判断比较简单,这里不再赘述~
3.6函数的单调性与曲线的凹凸性
3.7极值及其求法
3.8函数图像
3.9曲率


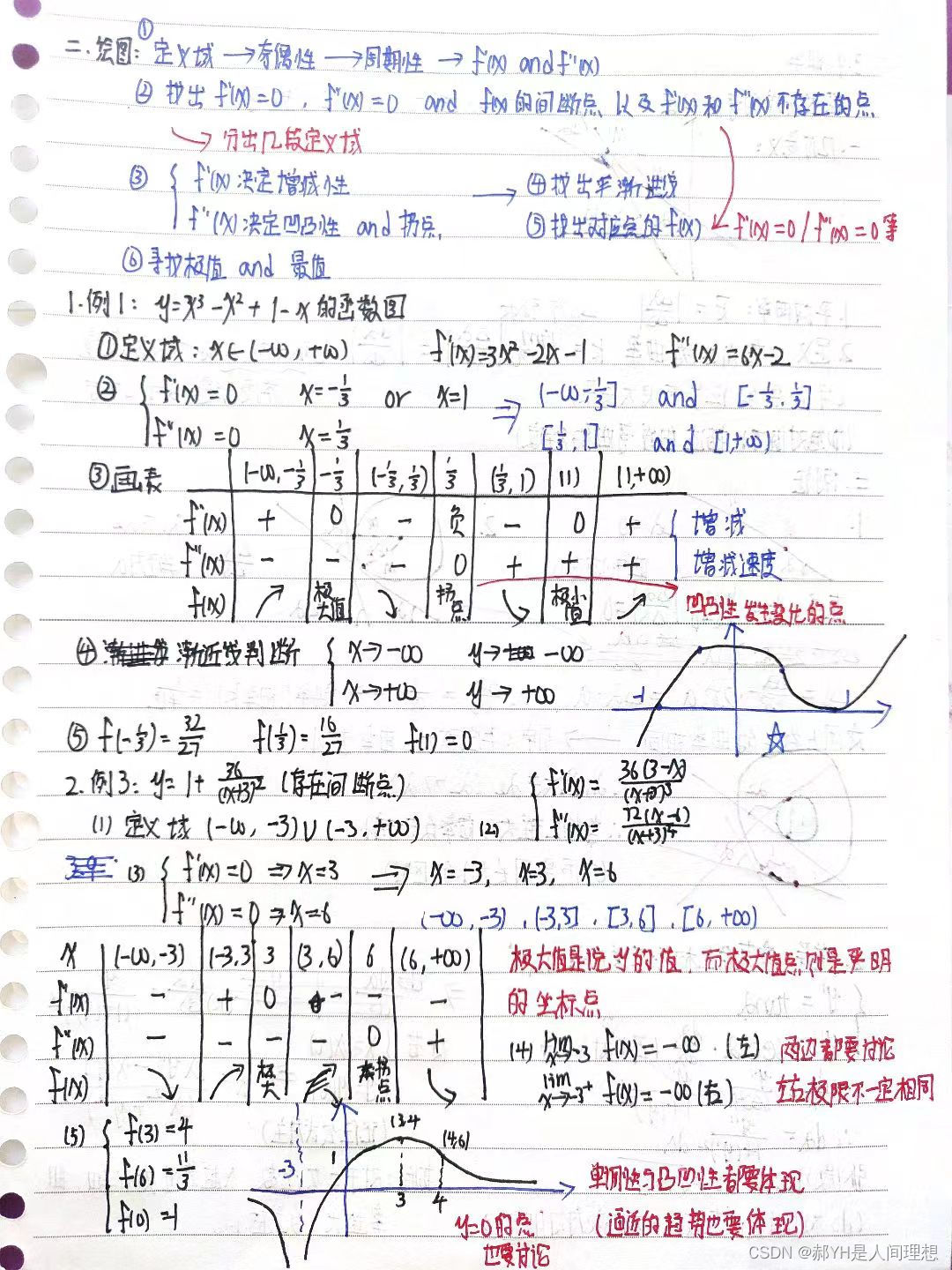
- 曲率的定义是,角度变化量和弧长变化量的极限值~

相关文章:

宋浩高等数学笔记(三)微分中值定理
首先是考研大纲包含的内容: 1.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理. 2.掌握用洛必达法则求未定式极限的方法. 3.理解函数的极值概念,掌握用导数判断函数的单调性和求函…...
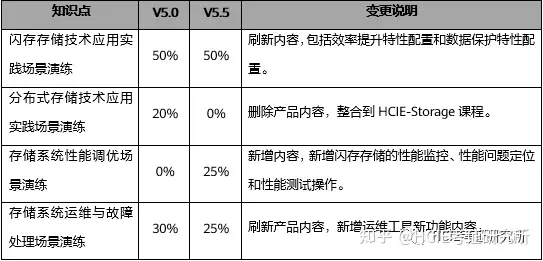
华为认证 | 11月底这门HCIP认证即将发布!
非常荣幸地通知您,华为认证HCIP-Storage V5.5(中文版)预计将于2023年11月30日正式对外发布。为了帮助您做好学习、培训和考试计划,现进行预发布通知,请您关注。 01 发布概述 基于“平台生态”战略,围绕“云…...

U-Mail邮件系统安全登录解决方案
企业邮箱是企业对内对外商务往来的主要通信工具,并且企业邮箱里面还包含了大量企业内部隐私信息、商业机密等,很容易成为黑客的攻击目标。其中邮件盗号是企业邮箱遭受攻击的主要形式,一旦企业邮箱密码被黑客盗取,黑客不仅可以利用…...

在Java继承关系中变量访问规则
首先示例代码如下: class A{public int x 0;public int get() {return x;}}class AA extends A{public int x 1; }class AAA extends AA {public int x 2;public int get() {return x;}public static void main(String[] args) {A a new AA();System.out.pri…...
)
11. 一文快速学懂常用工具——网络工具(下)
本章讲解知识点 引言curltcpdumpwireshark本专栏适合于软件开发刚入职的学生或人士,有一定的编程基础,帮助大家快速掌握工作中必会的工具和指令。本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。如专栏内容有错漏,欢迎在评论区指出或私聊我更改,一起学习,共同进…...
什么GAN生成对抗网络?生成对抗网络可以干什么?
生成对抗网络(Generative Adversarial Nets,简称GAN)。神经网络分很多种,有普通的前向传播网络,有分析图片的CNN卷积神经网络,有分析系列化数据比如语言、文字的RNN循环神经网络,这些神经网络都是用来输入数据,得到想要的结果,我们看中的是这些神经网络中很好地将数据与…...

采集Prestashop独立站
这是一个用Lua编写的爬虫程序,用于采集Prestashop独立站的内容。爬虫程序使用代理信息:proxy_host: jshk.com.cn。 -- 首先,我们需要导入所需的库 local http require(socket.http) local url require(socket.url)-- 然后,我们…...

通过一道题目带你深入了解WAF特性、PHP超级打印函数、ASCII码chr()对应表等原理[RoarCTF 2019]Easy Calc 1
题目环境: 依此输入以下内容并查看回显结果 11 1’ index.php ls 到这里没思路了 F12查看源代码 一定要仔细看啊,差点没找到,笑哭 访问calc.php文件 果然有点东西 PHP代码审计 error_reporting(0);关闭错误报告 通过GET方式传参的参数num sho…...
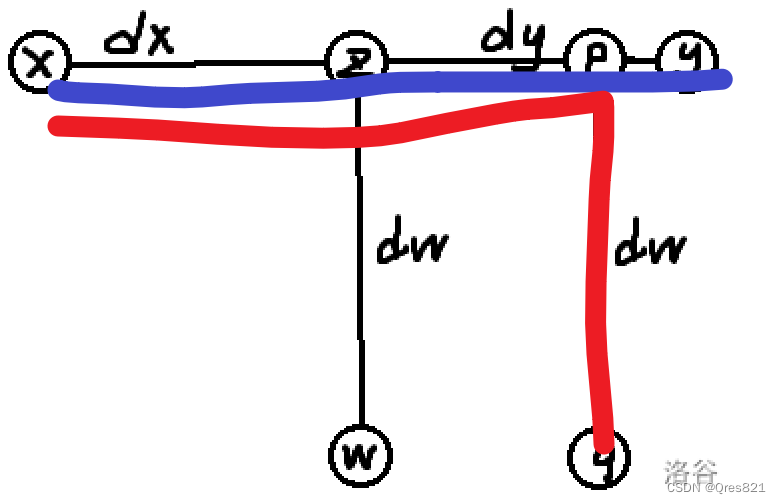
类直径树上贪心
http://cplusoj.com/d/senior/p/SS231109C 场上想到枚举点,然后最大值为高,然后可以求最大值。但是感觉计数会重 计数其实不会重,如图中,红色线段显然比蓝色线段优 所以我们枚举3叉点时没错的 #include<bits/stdc.h> usin…...
求职招聘小程序源码系统+社交招聘+多城市招聘 带完整搭建教程
大家好,今天罗峰来给大家分享一款求职招聘小程序源码系统。目前,求职招聘市场在不断变革。传统的招聘网站已经无法满足人们对于高效、便捷、多元化的招聘需求。该系统集求职招聘、社交招聘、多城市招聘等功能于一体,旨在为用户提供更加便捷、…...

Java Web 安全实战:从登录到退出
Java Web 安全实战:从登录到退出 1. 介绍 在当今互联网时代,用户信息安全至关重要。在Java Web开发中,Spring Security是一个强大且灵活的身份验证和访问控制框架,它可以帮助我们构建安全可靠的应用程序。本文将介绍如何使用Spr…...

08.Diffusion Model数学原理分析(下)
文章目录 denoising matching term σ t z \sigma_tz σtz的猜想Diffusion Model for SpeechDiffusion Model for TextMask-Predict 部分截图来自原课程视频《2023李宏毅最新生成式AI教程》,B站自行搜索。 书接上文。 denoising matching term E q ( x t ∣ x 0 …...

什么样的CRM系统更适合外贸企业?
外贸CRM系统作为外贸客户关系管理的工具,已经成为了当下外贸企业对外贸易过程中不可或缺的一环。那什么样的CRM系统更适合外贸企业?小Z向您推荐Zoho CRM。下面说说它到底有什么好处和作用。 一、搭建更高效的客户关系管理系统 外贸企业从前期推广、开发…...

selenium自动化测试入门 —— 键盘鼠标事件ActionChains
在使用 Selenium WebDriver 做自动化测试的时候,会经常模拟鼠标和键盘的一些行为。比如使用鼠标单击、双击、右击、拖拽等动作;或者键盘输入、快捷键使用、组合键使用等模拟键盘的操作。在 WebDeriver 中,有一个专门的类来负责实现这些测试场…...
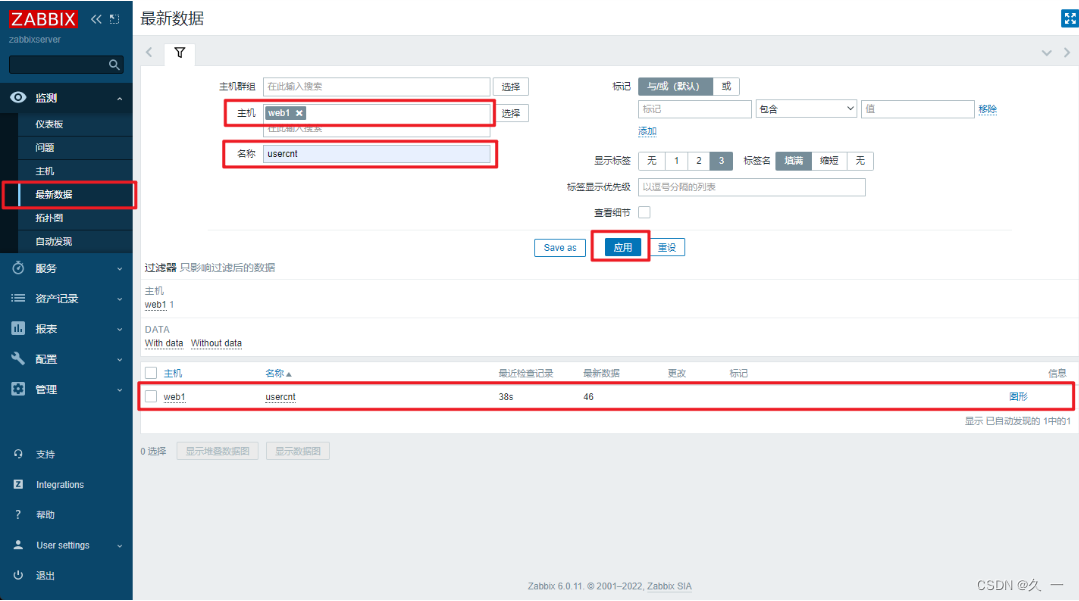
高级运维学习(十四)Zabbix监控(一)
一 监控概述 1 监控的目的 (1)报告系统运行状况 每一部分必须同时监控内容包括吞吐量、反应时间、使用率等 (2)提前发现问题 进行服务器性能调整前,知道调整什么找出系统的瓶颈在什么地方 2 监控的资源类别 …...

vite + electron引入itk报错
代码 import { readImageArrayBuffer } from itk-wasm console.log(readImageArrayBuffer)通过itk-wasm官网,创建新的项目vitevue(vue2或者vue3),都没问题。加入electeon后包此错。通过排查,意外找到原因,…...
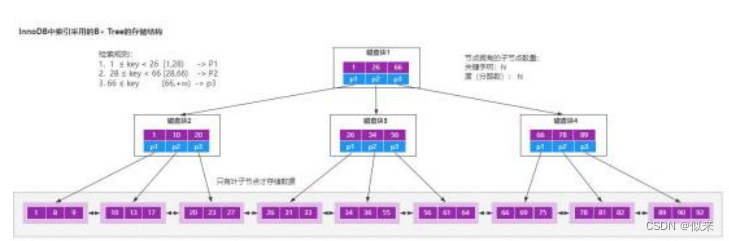
大厂面试题-MySQL为什么使用B+Tree作为索引结构
从几个方面来回答: 首先,常规的数据库存储引擎,一般都是采用B树或者B树来实现索引的存储。 (如图)因为B树是一种多路平衡树,用这种存储结构来存储大量数据,它的整个高度会相比二叉树来说,会矮很多。 而对…...

Tomcat的Engine容器
https://tomcat.apache.org/tomcat-10.1-doc/config/engine.html Engine元素代表与一个特定的Catalina Service关联的、整体的请求处理系统。它从一个或多个Connector接收并处理请求、返回完整的响应给Connector,以便最终传输给客户端。 在Service元素内部…...

vscode绿色行数设置
"workbench.colorCustomizations": {"editorLineNumber.foreground": "#00ff00"},...
闪站侠洗衣洗鞋管理系统app小程序开发;
闪站侠洗护软件系统为您提供全面的洗衣洗鞋解决方案,系统多门店,多网点。为您开通公中号小程序,并与顺丰、天猫、抖音、美团点评等第三方平台紧密连接。 我们解决洗衣工厂/门店的五大问题: 一、效率 从门店收衣到工厂出库…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
