BERT和ChatGPT简单对比
OpenAI发布了第一个版本的GPT(Generative Pretrained Transformer)模型在2018年6月。
谷歌的BERT模型(Bidirectional Encoder Representations from Transformers)是在2018年10月发布的。
BERT和ChatGPT都是由人工智能研究实验室OpenAI开发的语言处理模型,但它们在设计和用途上存在不同的特点,因此很难直接比较哪一个更好。这主要取决于你打算如何使用这些模型。
BERT(Bidirectional Encoder Representations from Transformers)是一种预训练的深度学习模型,用于自然语言处理(NLP)。它使用了Transformer的编码器,并且在预训练阶段学习了双向上下文,这使得它在理解文本语义方面表现出色。它被广泛用于各种NLP任务,如文本分类、命名实体识别(NER)等。
相比之下,ChatGPT是一个基于GPT(Generative Pretrained Transformers)的语言生成模型,它是设计用于对话应用的。GPT是一个生成模型,可以生成逼真的人类文本。ChatGPT在有监督的学习环境中被训练,以对各种提示做出有趣且相关的响应,使其在创建对话、写故事或其他生成任务方面表现得更好。
总的来说,BERT和ChatGPT各自都擅长处理特定类型的NLP任务,因此你可以根据自己的需求选择其中的一个模型。如果你需要理解和提取文本的信息,BERT可能是个好选择;如果你需要生成自然和连贯的文本,那么ChatGPT可能会更有用。
相关文章:

BERT和ChatGPT简单对比
OpenAI发布了第一个版本的GPT(Generative Pretrained Transformer)模型在2018年6月。 谷歌的BERT模型(Bidirectional Encoder Representations from Transformers)是在2018年10月发布的。 BERT和ChatGPT都是由人工智能研究实验室…...

又一重要合作,创邻科技华为云联营产品正式发布
近日,创邻科技旗下的“Galaxybase高性能图平台”正式入驻华为云云商店联营商品,创邻科技成为华为云在数据库与缓存领域的联营联运合作伙伴。通过联营联运模式,双方合作能够深入产品、生态、解决方案等多个领域,助力各行业用户数字…...

PHP+Swoole应用示例
**Swoole是一个C编写的基于异步事件驱动和协程的并行网络通信引擎,为PHP提供高性能网络编程支持** ## ⚙️ 快速启动 可以直接使用 [Docker](https://github.com/swoole/docker-swoole) 来执行Swoole的代码,例如: bash docker run --rm php…...

3线硬件SPI+DMA驱动 HX8347 TFT屏
3线硬件SPIDMA驱动 HX8347 TFT屏,实现用DMA清屏。 参考:基于stm32 标准库spi驱动st7789彩屏TFT(使用DMA)-技术天地-深圳市修德电子有限公司 一、源码 HX8347.h #ifndef USER_HX8347_H_ #define USER_HX8347_H_#define SPI_hardware #define SPI_hardw…...

实验语音学的基本概念
语音学 实验语音学只是语音学的一个分支,那么语音学到底是研究什么的呢?我们先有一个大致了解。 语音学是研究语言声音体系的学科。语音学的任务是研究说明语音的性质,内部结构和单位,语音的分类和组合,语音的产生、…...

市场上ios签名公司做什么的?
iOS签名公司是提供iOS应用程序签名服务的公司。它们为开发者提供了一种简单的方式来将他们的应用程序发布到iOS设备上,同时也为用户提供了一种下载和安装这些应用程序的方法。这些公司提供的签名服务包括苹果企业签名和开发者签名,其中企业签名是为企业开…...

12. 一文快速学懂常用工具——docker 命令
本章讲解知识点 Docker 引擎Docker 常用命令Docker 生命周期详解Containerd 与 Docker 命令对比本专栏适合于软件开发刚入职的学生或人士,有一定的编程基础,帮助大家快速掌握工作中必会的工具和指令。本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。如专栏内容有错…...
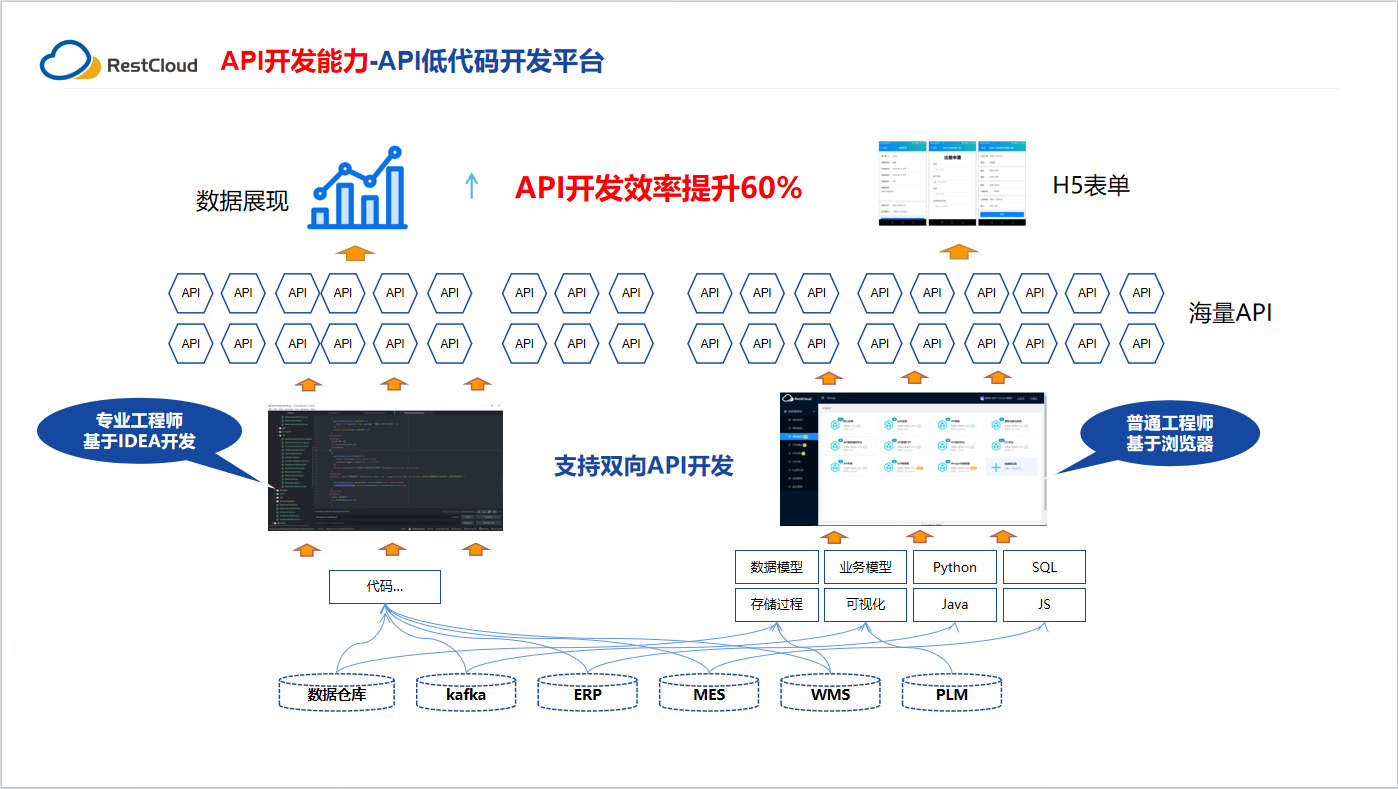
API低代码开发应用场景
什么是API低代码开发平台 API低代码开发平台是一种基于低代码开发的技术平台,它可以帮助企业快速构建和部署API应用程序。该平台通过提供可视化的开发工具、预定义的组件和模板、自动化的代码生成等功能,使得开发者可以在不需要编写大量代码的情况下&am…...

从零开始搭建React+TypeScript+webpack开发环境-性能优化
前言 当我们开发React应用时,性能始终是一个重要的考虑因素。随着应用规模的增长,React组件的数量和复杂性也会相应增加,这可能会导致性能问题的出现。在这篇博文中,我们将探讨如何通过一系列的技巧和最佳实践来优化React应用的性…...

sCrypt 现在支持 Ordinals 了
比特币社区对 1Sat Ordinals 的接受度正在迅速增加,已有超过 4800 万个铭文被铸造,这一新创新令人兴奋不已。 尽管令人兴奋,但 Ordinals 铭文的工具仍然不发达,这使得使用 Ordinals 进行构建具有挑战性。 更具体地说,缺…...

乌班图搭建 LAMP
搭建 LAMP(Linux、Apache、MySQL、PHP)堆栈是在 Ubuntu 上构建 Web 服务器的常见任务。以下是一些步骤,指导如何在 Ubuntu 上搭建 LAMP 环境: 步骤: 更新系统软件包: 在终端中执行以下命令,确…...

【Unity细节】Unity中的Transform.SetParent还有你不知道的细节
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 😶🌫️收录于专栏:unity细节和bug 😶🌫️优质专栏 ⭐【…...

php生成个性二维码
本篇引用 QRcode PHP QR Code download | SourceForge.net 无需composer即可生成 下载后的类文件是一个压缩包,里边包含很多文件和演示demo,我们只需要里的phpqrcode.php这一个文件就可以生成二维码了。它是一个多个类的集合文件,我们只用…...

css排版—— 一篇优雅的文章(中英文) vs 聊天框的特别排版
文章 <div class"contentBox"><p>这是一篇范文——仅供测试使用</p><p>With the coming of national day, I have a one week holiday. I reallyexpect to it, because it want to have a short trip during these days. Iwill travel to Ji…...

2022最新版-李宏毅机器学习深度学习课程-P46 自监督学习Self-supervised Learning(BERT)
一、概述:自监督学习模型与芝麻街 参数量 ELMO:94MBERT:340MGPT-2:1542MMegatron:8BT5:11BTuring NLG:17BGPT-3:175BSwitch Transformer:1.6T 二、Self-supervised Lear…...
【MySQL习题】各个视频的平均完播率【全网最详细教学】
目录 数据表描述 问题描述 输出示例 解题思路【重点】 正解代码 数据表描述 有以下两张表: 表1:用户-视频互动表tb_user_video_log 数据举例: 说明: uid-用户ID,video_id-视频ID start_time-开始观看时间end_time-结束观…...
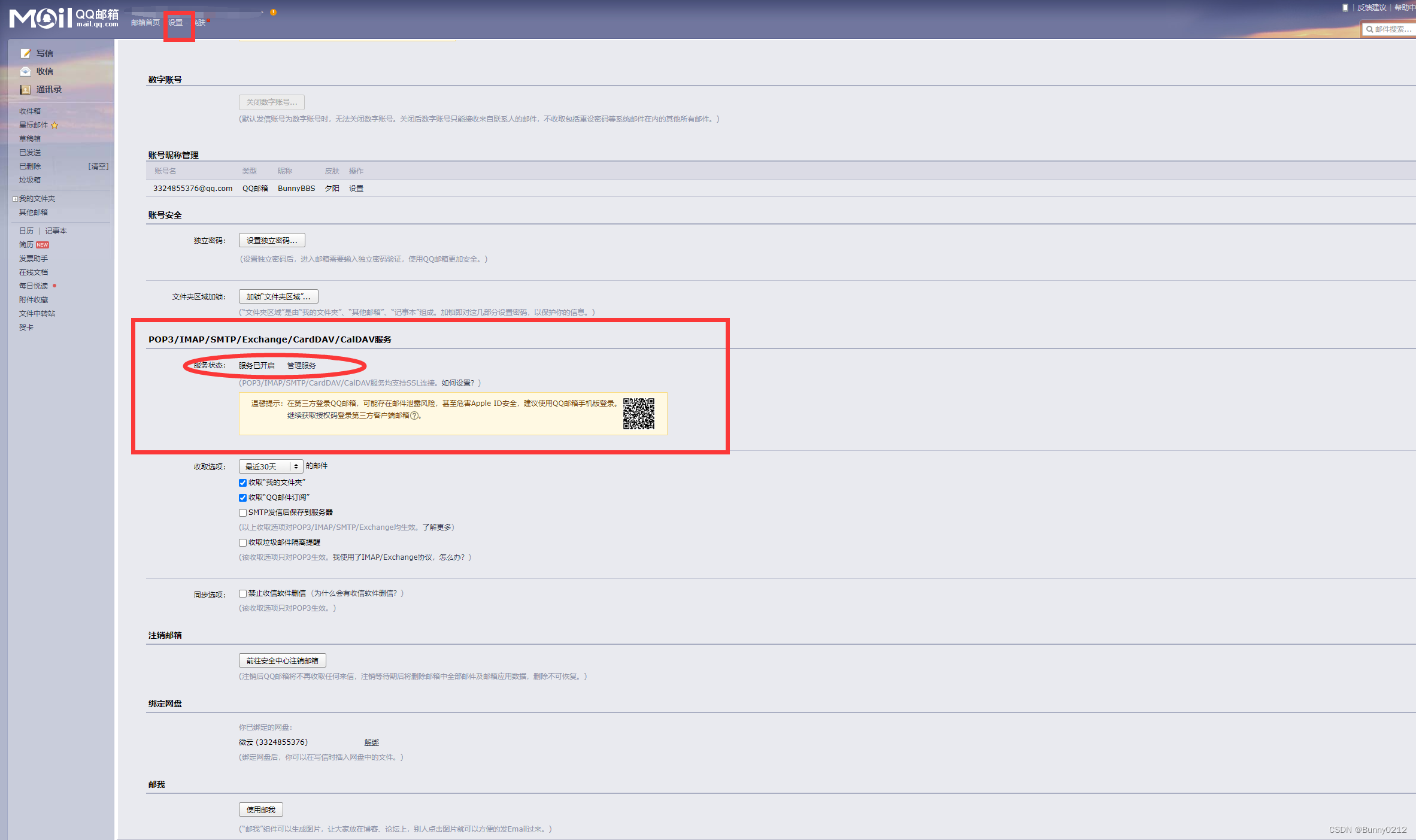
Linux Centos配置邮件发送
Linux Centos配置邮件发送 这里使用的是外部发送邮件方式,也就是使用自己的账号发送 第一步 首先要开启STMP授权码,以QQ邮箱为例 配置文件 vim /etc/mail.rc找到之后在最下面添加如下 #邮箱set from3324855376qq.com #默认smtp发送,stmp…...

宋浩高等数学笔记(三)微分中值定理
首先是考研大纲包含的内容: 1.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理. 2.掌握用洛必达法则求未定式极限的方法. 3.理解函数的极值概念,掌握用导数判断函数的单调性和求函…...
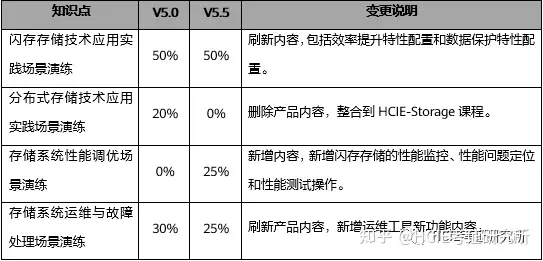
华为认证 | 11月底这门HCIP认证即将发布!
非常荣幸地通知您,华为认证HCIP-Storage V5.5(中文版)预计将于2023年11月30日正式对外发布。为了帮助您做好学习、培训和考试计划,现进行预发布通知,请您关注。 01 发布概述 基于“平台生态”战略,围绕“云…...

U-Mail邮件系统安全登录解决方案
企业邮箱是企业对内对外商务往来的主要通信工具,并且企业邮箱里面还包含了大量企业内部隐私信息、商业机密等,很容易成为黑客的攻击目标。其中邮件盗号是企业邮箱遭受攻击的主要形式,一旦企业邮箱密码被黑客盗取,黑客不仅可以利用…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
