CSDN每日一题学习训练——Java版(克隆图、最接近的三数之和、求公式的值)
版本说明
当前版本号[20231109]。
| 版本 | 修改说明 |
|---|---|
| 20231109 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 克隆图
- 题目
- 解题思路
- 代码思路
- 参考代码
- 最接近的三数之和
- 题目
- 解题思路
- 代码思路
- 参考代码
- 求公式的值
- 题目
- 解题思路
- 代码思路
- 参考代码
克隆图
题目
给你无向 连通(https://baike.baidu.com/item/连通图/6460995?fr=aladdin) 图中一个节点的引用,请你返回该图的 深拷贝(https://baike.baidu.com/item/深拷贝/22785317?fr=aladdin)(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List neighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
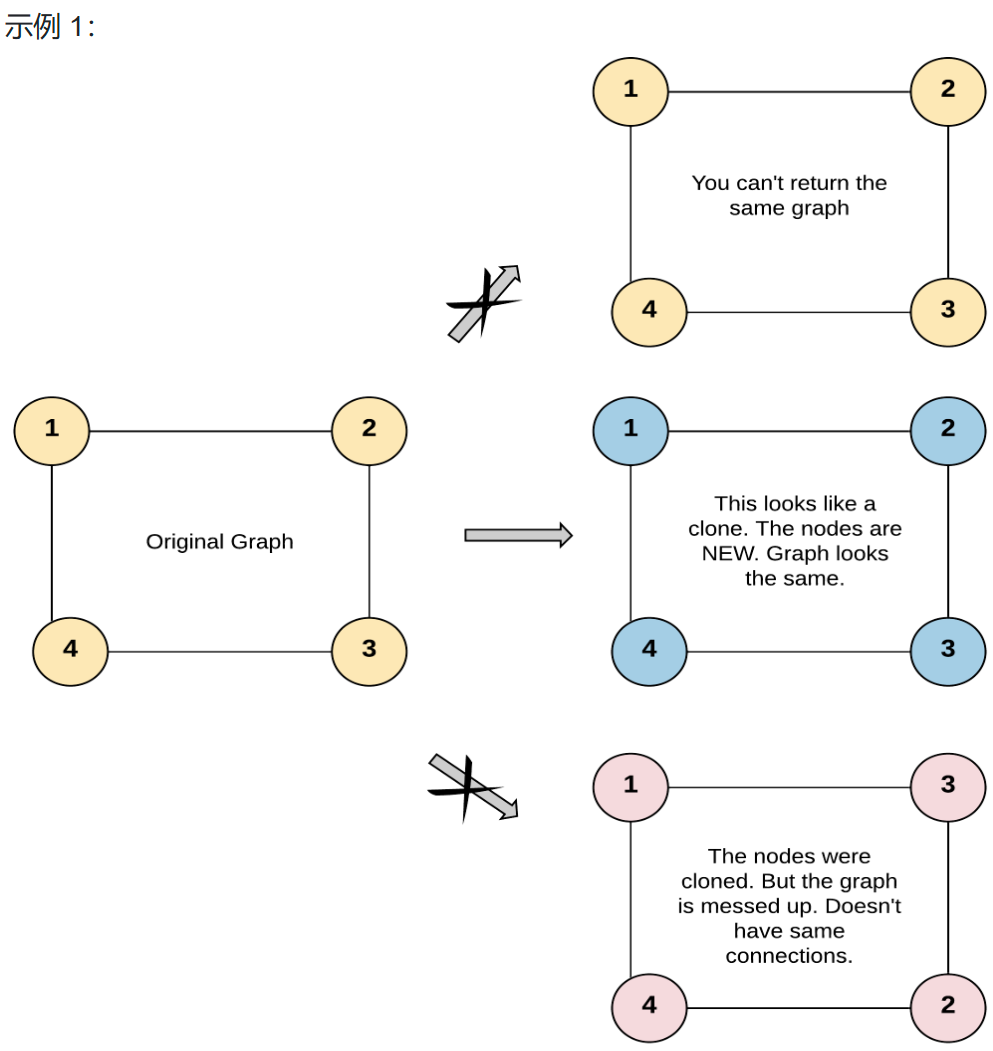
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
示例 2:

输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。
示例 4:
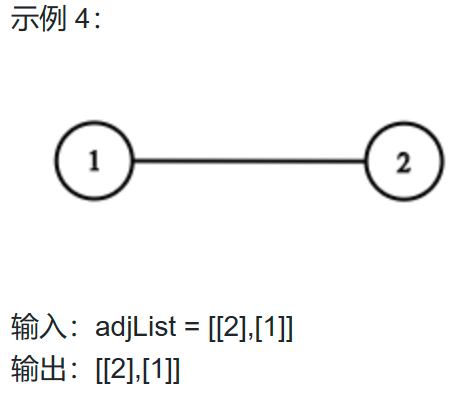
输入:adjList = [[2],[1]]
输出:[[2],[1]]
提示:
节点数不超过 100 。
每个节点值 Node.val 都是唯一的,1 <= Node.val <= 100。
无向图是一个简单图(https://baike.baidu.com/item/简单图/1680528?fr=aladdin),这意味着图中没有重复的边,也没有自环。
由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
图是连通图,你可以从给定节点访问到所有节点。
解题思路
- 创建一个哈希表,用于存储已访问过的节点及其对应的克隆节点。
- 使用深度优先搜索(DFS)遍历原图,对于每个节点: a. 如果该节点已经被访问过,则直接返回其克隆节点。 b. 创建一个新的克隆节点,并将其添加到哈希表中。 c. 遍历该节点的邻居列表,递归调用DFS函数,将邻居节点的克隆节点添加到克隆节点的邻居列表中。
- 返回克隆图的任意一个节点即可。
代码思路
-
首先定义了一个名为
Node的类,表示图中的节点,包含一个整数值val和指向左右子节点的指针left和right,以及指向下一个节点的指针next。class Node {public int val; // 节点的值public Node left; // 左子节点public Node right; // 右子节点public Node next; // 下一个节点 } -
同时,还定义了一个名为
Solution的类,其中包含了两个方法:cloneGraph和DFS。 -
cloneGraph方法是主要的入口点,它接受一个Node类型的参数node,表示要克隆的图的起始节点。// 克隆图的方法,接收一个节点作为参数public Node cloneGraph(Node node) -
该方法首先创建一个空的哈希表
visited,用于存储已经访问过的节点及其对应的克隆节点。然后调用DFS方法进行深度优先搜索,从起始节点开始遍历整个图,并返回克隆后的图的根节点。// 创建一个哈希表,用于存储已访问过的节点HashMap<Node, Node> visited = new HashMap<>();// 调用深度优先搜索方法进行克隆return DFS(node, visited); -
DFS方法是一个递归方法,用于实现深度优先搜索。它接受两个参数:当前节点node和一个哈希表visited,用于记录已经访问过的节点及其对应的克隆节点。// 深度优先搜索方法,接收一个节点和一个哈希表作为参数public Node DFS(Node node, HashMap<Node, Node> visited) -
在方法内部,首先判断当前节点是否为空,如果为空则直接返回。接着判断当前节点是否已经被访问过,如果已经访问过则直接返回其对应的克隆节点。然后创建一个新的克隆节点
clone,并将其添加到visited哈希表中。// 如果节点为空,返回空节点if (node == null) {return node;}// 如果哈希表中已经存在该节点的克隆,直接返回克隆节点if (visited.containsKey(node)) {return visited.get(node);}// 创建一个新的克隆节点,值为原节点的值,邻居列表为空Node clone = new Node(node.val, new ArrayList<>());// 将原节点和克隆节点添加到哈希表中visited.put(node, clone); -
最后,遍历当前节点的所有邻居节点,对每个邻居节点递归调用
DFS方法,并将返回的克隆节点添加到当前节点的克隆节点的邻居列表中。最终返回当前节点的克隆节点。// 遍历原节点的邻居节点,递归调用DFS方法进行克隆,并将克隆后的邻居节点添加到克隆节点的邻居列表中for (Node n : node.neighbors) {clone.neighbors.add(DFS(n, visited));}// 返回克隆节点return clone; -
这段代码实现了一个简单的图的深度优先搜索和克隆过程,可以用于处理一些需要复制或克隆图结构的场景。
参考代码
class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
class Solution {public Node cloneGraph(Node node) {HashMap<Node, Node> visited = new HashMap<>();return DFS(node, visited);}public Node DFS(Node node, HashMap<Node, Node> visited) {if (node == null) {return node;}if (visited.containsKey(node)) {return visited.get(node);}Node clone = new Node(node.val, new ArrayList<>());visited.put(node, clone);for (Node n : node.neighbors) {clone.neighbors.add(DFS(n, visited));}return clone;}
}
最接近的三数之和
题目
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
提示:
3 <= nums.length <= 10^3
-10^3 <= nums[i] <= 10^3
-10^4 <= target <= 10^4
解题思路
- 首先对数组进行排序,这样可以方便后续的查找操作。
- 使用两层循环遍历数组中的每两个数的组合,计算它们的和,记为
twoSum。 - 对于每个
twoSum,我们需要找到一个与它最接近的数,使得这三个数的和与目标值target最接近。我们可以使用递归的方法来实现这个功能。具体来说,我们可以定义一个函数oneSumCloset,它接受五个参数:数组nums、两个整数i和j表示当前考虑的两个数在数组中的位置、一个整数start和end表示在数组中查找的范围、以及目标值target。 - 在
oneSumCloset函数中,我们首先处理边界情况。如果start等于i或j,则将start加1;如果end等于i或j,则将end减1。接下来,我们判断start和end的关系。如果它们相等,说明已经找到了与target最接近的数,直接返回该数即可。如果它们相差为1,说明只有一个数与target最接近,比较这两个数与target的差值,返回差值较小的那个数。否则,我们计算中间位置middle,并根据nums[middle]与target的大小关系来更新查找范围。然后递归调用oneSumCloset函数,继续查找。 - 在主函数
threeSumClosest中,我们初始化最小值为0,并设置一个布尔变量hasMin为false,用于标记是否已经找到了与目标值最接近的三个数。然后使用两层循环遍历数组中的每两个数的组合,计算它们的和,记为twoSum。接着,我们调用oneSumCloset函数,找到与twoSum最接近的数,记为restClost。最后,我们计算这三个数的和newValue,并与当前最小值进行比较。如果找到了更接近目标值的三个数,更新最小值和hasMin。 - 当两层循环结束后,返回最小值
minValue即可。
代码思路
它包含两个方法:oneSumCloset和threeSumClosest。
-
oneSumCloset方法:这个方法用于在一个有序数组中找到与给定目标值最接近的数。它接受6个参数:一个整数数组nums,两个整数i和j,表示要搜索的范围,以及三个整数start、end和target,分别表示搜索的起始位置、结束位置和目标值。
-
方法首先检查start和end是否等于i或j,如果是,则将它们分别加1或减1。
// 在数组nums中,从i到j范围内查找与target最接近的数int oneSumCloset(int[] nums, int i, int j, int start, int end, int target) {if (start == i || start == j) // 如果start等于i或j,则将start加1start = start + 1; -
然后,根据start和end的值进行不同的处理。如果start和end相等,说明已经找到了与目标值最接近的数,直接返回该数。如果start和end相差1,说明只有一个数与目标值最接近,比较这两个数与目标值的差值,返回差值较小的那个数。否则,计算start和end的中间位置middle,并根据nums[middle]与目标值的大小关系,更新start或end的值。
if (end == i || end == j) // 如果end等于i或j,则将end减1end = end - 1;if (start == end) { // 如果start等于end,说明已经找到了与target最接近的数,直接返回该数return nums[start];} else if (end == start + 1 || end == start - 1) { // 如果end等于start+1或start-1,说明只有一个数与target最接近,比较这两个数与target的差值,返回差值较小的那个数if (Math.abs(nums[end] - target) > Math.abs(nums[start] - target)) {return nums[start];} else {return nums[end];}} else { // 如果以上条件都不满足,说明需要继续查找int middle = (int) Math.floor((start + end) / 2); // 计算中间位置if (nums[middle] > target) { // 如果中间位置的数大于target,说明目标数在左半部分,将end更新为middleend = middle;} else { // 如果中间位置的数小于等于target,说明目标数在右半部分,将start更新为middlestart = middle;} -
最后,递归调用oneSumCloset方法,继续在更新后的范围内查找与目标值最接近的数。
return oneSumCloset(nums, i, j, start, end, target); // 递归调用oneSumCloset方法,继续查找 -
threeSumClosest方法:这个方法用于在一个有序数组中找到三个数之和最接近给定目标值的组合。它接受两个参数:一个整数数组nums和一个整数target,分别表示输入的数组和目标值。
-
方法首先对数组nums进行排序。然后,使用两层循环遍历数组中的每对数,计算它们的和作为twoSum,并计算剩余的目标值rest。接着,调用oneSumCloset方法,在剩余的数组元素中查找与rest最接近的数作为restClost。
// 在数组nums中,查找三个数之和最接近target的组合public int threeSumClosest(int[] nums, int target) {Arrays.sort(nums); // 对数组进行排序int minValue = 0; // 初始化最小值为0boolean hasMin = false; // 初始化hasMin为false,表示还没有找到最小值for (int i = 0; i < nums.length - 2; i++) { // 遍历数组中的前n-2个数for (int j = i + 1; j < nums.length - 1; j++) { // 遍历数组中的第i+1个数到倒数第二个数int twoSum = nums[i] + nums[j]; // 计算两个数之和int rest = target - twoSum; // 计算剩余的目标值int restClost = oneSumCloset(nums, i, j, j + 1, nums.length - 1, rest); // 在剩余的数组元素中查找与rest最接近的数 -
将restClost与twoSum相加得到新的值newValue。接下来,判断是否已经找到了最小值minValue,如果没有找到,则将newValue赋值给minValue,并将hasMin设置为true。如果已经找到了最小值minValue,则比较newValue与minValue与目标值的差值d1和d2,如果d1大于d2,则将newValue赋值给minValue。
int newValue = restClost + twoSum; // 计算新的值if (!hasMin) { // 如果还没有找到最小值minValue = newValue; // 更新最小值hasMin = true; // 将hasMin设置为true,表示已经找到了最小值} else { // 如果已经找到了最小值int d1 = Math.abs(minValue - target); // 计算当前最小值与目标值的差值int d2 = Math.abs(newValue - target); // 计算新值与目标值的差值if (d1 > d2) { // 如果当前最小值的差值大于新值的差值minValue = newValue; // 更新最小值}} -
最后,返回minValue作为结果。
return minValue; // 返回最小值
参考代码
class Solution {int oneSumCloset(int[] nums, int i, int j, int start, int end, int target) {if (start == i || start == j)start = start + 1;if (end == i || end == j)end = end - 1;if (start == end) {return nums[start];} else if (end == start + 1 || end == start - 1) {if (Math.abs(nums[end] - target) > Math.abs(nums[start] - target)) {return nums[start];} else {return nums[end];}} else {int middle = (int) Math.floor((start + end) / 2);if (nums[middle] > target) {end = middle;} else {start = middle;}return oneSumCloset(nums, i, j, start, end, target);}}public int threeSumClosest(int[] nums, int target) {Arrays.sort(nums);int minValue = 0;boolean hasMin = false;for (int i = 0; i < nums.length - 2; i++) {for (int j = i + 1; j < nums.length - 1; j++) {int twoSum = nums[i] + nums[j];int rest = target - twoSum;int restClost = oneSumCloset(nums, i, j, j + 1, nums.length - 1, rest);int newValue = restClost + twoSum;;if (!hasMin) {minValue = newValue;hasMin = true;} else {int d1 = Math.abs(minValue - target);int d2 = Math.abs(newValue - target);if (d1 > d2) {minValue = newValue;}}}}return minValue;}
}
求公式的值
题目
求 1-1/2!-1/3! -… -1/10!
解题思路
- 首先,我们需要计算阶乘。在给定的代码中,已经有一个名为
jiecheng的方法用于计算阶乘。我们可以使用这个方法来计算1-1/2!-1/3! -… -1/10!的值。 - 在
sum方法中,我们需要遍历从1到n的所有整数。对于每个整数i,我们需要计算1/i!并将其累加到总和中。同时,我们需要更新变量s的值,使其在每次迭代时取反。 - 最后,在
main方法中,我们调用sum方法并传入参数n=10,然后输出结果。
代码思路
这段代码是一个Java程序,用于计算一个数列的和。该数列由以下公式生成:
sum = 1/n! + (-1)^n / (n-1)! + ... + 1/1!
-
程序中定义了两个方法:
jiecheng和sum。 -
jiecheng方法用于计算阶乘(factorial),即从1到给定整数n的所有正整数的乘积。它使用了一个循环来逐个乘以从1到n的整数,并将结果存储在变量s中。最后,该方法返回计算得到的阶乘值。// 定义一个静态方法jiecheng,接收一个整数n作为参数,返回n的阶乘public static double jiecheng(int n) {double s = 1; // 初始化变量s为1// 使用for循环计算n的阶乘for (int i = 1; i <= n; i++) {s *= i; // 将s乘以i}return s; // 返回计算结果 -
sum方法用于计算数列的和。它使用了一个循环来迭代从1到n的每个整数。在每次迭代中,它将当前项的值累加到变量sum中。每一项的值由公式1/n! + (-1)^n / (n-1)!计算得出。其中,(-1)^n表示交替的符号,(n-1)!表示n-1的阶乘。最后,该方法返回计算得到的数列和。// 定义一个静态方法sum,接收一个整数n作为参数,返回数列的和public static double sum(int n) {double sum = 0.0; // 初始化变量sum为0.0int s = 1; // 初始化变量s为1// 使用for循环计算数列的和for (int i = 1; i <= n; i++) {sum += s / jiecheng(i); // 将s除以i的阶乘加到sum上s = -s; // 将s取反}return sum; // 返回计算结果} -
在
main方法中,程序将整数n设置为10,并调用sum方法来计算数列的和。然后,它将结果打印到控制台上。
// 定义一个主方法main,程序的入口点public static void main(String[] args) throws Exception {int n = 10; // 定义变量n为10double ss = sum(n); // 调用sum方法计算数列的和,并将结果赋值给变量ssSystem.out.println(ss); // 输出数列的和}
参考代码
public class TEST {public static double jiecheng(int n) {double s = 1;for (int i = 1; i <= n; i++)s *= i;return s;}public static double sum(int n) {double sum = 0.0;int s = 1;for (int i = 1; i <= n; i++) {sum += s / jiecheng(i);s = -s;}return sum;}public static void main(String[] args) throws Exception {int n = 10;double ss = sum(n);System.out.println(ss);}
}
相关文章:

CSDN每日一题学习训练——Java版(克隆图、最接近的三数之和、求公式的值)
版本说明 当前版本号[20231109]。 版本修改说明20231109初版 目录 文章目录 版本说明目录克隆图题目解题思路代码思路参考代码 最接近的三数之和题目解题思路代码思路参考代码 求公式的值题目解题思路代码思路参考代码 克隆图 题目 给你无向 连通(https://baike.baidu.com…...

XOR Construction
思路: 通过题目可以得出结论 b1^b2a1 b2^b3a2 ....... bn-1^bnan-1 所以就可以得出 (b1^b2)^(b2^b3)a1^a2 b1^b3a1^a2 有因为当确定一个数的时候就可以通过异或得到其他所有的数,且题目所求的是一个n-1的全排列 那么求出a的前缀异或和arr之后…...
K8S容器持续Terminating无法正常关闭(sider-car容器异常,微服务容器正常)
问题 K8S上出现大量持续terminating的Pod,无法通过常规命令删除。需要编写脚本批量强制删除持续temminating的Pod:contribution-xxxxxxx。 解决 获取terminating状态的pod名称的命令: # 获取media命名空间下,名称带contributi…...

Spring 循环依赖
文章目录 内容总结循环依赖 内容总结 循环依赖 循环依赖只存在于 Spring 中, 是因为 Spring 创建 Bean 的流程中, 依赖注入阶段, 会先从单例池中找, 没有再从定义池中找, 针对定义池中找到的候选项会通过 getBean 创建其单例并缓存到单例池, 此机制导致了存在循环依赖的问题.…...

MySQL 8.0.13升级到8.0.35记录 .NET
1、修改表结构的字符集 utf8 修改成 utf8mb4 utf8_general_ci 修改成 utf8mb4_0900_ai_ci 注:所有地方都要替换。 否则会报错误提示:Character set utf8mb3 is not supported 下面是.NET环境升级遇到的问题 2、MySQL Connector Net 8.0.13 在程…...

flink udtaf 常年不能用
[FLINK-32807] when i use emitUpdateWithRetract of udtagg,bug error - ASF JIRA flink1.18发布的时候 他都显示未解决 但是文档上一直有udtaf...

路由汇总的四要点
1.是基于链路级的还是进程级的? RIP和eigrp都是基于接口的链路级汇总,而OSPF是基于进程的 2.汇总路由什么时候消失? 最后一条明细路由消失的时候,汇总路由消失。 3.汇总之后,汇总路由被通告,本地是否会产生一条指向NULL接口的…...
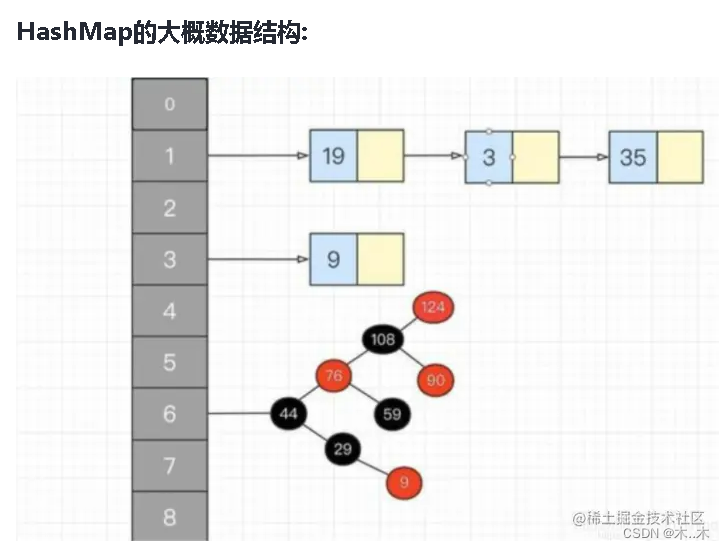
HashMap存值、取值及哈希碰撞原理分析
HashMap中的put()和get()的实现原理: map.put(k,v)实现原理 首先将k,v封装到Node对象当中(节点)。 然后它的底层会调用K的hashCode()方法得出hash值。 通过哈希表函数/哈希算法,将hash值转换成数组的下标,下标位置上…...

【SVN】
SVN 1 svn使用1.1 主干合并到分支1.2 分支合并到主干1.3 分支建立1.4 创建分支1.5 切换分支1.6 合并分支1.7 删除分支 2 概念理解 1 svn使用 1.1 主干合并到分支 首先,在本地trunk中先update一下,有冲突的解决冲突,保证trunk和repository已…...

编程语言,脚本语言
脚本语言上手快,快速实现一个小应用如python;编程语言重型,需复杂的设计和较长时间的开发,如java、c...
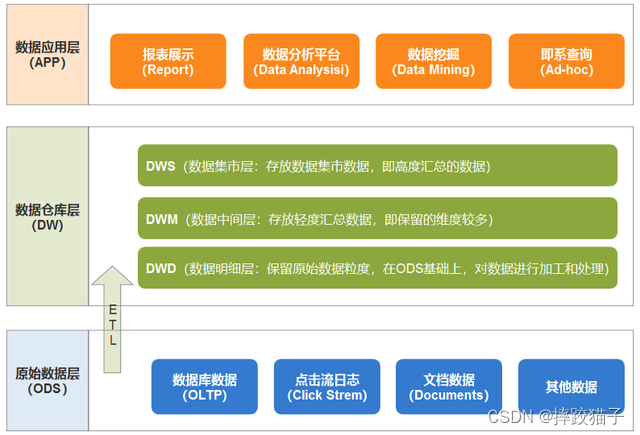
探索双十一:从技术角度剖析电商狂欢节
每年的11月11日,全球最大的在线购物狂欢节“双十一”在中国掀起了一场规模空前的消费风暴。以阿里巴巴为代表的电商平台和众多品牌商家,不仅为消费者提供了数以亿计的优惠商品,同时也将这一活动打造成了一个科技与商业完美结合的标志事件。本…...
Ubuntu LTS 坚持 10 年更新不动摇
Linux 内核开发者 Jonathan Corbet 此前在欧洲开源峰会上宣布,LTS 内核的支持时间将从六年缩短至两年,原因在于缺乏使用和缺乏支持。稳定版内核维护者 Greg Kroah-Hartman 也表示 “没人用 LTS 内核”。 近日,Ubuntu 开发商 Canonical 发表博…...

Python将多个相同格式的变量存储到列表中
在日常写代码过程中往往会遇到多个相同格式名称的变量需要存储到一个list。 怎么优雅地写出来呢 首先定义变量,然后使用列表推导式存储到列表中 # 定义变量 a_1, a_2 , # 列表推导式完成 a_list [globals()[fa_{i}] for i in range(1, 3)]...

前端字符串转数组对象实现方式-开发bug总结6
问题描述: 后台管理系统,这次投产完线上出现了个问题!element-ui组件下拉选项框打开全部都是无数据,而且控制台报错,但是新添加的数据是正常显示的。对比了原因之后发现,新的数据前端传给后端的格式&#…...
99 颜色分类
颜色分类 题解1 双指针题解2 单指针 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在…...

计算机视觉与深度学习 | 基于GPS/BDS多星座加权图因子优化的行人智能手机导航
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 基于GPS/BDS多星座加权图因子优化的行人智能手机导航 1、引言2、相关工…...
低代码平台,业务开发的“银弹”
目录 一、为什么需要低代码平台 二、低代码平台的搭建能力 三、低代码其他能力 四、写在最后 随着互联网和信息技术的快速发展,各行各业都在积极拥抱数字化转型。在这个过程中,软件开发成为企业实现数字化转型的关键环节。然而,传统的软件开发…...
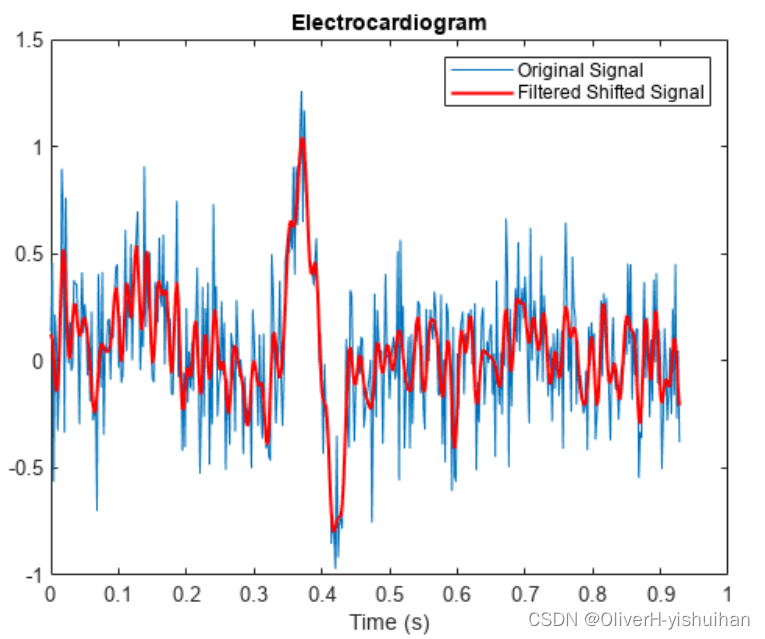
补偿 FIR 滤波器引入的延迟
补偿 FIR 滤波器引入的延迟 对信号进行滤波会引入延迟。这意味着相对于输入,输出信号在时间上有所偏移。此示例向您说明如何抵消这种影响。 有限冲激响应滤波器经常将所有频率分量延迟相同的时间量。这样,我们就很容易通过对信号进行时移处理来针对延迟…...
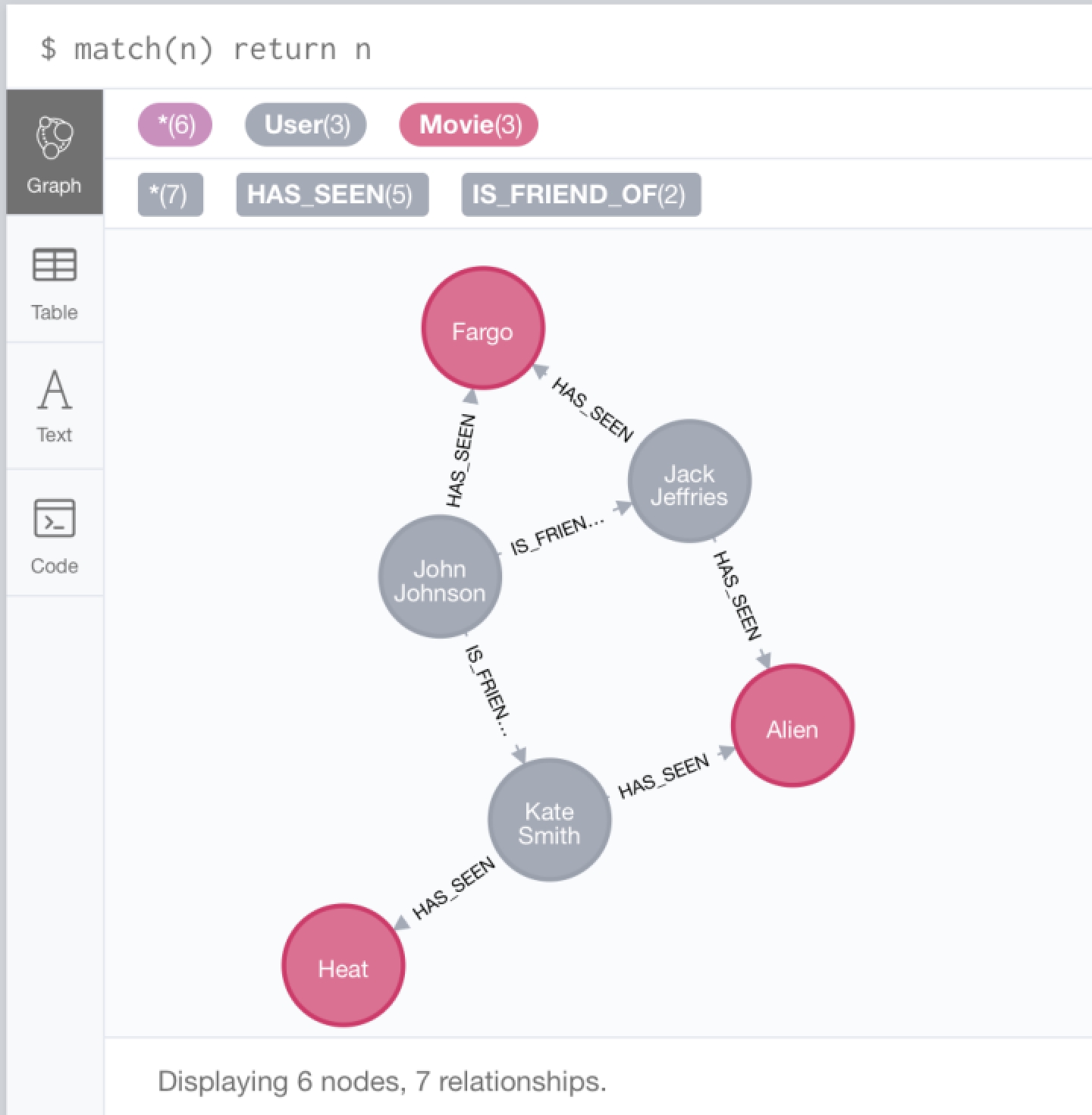
图数据库Neo4j详解
文章目录 第一章 图和Neo4j1.1 图数据库概念1.1.1 图论起源1.1.2 节点-关系及图1.1.3 图数据库1.1.4 图数据库分类1.1.4 图数据库应用场景1.1.5 与关系型数据库对比1.1.6 图数据库优势 1.2 Neo4j介绍1.2.1 Neo4j是什么1.2.2 Neo4j特点1.2.3 Neo4j的优势1.2.4 Neo4j的限制1.2.5 …...

系列一、Shiro概述
一、概述 Shiro是一款主流的Java安全框架,不依赖任何容器,可以运行在JavaSE 和 JavaEE项目中,它的主要作用是对访问系统的用户进行身份认证、授权、会话管理、加密等操作。 一句话:Shiro是一个用来解决安全管理的系统框架&#x…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
