让深度神经网络绘画以了解它们是如何工作的
一、说明
深度学习如此有效,这真是一个谜。尽管有一些关于深度神经网络为何如此有效的线索,但事实是没有人完全确定,并且深度学习的理论理解是一个非常活跃的研究领域。
在本教程中,我们将以一种不寻常的方式触及问题的一个小方面。我们将让神经网络为我们绘制抽象图像,然后我们将解释这些图像,以便对幕后可能发生的事情有更好的直觉。此外,作为奖励,在本教程结束时,您将能够生成如下所示的图像(所有内容都少于 100 行 PyTorch 代码。请在此处查看随附的 Jupyter 笔记本):

我的神经网络长大后想成为一名画家。
二、这个图像是如何生成的?
该图像是由一个称为组合模式生成网络(CPPN)的简单架构生成的,我是通过这篇博客文章介绍的。在那篇博客文章中,作者通过用 JavaScript 编写的神经网络生成抽象图像。该文的代码在 PyTorch 中实现了它们。
通过神经网络生成图像的一种方法是让它们一次性输出完整图像,如下所示,称为“生成器”的神经网络将随机噪声作为输入,并在输出层中生成整个图像(其中尺寸(宽*高)。
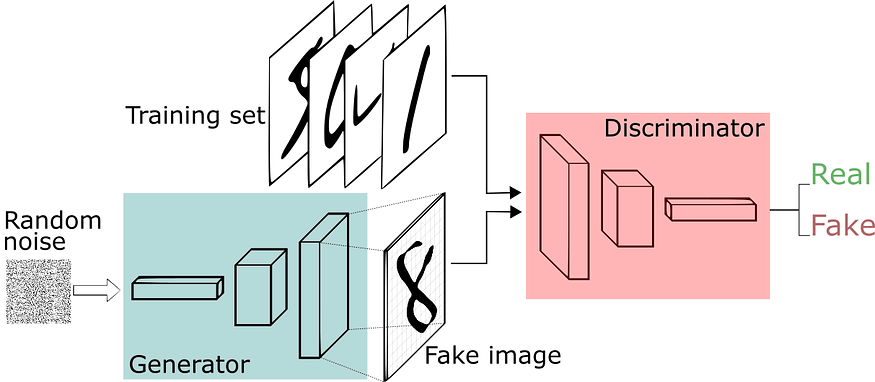
图片来自生成对抗网络简短介绍
与输出整个图像相反,CPPN(我们将要探索的架构)输出给定位置的像素颜色(作为输入输入)。

通过使用 TensorFlow 生成抽象模式的图像
忽略上图中的 z 和 r,请注意网络正在接收像素的x、y坐标并输出该像素应该是什么颜色(由c表示)。这种网络的 PyTorch 模型如下所示:
请注意,它需要 2 个输入,并有 3 个输出(像素的 RGB 值)。生成整个图像的方法是输入所需图像(特定尺寸)的所有 x,y 位置,并继续将这些 x,y 位置的颜色设置为网络输出的颜色。
三、神经网络实验
我第一次尝试运行上面看到的神经网络时,我最终生成了这些图像。

如果我有买家购买这件艺术品,我会立即卖掉它。
我花了很多时间摸不着头脑,想知道为什么无论我提供什么 x,y 位置作为输入,网络输出都是灰色的。理想情况下,这种情况不应该发生,因为对于如此深的网络。改变输入值应该改变输出值。我还知道,每次初始化神经网络时,由于其参数(权重和偏差)的随机初始化,它有可能生成全新的图像。但显然,即使经过几次尝试,我从神经网络中得到的只是这种灰色的酱缸。为什么?
我的怀疑集中在所使用的特定激活函数上:tanh。也许后续层中的多个tanh序列将所有输入数字压缩到接近 0.5。在输出层(代表灰色)。然而,我关注的博客文章也使用了tanh。我所做的就是将博客的用 JavaScript 编写的神经网络转换为 PyTorch,*没有*任何更改。
我终于找到了罪魁祸首。这就是 PyTorch 在初始化新神经网络时初始化权重的方式。根据他们的用户论坛,他们使用从 -1/sqrt(N) 到 +1/sqrt(N) 范围内随机抽取的数字来初始化权重,其中 N 是层中传入连接的数量。因此,如果隐藏层 N=16,权重将从 -1/4 初始化到 +1/4。我对为什么这会导致灰色酱缸的假设是因为权重来自一个小范围并且变化不大。
如果网络中的所有权重都在 -1/4 到 +1/4 之间,当乘以任何输入并相加时,也许会发生像中心极限定理这样的效果。
中心极限定理 (CLT) 规定,在某些情况下添加独立的随机变量,即使原始变量本身不是正态分布,它们的正确归一化总和也趋向于正态分布(非正式的“钟形曲线”)
回想一下后续层上的值是如何计算的。
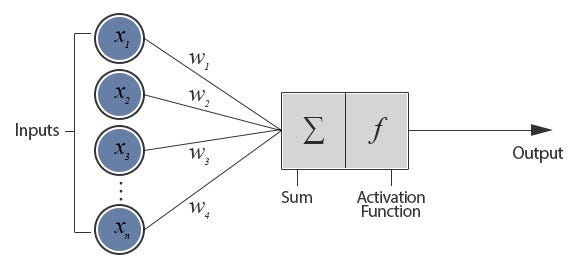
图片来自For Dummies — 我们都需要的神经网络简介!
在我们的例子中,第一个输入层有 2 个值 (x,y),第二个隐藏层有 16 个神经元。因此,第二层上的每个神经元都会获得 2 个值乘以从 -1/4 到 +1/4 得出的权重。将它们相加,然后在从激活函数tanh出发后,成为要传递到第三层的新值。
现在,从第二层开始,有 16 个输入要传递到第三层中的 16 个神经元中的每一个。想象一下,每个值都由z 表示。那么第三层每个神经元的值是:
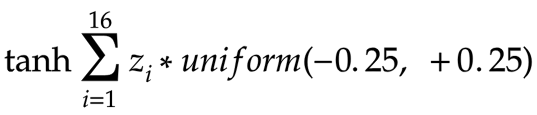
这是我们做出另一个猜测的地方。因为权重的方差较小(-1/4 到 +1/4),所以 z 的值(输入 x,y 乘以权重,然后通过tanh函数传递)也不会变化很大(因此将会类似)。所以方程可以看作:
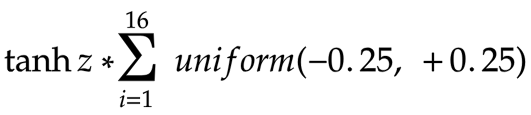
每个神经元从 -0.25 到 +0.25 的 16 个权重之和最有可能为零。即使在第一层中,总和不接近于零,网络的八层也为上述方程提供了足够的机会最终产生接近于零的值。因此,无论输入值 (x, y) 如何,进入激活函数的总值(权重总和 * 输入)始终接近零值,tanh 映射为零(因此,所有后续层中的值保持为零) )。
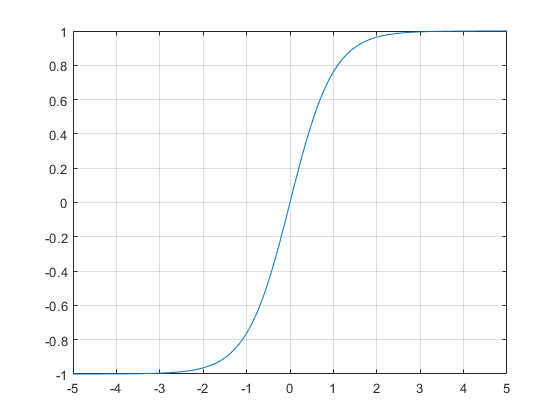
X 轴是 TanH 的输入,Y 轴是输出。请注意,0 被映射到 0。
颜色呈灰色是什么原因?这是因为 sigmoid(最后一层的激活函数)将传入值设为 0,并将其映射到 0.5(代表灰色,0 表示黑色,1 表示白色)。
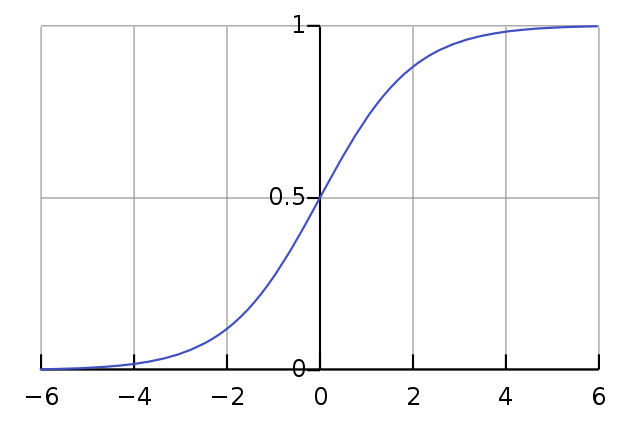
注意 Sigmoid 如何将 0 输入值映射到 0.5
四、如何修复灰色酱缸?
由于罪魁祸首是权重的微小差异,我的下一步就是增加它。我更改了默认初始化函数,将权重从 -100 分配到 +100(而不是 -1/4 到 +1/4)。现在运行神经网络,这就是我得到的:

瞧!灰色粘液现在变成了一些颜色斑点。
现在,这是一些进展。我的假设是正确的。但生成的图像仍然没有太多结构。这很简单。
这个神经网络在底层所做的就是将输入与权重相乘,将它们推入tanh,最后通过 sigmoid 输出颜色。既然我固定了权重,我可以固定输入以使输出图像更有趣吗?唔。
请注意,上面的图像是当我输入 X,Y 作为原始像素坐标时生成的,从 0,0 开始,到 128, 128(这是图像的大小)结束。这意味着我的网络从未将负数视为输入,而且由于这些数字很大(比如 X,Y 可能是 100、100),tanh要么得到一个非常大的数字(它被压缩为 +1),要么得到一个非常小的数字(它被压缩到-1)。这就是为什么我看到原色的简单组合(例如,0,1,1 的 R、G、B 输出代表您在上图中看到的青色)。
五、如何让图像变得更有趣?
就像在原来的博客文章(我正在关注的)中一样,我决定标准化 X 和 Y。因此,我不会输入 X,而是输入 (X/image_size)-0.5。这意味着 X 和 Y 的值范围为 -0.5 到 +0.5(与图像大小无关)。这样做我得到了以下图像:
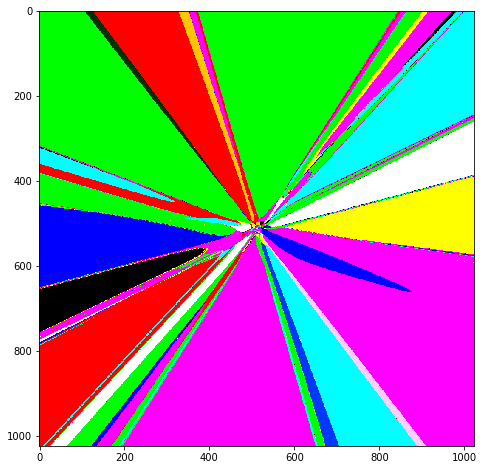
还有一些进步!
有趣的是,在上一张图像中,线条向右下角增长(因为 X、Y 值在增加)。此处,由于 X、Y 值已归一化并且现在包含负数,因此线条均匀地向外生长。然而,图像仍然不够漂亮。
六、如何让图像变得更有趣?
如果你仔细观察,你会发现在图像的中间,似乎比边缘有更多的结构。这是数学之神的暗示,我们应该放大那里去发现美。
向图像中心放大的方法有以下三种:
- 生成大图像。由于像素坐标已标准化,我们可以简单地运行神经网络来生成更大的图像。之后,我们可以通过图像编辑工具放大中间,看看我们发现了什么。
- 将 X 和 Y 输入乘以少量(缩放系数),这将有效地实现与先前方法相同的效果(并避免我们在其余不感兴趣的区域上进行浪费计算)
- 由于输出是由输入 * 权重决定的,因此我们也可以通过将权重值从 -100、+100 减少到 +3、-3 等其他值来进行缩放(同时记住不要减少太多。记住)如果权重在 -0.25 到 +0.25 范围内,就会出现灰色粘液?)
当我采用第二种方法并将 X 和 Y 乘以 0.01 时,得到的结果如下:

我称之为神经蒙德里安!
当我采用第三种方法并将权重初始化为 -3 和 +3 之间时,这是我得到的图像。

你的心已经被震撼了吗?
七、更多实验
我将权重初始化更改为正态分布(平均值为 0,标准差为 1)并生成多个图像(通过随机初始化)。



当我删除所有隐藏层(仅输入到输出映射)时:

0 个隐藏层
当我只保留一个隐藏层(而不是默认的 8 个隐藏层)时:

1个隐藏层
当我将隐藏层数量加倍至 16 时:

16 个隐藏层,每个隐藏层 16 个神经元
正如您可以想象的那样,随着隐藏层数量的增加,图像变得更加复杂。我想知道如果我不将层数加倍,而是将层数保持不变 (8),但将每层的神经元数量加倍(从 16 个增加到 32 个),会发生什么。这是我得到的:

8 个隐藏层,每个隐藏层 32 个神经元
请注意,即使在上述两种情况下网络中的权重总数相似,但具有双倍层的网络比每层具有双倍神经元的网络更加像素化。像素表明在这些区域中函数变化剧烈,因此如果我们进一步放大,就会发现更多结构。而对于具有原始层数但每层神经元数量加倍的网络,功能非常平滑,因此不太“可缩放”。
当然,所有这些都是深度使神经网络更具表现力的另一种说法。正如《论深度神经网络的表达能力》论文所建议的那样:
计算函数的复杂度随着深度呈指数增长
这正是我们所看到的。万能逼近定理表明,理论上,一个足够大的神经网络即使只有一个隐藏层也可以表达任何函数。但实际上,网络越深,输入 -> 输出映射就越复杂。
八、毫无意义但很有趣的实验
如果我们将每层的神经元数量从 8 个增加到 128 个(增加一个数量级)会怎样?

神经波洛克!
如果我们从每个隐藏层 128 个神经元开始,但在每个后续层中逐渐将它们减半,如下所示。这是我得到的:

这个看起来比其他的更“自然”。
人们可以进行“大量”更多实验并获得有趣的图像,因此我将其留在这里供您使用代码(Jupyter Notebook)。尝试更多架构、激活和层。如果您发现有趣的事情,请在 Twitter 上标记我或在 Medium 上发表评论,我将在我的网络中分享。
或者你可以将神经网络生成的图像与神经网络生成的哲学结合起来,并做出如下的东西:

九 参考代码
9.1 torch代码
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from IPython import display
from matplotlib import colors
import os, copy
from PIL import Imagedef init_normal(m):if type(m) == nn.Linear:nn.init.normal_(m.weight)class NN(nn.Module):def __init__(self, activation=nn.Tanh, num_neurons=16, num_layers=9):"""num_layers must be at least two"""super(NN, self).__init__()layers = [nn.Linear(2, num_neurons, bias=True), activation()]for _ in range(num_layers - 1):layers += [nn.Linear(num_neurons, num_neurons, bias=False), activation()]layers += [nn.Linear(num_neurons, 3, bias=False), nn.Sigmoid()]self.layers = nn.Sequential(*layers)def forward(self, x):return self.layers(x)def gen_new_image(size_x, size_y, save=True, **kwargs):net = NN(**kwargs)net.apply(init_normal)colors = run_net(net, size_x, size_y)plot_colors(colors)if save is True:save_colors(colors)return net, colorsdef run_net(net, size_x=128, size_y=128):x = np.arange(0, size_x, 1)y = np.arange(0, size_y, 1)colors = np.zeros((size_x, size_y, 2))for i in x:for j in y:colors[i][j] = np.array([float(i) / size_y - 0.5, float(j) / size_x - 0.5])colors = colors.reshape(size_x * size_y, 2)img = net(torch.tensor(colors).type(torch.FloatTensor)).detach().numpy()return img.reshape(size_x, size_y, 3)def plot_colors(colors, fig_size=4):plt.figure(figsize=(fig_size, fig_size))plt.imshow(colors, interpolation='nearest', vmin=0, vmax=1)def save_colors(colors):plt.imsave(str(np.random.randint(100000)) + ".png", colors)def run_plot_save(net, size_x, size_y, fig_size=8):colors = run_net(net, size_x, size_y)plot_colors(colors, fig_size)save_colors(colors)n,c = gen_new_image(128, 128, save=False, num_neurons=32)
plt.imshow(c)
plt.axis('on') # 关掉坐标轴为 off
plt.title('image') # 图像题目
plt.show()run_plot_save(n, 1080, 720)
for num_layers in range(2, 30, 3):print(f"{num_layers} layers")n,c = gen_new_image(128, 128, save=False, num_layers=num_layers)plt.imshow(c)plt.axis('on') # 关掉坐标轴为 offplt.title('image') # 图像题目plt.show()for i in range(1, 10, 2):print(f"{num_layers} layers")n,c = gen_new_image(128, 128, save=False, num_neurons=2**i)plt.imshow(c)plt.axis('on') # 关掉坐标轴为 offplt.title('image') # 图像题目plt.show()9.2 js代码
// actual size of generated imagevar sizeh = 320;
var sizew = 320;// settings of nnet:var networkSize = 16; // 16 neurons in each layervar nHidden = 8; // depth of 8 layersvar nOut = 3; // r, g, b layers// support variables:var img; // this is where we hold the imagevar G = new R.Graph(false); // graph object from recurrent.jsvar initModel = function() {var model = [];// define the model below:model.w_in = R.RandMat(networkSize, 3); // x, y, and biasfor (var i = 0; i < nHidden; i++) {model['w_'+i] = R.RandMat(networkSize, networkSize);}model.w_out = R.RandMat(nOut, networkSize); // output layerreturn model;
};var model = initModel();var forwardNetwork = function(G, model, x_, y_) {var x = new R.Mat(3, 1); // inputvar i;x.set(0, 0, x_);x.set(1, 0, y_);x.set(2, 0, 1.0); // bias.var out;out = G.tanh(G.mul(model.w_in, x));for (i = 0; i < nHidden; i++) {out = G.tanh(G.mul(model['w_'+i], out));}out = G.sigmoid(G.mul(model.w_out, out));return out;
};function getColorAt(x, y) {// function that returns a color given coord (x, y)var r, g, b;var out = forwardNetwork(G, model, x, y);r = out.w[0]*255.0;g = out.w[1]*255.0;b = out.w[2]*255.0;return color(r, g, b);
}// ... rest of the code populates img using getColorAt(x, y)相关文章:

让深度神经网络绘画以了解它们是如何工作的
一、说明 深度学习如此有效,这真是一个谜。尽管有一些关于深度神经网络为何如此有效的线索,但事实是没有人完全确定,并且深度学习的理论理解是一个非常活跃的研究领域。 在本教程中,我们将以一种不寻常的方式触及问题的一个小方面…...

https://www.jianshu.com/p/34bf240b85a9
https://www.jianshu.com/p/34bf240b85a9 https://www.eccee.com/soft-platform/991.html...
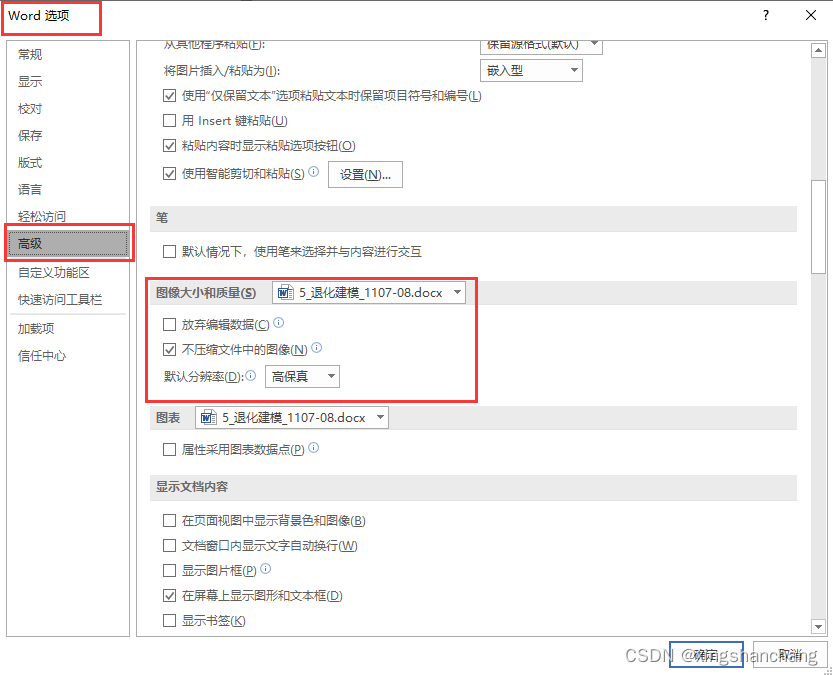
如何导出PPT画的图为高清图片?插入到world后不压缩图像的设置方法?
期刊投稿的时候,需要图片保持一定的清晰度数,那么我们怎么才能从PPT中导出符合要求的图片呢? 对于矢量图绘图软件所画的图,直接导出即可。 而PPT导出的图片清晰度在60pi,就很模糊。 整体思路: PPT绘图——…...

【Spring】Spring IOC DI
Spring IOC & DI IOC DI入门什么是Spring什么是容器什么是IOC IOC介绍传统程序开发解决方案 DI IOC详解Bean的存储Controller(控制器存储)Service(服务存储)Repository(仓库存储)Component(组件存储)Configuration(配置存储) 为什么需要这么多类注解类注解之间的关系方法注…...
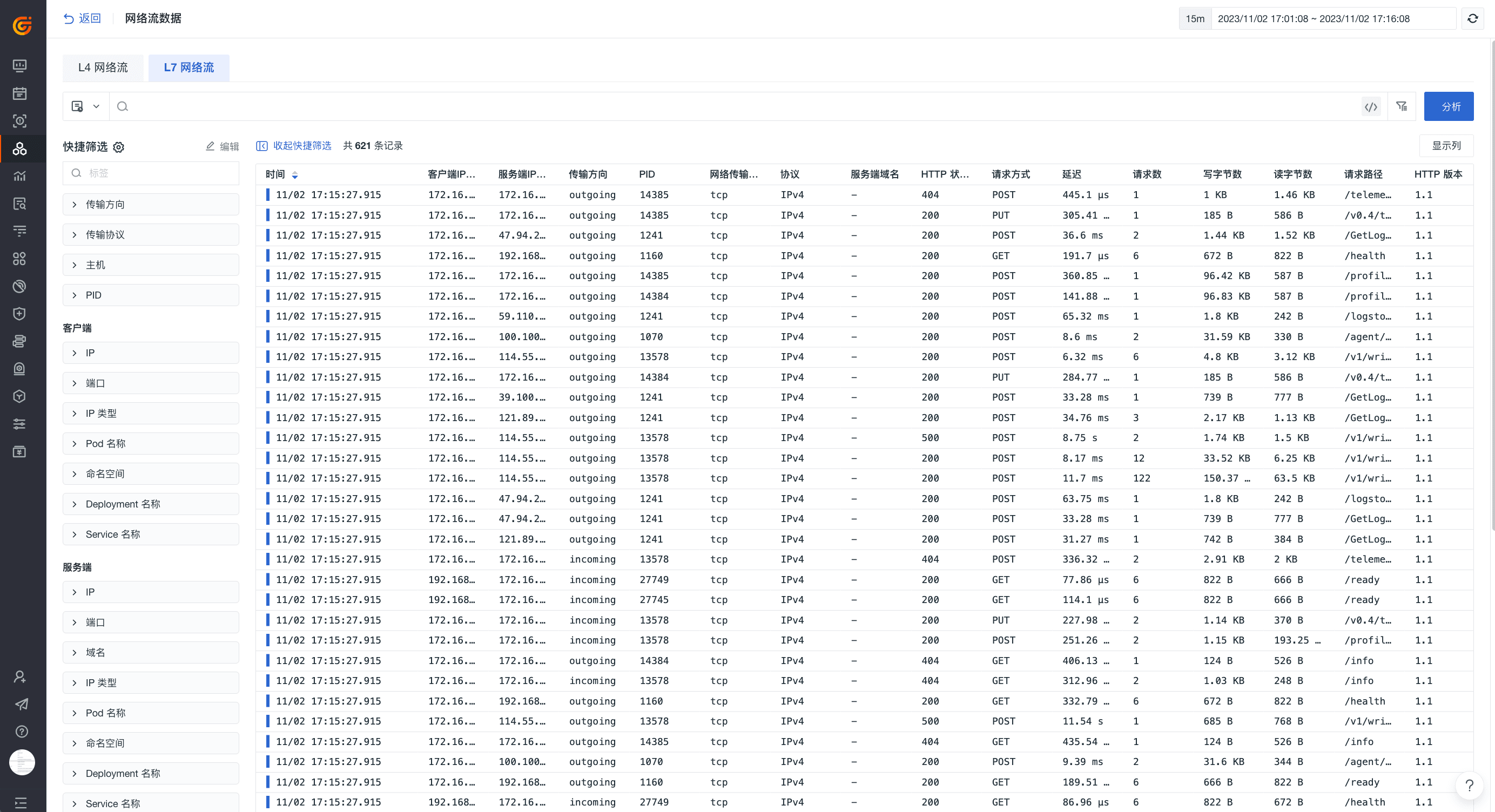
一招解密网络流量瓶颈!
前言 我们曾介绍过观测云提供全面的基础设施监测方案(参见《全方位监控基础设施,坚实守护您的业务稳定!》),能够高效全面地帮助您实时观测所有的基础设施对象及云产品等,赋能您的业务稳定发展。今天我们将…...

某校帮签到小程序m 加密参数解析
小程序解密清参考我以前的文章 VX小程序逆向 js版本 function n(e, a) {var t (65535 & e) (65535 & a);return (e >> 16) (a >> 16) (t >> 16) << 16 | 65535 & t };function i(e, a, t, n, r, i, s) {return o(a & n | t &…...
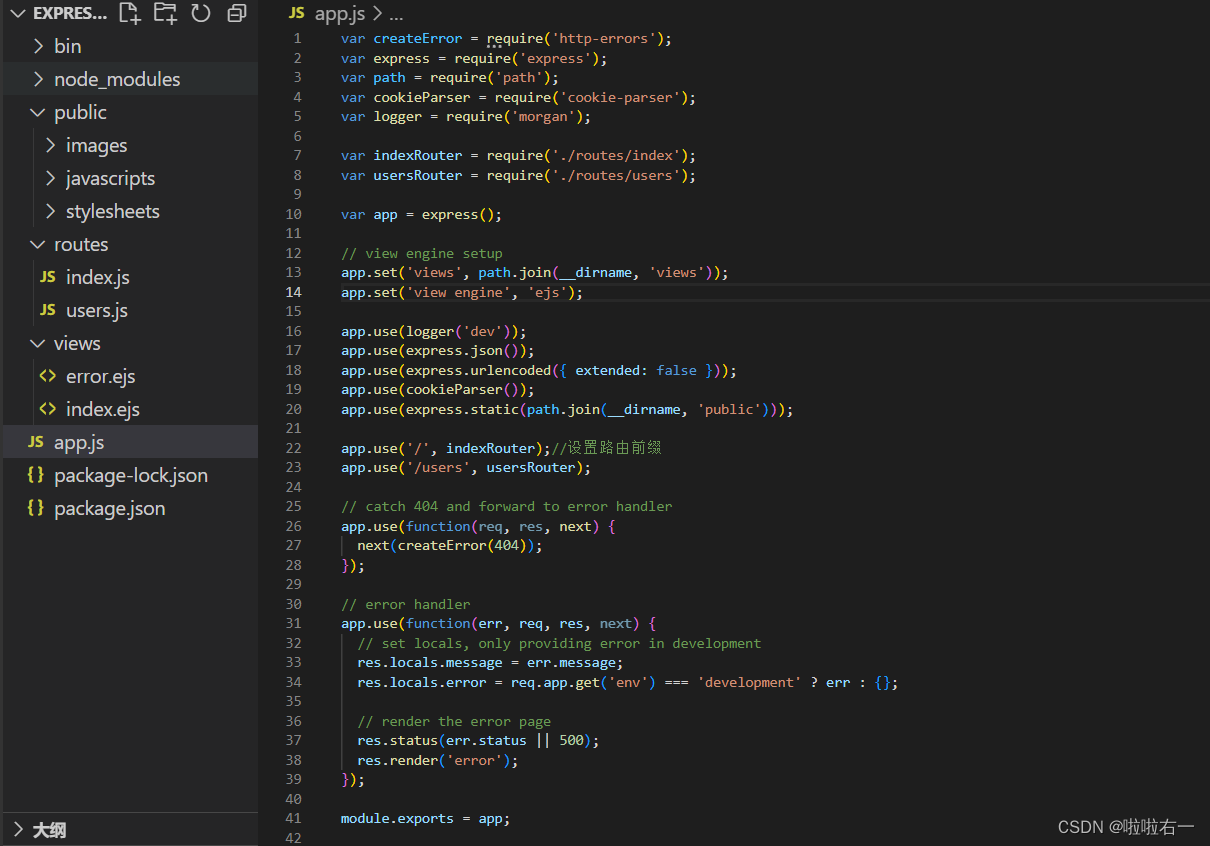
Node.js |(六)express框架 | 尚硅谷2023版Node.js零基础视频教程
学习视频:尚硅谷2023版Node.js零基础视频教程,nodejs新手到高手 文章目录 📚express使用🐇初体验🐇express路由⭐️路由的使用⭐️获取请求参数⭐️获取路由参数🔥练习:根据路由参数响应歌手信息…...

包教包会:Mysql主从复制搭建
笑小枫的专属目录 一、无聊的理论知识1. 主从复制原理2. 主从复制的工作过程3. MySQL四种同步方式 二、docker下安装、启动mysql1. 安装主库2. 安装从库 三、配置Master(主)四、配置Slave(从)五、链接Master(主)和Slave(从)六、主从复制排错1. 错误:error connectin…...

Subset Selection
白话解释:https://www.geeksforgeeks.org/feature-subset-selection-process/ 貌似有一种比较常见的方法,称为多元逐步回归有3种筛选自变量的方法 (1)向前法:n个因变量情况,慢慢增加因变量到方程中&#x…...

【测开求职】面试题:计算机网络 精简版整理
本篇文章整理的是在秋招过程中遇到的计算机网络高频面试题,应付部分中小厂的测试开发工程师面试完全没有问题,如果时间充足的话,建议再看一下笔者的另外一篇文章:【测开求职】面试题:计算机网络 详细版整理,会让你对整个计算机网络有足够全面深刻的理解,亲测应付各个大厂…...
)
设计模式-代理模式(delegate)
什么是代理? 代理(Proxy)是一种设计模式,提供了对目标对象另外的访问方式;即通过代理对象访问目标对象.这样做的好处是:可以在目标对象实现的基础上,增强额外的功能操作,即扩展目标对象的功能. 这里使用到编程中的一个思想:不要随意去修改别人已经写好的代码或者方…...

MongoDB 安装与配置
MongoDB 安装与配置 MongoDB 是一个高性能、开源的 NoSQL 数据库,它提供了丰富的查询功能和高可用性。本文将详细讲解 MongoDB 的安装与配置过程。 1. MongoDB 安装 1.1 Windows 平台安装 下载 MongoDB 安装包 访问 MongoDB 官方下载页面(https://w…...
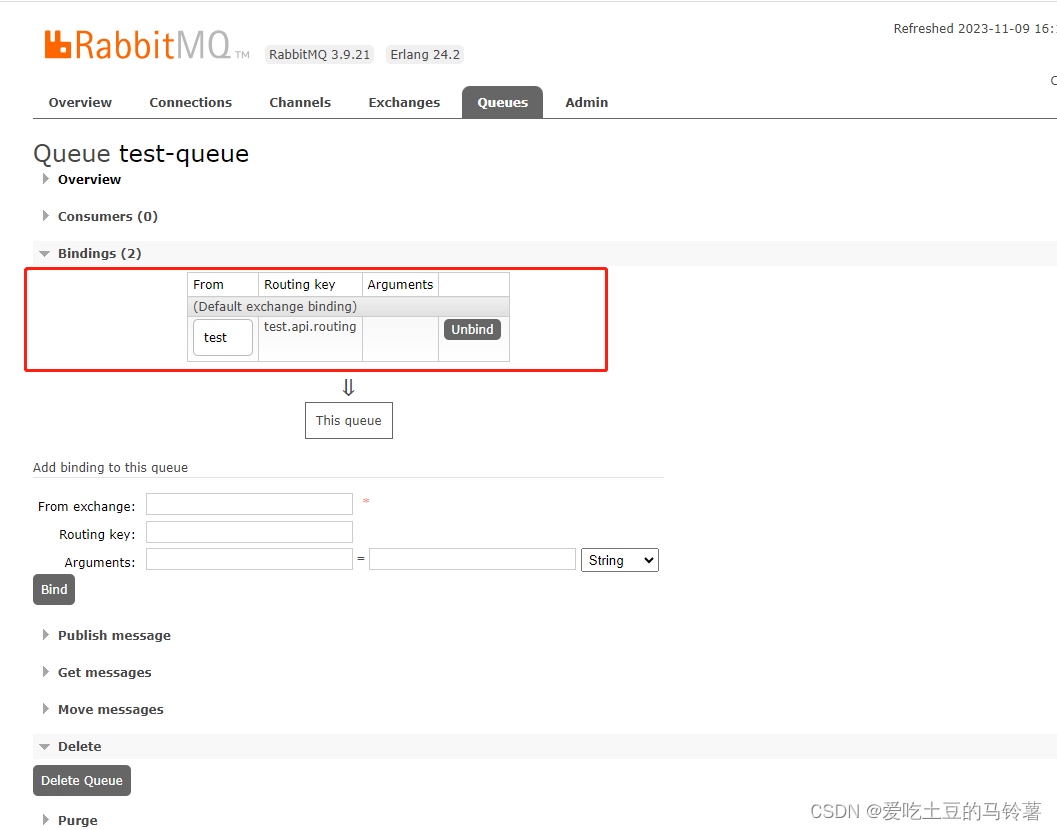
rabbitMq创建交换机,以及路由键绑定队列教程
创建交换机: 创建队列: 创建路由,绑定到交换机:...

odoo16前端框架源码阅读——ormService.js
odoo16前端框架源码阅读——ormService.js 路径:addons\web\static\src\core\orm_service.js 简单翻译一下代码中的注释: ORM服务是js代码和python的ORM层通信的标准方法。 然后讲了One2many and Many2many特使的指令格式,每个指令都是3元…...

详谈滑动窗口算法与KMP算法区别以及二者在什么场景下使用
什么是滑动窗口算法 滑动窗口算法是一种用于解决数组(或字符串)中子数组(或子字符串)问题的算法。该算法通过维护一个固定大小的窗口(通常是两个指针),该窗口在数组上滑动,以寻找符…...

k8s、数据存储
数据存储的概念 容器磁盘上的文件的生命周期是短暂的,这就使得在容器中运行重要应用时会出现一些问题。首先,当容器崩溃时,kubelet 会重启它,但是容器中的文件将丢失——容器以干净的状态(镜像最初的状态)…...

Vue生命周期全解析:从工厂岗位到任务执行,一览无遗!
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、生…...
常见产品结构四大类型 优劣势比较
一般,我们通过产品架构来构建用户体验,这样可以提供更清晰的导航和组织、优化用户流程和交互、增强产品的可扩展性和可维护性,提升用户的满意度和忠诚度。如果没有明确的产品结构,可能会导致功能冗余或功能缺失、交互流程混乱等问…...
如何优雅的开发?试试这个低代码项目
一、前言 众所周知,开发一个大型的企业级系统,公司往往需要大量的人力做支持后盾,如需要需求分析师、数据库管理员、前台美工、后台程序员、测试人员等。 在快速发展中的企业里,尤其是中小企业,都是一个萝卜多个坑&…...

个人开发常用idea插件
idea重装后必须要配置的几项: Maven: File-->Settings-->Maven字体: IDE字体设置:File-->Settings-->Appearance,设置成Consolas,Size:18代码字体设置:File-->Setti…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...
