【经验模态分解】4.信号由时域向频域的转换
/*** @poject 经验模态分解及其衍生算法的研究及其在语音信号处理中的应用* @file 傅里叶变换与小波变换* @author jUicE_g2R(qq:3406291309)* * @language MATLAB* @EDA Base on matlabR2022b* @editor Obsidian(黑曜石笔记软件)* * @copyright 2023* @COPYRIGHT 原创学习笔记:转载需获得博主本人同意,且需标明转载源*/
- E M D EMD EMD 是 基于 傅里叶变换 与 小波变换 的改进
- E M D EMD EMD 与 离散小波变换 产生的背景是 基于解决 傅里叶变换 与 小波变换 在 时间尺度 上存在的缺陷
文章目录
- 1 傅里叶变换与短时傅里叶变换
- 1-1 (传统的)傅里叶变换
- 1-1-1 优点
- 1-1-2 缺陷
- 1-2 短时傅里叶变换
- 1-3 信号的频谱图和时频图实验
- 1-3-1 打开 信号分析器APP
- 1-3-2 面板设置
- 1-3-3 拖入信号
- 1-3-4 设置 采样率 S a m p l e R a t e SampleRate SampleRate
- 1-3-5 对每个面板选中相应的信号
- 1-3-6 选中面板并点击上方工具栏的**频谱**获得相应的频谱图
- 1-3-7 结论
- 2 离散小波变换
- 2-1 尺度因子
- 2-2 平移因子
1 傅里叶变换与短时傅里叶变换
1-1 (传统的)傅里叶变换
- 傅里叶变换(Fourier Transform)是一种将 时域上的信号转换到频域上 的数学工具
1-1-1 优点
| 优点 | 详细说明 |
|---|---|
| 可时频转换 | 傅里叶变换可以将时域上的信号转换为频域上的信号,便于对信号的频率特征进行分析和处理 |
| 可分解 | 傅里叶变换可以将信号分解成多个不同频率的正弦和余弦函数,这些分量可以提供有关信号频率和振幅的信息 |
| 线性性 | 傅里叶变换具有线性性,可以对多个信号进行叠加处理 |
| 可逆性 | 可以将频率域上的信号转换回时域上的信号 |
1-1-2 缺陷
| 缺陷 | 详细说明 |
|---|---|
| 实时性差 | 傅里叶变换是一种理论分析工具,不适合对信号进行实时处理,因此需要使用快速傅里叶变换(FFT)等算法来加速计算 |
| 普适性差 | 傅里叶变换需要将整个信号在时间上进行全局分析,计算复杂度较高,不适合对长时间信号进行处理 |
| 局部性差 | 傅里叶变换对信号的局部特征无法进行分析,对于非周期性信号和突发性信号的频谱分析效果较差 |
| 处理特殊情况效果差 | 傅里叶变换对于非线性信号、带噪声信号等情况处理效果较差 |
- 傅里叶变换 是 对 一段信号 不分时间先后 来观察其中的频率成分 及 各个频率成分的贡献,即没有时间分辨率(不可通过傅里叶变换知道一个特定时间点的频率成分)
1-2 短时傅里叶变换
- 短时傅里叶变换 是 基于 (传统的)傅里叶变换 中 时间分辨率的缺陷 给出了相应的改进方法
短时:即将 长段信号源 拆分成 多段 短的信号源(但是 窗口大小是固定的【固定窗长】,这也是它的缺陷)
Ts = 0:0.001:2; % 采样频率1000次每秒,时长为2s
%% 两个源信号用的是扫频函数chirp()
Sig_Low2High = chirp(Ts, 50, 2, 300); % 低频到高频:从 50Hz 线性升至 300Hz
Sig_High2Low = chirp(Ts, 300, 2, 50); % 高频到地频:从 300Hz 线性升至 50Hz
1-3 信号的频谱图和时频图实验
步骤:
1-3-1 打开 信号分析器APP

1-3-2 面板设置

1-3-3 拖入信号

1-3-4 设置 采样率 S a m p l e R a t e SampleRate SampleRate

注:两个信号要分别修改对应的 S a m p l e R a t e SampleRate SampleRate
1-3-5 对每个面板选中相应的信号

1-3-6 选中面板并点击上方工具栏的频谱获得相应的频谱图

-
分析上述频谱图
左面板是 高频 到 低频,右面板是 低频 到 高频:
两边的频谱图是一模一样的,一个原因是两个信号都是扫频函数(频率线性变化),另一个是频谱工具箱得到的频谱图是通过 傅里叶变换 得到的(傅里叶变换是全局的,两个全局确实一样,但局部不一样) -
选中面板并点击上方工具栏的时谱获得相应的时谱图

时频图是根据 短时傅里叶变换 得到的,很明显的可以看到两个信号的区别,同时体现了 短时傅里叶变换 具有 时间与频率的分辨率。
1-3-7 结论
傅里叶变换 相较于 短时傅里叶变换 存在明显的 时频分辨率 上的差异
2 离散小波变换
- 在 频域 上来看,离散小波变换 相当于一个 带通滤波器,相当于通过 尺度因子 与 平移因子
| 因子 | 作用 |
|---|---|
| 尺度因子 | 控制 小波基 的 伸展程度(控制 频率) |
| 平移因子 | 控制 时间 |
- 较 短时傅里叶变换 而言,离散小波变换 具有平衡 频率分辨率 与 时间分辨率 的优势
2-1 尺度因子
- 小波母函数
C e n t F r e q ( 中心频率 ) = S c a l e F a c t o r ( 尺度因子 ) ∗ f CentFreq(中心频率)=ScaleFactor(尺度因子)*f CentFreq(中心频率)=ScaleFactor(尺度因子)∗f
2-2 平移因子
-
能使得 时间和频率之间 达到 平衡
离散小波变换 是 对 短时傅里叶变换 在 固定窗长 这一特性出现 “低频精度不高,高频分辨率太低” 缺陷的一种解决办法。 -
C ( 常数 ) = W d n L e n ( 窗长 ) ∗ f C(常数)=WdnLen(窗长)*f C(常数)=WdnLen(窗长)∗f
高频时:具有很高的 时间分辨率,窗长小
低频时:具有很高的 频率精度,窗长大
本节参考视频源:NO.11 两步搞定经验模态分解与离散小波变换-哔哩哔哩
相关文章:

【经验模态分解】4.信号由时域向频域的转换
/*** poject 经验模态分解及其衍生算法的研究及其在语音信号处理中的应用* file 傅里叶变换与小波变换* author jUicE_g2R(qq:3406291309)* * language MATLAB* EDA Base on matlabR2022b* editor Obsidian(黑曜石笔记软件&#…...

STM32的M4内核在keil上面float访问就hard_fault原因
使用 Keil MDK(Microcontroller Development Kit)开发时,出现硬件故障(hard fault)通常是由于访问浮点数(float)数据类型时,浮点单元配置不正确或浮点单元启用导致的。以下是一些可能…...

【LeetCode】217. 存在重复元素
217. 存在重复元素 难度:简单 题目 给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。 示例 1: 输入:nums [1,2,3,1] 输出࿱…...
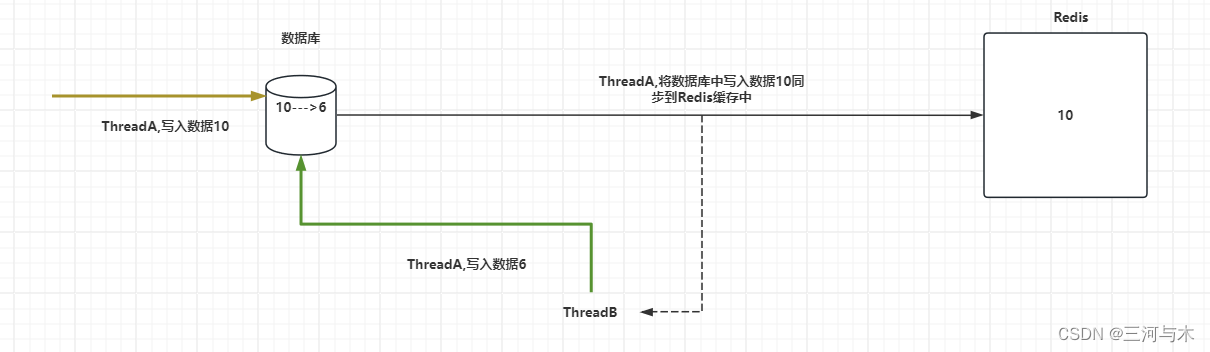
【Redis缓存架构实战常见问题剖析】
文章目录 一、Redis缓存架构实战剖析1.1、大规模的商品缓存数据冷热分离机制1.2、缓存击穿导致线上数据压力暴增解决方案1.3、缓存穿透及其解决方案剖析1.4、突发性的热点缓存数重建导致系统压力暴增问题分析1.5、Redis分布式锁解决缓存与数据库双写不一致问题剖析1.6、利用多级…...
mac M2 pytorch_geometric安装
我目前的环境是mac M2,我在base环境中安装了pytorch_geometric,仅仅做测试用的,不做真正跑代码的测试 首先我的base环境的设置如下: pip install pyg_lib torch_scatter torch_sparse torch_cluster torch_spline_conv -f https://data.pyg.…...
【C++】异常 智能指针
C异常 & 智能指针 1.C异常1.1.异常的抛出与捕获1.2.异常体系1.3.异常安全与规范1.4.异常优缺点 2.智能指针2.1.RAII2.2.智能指针的使用及原理2.2.1.auto_ptr2.2.2.unique_ptr2.2.3.shared_ptr2.2.4.shared_ptr的循环引用问题 & weak_ptr 2.3.定制删除器 1.C异常 C异常…...

切换数据库的临时表空间为temp1 / 切换数据库的undo表空间为 undotbs01
目录 编辑 一、切换临时表空间 1、登录数据库 2、查询默认临时表空间 3、创建临时表空间temp1(我们的目标表空间) 4、修改默认temp表空间 5、查询用户默认临时表空间 6、命令总结: 二、切换数据库的undo表空间 1、查询默认undo表…...

react: scss使用样式
方式一: 将样式作为模块使用 //List.tsx import styles from /styles/apppublish.module.scss <div className{styles.contentOverflow}></div>//apppublish.module.scss .contentOverflow {height: 100%;overflow-y: auto;display: flex;flex-directi…...

JAVA深化篇_36—— Java网络编程中的常用类
Java网络编程中的常用类 Java为了跨平台,在网络应用通信时是不允许直接调用操作系统接口的,而是由java.net包来提供网络功能。下面我们来介绍几个java.net包中的常用的类。 InetAddress的使用 作用:封装计算机的IP地址和DNS(没…...

python操作链接数据库和Mysql中的事务在python的处理
python操作数据库 pymysql模块: pip install pymysql作用:可以实现使用python程序链接mysql数据库,且可以直接在python中执行sql语句 添加操作 import pymysql #1.创建链接对象c conn pymysql.Connect(host127.0.0.1,#数据库服务器主机地址port3306, #mysql的端口…...
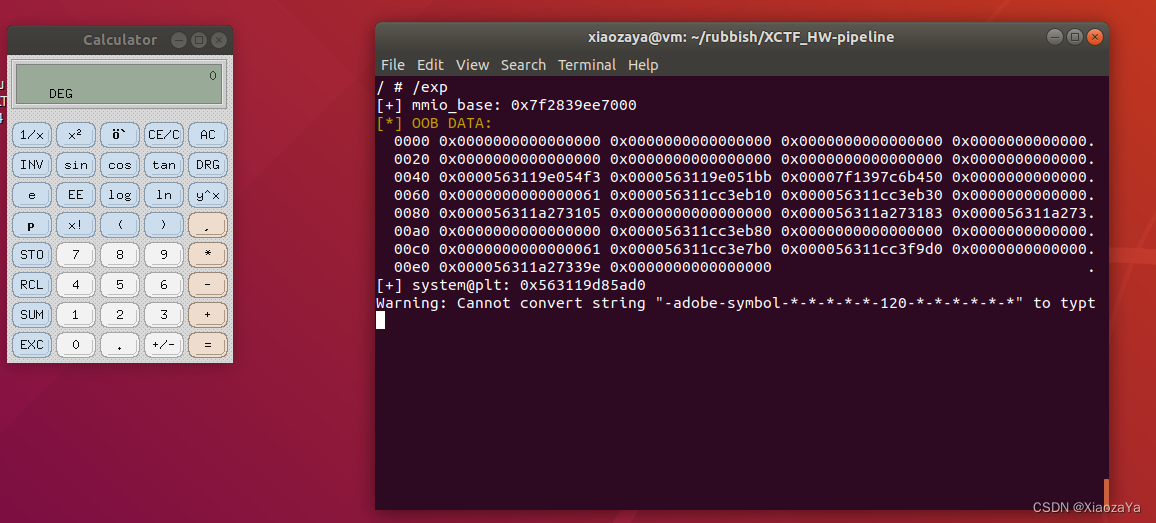
【qemu逃逸】XCTF 华为高校挑战赛决赛-pipeline
前言 虚拟机用户名: root 无密码 设备逆向与漏洞分析 程序没有去符合, 还是比较简单. 实例结构体如下: 先总体说一下流程: encode 为 base64 编码函数, decode 为 base64 解码函数. 然后 encPipe 和 decPipe 分别存放编码数据和解码数据, 分别有四个: 其中 EncPipeLine 中…...
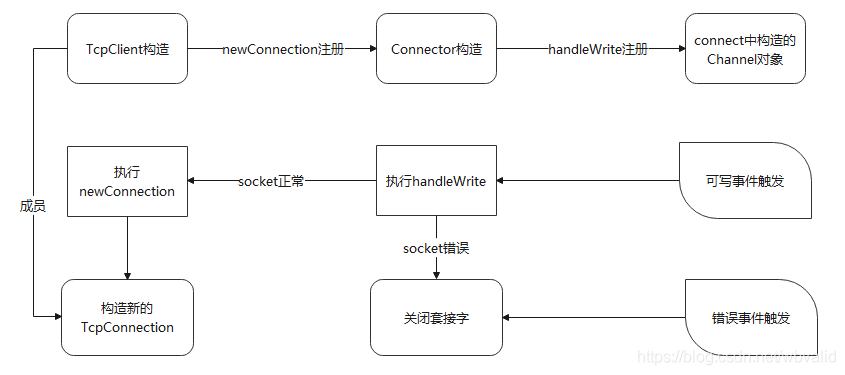
muduo源码剖析之TcpClient客户端类
简介 muduo用TcpClient发起连接,TcpClient有一个Connector连接器,TCPClient使用Conneccor发起连接, 连接建立成功后, 用socket创建TcpConnection来管理连接, 每个TcpClient class只管理一个TcpConnecction,连接建立成功后设置相应的回调函数…...
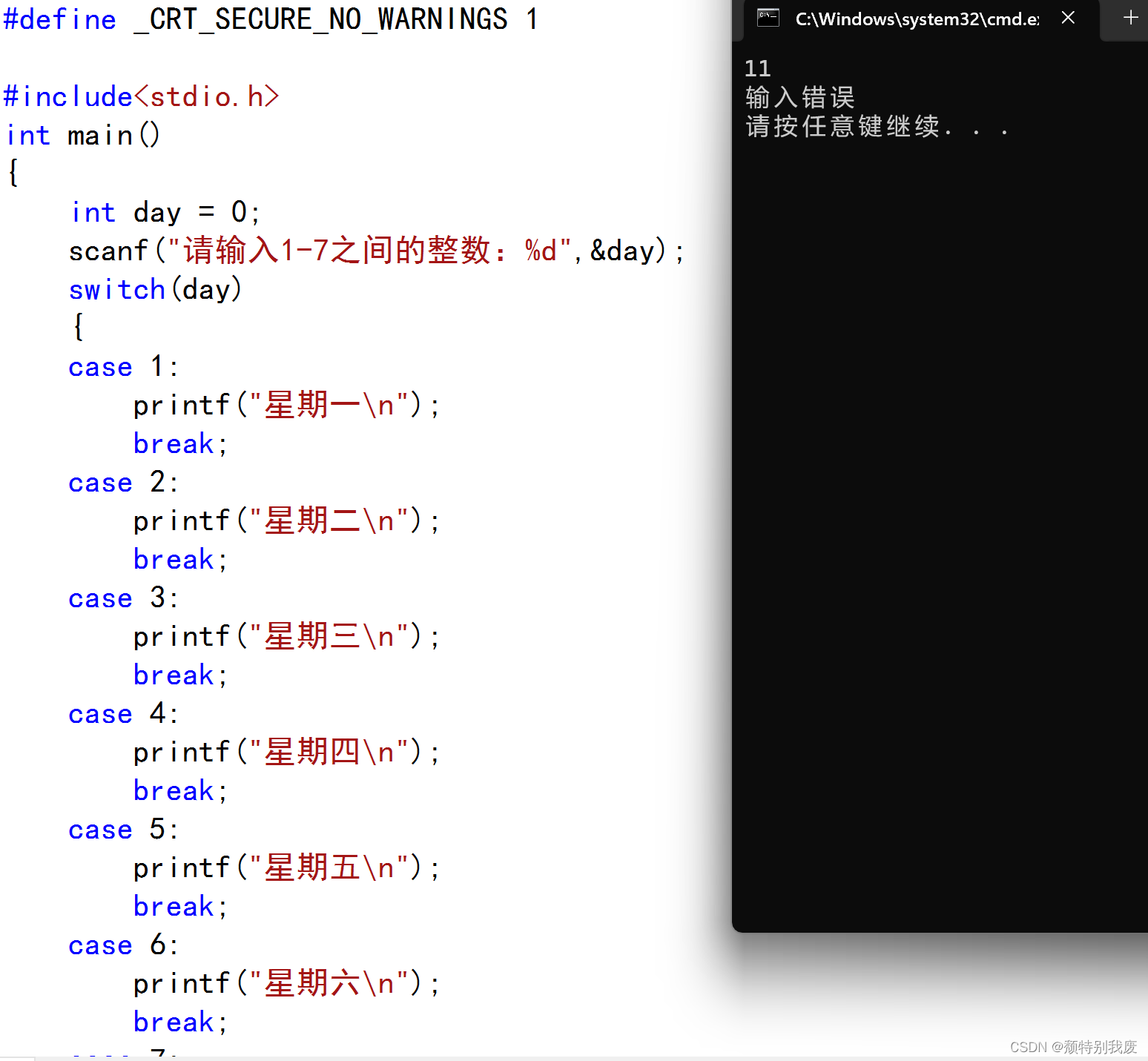
C语言——switch语句判断星期
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int main() {int day 0;scanf("请输入1-7之间的整数:%d",&day);switch(day){case 1:printf("星期一\n");break;case 2:printf("星期二\n");break;case 3:printf(&quo…...

栈回溯之CmBacktrace
简介 CmBacktrace (Cortex Microcontroller Backtrace)是一款针对 ARM Cortex-M 系列 MCU 的错误代码自动追踪、定位,错误原因自动分析的开源库。主要特性如下: 支持的错误包括: 断言(assert)…...
——MongoDB的基本命令)
node插件MongoDB(二)——MongoDB的基本命令
文章目录 前言1. 数据库命令(1)显示所有数据库(2)切换指定数据库(若没有自动创建)(3)显示当前所在数据库(4)删除当前数据库 2.集合(表名ÿ…...
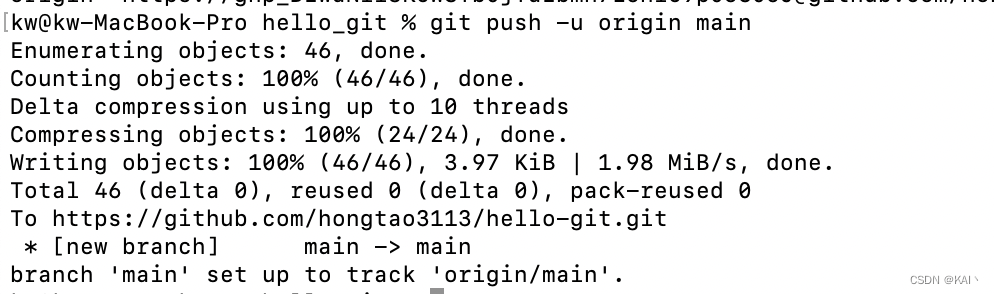
【Git】推送Github失败:remote: Permission to xxx/*.git denied to xxx
在github上,创建了token,推送代码报没权限 #设置token git remote set-url origin <your.token>github.com/<your.name>/hello-git.git#推送代码 #git push -u origin main remote: Permission to xxx/hello-git.git denied to xxx. fatal:…...
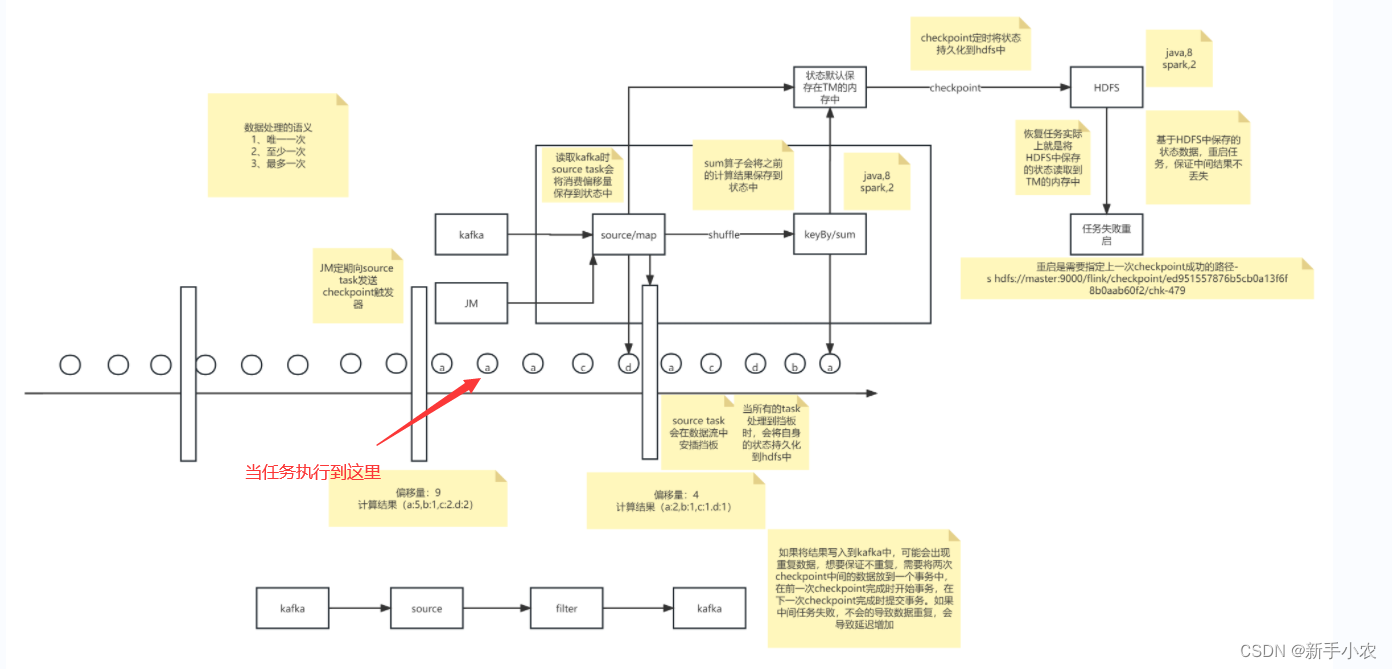
Flink -- 状态与容错
1、Stateful Operations 有状态算子: 有状态计算,使用到前面的数据,常见的有状态的算子:例如sum、reduce,因为它们在计算的时候都是用到了前面的计算的结果 总结来说,有状态计算并不是独立存在的…...
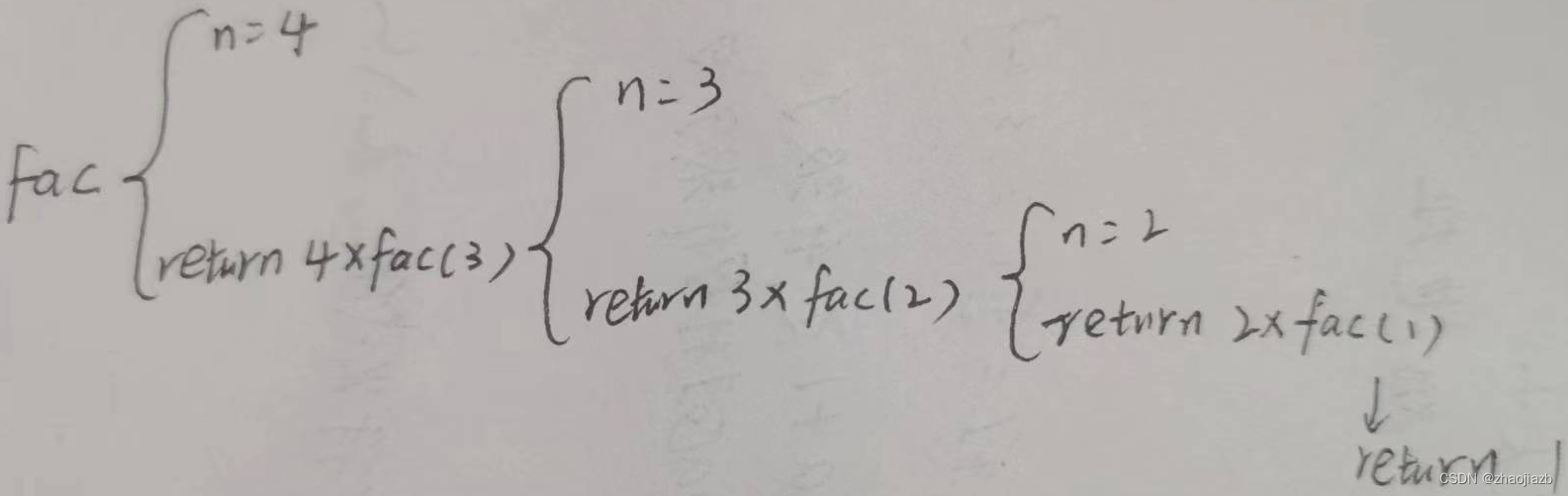
Linux C语言进阶-D15递归函数和函数指针
递归函数 指一个函数的函数体中直接或间接调用了该函数本身 执行过程分为两个过程: 递推过程:从原问题出发,按递归公式递推从未知到已知,最终达到递推终止条件 回归阶段:按递归终止条件求出结果,逆向逐步…...

LeetCode算法心得——全排列(回溯型排列)
大家好,我是晴天学长,排列型的回溯,需要的小伙伴可以关注支持一下哦!后续会继续更新的。💪💪💪 1) .全排列 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按…...

读取W25Q64的设备ID时输出0xff
发现的问题 读取W25Q64的设备ID时输出0xff 找到的不同解决方法 检查MISO和MOSI是否接对。MISO->DO,MOSI->DI检查程序在初始化spi时是否将SS拉高、SCK拉低如果是硬件spi那么检查SPI的初始化函数中,时钟极性SPI_CPOL误选为SPI_CPOL_Low࿰…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
