P1547 [USACO05MAR] Out of Hay S 题解
文章目录
- 题目描述
- 输入格式
- 输出格式
- 样例
- 样例输入
- 样例输出
- 完整代码
题目描述
Bessie 计划调查 N N N( 2 ≤ N ≤ 2 000 2 \leq N \leq 2\,000 2≤N≤2000)个农场的干草情况,它从 1 1 1 号农场出发。农场之间总共有 M M M( 1 ≤ M ≤ 1 0 4 1 \leq M \leq 10^4 1≤M≤104)条双向道路,所有道路的总长度不超过 1 0 9 10^9 109。有些农场之间存在着多条道路,所有的农场之间都是连通的。
Bessie 希望计算出该图中最小生成树中的最长边的长度。
输入格式
第一行两个整数 N , M N,M N,M。
接下来 M M M 行,每行三个用空格隔开的整数 A i , B i , L i A_i,B_i,L_i Ai,Bi,Li,表示 A i , B i A_i,B_i Ai,Bi 之间有一条道路,长度为 L i L_i Li。
输出格式
一个整数,表示最小生成树中的最长边的长度。
样例
样例输入
3 3
1 2 23
2 3 1000
1 3 43
样例输出
43
完整代码
#include <bits/stdc++.h>
using namespace std;
struct node {int to, nxt, w;
} e[1000002];
int f[200002];
int find(int x) {if (x == f[x])return x;elsereturn f[x] = find(f[x]);
}
bool cmp(node x, node y) { return x.w < y.w; }
int main() {int n, m, cnt = -1;scanf("%d%d", &n, &m);for (int i = 1; i <= m; i++) scanf("%d%d%d", &e[i].to, &e[i].nxt, &e[i].w);sort(e + 1, e + m + 1, cmp);for (int i = 1; i <= n; i++) f[i] = i;for (int i = 1; i <= m; i++) {int k = find(e[i].to), l = find(e[i].nxt);if (k != l)f[k] = l, cnt = max(cnt, e[i].w);}printf("%d", cnt);return 0;
}

相关文章:

P1547 [USACO05MAR] Out of Hay S 题解
文章目录 题目描述输入格式输出格式样例样例输入样例输出 完整代码 题目描述 Bessie 计划调查 N N N( 2 ≤ N ≤ 2 000 2 \leq N \leq 2\,000 2≤N≤2000)个农场的干草情况,它从 1 1 1 号农场出发。农场之间总共有 M M M( 1 ≤…...

2023.11.10联测总结
T 1 T1 T1求的是有多少个区间的异或和是 k k k的因子, n , k ≤ 1 0 5 n,k \leq 10^5 n,k≤105。 这道题用前缀和维护一下,暴力枚举所有区间就有 80 80 80分。 有一瞬间想过枚举因数,但是脑抽以为要 O ( n ) \mathcal O(n) O(n)枚举&#x…...

C++:list?自己模拟实现!
目录 1.list的模拟实现 1.1 成员变量和节点 1.2 迭代器实现 1.2.1 非const的迭代器 1.2.2 const的迭代器 1.2.3 一个模板实现 const 与 非const 迭代器 1.3 增删改查的实现 1.4 拷贝构造函数,析构函数与赋值运算符重载 1.5 泛型编程实现打印 2. list 反…...
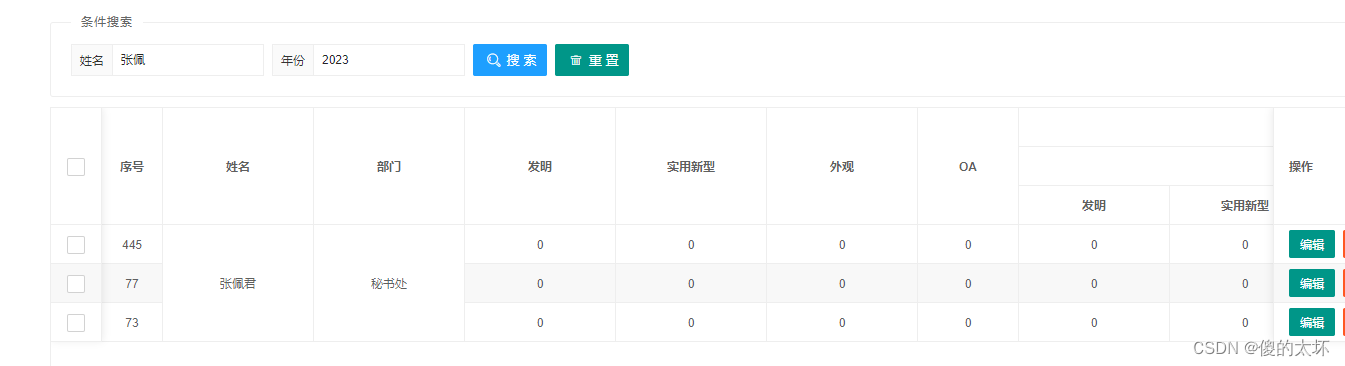
layui table合并相同的列
table.render({elem: #samples,url: /index/Develorderss/samplelists?od_idod_id //数据接口,page: { //支持传入 laypage 组件的所有参数(某些参数除外,如:jump/elem) - 详见文档layout: [prev, page, next, count,skip,limit]…...
【Spring】SpringBoot配置文件
SpringBoot配置文件 配置文件作用SpringBoot配置文件配置文件快速入手配置文件的格式properties配置文件说明基本语法读取配置文件properties缺点分析 yml配置文件说明yml基本语法yml使用进阶yml配置读取配置对象配置集合配置Mapyml优缺点 配置文件作用 计算机上有数以千计的配…...

python批量下载txt文件中链接的数据
python下载txt文件中链接的数据,以gimms ndvi3g下载为例 官方下载网址:https://www.ncei.noaa.gov/data/land-normalized-difference-vegetation-index/access/ 选择下载2020年数据为例: 网址:Index of /data/land-normalized-difference-vegetation-index/access/2020…...

stm32 Bootloader设计(YModem协议)
stm32 Bootloader设计(YModem协议) Chapter1 stm32 Bootloader设计(YModem协议)YModem协议:STM32 Bootloader软件设计STM32 Bootloader使用方法准备工作stm32 Bootloader修改:stm32目标板程序.bin偏移地址修改: Chapt…...

竞赛 题目: 基于深度学习的疲劳驾驶检测 深度学习
文章目录 0 前言1 课题背景2 实现目标3 当前市面上疲劳驾驶检测的方法4 相关数据集5 基于头部姿态的驾驶疲劳检测5.1 如何确定疲劳状态5.2 算法步骤5.3 打瞌睡判断 6 基于CNN与SVM的疲劳检测方法6.1 网络结构6.2 疲劳图像分类训练6.3 训练结果 7 最后 0 前言 🔥 优…...
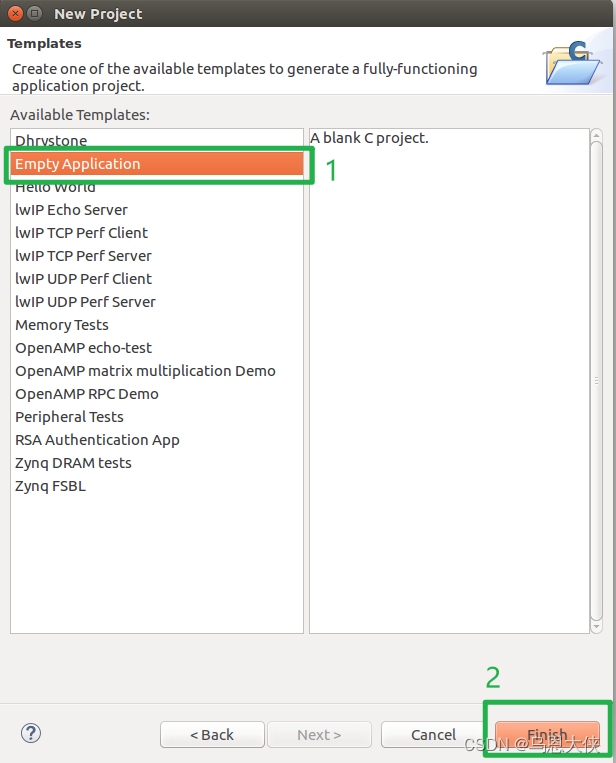
ubuntu 16.04.5 安装 vivado 2019.1 完整编译AD9361的环境
一、前期安装 1、安装ncurses库(已经包含了,其他的os需要安装) sudo apt install libncurses5二、安装 sudo ./xsetup使用lic进行激活。 三、安装后 输入指令 sudo gedit ~/.bashrc 末尾添加 source /opt/Xilinx/Vivado/2019.1/setti…...
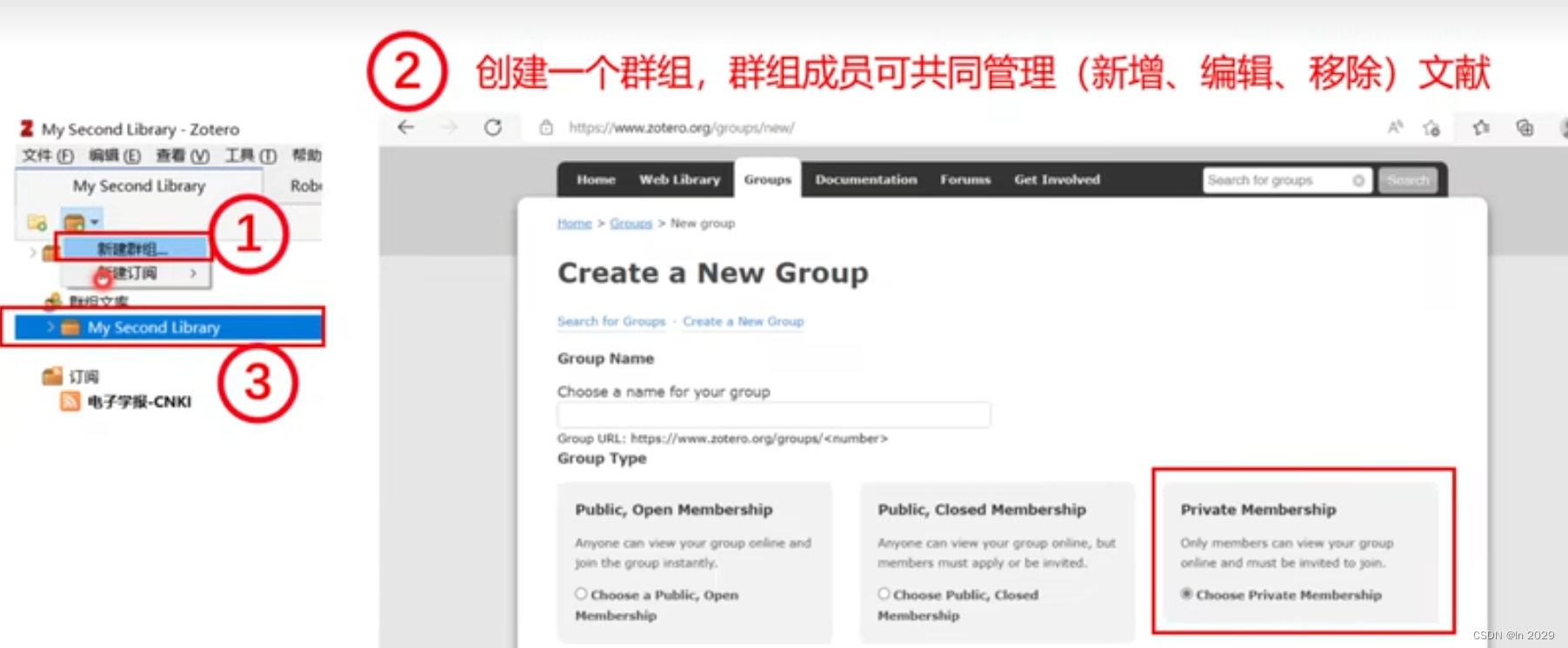
Zotero详细功能补充!熟练使用!【进阶版,持续更新】
Zotero安装请参见文章Zotero安装 1.改变条目文件夹 如果直接选择条目直接进行移动,能移动成功,但是原来文件夹和目标文件夹都会存在,实际是复制! 如果只想保留在一个文件夹里面,可以选中条目,右击-从分…...

【Windows】Windows系统常用命令大全
现实生活中,对电脑越熟悉懂得的快捷命令就越多。例如我们日常遇到的比较方便办公技巧,用快捷命令调用工具:调用计算器,Win键R,输入calc,回车,计算器界面弹出来; 调用记事本ÿ…...
大语言模型研究进展综述
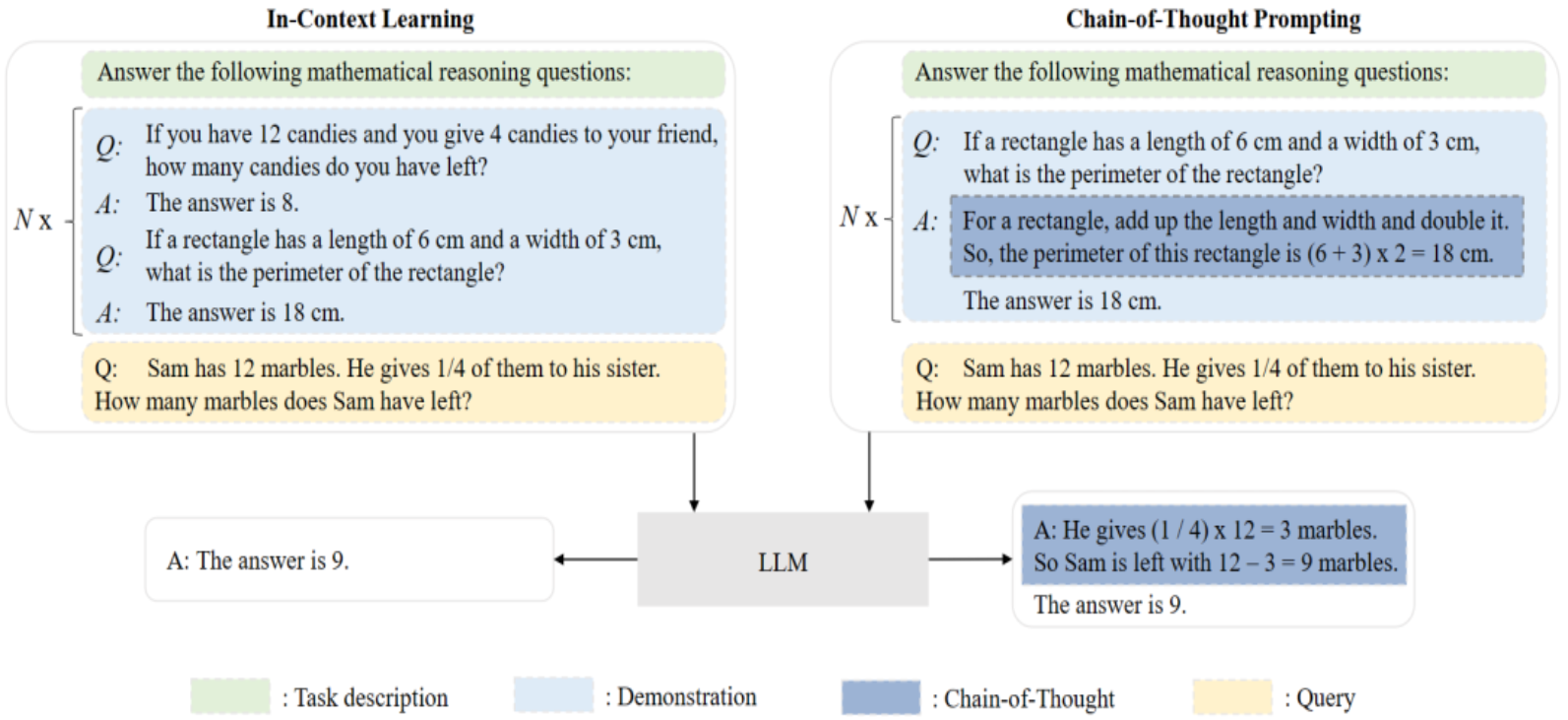
1、历史 自20世纪50年代图灵测试被提出以来,研究人员一直在探索和开发能够理解并掌握语言的人工智能技术。 作为重要的研究方向之一,语言模型得到了学术界的广泛研究,从早期的统计语言模型和神经语言模型开始,发展到基于Transform…...

linux gdb 调试 常见调试命令介绍+总结
1.调试前准备 -g gcc arcg.c -g -oO -o app //必须添加-g 2.调试 gdb gdb app 3.常见调试命令 set args 1 2 3 4 5 6 //设置参数 show args //查看参数 3.1执行程序 1.start2. run gdb app set args 1 2 3 4 5 start //执行一行 c //继续执行 q…...

基于JavaWeb+SSM+Vue微信小程序校园兼职任务平台系统的设计和实现
基于JavaWebSSMVue微信小程序校园兼职任务平台系统的设计和实现 源码传送入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码传送入口 前言 随着社会的发展和全球疫情的冲击,大学生的就业形势越来越严峻。越…...
)
我的MQTT操作类(M2Mqtt.Net)
类本体 4.3.0 public class MQTTMain{public MqttClient mqttClient null ; public bool MQTTMainConnect(string MenZuNo, string ServerIP, int ServerPort, string UserName, string Pwd){try{string EMQX_CLIENT_ID $"称重端-{MenZuNo}-{OPCommon.PCControl.G…...
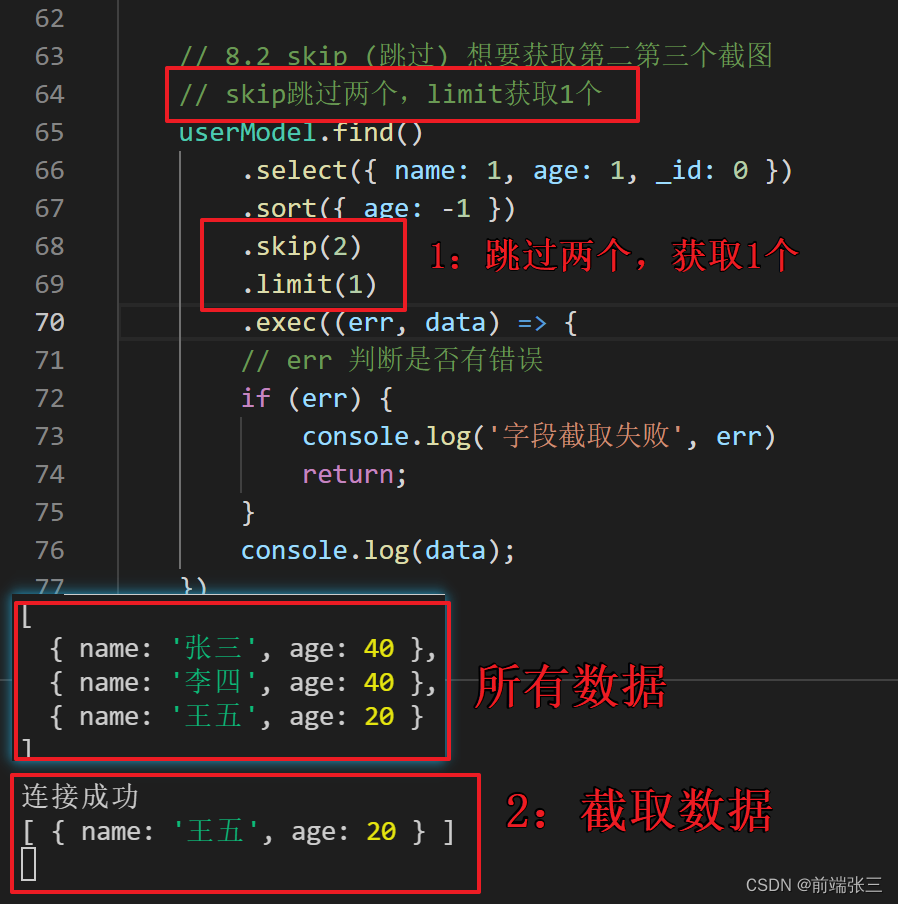
node插件MongoDB(四)—— 库mongoose 的个性话读取(字段筛选、数据排序、数据截取)(四)
文章目录 一、字段筛选二、数据排序三、数据截取1. skip 跳过2. limit 限定 一、字段筛选 字段筛选:只读取指定的数据,比如集合(表)中有…...

AI:73-结合语法知识的神经机器翻译研究
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...

[LeetCode]-225. 用队列实现栈
目录 225. 用队列实现栈 题目 思路 代码 225. 用队列实现栈 225. 用队列实现栈 - 力扣(LeetCode)https://leetcode.cn/problems/implement-stack-using-queues/description/ 题目 请你仅使用两个队列实现一个后入先出(LIFO࿰…...

Kafka Rebanlace次数过高问题
Kafka Rebanlace次数过高问题 环境: Kafka Server 2.6.x Kafka Client Java 2.8.2 缘起: 最近发现Kafka Rebalance次数着实有点多,一天达到了六十多次,感觉不太正常,于是查了下日志发现: Offset commit c…...

计算机是如何进行工作的+进程和线程
一)计算机是如何工作的? 指令是如何执行的?CPU基本工作过程? 假设上面有一些指令表,假设CPU上面有两个寄存器A的编号是00,B的编号是01 1)第一个指令0010 1010,这个指令的意思就是说把1010地址上面的数据给他读取到A寄存器里面 2…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
