网格变形算法
网格变形
- 需求分析
- 技术分析
需求分析
根据几何模型上的几个特征点,对几何模型进行变形。比如

技术分析
把几何模型使用三角面片表示,然后通过网格映射变形进行实现。关于网格这块有本经典的书可以参考,《ploygon mesh processing》。上面那个模型看着比较复杂,现在使用比较简单的模型来讲解一种映射方法。

如上图,为2D模型,左图为原始模型, P 1 \mathbf{P} _1 P1 , P 2 \mathbf{P} _2 P2 , P 3 \mathbf{P} _3 P3 , P o \mathbf{P} _o Po 坐标已知,右图为变形后模型,其中 P 11 \mathbf{P} _{11} P11 , P 12 \mathbf{P} _{12} P12 , P 13 \mathbf{P} _{13} P13 坐标已知,求 P 1 o \mathbf{P} _{1o} P1o 的坐标。将 P 1 o \mathbf{P} _{1o} P1o的坐标表示成 P 11 \mathbf{P} _{11} P11 , P 12 \mathbf{P} _{12} P12 , P 13 \mathbf{P} _{13} P13 的线性组合,比如 P o = k 1 P 1 + k 2 P 2 + k 3 P 3 \mathbf{P} _{o} = k_1\mathbf{P} _1 + k_2\mathbf{P} _2+k_3\mathbf{P} _3 Po=k1P1+k2P2+k3P3 ,因为是映射嘛,这里使用同样的系数 k \mathbf{k} k ,即 P 1 o = k 1 P 11 + k 2 P 12 + k 3 P 13 \mathbf{P} _{1o} = k_1\mathbf{P} _{11} + k_2\mathbf{P} _{12}+k_3\mathbf{P} _{13} P1o=k1P11+k2P12+k3P13 写成坐标的矩阵形式
[ P 1 x P 2 x P 3 x P 1 y P 2 y P 3 y ] [ k 1 k 2 k 3 ] = [ P o x P o y ] ( 1 ) \begin{bmatrix} P_{1x}&P_{2x}&P_{3x}\\ P_{1y}&P_{2y}&P_{3y} \end{bmatrix} \begin{bmatrix} k_{1}\\ k_{2}\\ k_{3} \end{bmatrix} =\begin{bmatrix} P_{ox}\\ P_{oy} \end{bmatrix} (1) [P1xP1yP2xP2yP3xP3y] k1k2k3 =[PoxPoy](1)
和
[ P 11 x P 12 x P 13 x P 11 y P 12 y P 13 y ] [ k 1 k 2 k 3 ] = [ P 1 o x P 1 o y ] ( 2 ) \begin{bmatrix} P_{11x}&P_{12x}&P_{13x}\\ P_{11y}&P_{12y}&P_{13y} \end{bmatrix} \begin{bmatrix} k_{1}\\ k_{2}\\ k_{3} \end{bmatrix} =\begin{bmatrix} P_{1ox}\\ P_{1oy} \end{bmatrix} (2) [P11xP11yP12xP12yP13xP13y] k1k2k3 =[P1oxP1oy](2)
如果能从(1)式中求出 k 1 {k} _{1} k1, k 2 {k} _{2} k2 , k 3 {k} _{3} k3然后带入(2)式,就可以算出待求点坐标了。至于如何从(1)式中求出 k 1 {k} _{1} k1, k 2 {k} _{2} k2 , k 3 {k} _{3} k3,其实是一个线性方程组求解问题, A m n X n = b A_{mn}X_{n}=b AmnXn=b
在三维空间里,m=3(也就是xyz三个分量),有几个特征点,n就等于几。因为不是方阵无法直接求逆,可以使用伪逆矩阵进行计算,只要解出一组解的k值,就是找到了一个点映射。其他的网格点依次执行就可以了。这样算出来的网格可能会畸变比较大,或者形状不理想现象。至于畸变大可以描述为不够平滑,仍然有很多数学工具可以使用,比如拉普拉斯平滑等。
相关文章:

网格变形算法
网格变形 需求分析技术分析 需求分析 根据几何模型上的几个特征点,对几何模型进行变形。比如 技术分析 把几何模型使用三角面片表示,然后通过网格映射变形进行实现。关于网格这块有本经典的书可以参考,《ploygon mesh processing》。上面…...

2. Spark报错,Task is Failed,errorMsg: FileNotFoundException xxxx
完整报错信息 21304, Task is Failed,errorMsg: FileNotFoundException: File does not exist: hdfs://xxxx-bigdata-nameservice/user/hive/warehouse/edw_ic.db/xxxx/part-00000-c8a718b3-54b3-42de-b36c-d6eedefd2e02-c000.snappy.parquet It is possible the xxx报错场景 …...

Flutter开发实战之上传身份照片并认证
思路 UI视图 上传身份证照片可以选择拍照方式上传,相册选择方式上传即可 身份证照片进行认证功能实现 对身份证照片进行认证,包括正面认证和反面认证即可上传给后端 使用第三方插件 image_picker: ^0.8.4Future<XFile> _getCameraImage() async {final cameraImages = …...

C++文件加密、解密
简介 在计算机科学中,密码学是一种通过编码和解码信息以保护数据安全的技术。C++作为一种通用编程语言,可用于实现各种密码学算法。本文将介绍如何使用C++对文件进行加密和解密。以下是使用C++进行文件加密的示例。 文件加密 在C++中,我们可以使用密码学中的异或(XOR)操作…...
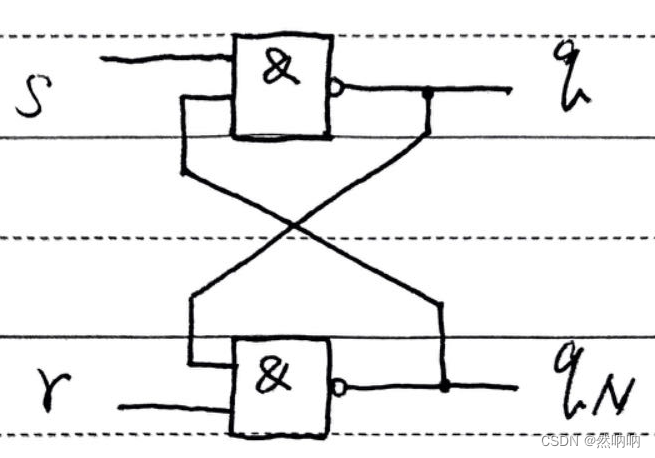
使用Java语言实现基本RS触发器
使用Java语言实现计算机程序来模拟基本RS触发器的工作过程,通过本账号2023年10月17日所发布博客“使用Java语言实现数字电路模拟器”中模拟基本逻辑门组成半加器电路的方法来模拟基本触发器的组成和时间延迟。 1 基本RS触发器电路结构 基本RS触发器(又…...

c++函数指针作为std::map值
遇见一个场景,收到的tcp消息有个OperationID,然后执行具体的任务(函数),在c#中使用Dictionary结合委托一点没问题,c#代码如下: public delegate void TcpHandler();Dictionary<OperateID, Tc…...
可以打印出来,不重新渲染)
data对象内新增属性,console.log()可以打印出来,不重新渲染
原因:受 ES5 的限制,Vue.js 不能检测到对象属性的添加或删除。因为 Vue.js 在初始化实例时将属性转为 getter/setter,所以属性必须在 data 对象上才能让 Vue.js 转换它,才能让它是响应的; data(){newTitle:{title:’…...

React:实现一个定时器计数器,每秒自动+1
需求:实现一个定时器计数器,每秒自动1 import React, { useState, useEffect } from "react";export default function App() {let [count, setCount] useState(0);useEffect(() > {let timer setInterval(() > {setCount(count 1);…...
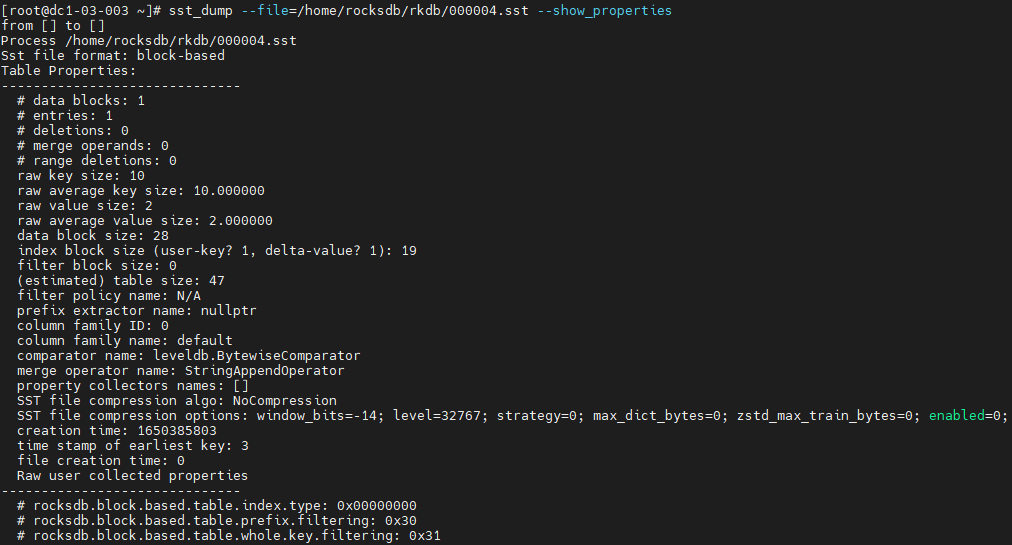
rocksdb 中 db_bench 的使用方法
硬件要求 硬件要求如表1所示。 表1 硬件要求 项目 说明 CPU 12 * AMD Ryzen 5 5500U with Radeon Graphics 内存 DDR4 磁盘 HDD 软件要求 软件要求如表2所示。 表2 软件要求 项目 版本 说明 下载地址 CentOS 7.6 操作系统。 Download kernel 4.14.0 内核。…...

【前端】TypeScript核心知识点讲解
1.TypeScript简介及入门案例 (1)什么是TypeScript? TypeScript 是 JavaScript 的一个超集,支持 ECMAScript 6 (ES6)标准。 TypeScript 由微软开发的自由和开源的编程语言。 TypeScript 设计目标是开发大…...
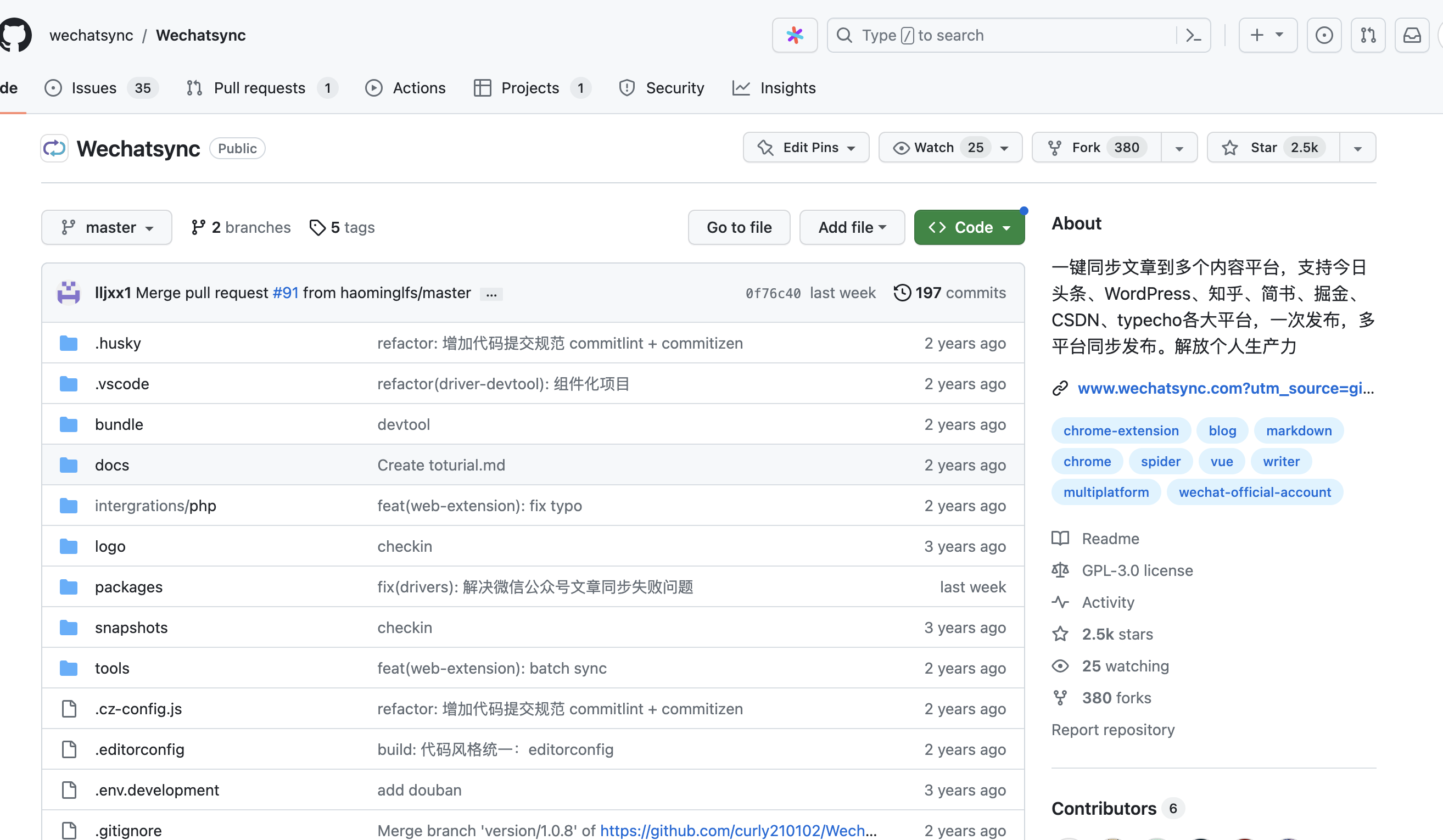
【工具推荐】一键多平台文章发布神器推荐(免费)
hello,大家好,我是你们老朋友洛林,上一篇文章说到自己深受多平台手动发布的折磨「传送门」,准备开发一款文章多平台工具,后来联系到 Wechatsync 原作者进行了简单的沟通,下面是关于以后的一些规划ÿ…...
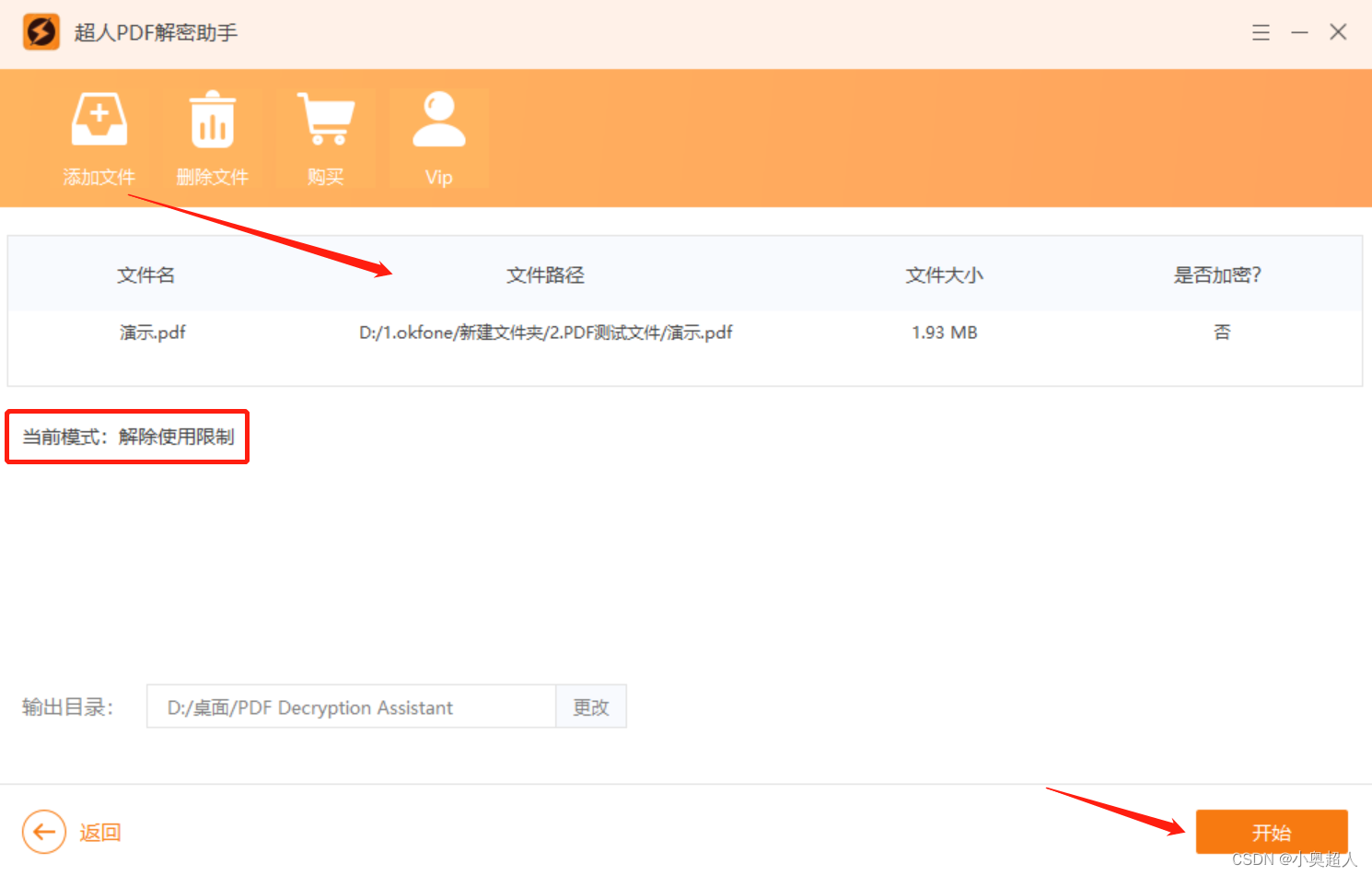
PDF有限制密码,不能复制怎么办?
大家现在接触PDF文件越来越多,有的时候在网上下载的PDF文件打开之后,发现选中文字之后无法复制。甚至其他功能也都无法使用,这是怎么回事?该怎么办? 当我们发现文件打开之后,编辑功能无法使用,很…...

【原创学位论文】基于python和定向爬虫的商品比价系统.docx
基于python和定向爬虫的商品比价系统 Price Comparison System for Products Based on Python and Targeted Web Crawling 目录 目录 2 摘要 3 关键词 3 第一章 绪论 4 1.1 研究背景 4 1.2 研究意义 5 1.3 国内外研究现状 7 1.4 本文主要工作和章节安排 8 第二章 Python基础…...

【Proteus仿真】【STM32单片机】汽车尾灯控制设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真STM32单片机控制器,使用按键、LED模块等。 主要功能: 系统运行后,系统运行后,系统开始运行,K1键控制左转向灯ÿ…...

多线程—锁
多线程中,锁用于确保同一时间只有一个线程可以访问共享资源,从而避免并发访问导致的数据不一致或者竞争条件等问题。 常见的锁有两种:互斥锁和读写锁。互斥锁的作用是保护共享资源,同时只允许一个线程访问,其他线程需…...
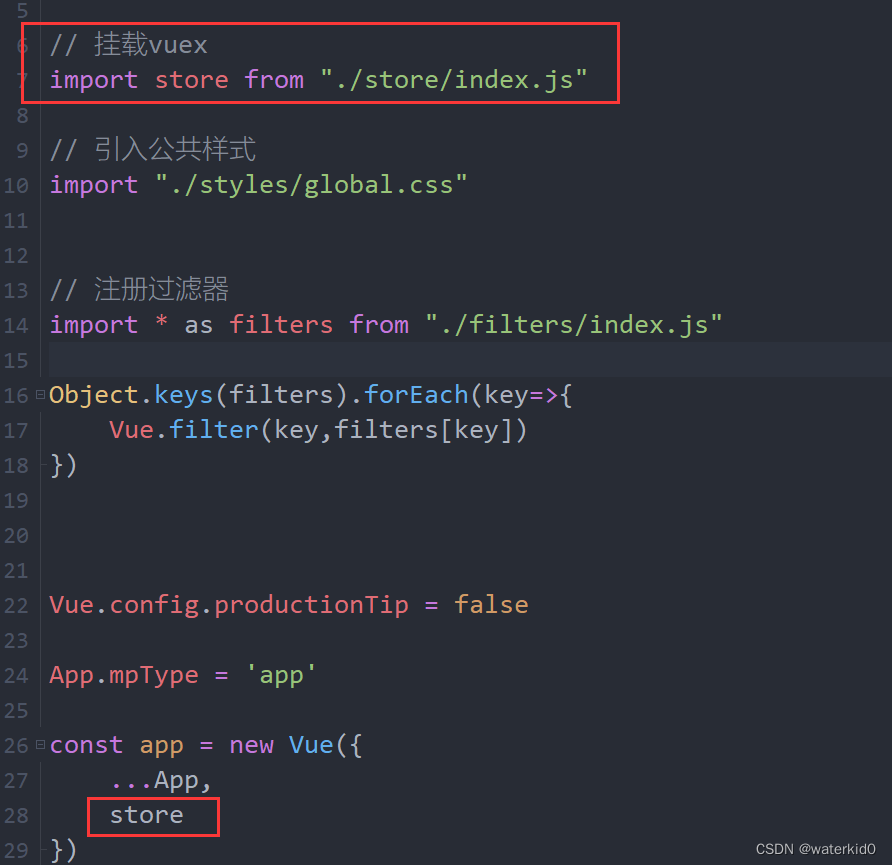
uniapp使用vue
uniapp集成了Vuex,,并不需要安装vuex 定义自己的vuex vuex中独立命名空间: 可以在模块中使用 namespaced 属性,设置为 true,,这样做的好处是,,不同模块之间的state,mut…...

能源监测管理系统有哪些作用与效果?
随着全球能源的不断增加,能源的有限性与环境问题日益严重,用能管理企业需要一种高效的方法来管理能源与利用能源,因此能源监测管理系统成为了一种不可或缺的工具。 能源监测管理系统的重要性 1、实现节能减排的目标 通过系统,可…...

数据分析是什么?
第一章- 数据分析是什么 数据分析是指 根据分析目的,用适当的分析方法及工具,对数据进行分析,提取有价值的信息,形成有效结论的过程。 数据分析的作用 通过观察数据,知道当前发生什么?通过具体的数据拆解…...
【kafka】Java客户端代码demo:自动异步提交、手动同步提交及提交颗粒度、动态负载均衡
一,代码及配置项介绍 kafka版本为3.6,部署在3台linux上。 maven依赖如下: <!-- kafka --><dependency><groupId>org.apache.kafka</groupId><artifactId>kafka_2.13</artifactId><version>3.6.0…...
【Git】Gui图形化管理、SSH协议私库集成IDEA使用
一、Gui图形化界面使用 1、根据自己需求打开管理器 2、克隆现有的库 3、图形化界面介绍 1、首先在本地仓库更新一个代码文件,进行使用: 2、进入图形管理界面刷新代码资源: 3、点击Stage changed 跟踪文件,将文件处于暂存区 4、通过…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
