【数据结构】树与二叉树(八):二叉树的中序遍历(非递归算法NIO)
文章目录
- 5.2.1 二叉树
- 5.2.2 二叉树顺序存储
- 5.2.3 二叉树链接存储
- 5.2.4 二叉树的遍历
- 1-3 先序、中序、后序遍历递归实现及相关练习
- 中序遍历递归实现
- 4. 中序遍历非递归
- a. 算法NIO
- b. 算法解读
- c. 典例剖析
- d.代码实现
- 5. 代码整合
5.2.1 二叉树
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
二叉树性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
满二叉树、完全二叉树定义、特点及相关证明
- 详细证明过程见前文:【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.2.2 二叉树顺序存储
二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中,详见:
【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
5.2.3 二叉树链接存储
二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中,结点之间的关系用指针说明。在链式存储中,每个二叉树结点都包含三个域:数据域(Data)、左指针域(Left)和右指针域(Right),用于存储结点的信息和指向子结点的指针,详见:
【数据结构】树与二叉树(六):二叉树的链式存储
5.2.4 二叉树的遍历
- 遍历(Traversal)是对二叉树中所有节点按照一定顺序进行访问的过程。
- 通过遍历,可以访问树中的每个节点,并按照特定的顺序对它们进行处理。
- 对二叉树的一次完整遍历,可给出树中结点的一种线性排序。
- 在二叉树中,常用的遍历方式有三种:先序遍历、中序遍历和后序遍历。
- 这三种遍历方式都可以递归地进行,它们的区别在于节点的访问顺序。
- 在实现遍历算法时,需要考虑递归终止条件和递归调用的顺序。
- 还可以使用迭代的方式来实现遍历算法,使用栈或队列等数据结构来辅助实现。
- 遍历是二叉树中基础而重要的操作,它为其他许多操作提供了基础,如搜索、插入、删除等。
1-3 先序、中序、后序遍历递归实现及相关练习
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
中序遍历递归实现
void inOrderTraversal(struct Node* root) {if (root == NULL) {return;}// 递归遍历左子树inOrderTraversal(root->left);// 访问根节点printf("%c ", root->data);// 递归遍历右子树inOrderTraversal(root->right);
}
4. 中序遍历非递归
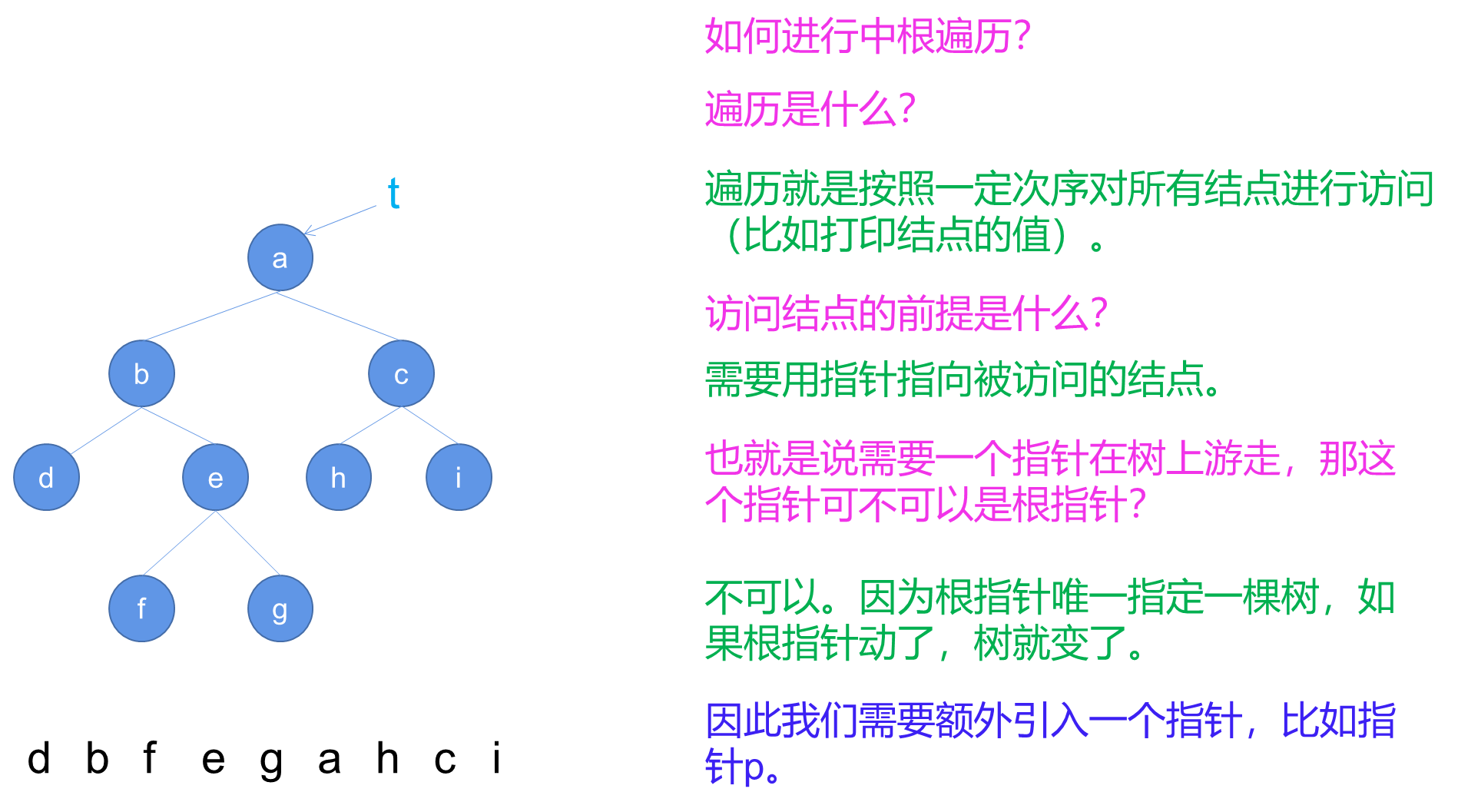
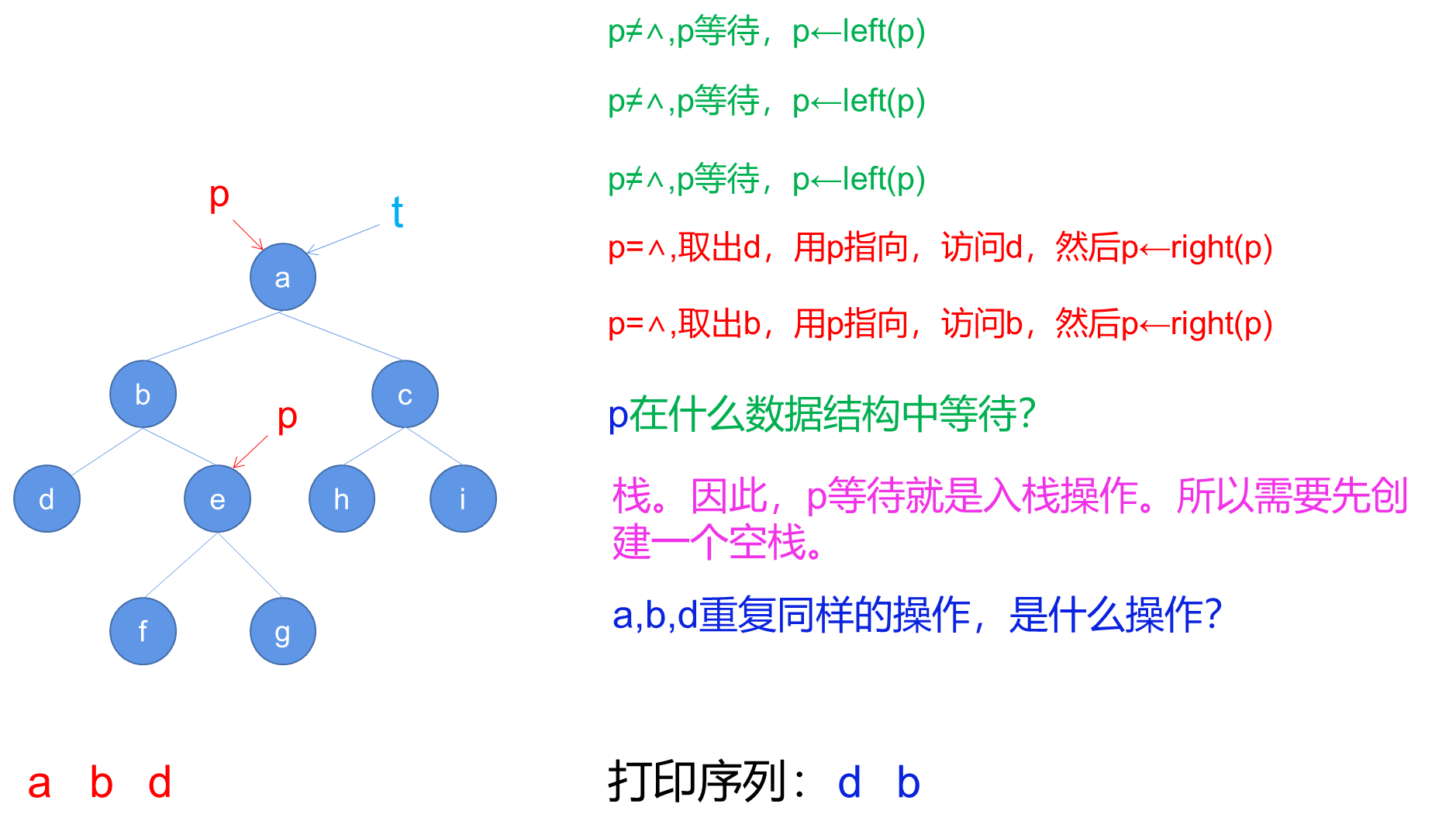
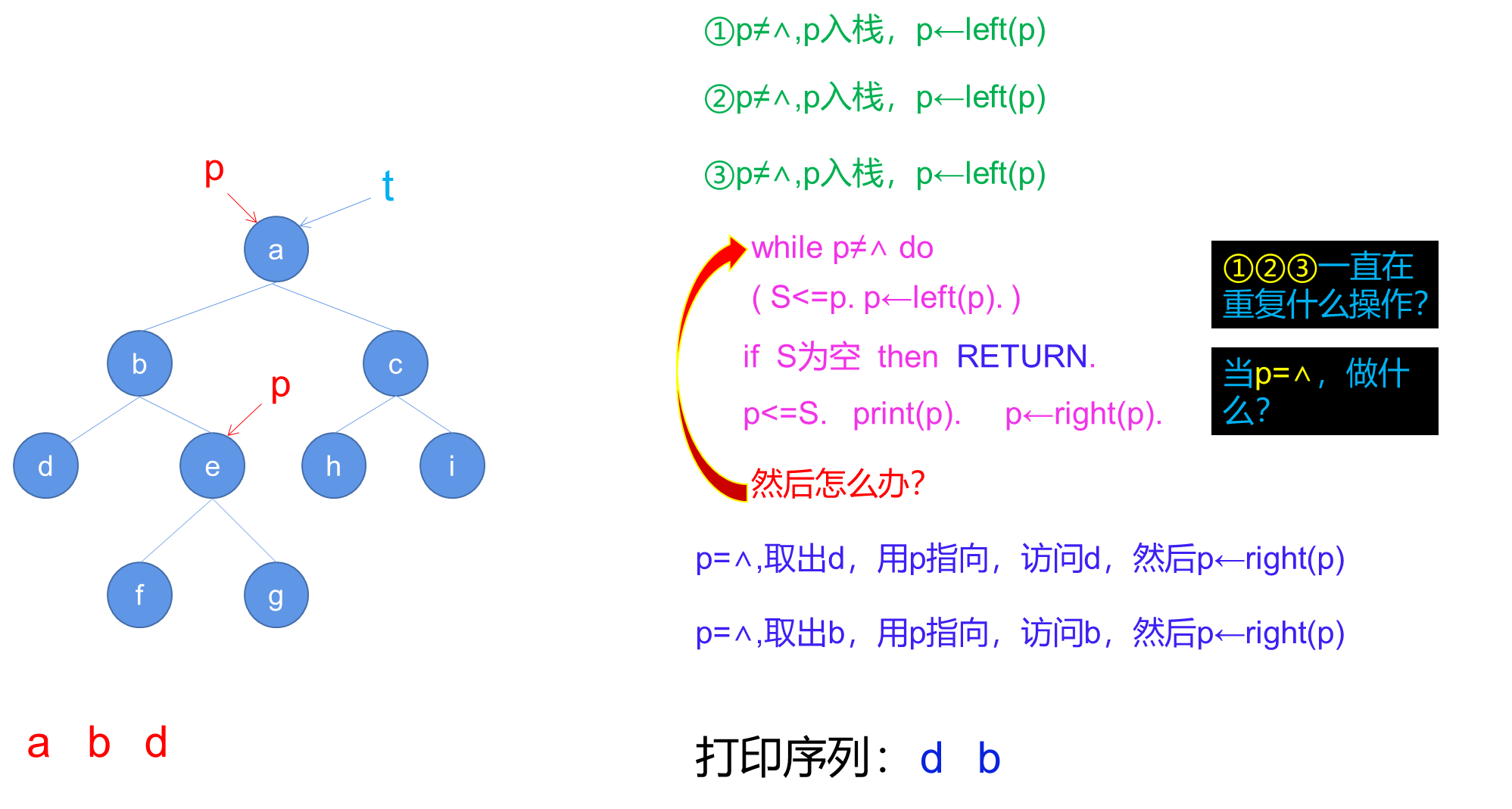
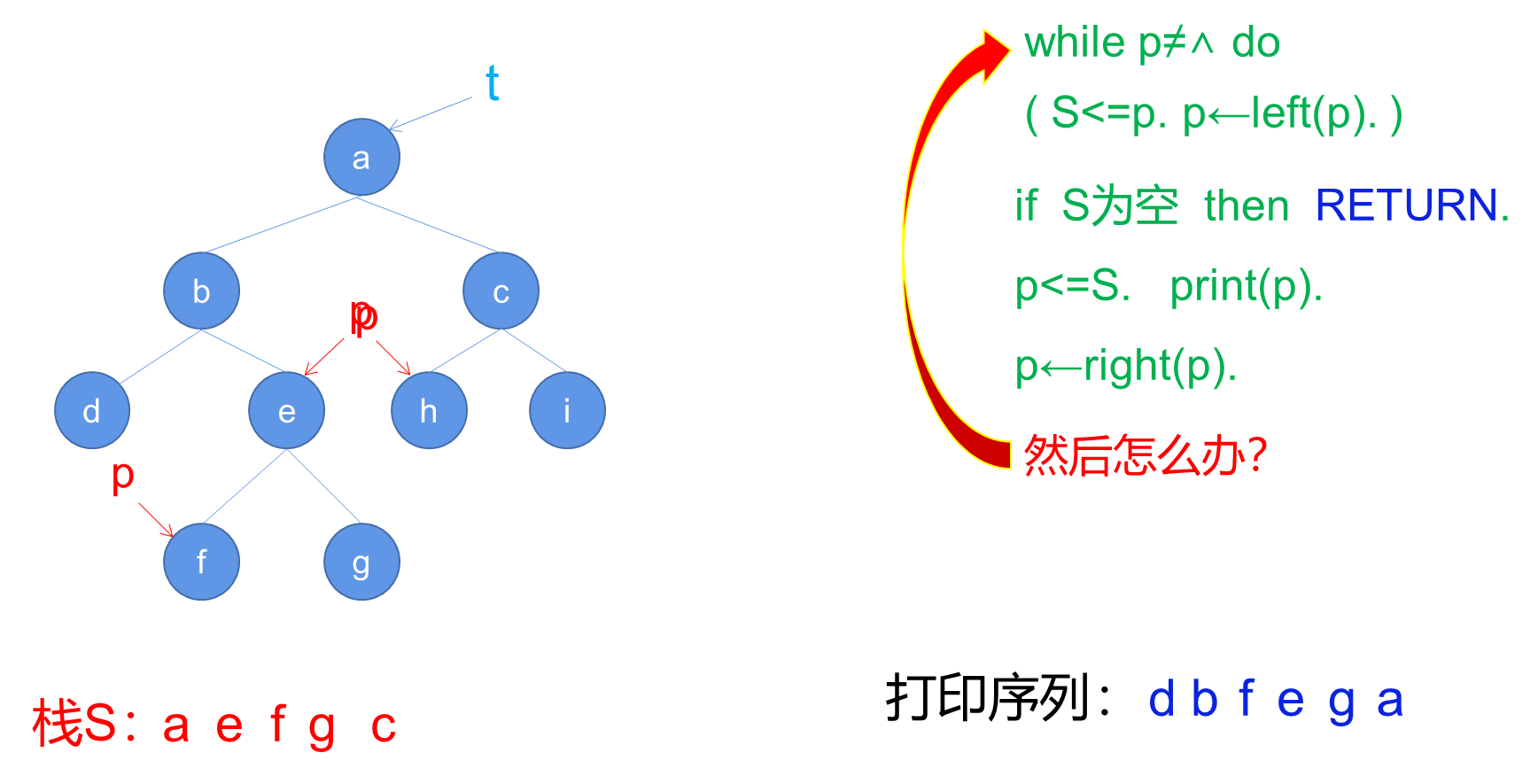
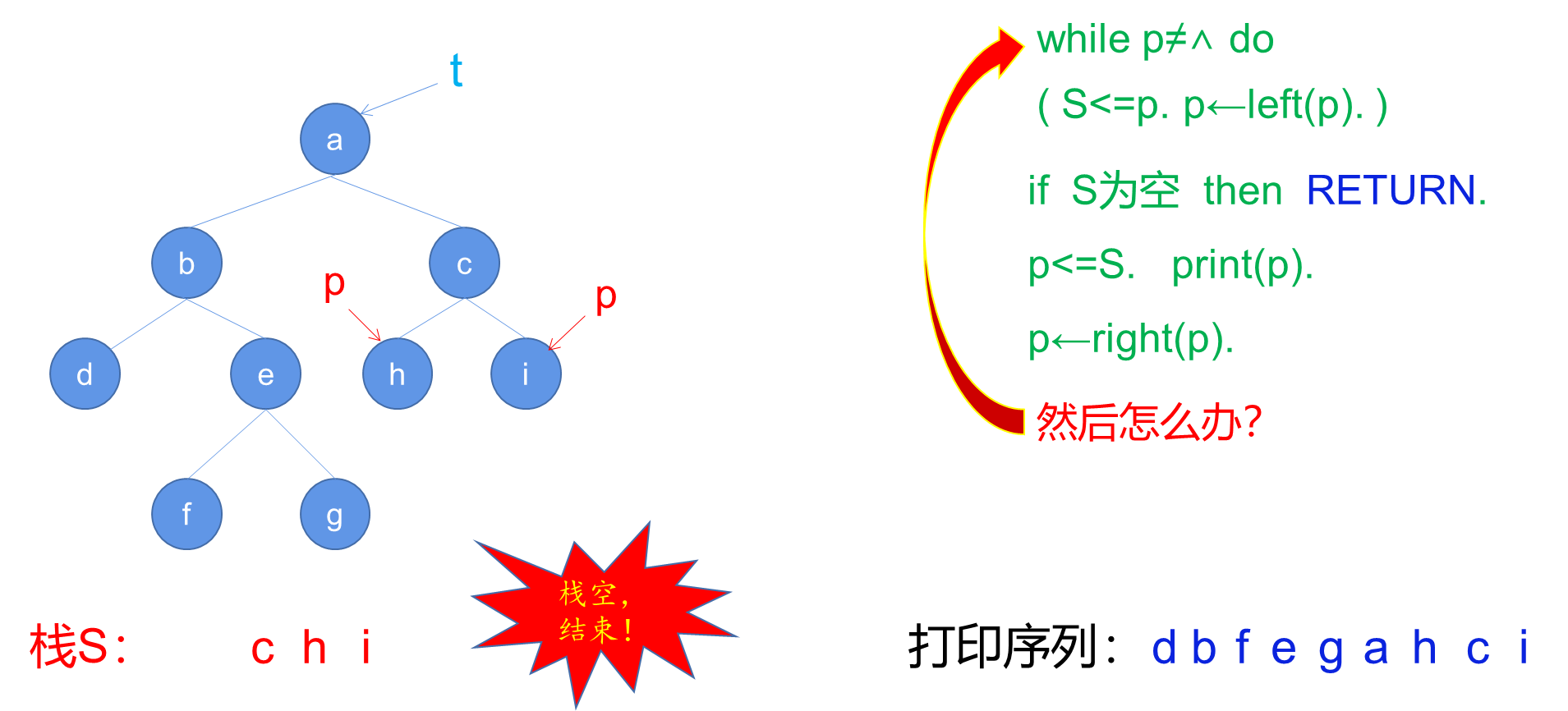
a. 算法NIO

b. 算法解读
NIO算法利用了一个辅助堆栈S来模拟递归过程中的函数调用栈。通过在循环中不断将左子节点入栈,然后处理栈顶节点,并将指针移动到右子节点,实现了中序遍历的非递归算法。
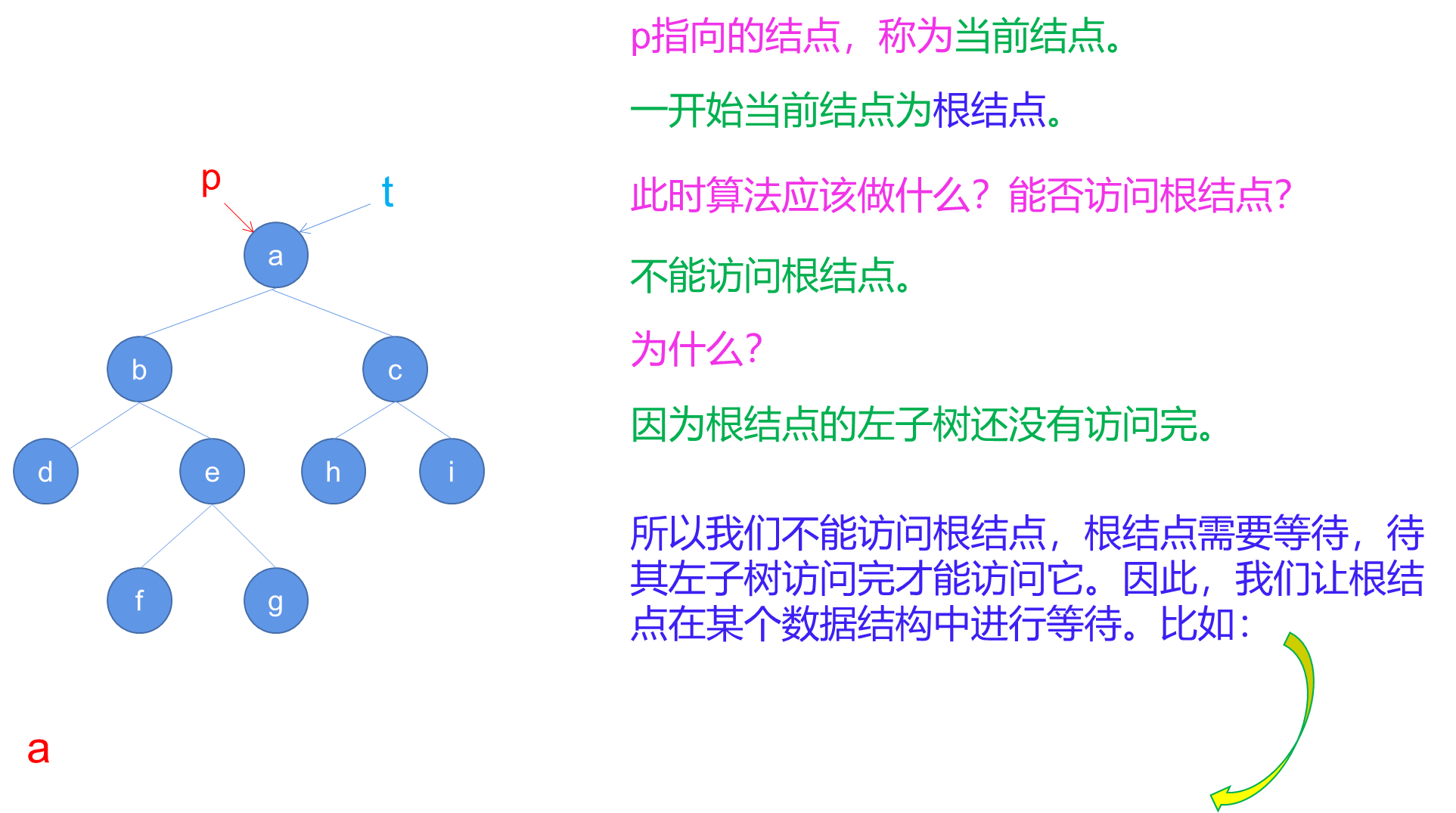
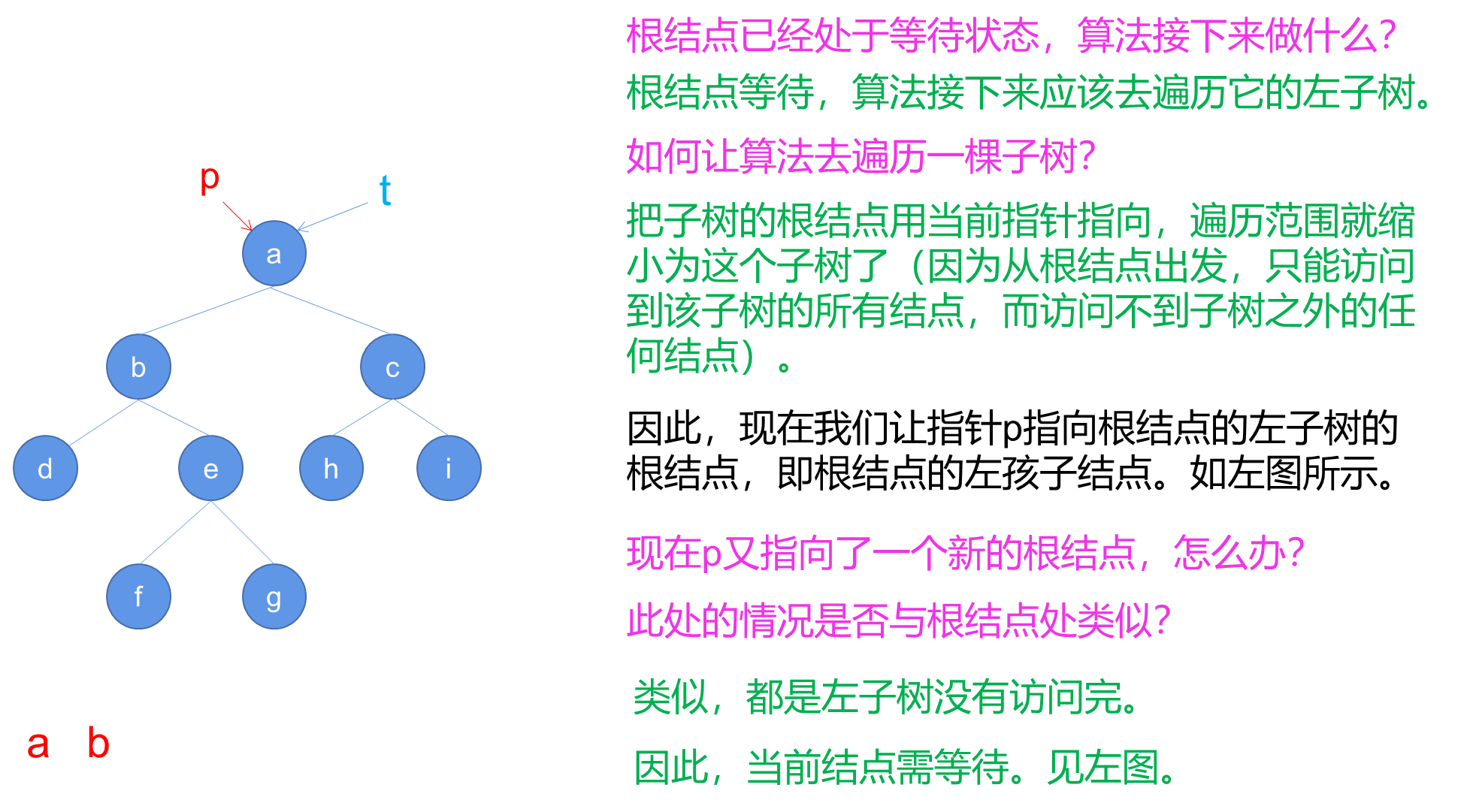
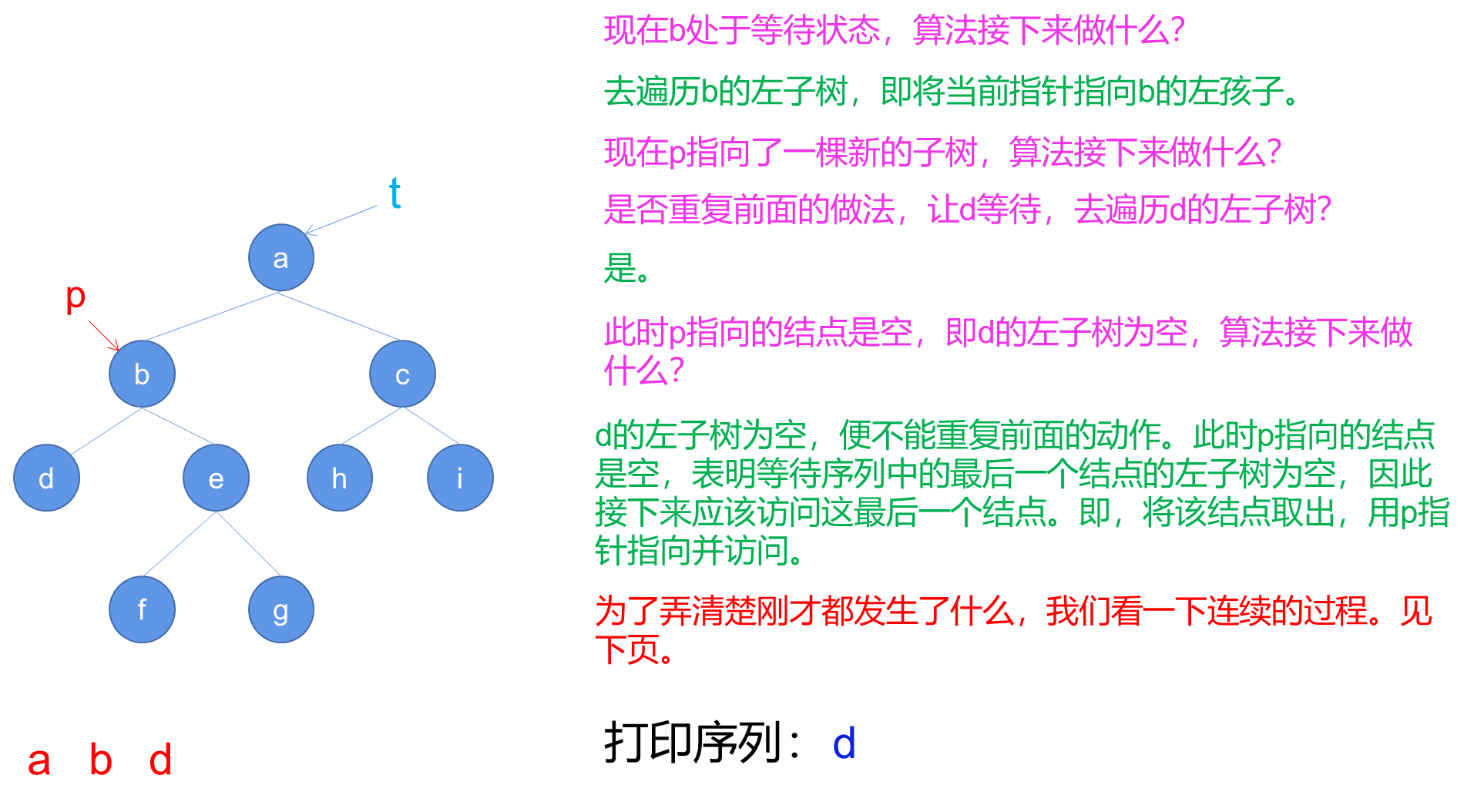
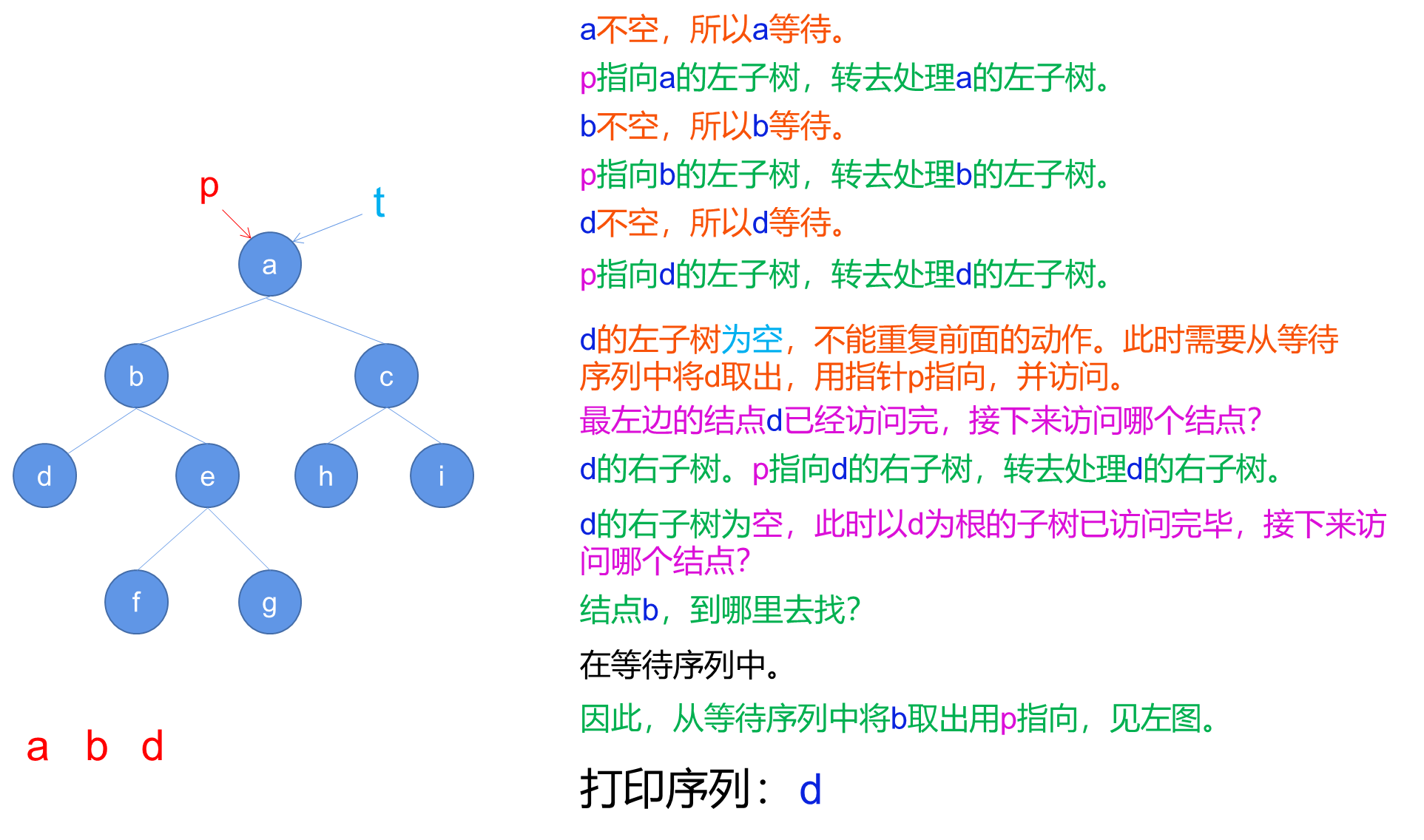
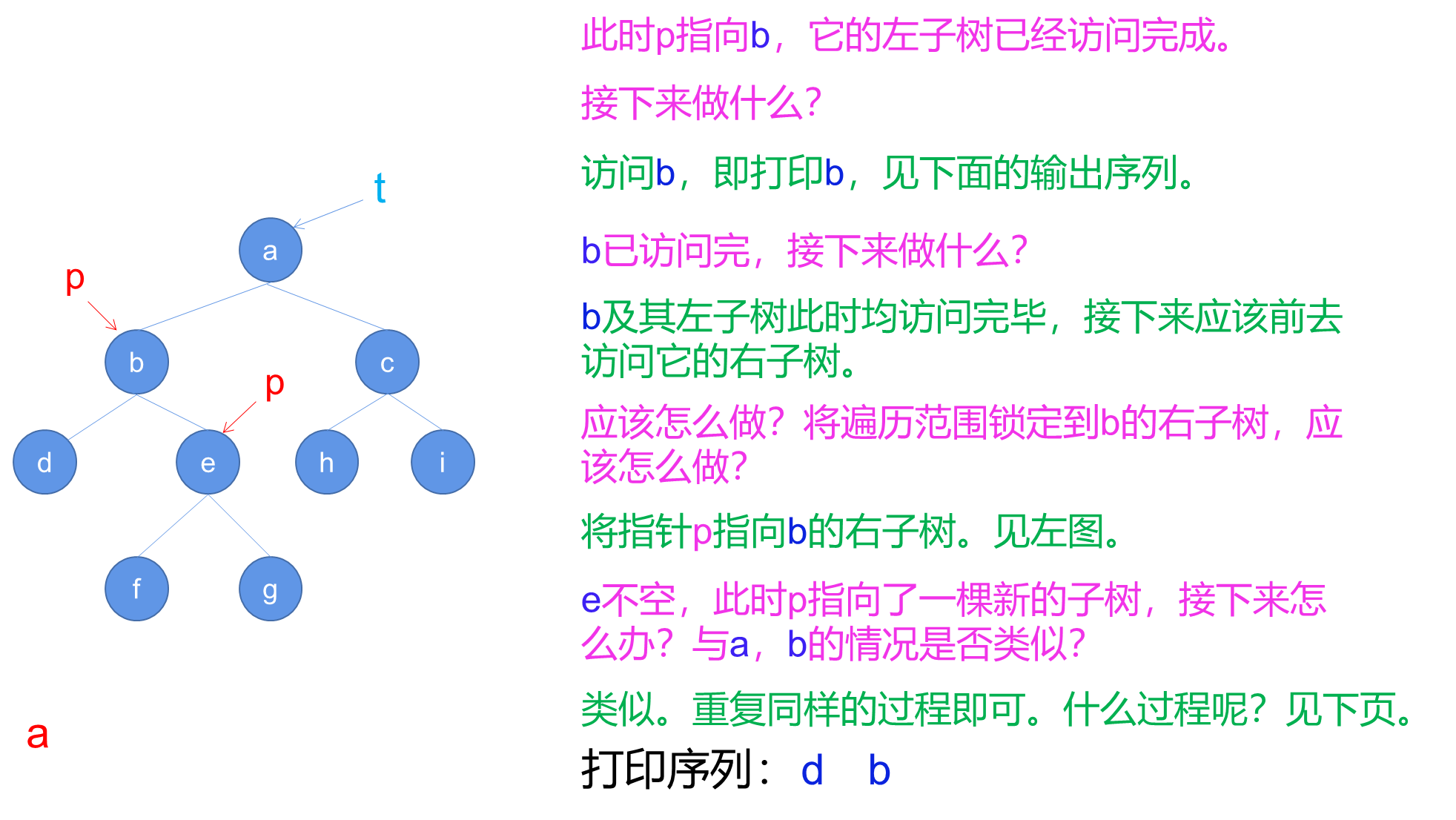
- 创建一个空堆栈S,并将指针p指向树的根节点t。
- 进入循环,只要p不为空,执行以下步骤:
a. 将p入栈S。
b. 将p指向其左子节点(p = Left( p ))。 - 如果堆栈S为空,则结束算法。
- 从堆栈S中弹出栈顶元素,并将p指向弹出的节点。
- 打印p节点的值。
- 将p指向p的右子节点(p = Right( p ))。
- 跳转到步骤2,继续循环。
该算法的时间复杂度为O(n),其中n是二叉树中节点的数量。因为每个节点都会被访问一次且入栈一次,所以算法的时间复杂度与节点数量成正比。
这个非递归中序遍历算法可以应用于需要遍历二叉树并按照中序顺序访问节点的场景,例如在构建二叉树的线索化结构时,或者需要按照中序顺序遍历二叉搜索树等情况下。
c. 典例剖析
d.代码实现
void nonRecursiveInOrder(struct Node* root) {struct Node* stack[100]; // 辅助堆栈,用于模拟递归调用栈int top = -1; // 栈顶指针struct Node* current = root;while (current != NULL || top != -1) {// 将当前结点的左子结点入栈while (current != NULL) {stack[++top] = current;current = current->left;}// 弹出栈顶结点,并访问current = stack[top--];printf("%c ", current->data);// 处理右子结点current = current->right;}
}5. 代码整合
#include <stdio.h>
#include <stdlib.h>// 二叉树结点的定义
struct Node {char data;struct Node* left;struct Node* right;
};// 创建新结点
struct Node* createNode(int data) {struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));if (newNode == NULL) {printf("Memory allocation failed!\n");exit(1);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}
// 递归中序遍历
void inOrderTraversal(struct Node* root) {if (root == NULL) {return;}// 递归遍历左子树inOrderTraversal(root->left);// 访问根节点printf("%c ", root->data);// 递归遍历右子树inOrderTraversal(root->right);
}// 非递归中序遍历
void nonRecursiveInOrder(struct Node* root) {struct Node* stack[100]; // 辅助堆栈,用于模拟递归调用栈int top = -1; // 栈顶指针struct Node* current = root;while (current != NULL || top != -1) {// 将当前结点的左子结点入栈while (current != NULL) {stack[++top] = current;current = current->left;}// 弹出栈顶结点,并访问current = stack[top--];printf("%c ", current->data);// 处理右子结点current = current->right;}
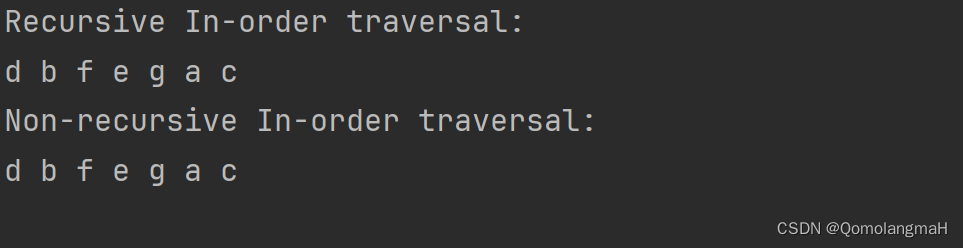
}int main() {// 创建一棵二叉树struct Node* root = createNode('a');root->left = createNode('b');root->right = createNode('c');root->left->left = createNode('d');root->left->right = createNode('e');root->left->right->left = createNode('f');root->left->right->right = createNode('g');// 递归中序遍历二叉树printf("Recursive In-order traversal: \n");inOrderTraversal(root);printf("\n");// 非递归中序遍历二叉树printf("Non-recursive In-order traversal:\n");nonRecursiveInOrder(root);printf("\n");return 0;
}
相关文章:

【数据结构】树与二叉树(八):二叉树的中序遍历(非递归算法NIO)
文章目录 5.2.1 二叉树二叉树性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉树中至多有 2 k 1 − 1 2^{k1}-1 2k1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。引理5.3&…...

第九章 排序【数据结构】【精致版】
第九章 排序【数据结构】【精致版】 前言版权第九章 排序9.1 概述9.2 插入类排序9.2.1 直接插入排序**1-直接插入排序.c** 9.2.2 折半插入排序**2-折半插入排序.c** 9.2.3 希尔排序 9.3 交换类排序9.3.1冒泡排序**4-冒泡排序.c** 9.3.2 快速排序**5-快速排序.c** 9.4 选择类排…...

基于element-plus定义表格行内编辑配置化
文章目录 前言一、新增table组件二、使用步骤 前言 在 基于element-plus定义表单配置化 基础上,封装个Element-plus的table表格 由于表格不同于form组件,需自定义校验器,以下组件配置了单个校验,及提交统一校验方法,且…...
WebGL-Vue3-TS-Threejs:基础练习 / Javascript 3D library / demo
一、理解Three.js Three.js是一个用于WebGL渲染的JavaScript库。它提供了一组工具和类,用于创建和渲染3D图形和动画。简单理解(并不十分准确),Three.js之于WebGL,好比,jQuery.js之于JavaScript。 OpenGL …...

2022年12月 Python(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
Python等级考试(1~6级)全部真题・点这里 一、单选题(共25题,每题2分,共50分) 第1题 有n个按名称排序的商品,使用对分查找法搜索任何一商品,最多查找次数为5次,则n的值可能为?()(2分) A.5 B.15 C.30 D.35 答案:C 答案解析:对分查找最多查找次数m与个数之间n的…...

确定性 vs 非确定性:GPT 时代的新编程范式
分享嘉宾 | 王咏刚 责编 | 梦依丹 出品 | 《新程序员》编辑部 在 ChatGPT 所引爆的新一轮编程革命中,自然语言取代编程语言,在只需编写提示词/拍照就能出程序的时代,未来程序员真的会被简化为提示词的编写员吗?通过提示词操纵 …...

【Linux奇遇记】我和Linux的初次相遇
🌈个人主页: Aileen_0v0 🔥系列专栏:Linux奇遇记系列专栏💫"没有罗马,那就自己创造罗马~" 目录 前端和后端的介绍 1.前端 2.后端 3.前后端区别 Linux在前后端开发中的角色 如何学习Linux 去进行程序开发 Linux的常见根目…...
剪贴板劫持--PasteJacker的使用
启动 PasteJacker [1] Windows [2] Linux [3] Exit第一次是让我们选择要攻击针对的目标系统,这里以Windows系统为例,即我自己的物理机 因此键入 1 ,回车 [1] Download and execute a msfvenom backdoor using certutil (Web delivery Past…...

说一下vue2的响应式原理?
vue2采用数据代理数据劫持发布订阅模式的方法。 在初始化vue实例时,会把data对象和data对象的属性都添加到vm对象中,通过object.defineProperty()进行数据代理,用vm对象的属性来代理data对象的属性,并在Observer类中递归遍历data…...

如何使用CORS和CSP保护前端应用程序安全
前端应用在提供无缝用户体验方面起着核心作用。在当今互联网的环境中,第三方集成和API的普及使得确保强大的安全性至关重要。安全漏洞可能导致数据盗窃、未经授权访问以及品牌声誉受损。本文将向您展示如何使用CORS和CSP为您的网页增加安全性。 嗨,大家好…...

C/C++输出硬币翻转 2021年6月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C硬币翻转 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C硬币翻转 2021年6月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 假设有N个硬币(N为不大于5000的正整数),从1…...

ipad可能会在iOS 16中失去智能家居中心功能
在iOS 16测试版代码中发现的文本表明苹果将放弃对iPad家庭中心的支持 家庭app迎来重大改版,未来更将对智能家居互联互通标准Matter提供支持。 即使某一款智能家居设备再优秀,只要它没有接入HomeKit,那么就不能在苹果的家庭app中直接管理控制。…...

maven打包可运行jar
普通java程序 <build><finalName>JavaDeviceClient</finalName><plugins><plugin><artifactId>maven-compiler-plugin</artifactId><version>2.3.2</version><configuration><source>1.8</source><…...

Arcgis连接Postgis数据库(Postgre入门十)
效果 步骤 1、矢量数据首先有在postgis数据库中 这个postgis数据库中的一个空间数据,数据库名称是test3,数据表名称是test 2、Arcgis中连接postgis数据库中 3、成功连接 可以将数据拷贝或导入到gdb数据库中...

【蓝桥杯选拔赛真题17】C++时间换算 第十二届蓝桥杯青少年创意编程大赛C++编程选拔赛真题解析
目录 C/C++时间换算 一、题目要求 1、编程实现 2、输入输出 二、算法分析 <...
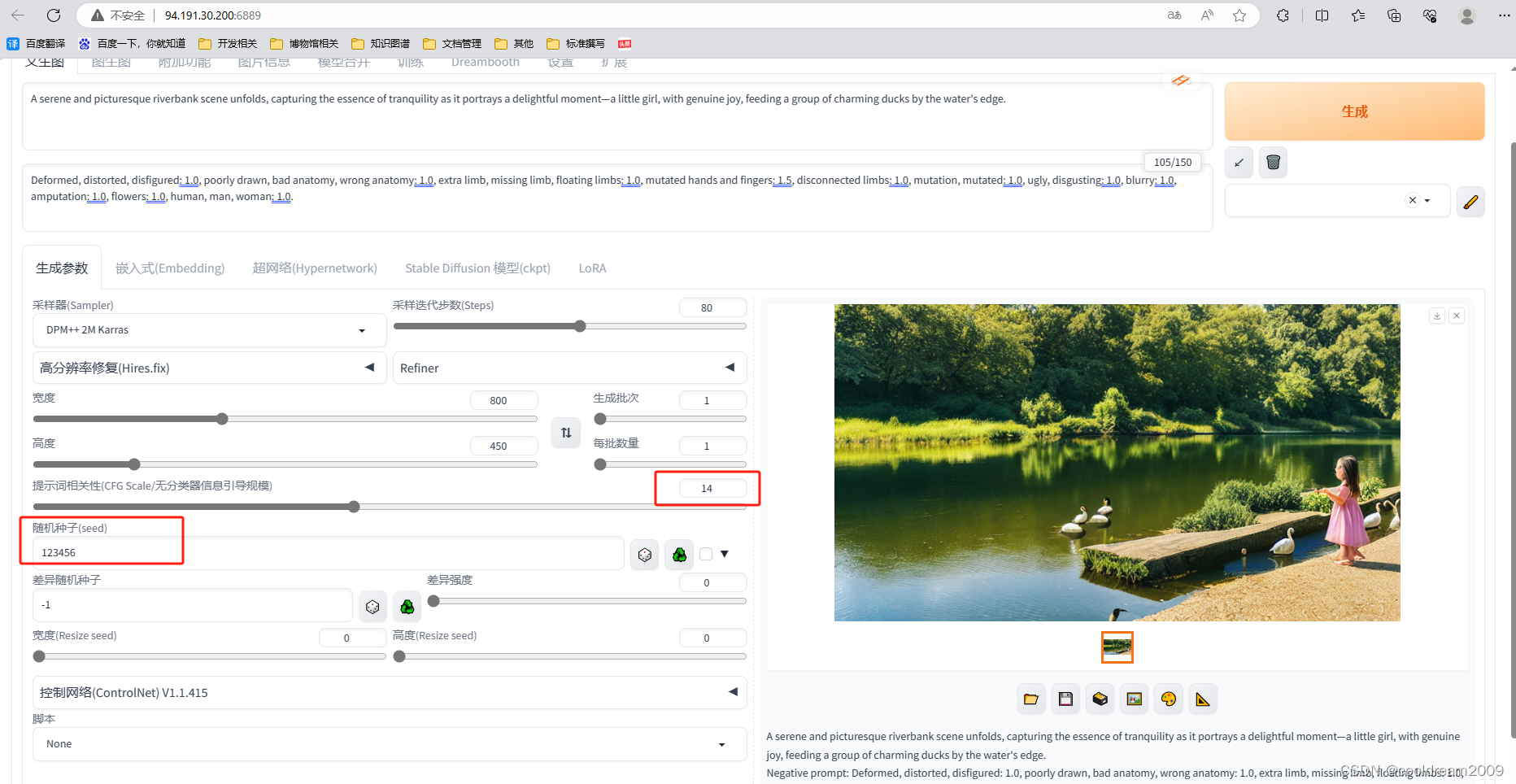
【腾讯云 HAI域探秘】探索AI绘画之路:利用腾讯云HAI服务打造智能画家
目录 前言1 使用HAI服务作画的步骤1.1 注册腾讯云账户1.2 创建算力服务器1.3 进入模型管理界面1.4 汉化界面1.5 探索AI绘画 2 模型参数的含义和调整建议2.1 模型参数的含义和示例2.2 模型参数的调整建议 3 调整参数作画的实践和效果3.1 实践说明3.2 实践效果13.3 实践效果23.4 …...
)
安卓常见设计模式10------责任链模式(Kotlin版)
1. W1 是什么,什么是责任链模式? 责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,它用于将请求的发送者和接收者解耦,并将请求沿着一个处理链进行传递,直到有一个处理者能…...

利用 Google Artifact Repository 构建maven jar 存储仓库
参考了google 官方文档 https://cloud.google.com/artifact-registry/docs/java/store-java#gcloud_1 首先 enable GAR api gcloud services enable artifactregistry.googleapis.com gcloud services list | grep -i artifact artifactregistry.googleapis.com Artifac…...
Facebook广告被暂停是什么原因?Facebook广告账号被封怎么办?
许多做海外广告投放的小伙伴经常遇到一个难题,那就是投放的Facebook广告被拒或 Facebook 广告帐户被关闭赞停的经历,随之而来的更可能是广告账户被封,导致资金的损失。本文将从我自身经验,为大家分享,Facebook广告被暂…...

Javaweb之javascript的BOM对象的详细解析
1.5.2 BOM对象 接下来我们学习BOM对象,BOM的全称是Browser Object Model,翻译过来是浏览器对象模型。也就是JavaScript将浏览器的各个组成部分封装成了对象。我们要操作浏览器的部分功能,可以通过操作BOM对象的相关属性或者函数来完成。例如:…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
