[PyTorch][chapter 61][强化学习-免模型学习 off-policy]
前言:
蒙特卡罗的学习基本流程:
Policy Evaluation : 生成动作-状态轨迹,完成价值函数的估计。
Policy Improvement: 通过价值函数估计来优化policy。
同策略(one-policy):产生 采样轨迹的策略 和要改善的策略
相同。
Policy Evaluation : 通过-贪心策略(
),产生(状态-动作-奖赏)轨迹。
Policy Improvement: 原始策略也是 -贪心策略(
), 通过价值函数优化,
-贪心策略(
)
异策略(off-policy):产生采样轨迹的 策略 和要改善的策略
不同。
Policy Evaluation : 通过-贪心策略(
),产生采样轨迹(状态-动作-奖赏)。
Policy Improvement: 改进原始策略
两个优势:
1: 原始策略不容易采样
2: 降低方差
易策略常用的方案为 IR(importance sample) 重要性采样
Importance sampling is a Monte Carlo method for evaluating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest. Its introduction in statistics is generally attributed to a paper by Teun Kloek and Herman K. van Dijk in 1978,[1] but its precursors can be found in statistical physics as early as 1949.[2][3] Importance sampling is also related to umbrella sampling in computational physics. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both.
一 importance-samling

1.1 原理
原始问题:
如果采样N次,得到
问题: 很难采样(采样空间很大,很多时候只能采样到一部分)
引入 q(x) 重要性分布(这也是一个分布,容易被采样)
: 称为importance weight
(大数定理)
下面例子,我们需要对,做归一化处理,更清楚的看出来占比
下面代码进行了归一化处理,方案如下:
# -*- coding: utf-8 -*-
"""
Created on Wed Nov 8 16:38:34 2023@author: chengxf2
"""import numpy as np
import matplotlib.pyplot as plt
from scipy.special import logsumexpclass pdf:def __call__(self,x):passdef sample(self,n):pass#正太分布的概率密度
class Norm(pdf):#返回一组符合高斯分布的概率密度随机数。def __init__(self, mu=0, sigma=1):self.mu = muself.sigma = sigmadef __call__(self, x):#log p 功能,去掉前面常数项logp = (x-self.mu)**2/(2*self.sigma**2)return -logpdef sample(self, N):#产生N 个点,这些点符合正太分布x = np.random.normal(self.mu, self.sigma,N)return xclass Uniform(pdf):#均匀分布的概率密度def __init__(self, low, high):self.low = lowself.high = highdef __call__(self, x):#logq 功能N = len(x)a = np.repeat(-np.log(self.high-self.low), N)return -adef sample(self, N):#产生N 点,这些点符合均匀分布x = np.random.uniform(self.low, self.high,N)return xclass ImportanceSampler:def __init__(self, p_dist, q_dist):self.p_dist = p_distself.q_dist = q_distdef sample(self, N):#采样samples = self.q_dist.sample(N)weights = self.calc_weights(samples)normal_weights = weights - logsumexp(weights)return samples, normal_weightsdef calc_weights(self, samples):#log (p/q) =log(p)-log(q)return self.p_dist(samples)-self.q_dist(samples)if __name__ == "__main__":N = 10000p = Norm()q = Uniform(-10, 10) sampler = ImportanceSampler(p, q)#samples 从q(x)采样出来的点,weight_samplesamples,weight_sample= sampler.sample(N)#以weight_sample的概率,从samples中抽样 N 个点samples = np.random.choice(samples,N, p = np.exp(weight_sample))plt.hist(samples, bins=100)二 易策略 off-policy 原理

target policy : 原始策略
: 这里面代表基于原始策略,得到的轨迹
该轨迹的概率
: 该轨迹的累积奖赏
期望的累积奖赏:
behavior policy : 行为策略
q(x): 代表各种轨迹的采样概率
则累积奖赏函数f在概率p 也可以等价的写为:
和
分别表示两个策略产生i 条轨迹的概率,对于给定的一条轨迹
:
原始策略 产生该轨迹的概率:
则
若 为确定性策略,但是
是
的
贪心策略:
原始策略
行为策略:
现在通过行为策略产生的轨迹度量权重w
理论上应该是连乘的,但是,
考虑到只是概率的比值,上面可以做个替换
其中: (更灵活的利用importance sample)
其核心是要计算两个概率比值,上面的例子是去log,再归一化
三 方差影响

四 代码

代码里面R的计算方式跟上面是不同的,
# -*- coding: utf-8 -*-
"""
Created on Wed Nov 8 11:56:26 2023@author: chengxf2
"""import numpy as ap
# -*- coding: utf-8 -*-
"""
Created on Fri Nov 3 09:37:32 2023@author: chengxf2
"""# -*- coding: utf-8 -*-
"""
Created on Thu Nov 2 19:38:39 2023@author: cxf
"""
import numpy as np
import random
from enum import Enumclass State(Enum):#状态空间#shortWater =1 #缺水health = 2 #健康overflow = 3 #溢水apoptosis = 4 #凋亡class Action(Enum):#动作空间A#water = 1 #浇水noWater = 2 #不浇水class Env():def reward(self, state):#针对转移到新的环境奖赏 r = -100if state is State.shortWater:r =-1elif state is State.health:r = 1elif state is State.overflow:r= -1else: # State.apoptosisr = -100return rdef action(self, state, action):if state is State.shortWater:if action is Action.water :newState =[State.shortWater, State.health]p =[0.4, 0.6]else:newState =[State.shortWater, State.apoptosis]p =[0.4, 0.6]elif state is State.health:#健康if action is Action.water :newState =[State.health, State.overflow]p =[0.6, 0.4]else:newState =[State.shortWater, State.health]p =[0.6, 0.4]elif state is State.overflow:#溢水if action is Action.water :newState =[State.overflow, State.apoptosis]p =[0.6, 0.4]else:newState =[State.health, State.overflow]p =[0.6, 0.4]else: #凋亡newState=[State.apoptosis]p =[1.0]#print("\n S",S, "\t prob ",proba)nextState = random.choices(newState, p)[0]r = self.reward(nextState)return nextState,rdef __init__(self):self.name = "环境空间"class Agent():def initPolicy(self):#初始化累积奖赏self.Q ={} #(state,action) 的累积奖赏self.count ={} #(state,action) 执行的次数for state in self.S:for action in self.A:self. Q[state, action] = 0.0self.count[state,action]= 0action = self.randomAction()self.policy[state]= Action.noWater #初始化都不浇水def randomAction(self):#随机策略action = random.choices(self.A, [0.5,0.5])[0]return actiondef behaviorPolicy(self):#使用e-贪心策略state = State.shortWater #从缺水开始env = Env()trajectory ={}#[s0,a0,r0]--[s1,a1,r1]--[sT-1,aT-1,rT-1]for t in range(self.T):#选择策略rnd = np.random.rand() #生成随机数if rnd <self.epsilon:action =self.randomAction()else:#通过原始策略选择actionaction = self.policy[state] newState,reward = env.action(state, action) trajectory[t]=[state,action,reward]state = newStatereturn trajectorydef calcW(self,trajectory):#计算权重q1 = 1.0-self.epsilon+self.epsilon/2.0 # a== 原始策略q2 = self.epsilon/2.0 # a!=原始策略w ={}for t, value in trajectory.items():#[state, action,reward]action =value[1]state = value[0]if action == self.policy[state]:p = 1q = q1else:p = 0q = q2w[t] = round(np.exp(p-q),3)#print("\n w ",w)return wdef getReward(self,t,wDict,trajectory):p = 1.0r= 0#=[state,action,reward]for i in range(t,self.T):r+=trajectory[t][-1]w =wDict[t]p =p*wR = p*rm = self.T-treturn R/mdef improve(self):a = Action.noWaterfor state in self.S:maxR = self.Q[state, a]for action in self.A:R = self.Q[state,action]if R>=maxR:maxR = Rself.policy[state]= actiondef learn(self):self.initPolicy()for s in range(1,self.maxIter): #采样第S 条轨迹#通过行为策略(e-贪心策略)产生轨迹trajectory =self.behaviorPolicy()w = self.calcW(trajectory)print("\n 迭代次数 %d"%s ,"\t 缺水:",self.policy[State.shortWater].name,"\t 健康:",self.policy[State.health].name,"\t 溢水:",self.policy[State.overflow].name,"\t 凋亡:",self.policy[State.apoptosis].name)#策略评估for t in range(self.T):R = self.getReward(t, w,trajectory)state = trajectory[t][0]action = trajectory[t][1]Q = self.Q[state,action]count = self.count[state, action]self.Q[state,action] = (Q*count+R)/(count+1)self.count[state, action]=count+1#获取权重系数self.improve() def __init__(self):self.S = [State.shortWater, State.health, State.overflow, State.apoptosis]self.A = [Action.water, Action.noWater]self.Q ={} #累积奖赏self.count ={}self.policy ={} #target Policyself.maxIter =500self.epsilon = 0.2self.T = 10if __name__ == "__main__":agent = Agent()agent.learn()https://img2020.cnblogs.com/blog/1027447/202110/1027447-20211013112906490-1926128536.png
相关文章:
[PyTorch][chapter 61][强化学习-免模型学习 off-policy]
前言: 蒙特卡罗的学习基本流程: Policy Evaluation : 生成动作-状态轨迹,完成价值函数的估计。 Policy Improvement: 通过价值函数估计来优化policy。 同策略(one-policy):产生 采样轨迹的策略 和要改…...

【服务器学习】 iomanager IO协程调度模块
iomanager IO协程调度模块 以下是从sylar服务器中学的,对其的复习; 参考资料 继承自协程调度器,封装了epoll,支持为socket fd注册读写事件回调函数 IO协程调度还解决了调度器在idle状态下忙等待导致CPU占用率高的问题。IO协程调…...

前端设计模式之【迭代器模式】
文章目录 前言介绍实现接口优缺点应用场景后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端设计模式 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误&a…...

Linux-用户与用户组,权限
1.用户组管理(以下命令需root用户执行) ①创建用户组 groupadd 用户组名 ②删除用户组 groupdel 用户组名 2.用户管理(以下命令需root用户执行) ①创建用户 useradd [-g -d] 用户名 >-g:指定用户的组,不…...

使用nvm-windows在Windows下轻松管理多个Node.js版本
Node.js是一个非常流行的JavaScript运行时环境,许多开发者在开发过程中可能需要在不同的Node.js版本之间进行切换。在Windows操作系统下,我们可以使用nvm-windows来轻松管理多个Node.js版本。本文将详细介绍如何安装和使用nvm-windows。 什么是nvm-wind…...

2023.11.10 hadoop,hive框架概念,基础组件
目录 分布式和集群的概念: hadoop架构的三大组件:Hdfs,MapReduce,Yarn 1.hdfs 分布式文件存储系统 Hadoop Distributed File System 2.MapReduce 分布式计算框架 3.Yarn 资源调度管理框架 三个组件的依赖关系是: hive数据仓库处理工具 hive的大体流程: Apache hive的…...
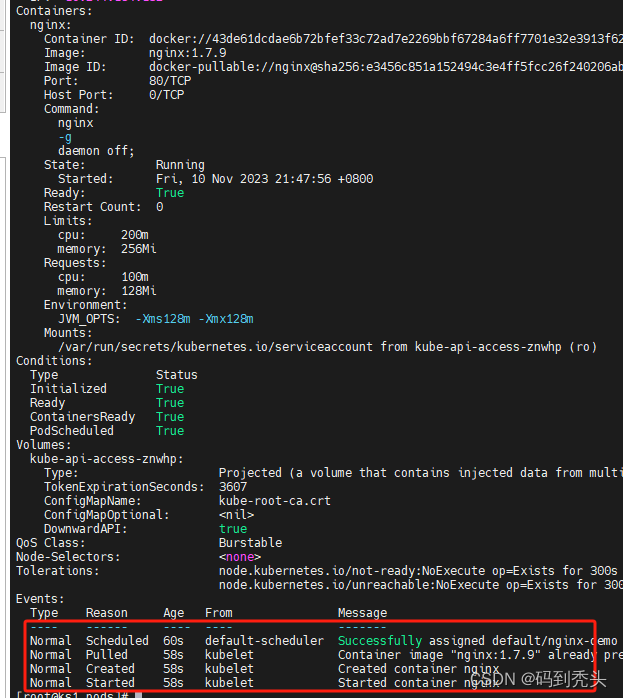
Kubernetes 创建pod的yaml文件-简单版-nginx
apiVersion: v1 #api文档版本 kind: Pod # 资源类型 Deployment,StatefulSet之类 metadata: #pod元数据 描述信息 name: nginx-demo labels: type: app #自定义标签 version: 1.0.0 # 自定义pod版本 namespace: default spec: #期望Pod按照这里的描述创建 cont…...
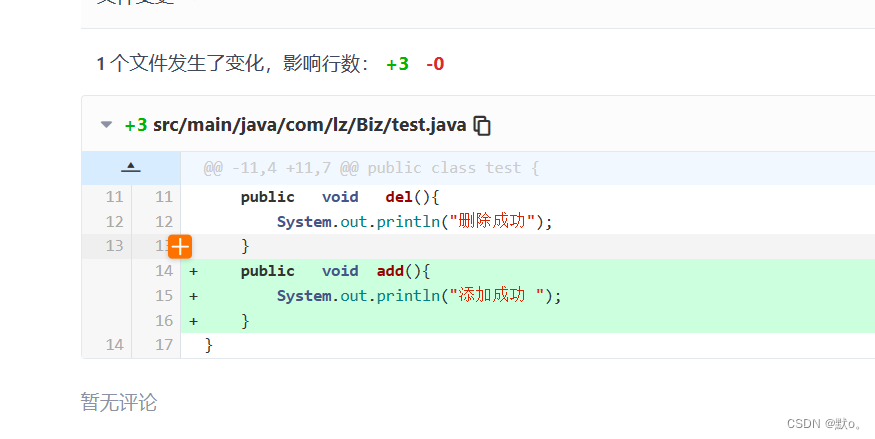
Git的进阶操作,在idea中部署gie
🏅我是默,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《git》。🎯🎯 🚀无论你是编程小白,还是有一定基础的程序员,这…...
)
设计模式-迭代器模式(Iterator)
设计模式-迭代器模式(Iterator) 一、迭代器模式概述1.1 什么是迭代器模式1.2 简单实现迭代器模式1.3 使用迭代器模式的注意事项 二、迭代器模式的用途三、迭代器模式实现方式3.1 使用Iterator接口实现迭代器模式3.2 使用Iterable接口和Iterator接口实现迭…...
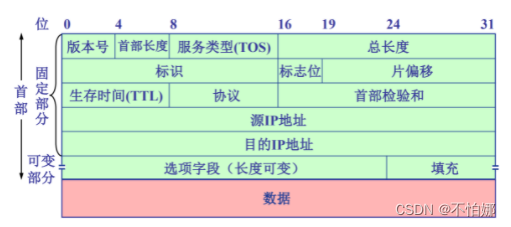
【计算机网络笔记】Internet网络的网络层——IP协议之IP数据报的结构
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...
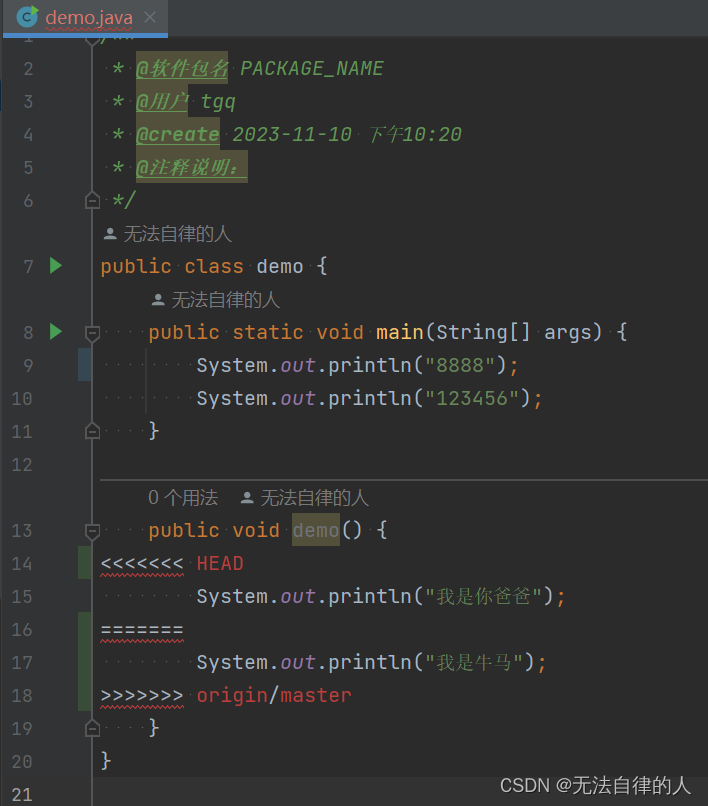
【Git】Git的GUI图形化工具ssh协议IDEA集成Git
一、GIT的GUI图形化工具 1、介绍 Git自带的GUI工具,主界面中各个按钮的意思基本与界面文字一致,与git的命令差别不大。在了解自己所做的操作情况下,各个功能点开看下就知道是怎么操作的。即使不了解,只要不做push操作,…...

Java中抽象类
1 抽象方法必须包含在抽象类中 package charactor; public abstract class Hero { String name; float hp;float armor;int moveSpeed;public static void main(String[] args) {}// 抽象方法attack // Hero的子类会被要求实现attack方法 public abstract void attack();} …...

18 Linux 阻塞和非阻塞 IO
一、阻塞和非阻塞 IO 1. 阻塞和非阻塞简介 这里的 IO 指 Input/Output(输入/输出),是应用程序对驱动设备的输入/输出操作。当应用程序对设备驱动进行操作的时候,如果不能获取到设备资源,那么阻塞式 IO 就会将对应应用…...

多因素验证如何让企业邮箱系统登录更安全?
企业邮箱系统作为基础的办公软件之一,既是企业内外沟通的重要工具,也是连接企业多个办公平台的桥梁,往往涉及到客户隐私、业务信息、企业机密等等。为了保护邮箱账户的安全,设置登陆密码无疑是保护账户安全的常用措施之一。然而随…...

投票助手图文音视频礼物打赏流量主小程序开源版开发
投票助手图文音视频礼物打赏流量主小程序开源版开发 图文投票:用户可以发布图文投票,选择相应的选项进行投票。 音视频投票:用户可以发布音视频投票,观看音视频后选择相应的选项进行投票。 礼物打赏:用户可以在投票过…...

黑客(网络安全)技术——高效自学1.0
前言 前几天发布了一篇 网络安全(黑客)自学 没想到收到了许多人的私信想要学习网安黑客技术!却不知道从哪里开始学起!怎么学 今天给大家分享一下,很多人上来就说想学习黑客,但是连方向都没搞清楚就开始学习…...
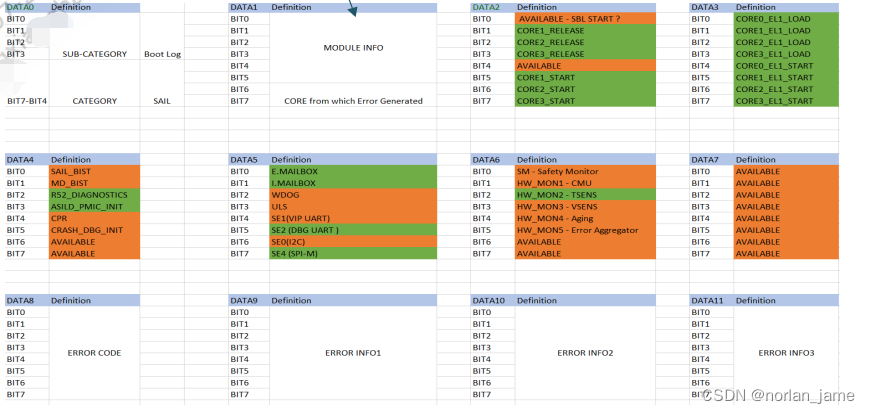
8255 boot介绍及bring up经验分享
这篇文章会简单的介绍8255的启动流程,然后着重介绍8255在实际项目中新硬件上的bring up工作,可以给大家做些参考。 8255 boot介绍 下面这些信息来自文档:《QAM8255P IVI Boot and CoreBSP Architecture Technical Overview》 80-42847-11 R…...
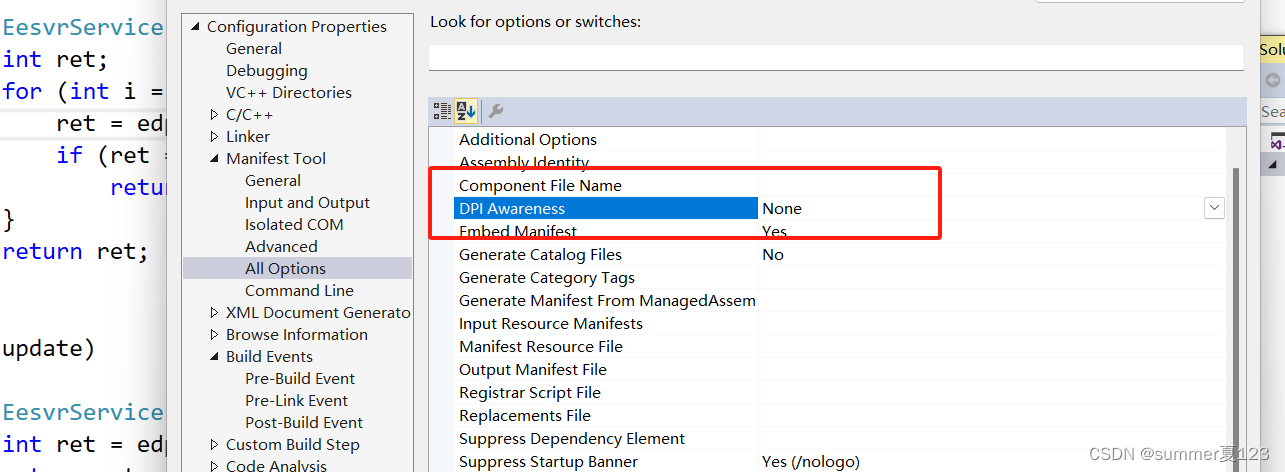
visual studio 启用DPI识别功能
在开发widow程序时,有时必须将电脑 设置-->显示-->缩放与布局-->更改文本、应用项目的大小-->100%后,程序的画面才能正确运行,居说这是锁定了dpi的原因,需要启dpi识别功能。设置方法如下: 或者...

一题三解(暴力、二分查找算法、单指针):鸡蛋掉落
涉及知识点 暴力、二分查找算法、单指针 题目 给你 k 枚相同的鸡蛋,并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。 已知存在楼层 f ,满足 0 < f < n ,任何从 高于 f 的楼层落下的鸡蛋都会碎,从 f 楼层或比它低的…...
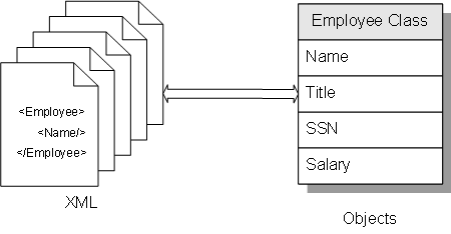
第一章 Object-XML 映射简介
文章目录 第一章 Object-XML 映射简介基础如何工作的映射选项IRIS 中的相关工具XML 文档的可能应用 第一章 Object-XML 映射简介 基础 将对象映射到 XML 一词意味着定义如何将该对象用作 XML 文档。要将对象映射到 XML,请将 %XML.Adaptor 添加到定义该对象的类的超…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
