一题三解(暴力、二分查找算法、单指针):鸡蛋掉落
涉及知识点
暴力、二分查找算法、单指针
题目
给你 k 枚相同的鸡蛋,并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。
已知存在楼层 f ,满足 0 <= f <= n ,任何从 高于 f 的楼层落下的鸡蛋都会碎,从 f 楼层或比它低的楼层落下的鸡蛋都不会破。
每次操作,你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下(满足 1 <= x <= n)。如果鸡蛋碎了,你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎,则可以在之后的操作中 重复使用 这枚鸡蛋。
请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少?
示例 1:
输入:k = 1, n = 2
输出:2
解释:
鸡蛋从 1 楼掉落。如果它碎了,肯定能得出 f = 0 。
否则,鸡蛋从 2 楼掉落。如果它碎了,肯定能得出 f = 1 。
如果它没碎,那么肯定能得出 f = 2 。
因此,在最坏的情况下我们需要移动 2 次以确定 f 是多少。
示例 2:
输入:k = 2, n = 6
输出:3
示例 3:
输入:k = 3, n = 14
输出:4
提示:
1 <= k <= 100
1 <= n <= 104
暴力解法
分析
f 取[0,n]共n+1可能 pre[i]表示i种可能 (j-1)个鸡蛋需要多少回合排除
dp[i]表示i种可能,j个鸡蛋 需要多少回合排除
只有一个鸡蛋,则测试最低的的楼层,如果破了,就得到答案;没破,就排除一种可能。当只一种可能时,不需要尝试,故:j为0时,dp[i]=i-1;
假设有j(j>2)个鸡蛋,假设在某层楼扔下,如果没破,有x种可能;破了,有i-x种可能。
则dp[i] = 1 + max(dp[x],pre[x-1]),x取值[1,i-1]
笨办法枚举x。
时间复杂度
时间复杂度O(knn),超时。
代码
class Solution {
public:
int superEggDrop(int k, int n) {
vector pre(n + 2);//f 取[0,n)共n+1可能 pre[i]表示i种可能 j个鸡蛋需要多少回合排除
for (int i = 0; i <= n+1; i++)
{
pre[i] = i - 1;
}
for (int j = 1; j < k; j++)
{
vector dp(n + 2,1000*100);
dp[1] = 0;
for (int i = 2; i <= n+1; i++)
{
for (int x = 1; x < i; x++)
{
dp[i] = min(dp[i], 1 + max(dp[x], pre[i - x]));
}
}
pre.swap(dp);
}
return pre.back();
}
};
二分
分析
重点考虑:max(dp[x], pre[i - x]));
情况一:dp[x] <= pre[i-x]
x1和x2是合法x,且x1<x2如,则x1被淘汰
证明:因为pre和dp都是单调增加或不变 。 x1<x2 > i-x1 > i-x2 =>pre[i-x1]>=pre[i-x2]
情况二:dp[x] > pre[i-x]
同理:只需要考虑最小的x
情况一最大的x是xLeft,情况二最小的x是xRight,则xRightxLeft+1
故只需求xRight,注意:xRight可能不存在
情况二符合条件,多个符合条件返回第一个,用左开右闭空间二分。
时间复杂度
O(nklogn)。枚举鸡蛋数时间复杂度O(k),枚举可能数时间复杂度O(n),计算xRight时间复杂度O(logn)。
代码
class Solution {
public:int superEggDrop(int k, int n) {vector<int> pre(n + 2);//f 取[0,n)共n+1可能 pre[i]表示i种可能 j个鸡蛋需要多少回合排除for (int i = 0; i <= n + 1; i++){pre[i] = i - 1;}for (int j = 1; j < k; j++){vector<int> dp(n + 2, 1000 * 100);dp[0] = dp[1] = 0;for (int i = 2; i <= n + 1; i++){int left = 0, right = i ;while (right - left > 1){const auto mid = left + (right - left) / 2;if (dp[mid] > pre[i - mid]){right = mid;}else{left = mid;}}if (right < i ){auto x = right;dp[i] = min(dp[i], 1 + max(dp[x], pre[i - x]));}if (right >= 2){auto x = right-1;dp[i] = min(dp[i], 1 + max(dp[x], pre[i - x]));}}pre.swap(dp);}return pre.back();}
};
单指针
随着i的增加,xRight只会增加或变大。每个j,xRight的时间复杂度是O(n),总时间复杂度是O(kn)。
测试用例
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i], v2[i]);
}
}
int main()
{
int res = 0;
{
res = Solution().superEggDrop(2, 6);
Assert(3, res);
}
{
res = Solution().superEggDrop(3, 14);
Assert(4, res);
}
{
res = Solution().superEggDrop(10, 100);
Assert(7, res);
}
{
res = Solution().superEggDrop(9, 89);
Assert(7, res);
}
{
res = Solution().superEggDrop(100, 10000);
Assert(14, res);
}
//CConsole::Out(res);
}
2023年1月7号版
class Solution {
public:
int superEggDrop(int k, int n) {
int iMaxStep = MaxStep(k,n);
vector preDp(iMaxStep + 1);
int iMinSetp = INT_MAX;
for (int i = 0; i <= iMaxStep; i++)
{
preDp[i] = i+1;
if (i + 1 -1 >= n)
{
iMinSetp = i;
}
}
while (–k)
{
vector dp(iMaxStep + 1);
dp[0] = 1;
for (int i = 1; i <= iMaxStep; i++)
{
const int tmp = dp[i - 1] + preDp[i - 1];
dp[i] = tmp;
if (tmp > n)
{
iMinSetp = i;
break;
}
}
preDp.swap(dp);
}
return iMinSetp;
}
int MaxStep(int k, int n)const
{
int iOpeNum = 0;
int iCan = 1;//iOpeNum回合可以判定胡楼层
for (int i = 2; i < 10000; i++)
{
for (int j = 0; j < k; j++)
{
if (iCan > n)
{
return iOpeNum;
}
iCan /= (i - 1);
iCan *= i;
iOpeNum++;
}
}
return 100;
}
};
2023年1月8号版
枚举各回合,能判断多少种可能。
class Solution{
public:
int superEggDrop(int k, int n) {
//dp[j] 表示iStep回合,j个鸡蛋能表示的可能
vector pre(k + 1,2);
pre[0] = 1;
if (2 > n)
{
return 1;
}
for (int iStep = 2; iStep < 20000; iStep++)
{
vector dp(k + 1, 1);
for (int j = 1; j <= k; j++)
{
dp[j] = pre[j] + pre[j - 1];
if (dp[j] > n)
{
return iStep;
}
}
pre.swap(dp);
}
return -1;
}
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 洒家想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

一题三解(暴力、二分查找算法、单指针):鸡蛋掉落
涉及知识点 暴力、二分查找算法、单指针 题目 给你 k 枚相同的鸡蛋,并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。 已知存在楼层 f ,满足 0 < f < n ,任何从 高于 f 的楼层落下的鸡蛋都会碎,从 f 楼层或比它低的…...
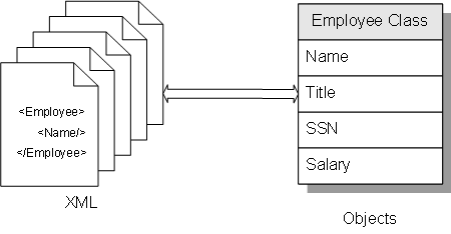
第一章 Object-XML 映射简介
文章目录 第一章 Object-XML 映射简介基础如何工作的映射选项IRIS 中的相关工具XML 文档的可能应用 第一章 Object-XML 映射简介 基础 将对象映射到 XML 一词意味着定义如何将该对象用作 XML 文档。要将对象映射到 XML,请将 %XML.Adaptor 添加到定义该对象的类的超…...

精密设备企业适合哪款CRM客户管理体系?
精密设备企业致力于打造现代化管理体系,以精密的仪器、精细的销售、精准的市场、精确的售后为企业核心,提供优质的精密产品和专业服务。随着企业的发展及市场发展需要,建立高效的客户关系管理体系势在必行。那么,精密设备企业适合…...

Rasa-笔记
1 Rasa环境搭建 笔者使用的Rasa版本是古早的1.10.7,python环境3.7。 1、安装miniconda 2、conda创建python3.7环境 3、安装TensorFlow和GPU相关 4、安装Rasa相关 2 Rasa笔记 3 Rasa报错 3.1 ValueError: Can’t patch loop of type <class ‘uvloop.Loop’&g…...
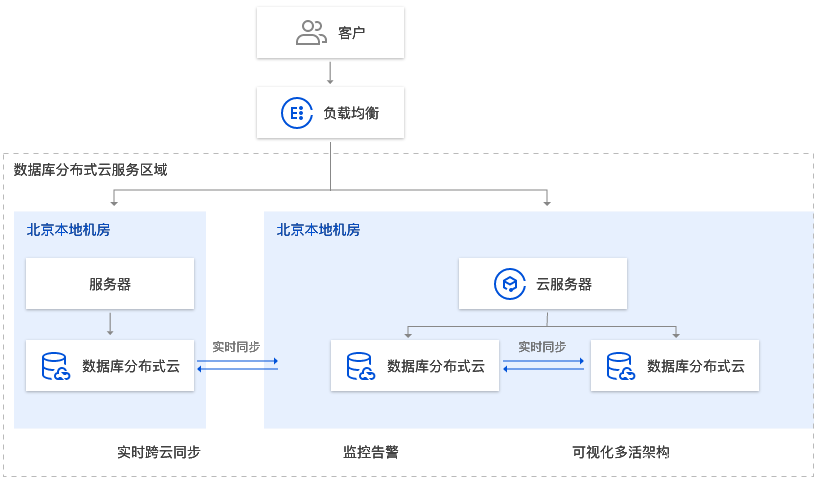
云架构师学习------腾讯云通识-存储与数据库
云架构师学习------腾讯云通识-存储与数据库 云架构师学习------腾讯云通识-存储与数据库存储基础存储服务对象存储-COS产品概述功能概览产品优势 云硬盘-CBS产品概述产品功能产品优势云硬盘类型 文件存储-CFS产品概述产品功能产品优势文件存储类型及性能规格存储类型性能与规格…...

蓝桥杯之模拟与枚举day1
Question1卡片(C/CA组第一题) 这个是一道简单的模拟枚举题目,只要把对应每次的i的各个位都提取出来,然后对应的卡片数目减去1即可。属于打卡题目。注意for循环的特殊使用即可 #include <iostream> using namespace std; bool solve(int a[],int n…...
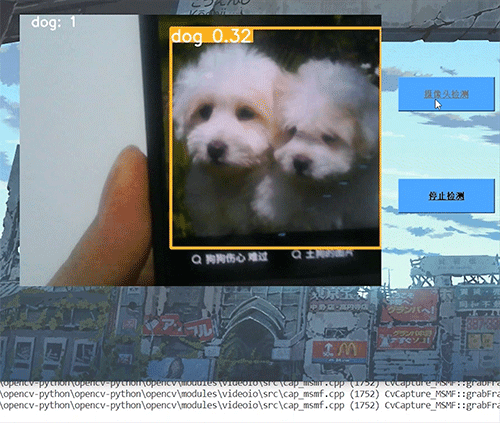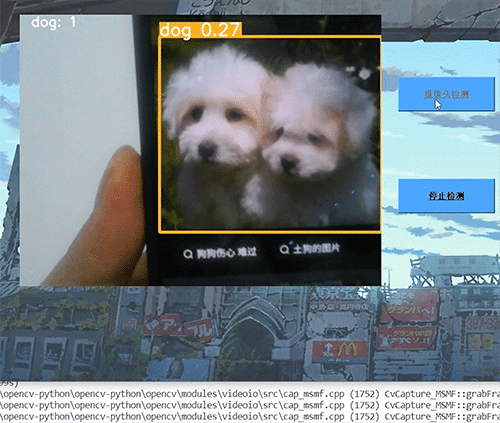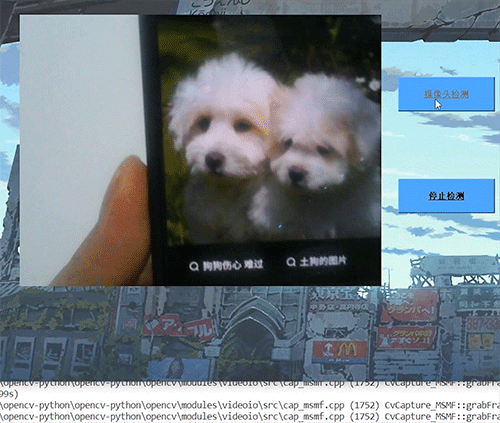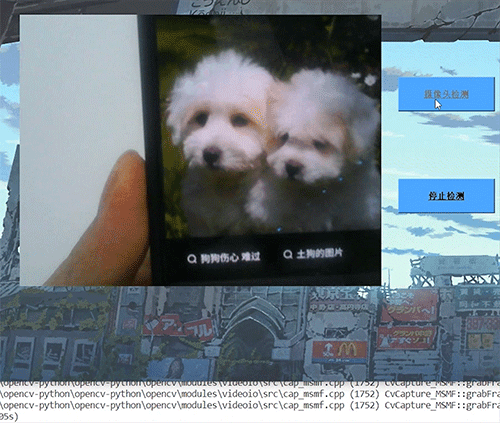
深度学习 python opencv 动物识别与检测 计算机竞赛
文章目录 0 前言1 深度学习实现动物识别与检测2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存…...
爱家房产网站源码 爱家房产网商业版 微信互动营销整合+手机触屏版+经纪人分销
房产网站源码手机访问自动转手机版修改修复如下: 1,修复手机版首页标题头部名称 2,修复手机版首页频道导航按钮 3,新增手机版广告位置显示方式 4,修复手机版首页内容显示样式 5,手机版头部背景颜色ic…...

招聘信息采集
首先,我们需要使用PHP的curl库来发送HTTP请求。以下是一个基本的示例: <?php // 初始化curl $ch curl_init();// 设置代理 curl_setopt($ch, CURLOPT_PROXY, "jshk.com.cn");// 设置URL curl_setopt($ch, CURLOPT_URL, "http://www…...

java开发宝典
Java命名规范 1:代码中的命名均不能以下划线或美元符号开始,也不能以下划线或美元符号结束。 反例:_name / __name / $name / name_ / name$ / name__ 。 2:禁止使用拼音和英文混合。 反例:DaZhePromotion [打折] / …...
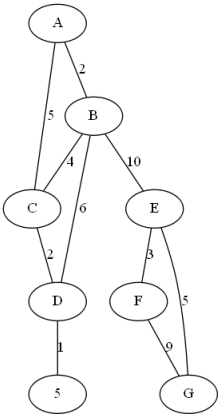
【图论实战】 Boost学习 03:dijkstra_shortest_paths
文章目录 示例代码 示例 最短路径: A -> C -> D -> F -> E -> G 长度 16 代码 #include <iostream> #include <boost/graph/adjacency_list.hpp> #include <boost/graph/dijkstra_shortest_paths.hpp> #include <boost/graph/graphviz.h…...

嵌入式养成计划-52----ARM--开发板介绍--相关硬件基础内容介绍--GPIO讲解
一百三十一、开发板介绍 131.1 核心板介绍 131.2 拓展板 一百三十二、相关硬件基础内容介绍 132.1 PCB PCB( Printed Circuit Board),中文名称为印制电路板,又称印刷线路板, 是重要的电子部件,是电子元器…...
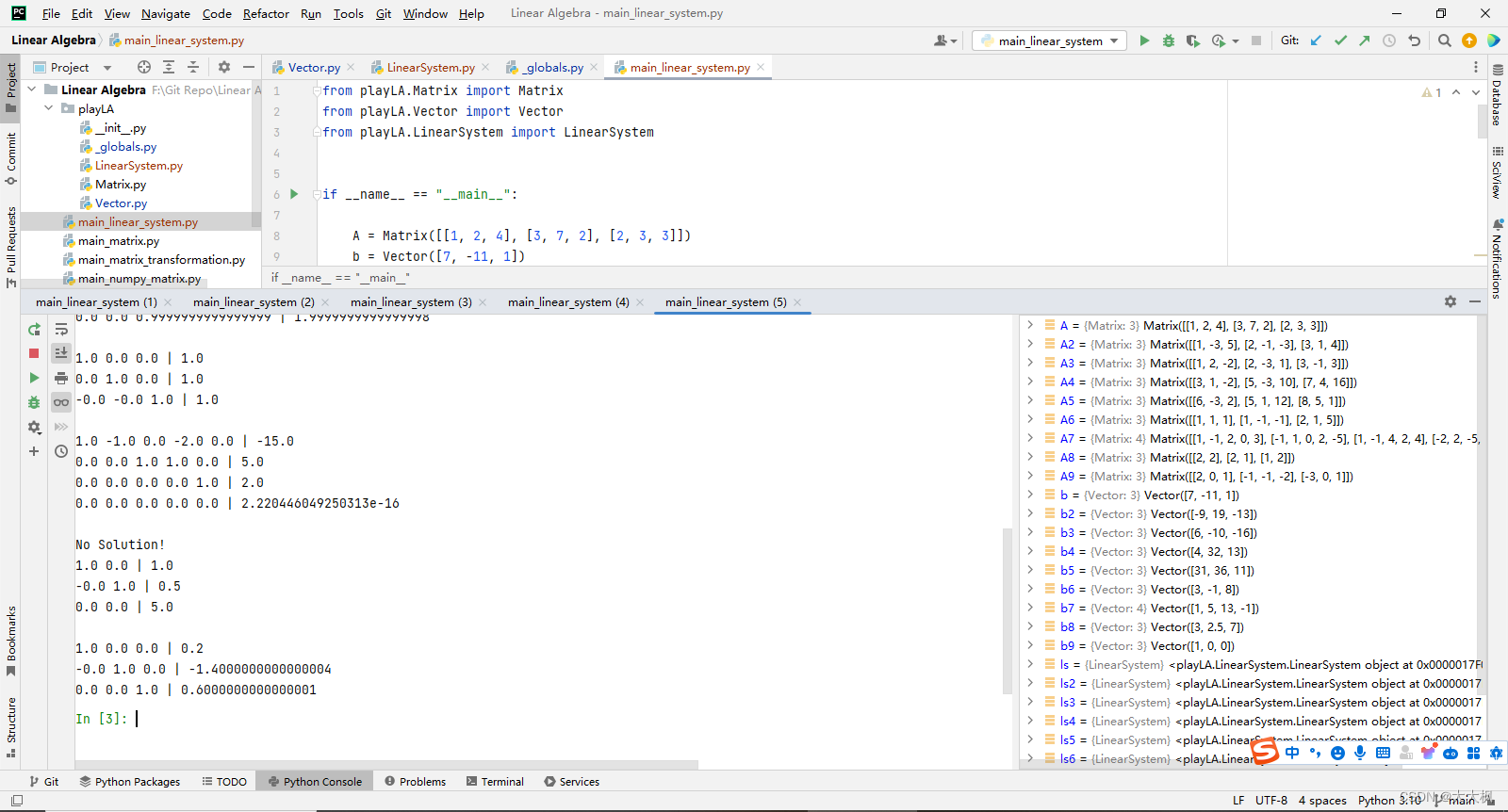
线性代数-Python-04:线性系统+高斯消元的实现
文章目录 1 线性系统2 高斯-jordon消元法的实现2.1 Matrix2.2 Vector2.3 线性系统 3 行最简形式4 线性方程组的结构5 线性方程组-通用高斯消元的实现5.1 global5.2 Vector-引入is_zero5.3 LinearSystem5.4 main 1 线性系统 2 高斯-jordon消元法的实现 2.1 Matrix from .Vecto…...

python能用来做什么
Python是一种流行的编程语言,由Guido van Rossum创建,并于1991年发布。 它用于: Web开发(服务器端); 软件开发,数学计算,系统脚本编写。 Python能做什么? Python可以…...

springboot引入外部jar,package打包报错找不到程序包XXX
springboot引入外包jar包有两种方法: 一、第一种: 点击idea左上角file,然后点击project选择Modules,点击右侧Dependencies,点击右侧加号选择JARs or directories,然后选择要导入的jar包。这种方式,引入ja…...
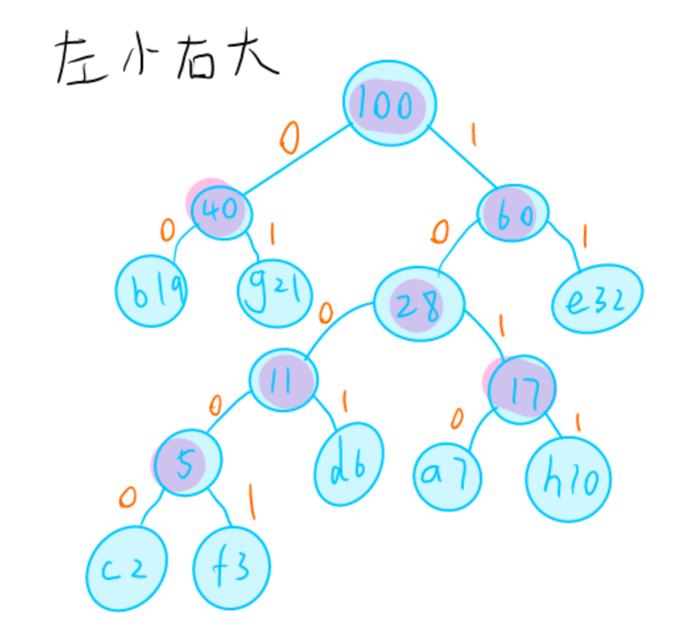
GDPU 数据结构 天码行空9
实验九 哈夫曼编码 一、【实验目的】 1、理解哈夫曼树的基本概念 2、掌握哈夫曼树的构造及数据结构设计 3、掌握哈夫曼编码问题设计和实现 二、【实验内容】 1、假设用于通信的电文仅由8个字母 {a, b, c, d, e, f, g, h} 构成,它们在电文中出现的概率分别为{ 0.…...
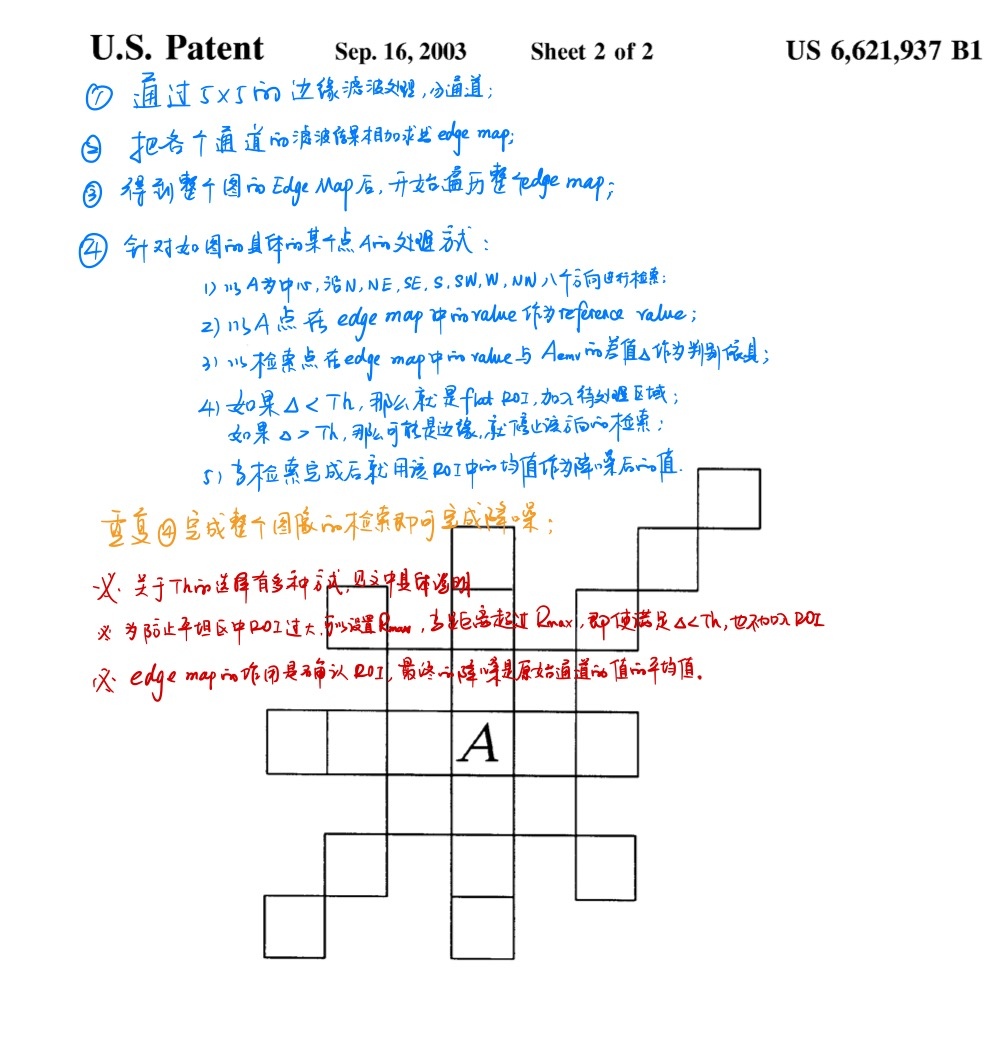
ISP算法——UVNR
ISP算法——UVNR 概念简介 UVNR也就是经过CSC只有在YUV域对UV两个色域进行降噪,在有些方案里也叫CNR(chroma noise reduction)。主要就是在YUV域针对彩燥进行特殊处理的一系列算法。 关于噪声产生的原因在前面关于降噪的文章和视频中已经做…...

双十一“静悄悄”?VR购物拉满沉浸式购物体验
以往每年的双十一,都会因为电商购物狂欢而变得热闹非凡,而各大电商平台也会在这天推出各种促销活动。但是,近几年来,双十一正在变得“静悄悄”。一个原因是消费群体越发理性消费,更加重视商品本身的质量和体验…...

(动手学习深度学习)第13章 计算机视觉---图像增广与微调
13.1 图像增广 总结 数据增广通过变形数据来获取多样性从而使得模型泛化性能更好常见图片增广包裹翻转、切割、变色。 图像增广代码实现...

Linux安装MySQL8.0服务
Linux安装MySQL8.0服务 文章目录 Linux安装MySQL8.0服务一、卸载1.1 查看mariadb1.2 卸载 二、安装2.1 下载2.2 上传2.3 解压2.4 重命名2.5 删除2.6 创建目录2.7 环境变量2.8 修改配置2.9 配置文件2.9 用户与用户组2.10 初始化2.11 其它 三、开启远程连接MySQL 一、卸载 首先第…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...
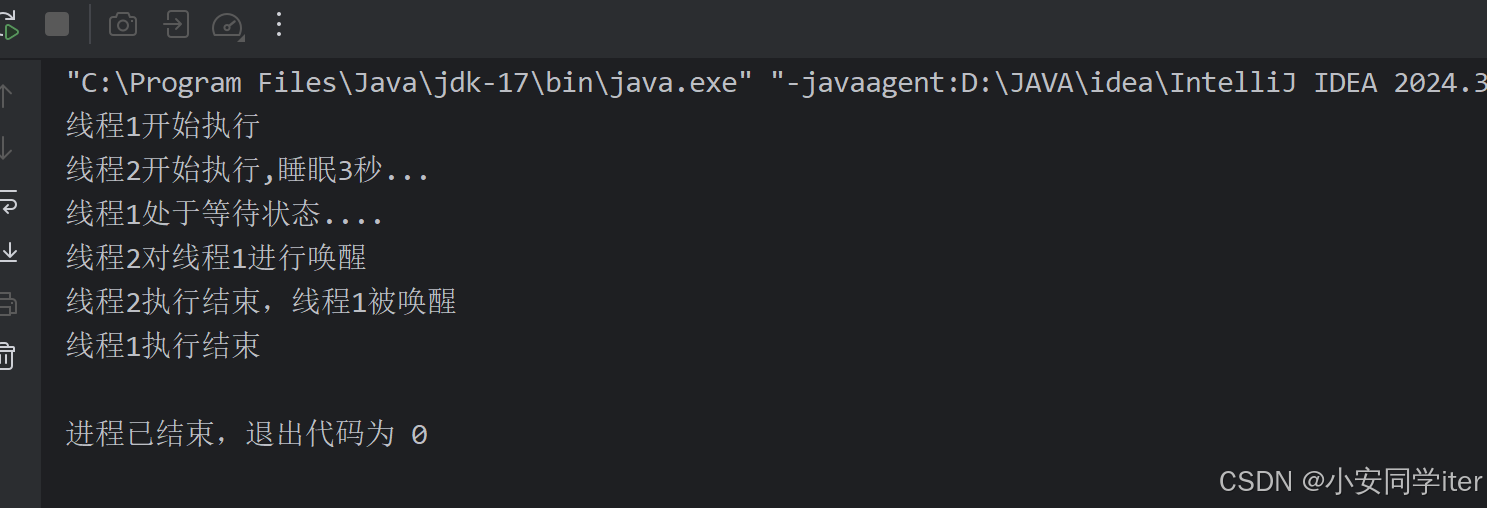
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...

第6章:Neo4j数据导入与导出
在实际应用中,数据的导入与导出是使用Neo4j的重要环节。无论是初始数据加载、系统迁移还是数据备份,都需要高效可靠的数据传输机制。本章将详细介绍Neo4j中的各种数据导入与导出方法,帮助读者掌握不同场景下的最佳实践。 6.1 数据导入策略 …...
