线性代数-Python-04:线性系统+高斯消元的实现
文章目录
- 1 线性系统
- 2 高斯-jordon消元法的实现
- 2.1 Matrix
- 2.2 Vector
- 2.3 线性系统
- 3 行最简形式
- 4 线性方程组的结构
- 5 线性方程组-通用高斯消元的实现
- 5.1 global
- 5.2 Vector-引入is_zero
- 5.3 LinearSystem
- 5.4 main
1 线性系统
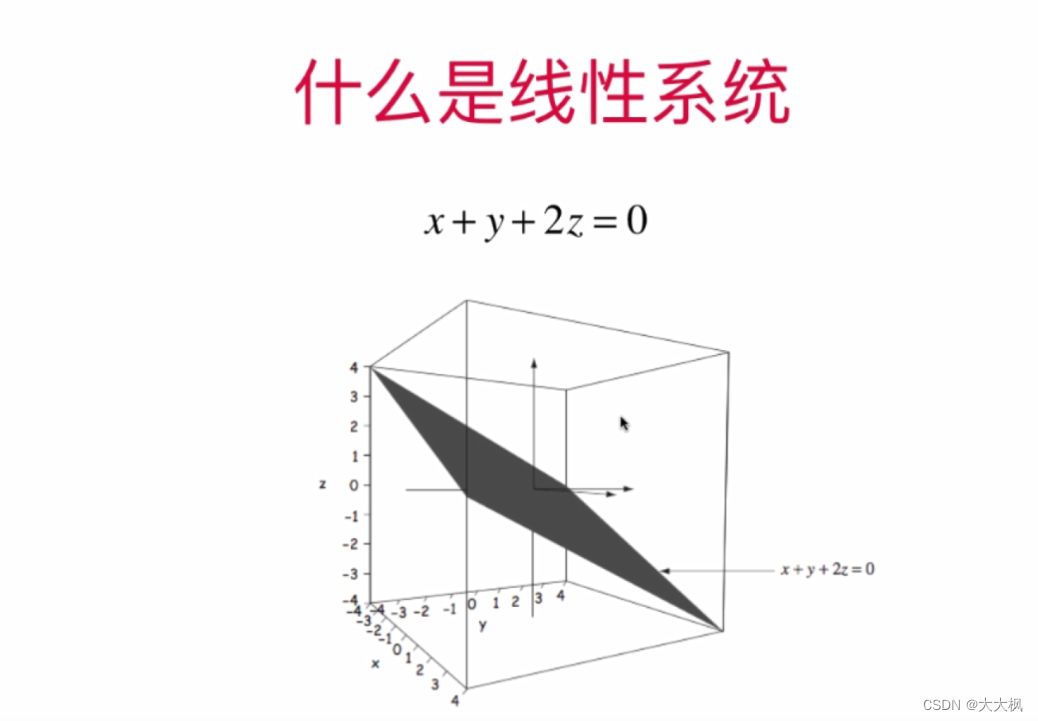
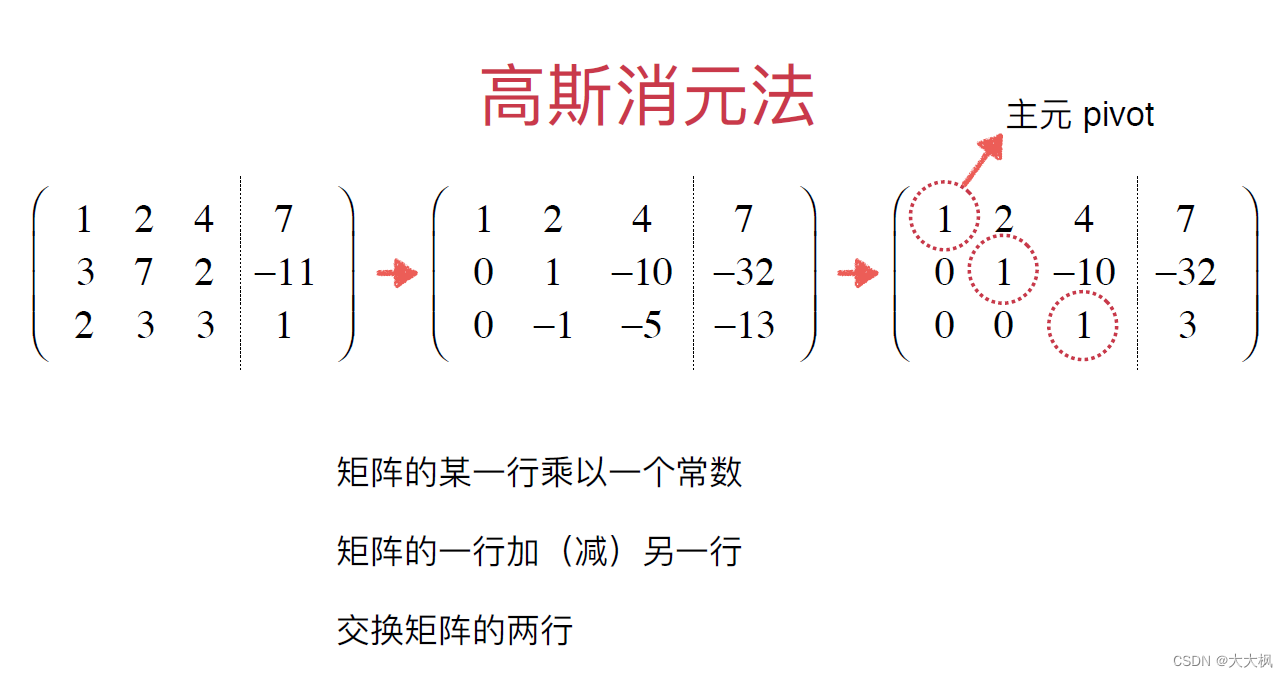
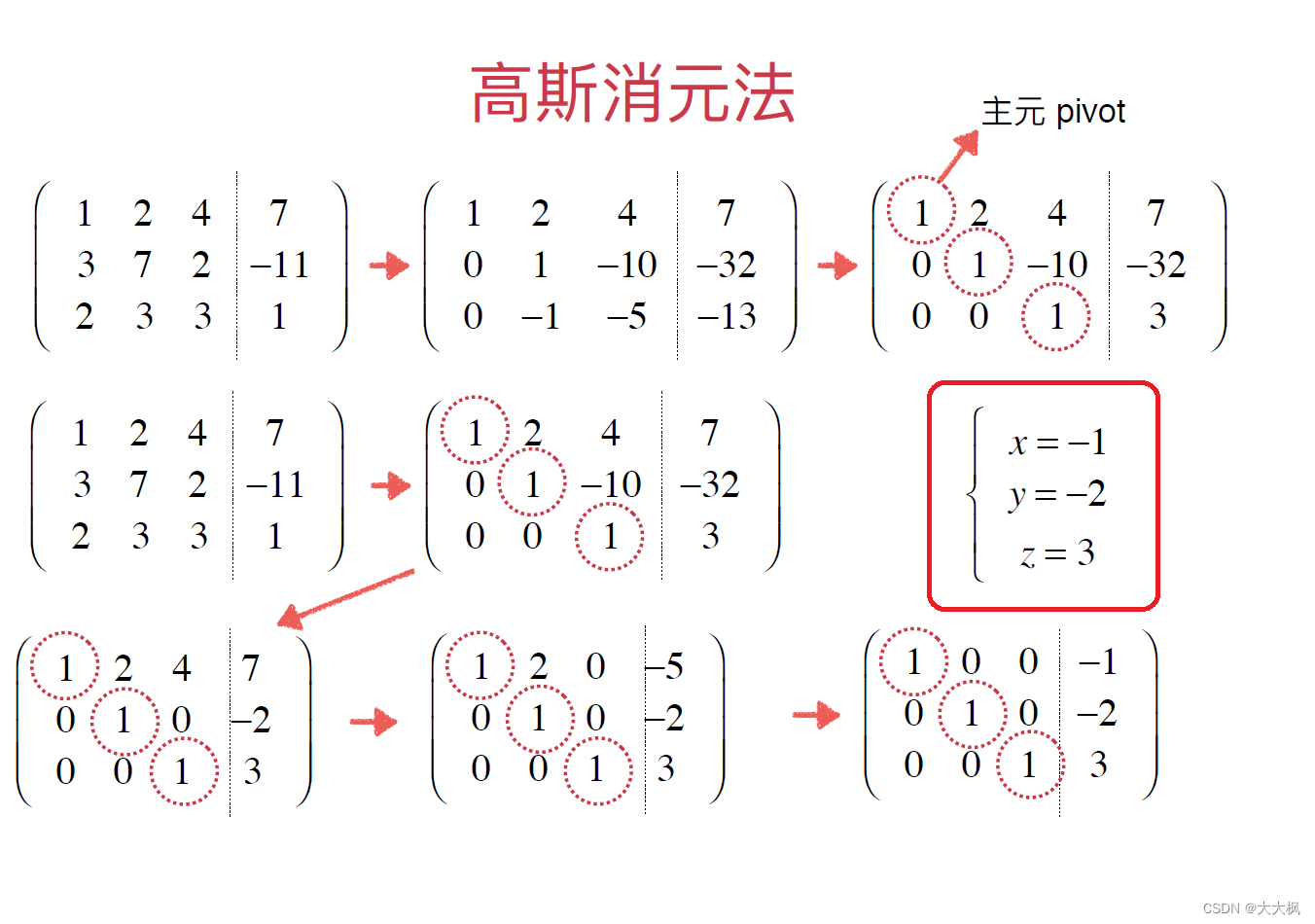
2 高斯-jordon消元法的实现
2.1 Matrix
from .Vector import Vectorclass Matrix:def __init__(self, list2d):self._values = [row[:] for row in list2d]@classmethoddef zero(cls, r, c):"""返回一个r行c列的零矩阵"""return cls([[0] * c for _ in range(r)])@classmethoddef identity(cls, n):"""返回一个n行n列的单位矩阵"""m = [[0]*n for _ in range(n)]for i in range(n):m[i][i] = 1;return cls(m)def T(self):"""返回矩阵的转置矩阵"""return Matrix([[e for e in self.col_vector(i)]for i in range(self.col_num())])def __add__(self, another):"""返回两个矩阵的加法结果"""assert self.shape() == another.shape(), \"Error in adding. Shape of matrix must be same."return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __sub__(self, another):"""返回两个矩阵的减法结果"""assert self.shape() == another.shape(), \"Error in subtracting. Shape of matrix must be same."return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def dot(self, another):"""返回矩阵乘法的结果"""if isinstance(another, Vector):# 矩阵和向量的乘法assert self.col_num() == len(another), \"Error in Matrix-Vector Multiplication."return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])if isinstance(another, Matrix):# 矩阵和矩阵的乘法assert self.col_num() == another.row_num(), \"Error in Matrix-Matrix Multiplication."return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())]for i in range(self.row_num())])def __mul__(self, k):"""返回矩阵的数量乘结果: self * k"""return Matrix([[e * k for e in self.row_vector(i)]for i in range(self.row_num())])def __rmul__(self, k):"""返回矩阵的数量乘结果: k * self"""return self * kdef __truediv__(self, k):"""返回数量除法的结果矩阵:self / k"""return (1 / k) * selfdef __pos__(self):"""返回矩阵取正的结果"""return 1 * selfdef __neg__(self):"""返回矩阵取负的结果"""return -1 * selfdef row_vector(self, index):"""返回矩阵的第index个行向量"""return Vector(self._values[index])def col_vector(self, index):"""返回矩阵的第index个列向量"""return Vector([row[index] for row in self._values])def __getitem__(self, pos):"""返回矩阵pos位置的元素"""r, c = posreturn self._values[r][c]def size(self):"""返回矩阵的元素个数"""r, c = self.shape()return r * cdef row_num(self):"""返回矩阵的行数"""return self.shape()[0]__len__ = row_numdef col_num(self):"""返回矩阵的列数"""return self.shape()[1]def shape(self):"""返回矩阵的形状: (行数, 列数)"""return len(self._values), len(self._values[0])def __repr__(self):return "Matrix({})".format(self._values)__str__ = __repr__2.2 Vector
import math
from ._globals import EPSILON
class Vector:def __init__(self, lst):"""__init__ 代表类的构造函数双下划线开头的变量 例如_values,代表类的私有成员lst是个引用,list(lst)将值复制一遍,防止用户修改值"""self._values = list(lst)def underlying_list(self):"""返回向量的底层列表"""return self._values[:]def dot(self, another):"""向量点乘,返回结果标量"""assert len(self) == len(another), \"Error in dot product. Length of vectors must be same."return sum(a * b for a, b in zip(self, another))def norm(self):"""返回向量的模"""return math.sqrt(sum(e**2 for e in self))def normalize(self):"""归一化,规范化返回向量的单位向量此处设计到了除法: def __truediv__(self, k):"""if self.norm() < EPSILON:raise ZeroDivisionError("Normalize error! norm is zero.")return Vector(self._values) / self.norm()# return 1 / self.norm() * Vector(self._values)# return Vector([e / self.norm() for e in self])def __truediv__(self, k):"""返回数量除法的结果向量:self / k"""return (1 / k) * self@classmethoddef zero(cls, dim):"""返回一个dim维的零向量@classmethod 修饰符对应的函数不需要实例化,不需要 self 参数,但第一个参数需要是表示自身类的cls参数,可以来调用类的属性,类的方法,实例化对象等。"""return cls([0] * dim)def __add__(self, another):"""向量加法,返回结果向量"""assert len(self) == len(another), \"Error in adding. Length of vectors must be same."# return Vector([a + b for a, b in zip(self._values, another._values)])return Vector([a + b for a, b in zip(self, another)])def __sub__(self, another):"""向量减法,返回结果向量"""assert len(self) == len(another), \"Error in subtracting. Length of vectors must be same."return Vector([a - b for a, b in zip(self, another)])def __mul__(self, k):"""返回数量乘法的结果向量:self * k"""return Vector([k * e for e in self])def __rmul__(self, k):"""返回数量乘法的结果向量:k * selfself本身就是一个列表"""return self * kdef __pos__(self):"""返回向量取正的结果向量"""return 1 * selfdef __neg__(self):"""返回向量取负的结果向量"""return -1 * selfdef __iter__(self):"""返回向量的迭代器"""return self._values.__iter__()def __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量长度(有多少个元素)"""return len(self._values)def __repr__(self):"""打印显示:Vector([5, 2])"""return "Vector({})".format(self._values)def __str__(self):"""打印显示:(5, 2)"""return "({})".format(", ".join(str(e) for e in self._values))
2.3 线性系统
from .Matrix import Matrix
from .Vector import Vectorclass LinearSystem:def __init__(self, A, b):assert A.row_num() == len(b), "row number of A must be equal to the length of b"self._m = A.row_num()self._n = A.col_num()assert self._m == self._n # TODO: no this restrictionself.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]])for i in range(self._m)]def _max_row(self, index_i, index_j, n):best, ret = abs(self.Ab[index_i][index_j]), index_ifor i in range(index_i + 1, n):if abs(self.Ab[i][index_j]) > best:best, ret = abs(self.Ab[i][index_j]), ireturn retdef _forward(self):n = self._mfor i in range(n):# Ab[i][i]为主元max_row = self._max_row(i, i, n)self.Ab[i], self.Ab[max_row] = self.Ab[max_row], self.Ab[i]# 将主元归为一self.Ab[i] = self.Ab[i] / self.Ab[i][i] # TODO: self.Ab[i][i] == 0?for j in range(i + 1, n):self.Ab[j] = self.Ab[j] - self.Ab[j][i] * self.Ab[i]def _backward(self):n = self._mfor i in range(n - 1, -1, -1):# Ab[i][i]为主元for j in range(i - 1, -1, -1):self.Ab[j] = self.Ab[j] - self.Ab[j][i] * self.Ab[i]def gauss_jordan_elimination(self):self._forward()self._backward()def fancy_print(self):for i in range(self._m):print(" ".join(str(self.Ab[i][j]) for j in range(self._n)), end=" ")print("|", self.Ab[i][-1])3 行最简形式
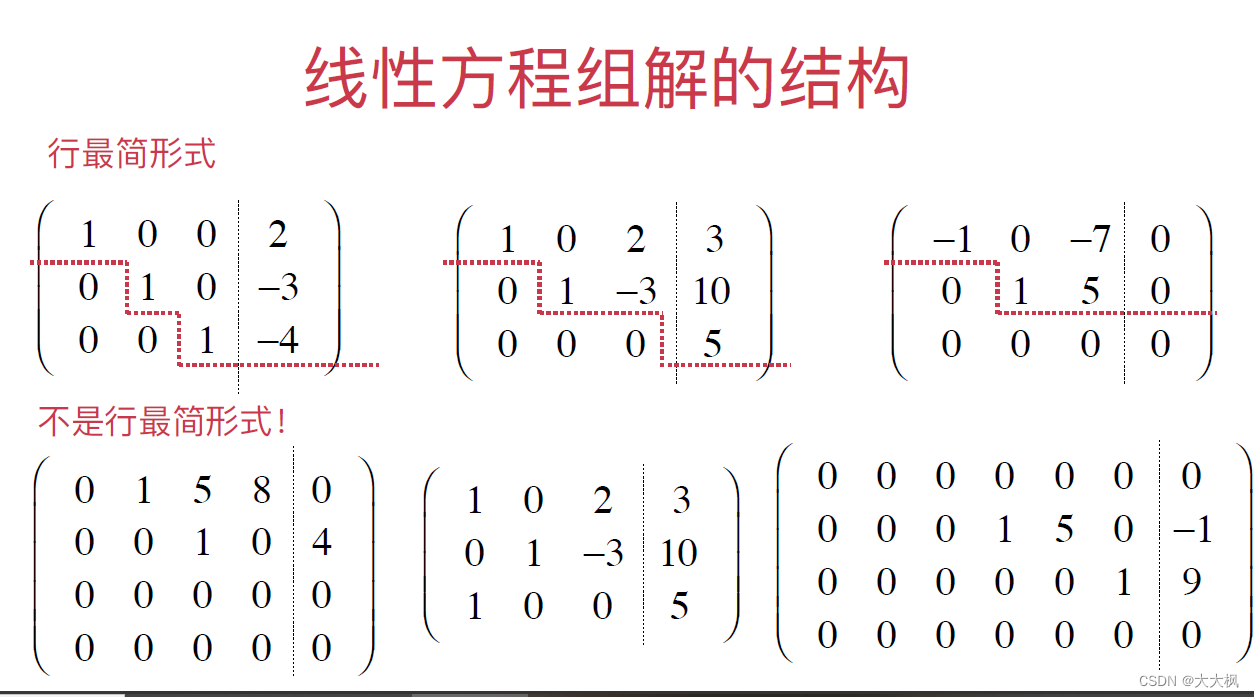
4 线性方程组的结构
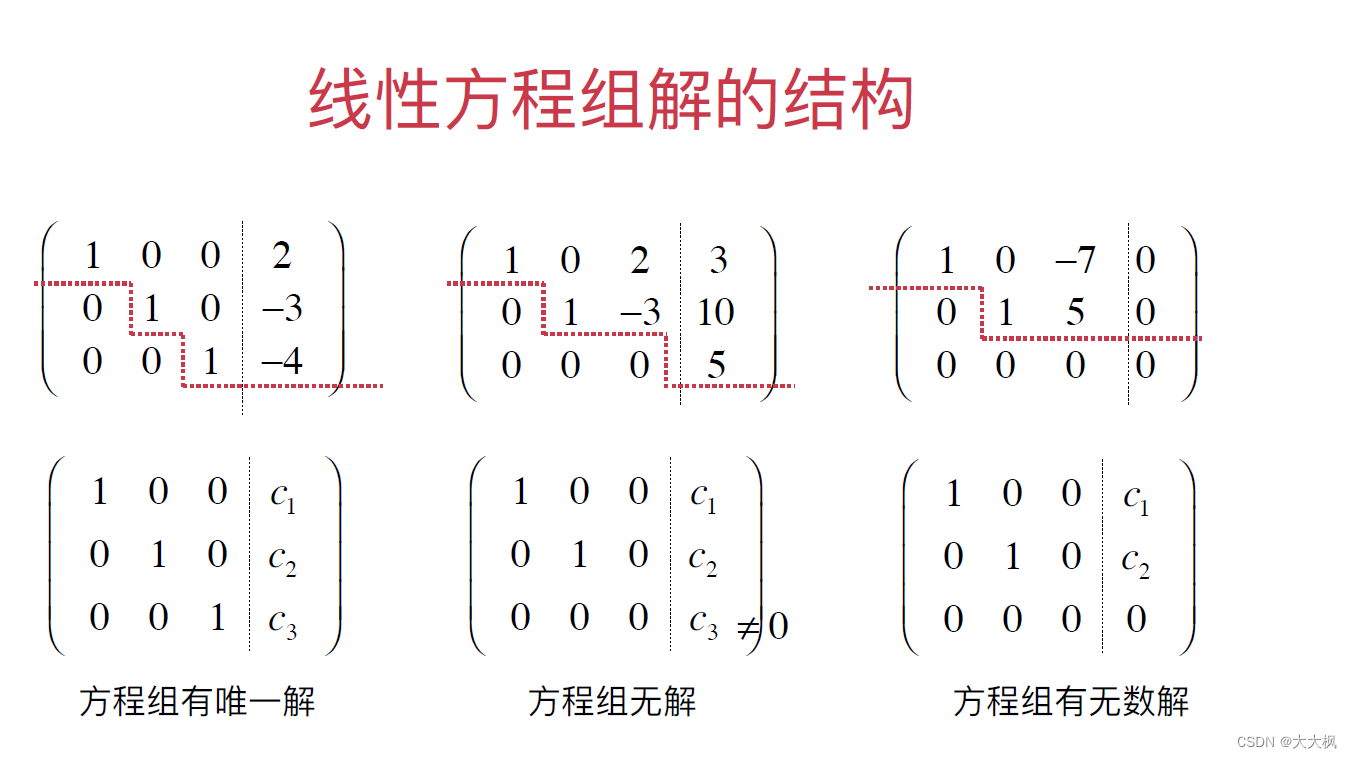
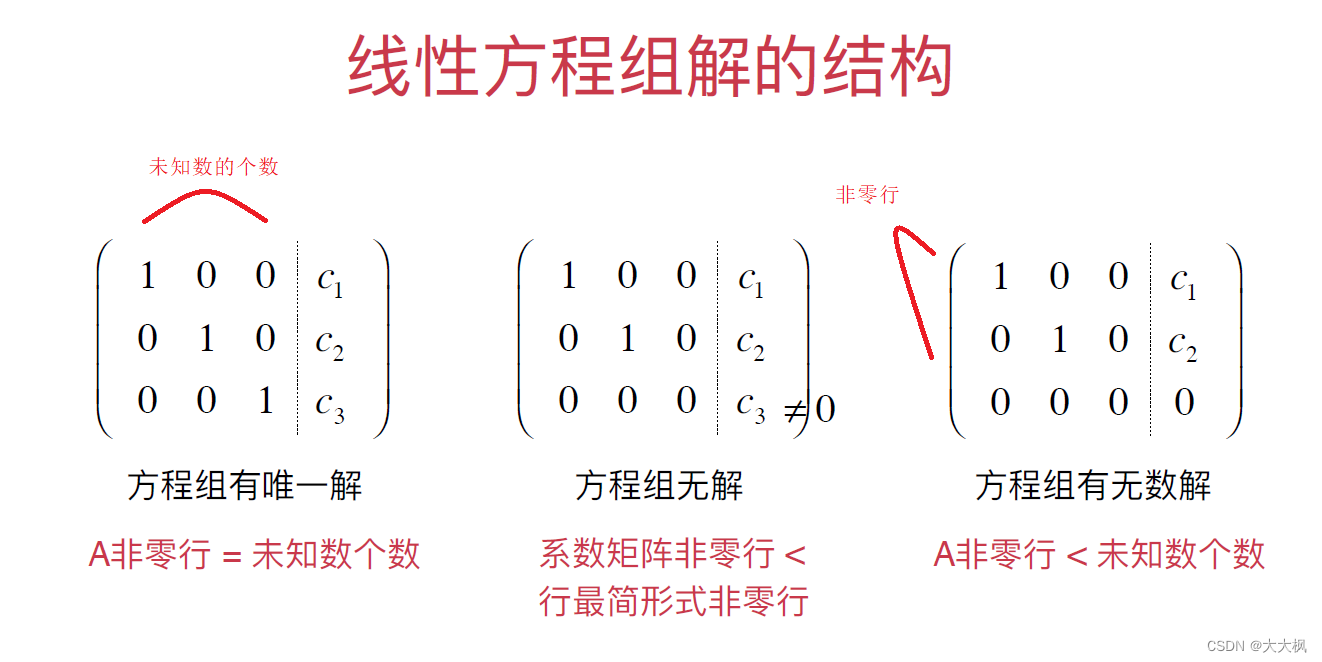
5 线性方程组-通用高斯消元的实现
5.1 global
# 包中的变量,但是对包外不可见,因此使用“_”开头
EPSILON = 1e-8def is_zero(x):return abs(x) < EPSILONdef is_equal(a, b):return abs(a - b) < EPSILON
5.2 Vector-引入is_zero
import math
from ._globals import is_zero
class Vector:def __init__(self, lst):"""__init__ 代表类的构造函数双下划线开头的变量 例如_values,代表类的私有成员lst是个引用,list(lst)将值复制一遍,防止用户修改值"""self._values = list(lst)def underlying_list(self):"""返回向量的底层列表"""return self._values[:]def dot(self, another):"""向量点乘,返回结果标量"""assert len(self) == len(another), \"Error in dot product. Length of vectors must be same."return sum(a * b for a, b in zip(self, another))def norm(self):"""返回向量的模"""return math.sqrt(sum(e**2 for e in self))def normalize(self):"""归一化,规范化返回向量的单位向量此处设计到了除法: def __truediv__(self, k):"""if is_zero(self.norm()):raise ZeroDivisionError("Normalize error! norm is zero.")return Vector(self._values) / self.norm()# return 1 / self.norm() * Vector(self._values)# return Vector([e / self.norm() for e in self])def __truediv__(self, k):"""返回数量除法的结果向量:self / k"""return (1 / k) * self@classmethoddef zero(cls, dim):"""返回一个dim维的零向量@classmethod 修饰符对应的函数不需要实例化,不需要 self 参数,但第一个参数需要是表示自身类的cls参数,可以来调用类的属性,类的方法,实例化对象等。"""return cls([0] * dim)def __add__(self, another):"""向量加法,返回结果向量"""assert len(self) == len(another), \"Error in adding. Length of vectors must be same."# return Vector([a + b for a, b in zip(self._values, another._values)])return Vector([a + b for a, b in zip(self, another)])def __sub__(self, another):"""向量减法,返回结果向量"""assert len(self) == len(another), \"Error in subtracting. Length of vectors must be same."return Vector([a - b for a, b in zip(self, another)])def __mul__(self, k):"""返回数量乘法的结果向量:self * k"""return Vector([k * e for e in self])def __rmul__(self, k):"""返回数量乘法的结果向量:k * selfself本身就是一个列表"""return self * kdef __pos__(self):"""返回向量取正的结果向量"""return 1 * selfdef __neg__(self):"""返回向量取负的结果向量"""return -1 * selfdef __iter__(self):"""返回向量的迭代器"""return self._values.__iter__()def __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量长度(有多少个元素)"""return len(self._values)def __repr__(self):"""打印显示:Vector([5, 2])"""return "Vector({})".format(self._values)def __str__(self):"""打印显示:(5, 2)"""return "({})".format(", ".join(str(e) for e in self._values))
5.3 LinearSystem
from .Matrix import Matrix
from .Vector import Vector
from ._globals import is_zeroclass LinearSystem:def __init__(self, A, b):assert A.row_num() == len(b), "row number of A must be equal to the length of b"self._m = A.row_num()self._n = A.col_num()# assert self._m == self._n # TODO: no this restrictionself.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]])for i in range(self._m)]self.pivots = []def _max_row(self, index_i, index_j, n):best, ret = abs(self.Ab[index_i][index_j]), index_ifor i in range(index_i + 1, n):if abs(self.Ab[i][index_j]) > best:best, ret = abs(self.Ab[i][index_j]), ireturn retdef _forward(self):i, k = 0, 0while i < self._m and k < self._n:# 看Ab[i][k]位置是否可以是主元max_row = self._max_row(i, k, self._m)self.Ab[i], self.Ab[max_row] = self.Ab[max_row], self.Ab[i]if is_zero(self.Ab[i][k]):k += 1else:# 将主元归为一self.Ab[i] = self.Ab[i] / self.Ab[i][k]for j in range(i + 1, self._m):self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]self.pivots.append(k)i += 1def _backward(self):n = len(self.pivots)for i in range(n - 1, -1, -1):k = self.pivots[i]# Ab[i][k]为主元for j in range(i - 1, -1, -1):self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]def gauss_jordan_elimination(self):"""如果有解,返回True;如果没有解,返回False"""self._forward()self._backward()for i in range(len(self.pivots), self._m):if not is_zero(self.Ab[i][-1]):return Falsereturn Truedef fancy_print(self):for i in range(self._m):print(" ".join(str(self.Ab[i][j]) for j in range(self._n)), end=" ")print("|", self.Ab[i][-1])5.4 main
from playLA.Matrix import Matrix
from playLA.Vector import Vector
from playLA.LinearSystem import LinearSystemif __name__ == "__main__":A = Matrix([[1, 2, 4], [3, 7, 2], [2, 3, 3]])b = Vector([7, -11, 1])ls = LinearSystem(A, b)ls.gauss_jordan_elimination()ls.fancy_print()print()# [-1, -2, 3]A2 = Matrix([[1, -3, 5], [2, -1, -3], [3, 1, 4]])b2 = Vector([-9, 19, -13])ls2 = LinearSystem(A2, b2)ls2.gauss_jordan_elimination()ls2.fancy_print()print()# [2, -3, -4]A3 = Matrix([[1, 2, -2], [2, -3, 1], [3, -1, 3]])b3 = Vector([6, -10, -16])ls3 = LinearSystem(A3, b3)ls3.gauss_jordan_elimination()ls3.fancy_print()print()# [-2, 1, -3]A4 = Matrix([[3, 1, -2], [5, -3, 10], [7, 4, 16]])b4 = Vector([4, 32, 13])ls4 = LinearSystem(A4, b4)ls4.gauss_jordan_elimination()ls4.fancy_print()print()# [3, -4, 0.5]A5 = Matrix([[6, -3, 2], [5, 1, 12], [8, 5, 1]])b5 = Vector([31, 36, 11])ls5 = LinearSystem(A5, b5)ls5.gauss_jordan_elimination()ls5.fancy_print()print()# [3, -3, 2]A6 = Matrix([[1, 1, 1], [1, -1, -1], [2, 1, 5]])b6 = Vector([3, -1, 8])ls6 = LinearSystem(A6, b6)ls6.gauss_jordan_elimination()ls6.fancy_print()print()# [1, 1, 1]A7 = Matrix([[1, -1, 2, 0, 3],[-1, 1, 0, 2, -5],[1, -1, 4, 2, 4],[-2, 2, -5, -1, -3]])b7 = Vector([1, 5, 13, -1])ls7 = LinearSystem(A7, b7)ls7.gauss_jordan_elimination()ls7.fancy_print()print()A8 = Matrix([[2, 2],[2, 1],[1, 2]])b8 = Vector([3, 2.5, 7])ls8 = LinearSystem(A8, b8)if not ls8.gauss_jordan_elimination():print("No Solution!")ls8.fancy_print()print()A9 = Matrix([[2, 0, 1],[-1, -1, -2],[-3, 0, 1]])b9 = Vector([1, 0, 0])ls9 = LinearSystem(A9, b9)if not ls9.gauss_jordan_elimination():print("No Solution!")ls9.fancy_print()print()
相关文章:

线性代数-Python-04:线性系统+高斯消元的实现
文章目录 1 线性系统2 高斯-jordon消元法的实现2.1 Matrix2.2 Vector2.3 线性系统 3 行最简形式4 线性方程组的结构5 线性方程组-通用高斯消元的实现5.1 global5.2 Vector-引入is_zero5.3 LinearSystem5.4 main 1 线性系统 2 高斯-jordon消元法的实现 2.1 Matrix from .Vecto…...

python能用来做什么
Python是一种流行的编程语言,由Guido van Rossum创建,并于1991年发布。 它用于: Web开发(服务器端); 软件开发,数学计算,系统脚本编写。 Python能做什么? Python可以…...

springboot引入外部jar,package打包报错找不到程序包XXX
springboot引入外包jar包有两种方法: 一、第一种: 点击idea左上角file,然后点击project选择Modules,点击右侧Dependencies,点击右侧加号选择JARs or directories,然后选择要导入的jar包。这种方式,引入ja…...
GDPU 数据结构 天码行空9
实验九 哈夫曼编码 一、【实验目的】 1、理解哈夫曼树的基本概念 2、掌握哈夫曼树的构造及数据结构设计 3、掌握哈夫曼编码问题设计和实现 二、【实验内容】 1、假设用于通信的电文仅由8个字母 {a, b, c, d, e, f, g, h} 构成,它们在电文中出现的概率分别为{ 0.…...
ISP算法——UVNR
ISP算法——UVNR 概念简介 UVNR也就是经过CSC只有在YUV域对UV两个色域进行降噪,在有些方案里也叫CNR(chroma noise reduction)。主要就是在YUV域针对彩燥进行特殊处理的一系列算法。 关于噪声产生的原因在前面关于降噪的文章和视频中已经做…...

双十一“静悄悄”?VR购物拉满沉浸式购物体验
以往每年的双十一,都会因为电商购物狂欢而变得热闹非凡,而各大电商平台也会在这天推出各种促销活动。但是,近几年来,双十一正在变得“静悄悄”。一个原因是消费群体越发理性消费,更加重视商品本身的质量和体验…...

(动手学习深度学习)第13章 计算机视觉---图像增广与微调
13.1 图像增广 总结 数据增广通过变形数据来获取多样性从而使得模型泛化性能更好常见图片增广包裹翻转、切割、变色。 图像增广代码实现...

Linux安装MySQL8.0服务
Linux安装MySQL8.0服务 文章目录 Linux安装MySQL8.0服务一、卸载1.1 查看mariadb1.2 卸载 二、安装2.1 下载2.2 上传2.3 解压2.4 重命名2.5 删除2.6 创建目录2.7 环境变量2.8 修改配置2.9 配置文件2.9 用户与用户组2.10 初始化2.11 其它 三、开启远程连接MySQL 一、卸载 首先第…...
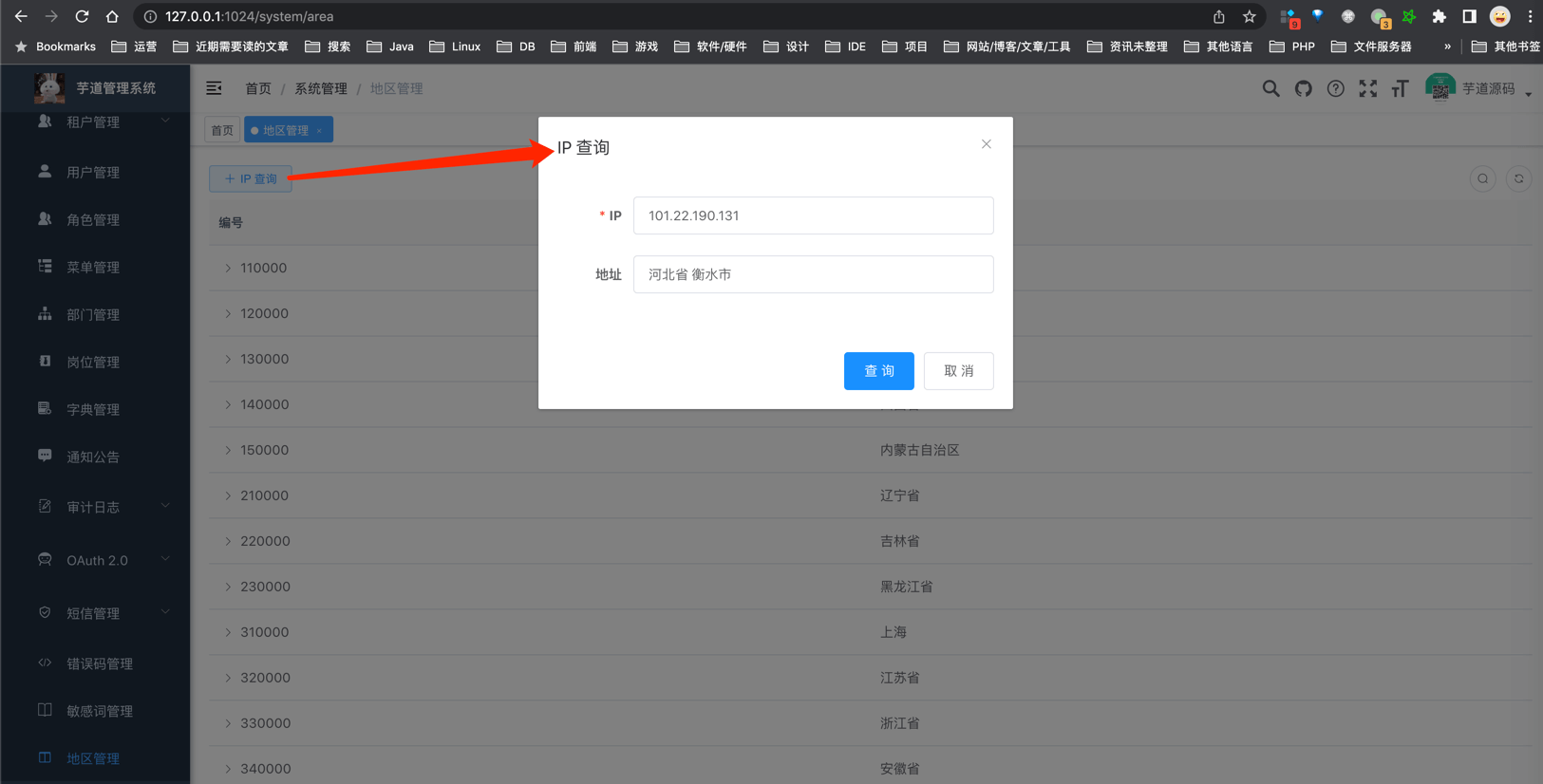
地区 IP 库
地区 & IP 库 yudao-spring-boot-starter-biz-ip (opens new window)业务组件,提供地区 & IP 库的封装。 #1. 地区 AreaUtils (opens new window)是地区工具类,可以查询中国的省、市、区县,也可以查询国外的国家。 它的数据来自 …...

MySQL查询语句练习题,测试基本够用了
1.创建student和score表 CREATE TABLE student ( id INT(10) NOT NULL UNIQUE PRIMARY KEY , name VARCHAR(20) NOT NULL , sex VARCHAR(4) , birth YEAR, department VARCHAR(20) , address VARCHAR(50) ); 创建score表。SQL代码如下: CREATE TA…...
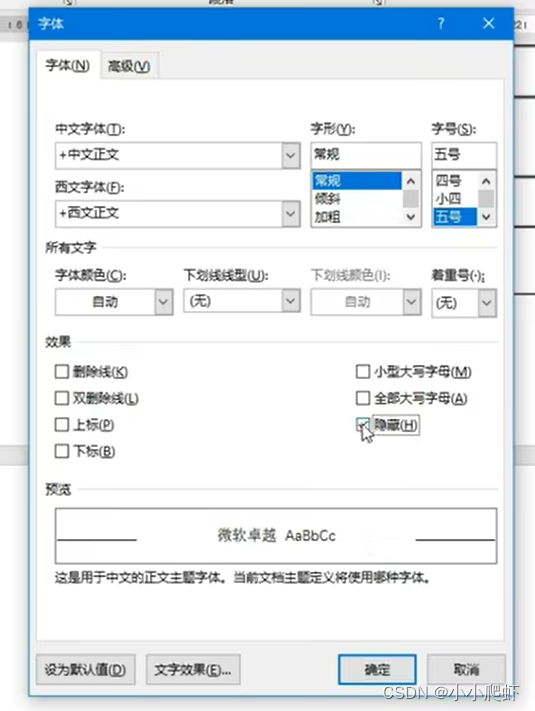
删除word最后一页之后的空白页
最近编辑word比较多,有时最后一页(最后一页内容还有可能是表格)之后,还有一页空白页,单独按下backspace、del都删不掉,很让人着急。 经过查询有几种方法: (1)点击选中空…...

基于站点、模式、遥感多源降水数据融合实践技术应用
降水在水循环中发挥着重要作用,塑造了生态景观和生态系统。目前,有四种主要方式获取降水数据:1)雨量计观测,2)地基雷达遥感,3)卫星遥感,4)模式模拟。基于雨量…...

html与django实现多级数据联动
html与django实现多级数据联动 1、流程 1、进入页面后先获取年级数据 2、选择年级后获取院级数据 3、选择院级后获取层次数据 4、选择层次数据后获取专业数据 2、html代码 <p style"margin-top: 10px;"><label>年级</label><select id"…...

网络安全-黑客技术-小白学习
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

.NET关于 跳过SSL中遇到的问题
一、事件的起因: 起因:开发项目过程中,可能会遇到 调用其他系统的接口 以及 代码中历史开发人员留下的IP接口访问等问题,后面该项目由自己负责,其他系统全部迁移到容器里面,只提供域名去访问。 问题:访问已迁移到容器其他系统,那么用IP地址访问肯定无法调用成功,只能用…...
fpga时序相关概念与理解
一、基本概念理解 对于数字系统而言,建立时间(setup time)和保持时间(hold time)是数字电路时序的基础。数字电路系统的稳定性,基本取决于时序是否满足建立时间和保持时间。 建立时间Tsu:触发器…...
)
安卓常见设计模式12------观察者模式(Kotlin版、Livedata、Flow)
1. W1 是什么,什么是观察者模式? 观察者模式(Observer Pattern)是一种行为型设计模式,用于实现组件间的松耦合通信。主要对象有观察者接口(Observer)和可观察对象(Observable&…...

USB偏好设置-Android13
USB偏好设置 1、USB偏好设置界面和入口2、USB功能设置2.1 USB功能对应模式2.2 点击设置2.3 广播监听刷新 3、日志开关3.1 Evet日志3.2 代码中日志开关3.3 关键日志 4、异常 1、USB偏好设置界面和入口 设置》已连接的设备》USB packages/apps/Settings/src/com/android/setting…...
 安装 libssl1.1)
Ubuntu 22.04 (WSL) 安装 libssl1.1
废话不多说!!! 步骤一: echo "deb http://security.ubuntu.com/ubuntu focal-security main" | sudo tee /etc/apt/sources.list.d/focal-security.list 步骤二: sudo apt-get update 步骤三:…...
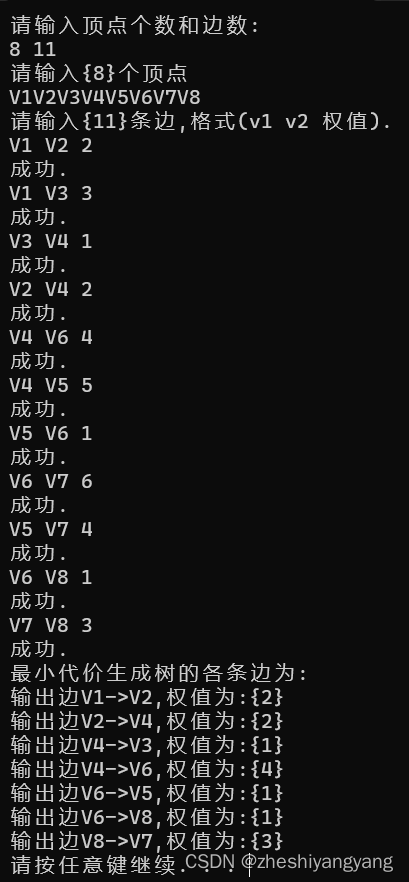
数据结构-图的课后习题(2)
题目要求: 对于下面的这个无向网,给出: 1.“深度优先搜索序列”(从V1开始) 2.“广度优先序列”(从V1开始) 3.“用Prim算法求最小生成树” 代码实现: 1.深度优先搜索:…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
