树之二叉排序树(二叉搜索树)
什么是排序树
说一下普通二叉树可不是左小右大的

插入的新节点是以叶子形式进行插入的
二叉排序树的中序遍历结果是一个升序的序列
下面是两个典型的二叉排序树


二叉排序树的操作
构造树的过程即是对无序序列进行排序的过程。

存储结构
通常采用二叉链表作为存储结构 不能

插入算法

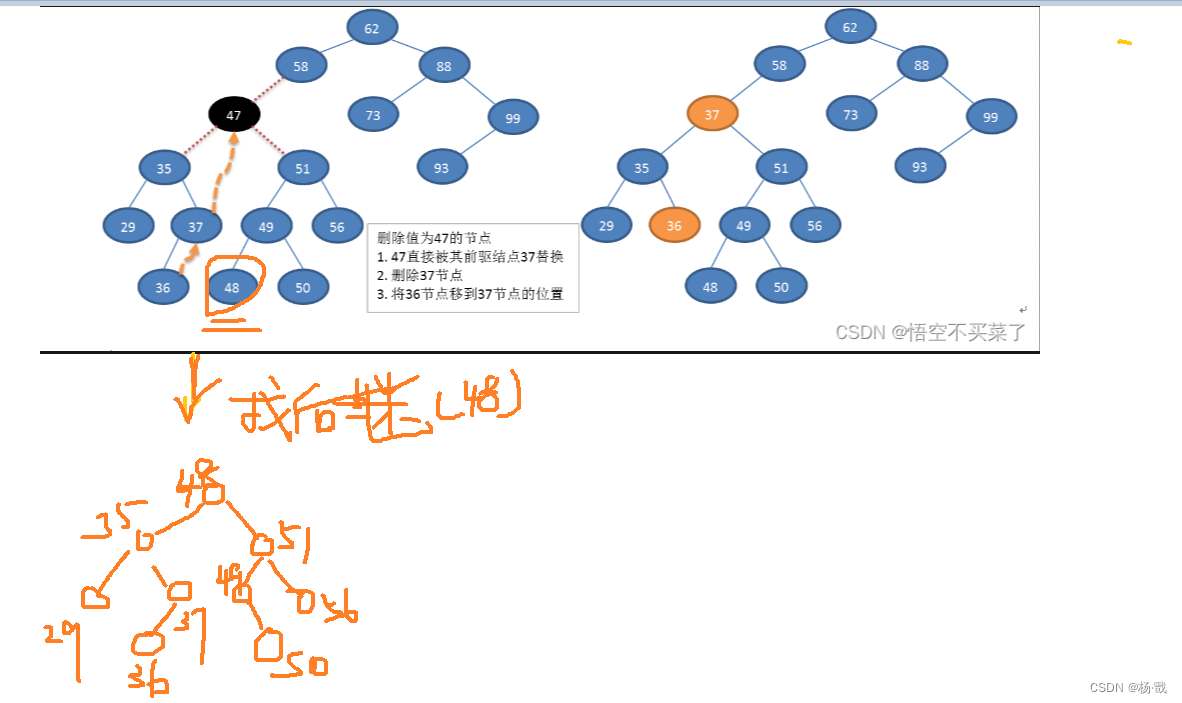
下面插入一个图解

上面的×就表示会在当前位置给delete掉一个结点
查找算法

删除算法



第三种情况:你删除的结点下面就是说还有左右子树,那么这个时候,我们就要去找到这棵树中序遍历结果之后的直接前驱或者直接后继,然后把这个前驱或者后继给按到删除结点这个位置上,将它下面的树移到被替换结点的位置

删除操作的具体讲解
重点讲解一下删除节点的核心分析

这里在补一张中序遍历的递归调用图

直接上代码
在上代码之前,先来说一下,二叉搜索树很多方法都利用了递归的思想,许多说明我都放到代码注释里面了,可以结合下面的这张图进行思维分析
先来看c语言代码(algorithm/bst/bst1.c)
#include <stdio.h>
#include <stdlib.h>typedef int key_type;
typedef struct _node
{key_type key;struct _node *left;struct _node *right;
}node, *pnode;void insert_bst(pnode *root, key_type key)
{//初始化插入结点pnode p = (pnode)malloc(sizeof(node));if (p != NULL){p->key = key;//把值给放进去p->left = p->right = NULL;}//空树的时候,直接作为根结点if (*root == NULL){*root = p;return;}//插入到当前结点的左孩子if ((*root)->left == NULL && (*root)->key > key){(*root)->left = p;//直接在堆上面指就可以了return;}//插入到当前结点的右孩子if ((*root)->right == NULL && (*root)->key < key){(*root)->right = p;return;}//上面都没有进入,说明结点就要往下继续存放//需要先把我们分配的结点内存给释放掉free(p);//左子树递归if ((*root)->key > key) {insert_bst(&(*root)->left, key);}//右子树递归else if((*root)->key < key) {insert_bst(&(*root)->right, key);}
}//根据关键字删除某个结点,成功返回1,失败返回0
int delete_bst(pnode *root, key_type key)
{if (*root == NULL){return 0;//这是一棵空树}if ((*root)->key == key){pnode pbak1, pmove;//判断右子树是否为空,为空,只需要重接左子树if ((*root)->right == NULL){//把当前结点的左子树接上去就可以了pbak1 = *root;//当前结点备份等会释放//改变在栈上面一级指针的指向*root = (*root)->left;//删除free(pbak1); }//左子树为空的情况下,只需要重接右子树就行了else if ((*root)->left == NULL){//删除结点的空间备份pbak1 = *root;*root = (*root)->right;//改变栈上结点的指向free(pbak1);}//左右子树都不为空else{//我们要找到直接前驱或者一个直接后继//前驱就是当前结点下一个结点左边结点的右边(尽头),所以先把root指向了左结点pbak1 = *root;//删除结点的一个备份pmove = (*root)->left;//左边等会要接接上//再来循环右边//注意的问题是我们需要指向一个直接前驱的父结点//以便于用来更改当前的子树结点,也就是被删除结点的下一个结点要连接上去while (pmove->right){pbak1 = pmove;//前驱结点的父节点pmove = pmove->right;//这个是指向了我们需要的前驱结点}//s指向了前驱结点,将s放到root结点上面(*root)->key = pmove->key;//改变了值,不是地址,等会吧pmove给释放掉//重接一下下面结点的子树//如果pbak1没有移动过,那么pbak1->left = pmove ->left;if (pbak1 == *root){pbak1->left = pmove->left;}else {//如果移动过,那么pbak1->right就要改变pbak1->right = pmove->left;}//释放掉pmove这个结点free(pmove);}return 1;}//没有找到的情况下,我们需要遍历树else if (key < (*root)->key) {//直接走左子树//这里必须return ,不然找到了也会falsereturn delete_bst(&(*root)->left, key);}else if (key > (*root)->key){//大于当前结点就直接走右子树return delete_bst(&(*root)->right, key);}return 0;
}//查找元素,找到返回结点指针,没找到返回NULL
//找结点,传入一个一级指针就好了
pnode search_bst(pnode root, key_type key)
{if (root == NULL){return NULL;}//查找右子树if (key > root->key){return search_bst(root->right, key);}//查找左子树else if (key < root->key){return search_bst(root->left, key);}else {return root;}
}//查找最小的关键字,空树时返回NULL
pnode search_min_bst(pnode root)
{if (root == NULL){return NULL;}//最小的话应该就是最左边孩子if (root->left == NULL){return root;//叶子结点下面都是NULL}else {return search_min_bst(root->left);}
}//查找最大关键字,空树时返回NULL
pnode search_max_bst(pnode root)
{if (root == NULL){return NULL;}//找到最后的孩子if (root->right == NULL){return root;}else{//一直往右边找,直到没有有孩子结点return search_max_bst(root->right);}
}//中序遍历二叉树
void inorder_traverse_bst(pnode root)
{if (root != NULL){//遍历左子树//先走到最左边,依次调用结束,返回打印inorder_traverse_bst(root->left);//走到最后一个结束,打印,中间根结点也会打印printf("%d ", root->key);//然后走右边开始打印inorder_traverse_bst(root->right);}
}int main()
{//创建一棵二叉树pnode root = NULL;insert_bst(&root, 3);insert_bst(&root, 8);insert_bst(&root, 2);insert_bst(&root, 5);insert_bst(&root, 4);insert_bst(&root, 9);insert_bst(&root, 11);//中序遍历二叉树inorder_traverse_bst(root);delete_bst(&root, 2);printf("\n---------------------\n");inorder_traverse_bst(root);return 0;
}再来看java的运行代码(algorithm/bst1)
package com.pxx.tree.bst1;
class Node {int key;Node left, right;//这里就是在new的时候可以出初始化一个头结点public Node(int key) {this.key = key;this.left = this.right = null;}
}class BstTree {//插入结点public Node insertBst(Node root, int key) {if (root == null) {//直接返回这个新结点//指到最后可添加位置,也是直接指向这个新节点return new Node(key);}if (key < root.key) {//往左边走root.left = insertBst(root.left, key);} else if(key > root.key) {//往右边走root.right = insertBst(root.right, key);}return root;//这里返回root的意思也就是中间的结点必须连上}//删除结点public Node deleteBST(Node root, int key) {if (root == null) {return root;}if (key < root.key) {root.left = deleteBST(root.left, key);} else if (key > root.key) {root.right = deleteBST(root.right, key);} else {//找到了这个结点if (root.left == null) {//直接返回这个结点的右结点给上一个节点return root.right;} else if (root.right == null) {return root.left;}//上面都没有进入,说明有左右子树,需要结点上一移动//先改变查找到结点的值,我们需要用它的直接后继来替换//也就是找到它右边的结点,然后不停的左边,一直到尽头root.key = minValue(root.right);//改变结点之间的连接root.right = deleteBST(root.right, root.key);}return root;}// 寻找最小值//从某个结点一直找到最左边就是最小值public int minValue(Node root) {while (root != null && root.left != null) {root = root.left;}return root.key;}//中序遍历这个结点public void inorderTraverseBst(Node root) {if (root != null) {//先打印左边inorderTraverseBst(root.left);System.out.print(root.key + " ");inorderTraverseBst(root.right);}}//查找某一个元素public Node searchBST(Node root, int key) {if (root == null || root.key == key) {return root;}if (key < root.key) {return searchBST(root.left, key);}return searchBST(root.right, key);}}public class Solution {public static void main(String[] args) {BstTree bstTree = new BstTree();Node root = null;//root在堆上就已经建立空间root = bstTree.insertBst(root, 3);bstTree.insertBst(root, 8);bstTree.insertBst(root,2);bstTree.insertBst(root,5);bstTree.insertBst(root,4);bstTree.insertBst(root,9);bstTree.insertBst(root,1);//中序遍历这片空间bstTree.inorderTraverseBst(root);System.out.println("-----------------");bstTree.deleteBST(root,2);bstTree.deleteBST(root,8);bstTree.inorderTraverseBst(root);}}
好了,说到这。
相关文章:

树之二叉排序树(二叉搜索树)
什么是排序树 说一下普通二叉树可不是左小右大的 插入的新节点是以叶子形式进行插入的 二叉排序树的中序遍历结果是一个升序的序列 下面是两个典型的二叉排序树 二叉排序树的操作 构造树的过程即是对无序序列进行排序的过程。 存储结构 通常采用二叉链表作为存储结构 不能 …...
管易云与电商平台的无代码集成:实现API连接与用户运营
管易云简介及其与电商平台的合作 金蝶管易云是金蝶集团旗下以电商为核心业务的子公司,是国内最早的电商ERP服务商之一,总部在上海,与淘宝、天猫、 京东、拼多多、抖音等300多家主流电商平台建立合作关系,同时管易云是互联网平台首…...
)
ElementUI的el-upload上传组件与表单一起提交遇到的各种问题以及解决办法(超详细,每个步骤都有详细解读)
背景: 使用ruoyi-vue进行2次开发,需要实现表单与文件上传一起提交,并且文件上传有4个,且文件校验很复杂,因此ruoyi-vue集成的上传组件FileUpload调试几天后发现真不太适用,最终选择element UI原生组件el-upload(FileUpload也是基于el-upload实现的),要实现表单与文件同…...

python flask_restful “message“: “Failed to decode JSON object: None“
1、问题表现 "message": "Failed to decode JSON object: None"2、出现的原因 Werkzeug 版本过高 3、解决方案 pip install Werkzeug2.0解决效果 可以正常显示json数据了 {"message": {"rate": "参数错误"} }...
Linux内核有什么之内存管理子系统有什么第六回 —— 小内存分配(4)
接前一篇文章:Linux内核有什么之内存管理子系统有什么第五回 —— 小内存分配(3) 本文内容参考: linux进程虚拟地址空间 《趣谈Linux操作系统 核心原理篇:第四部分 内存管理—— 刘超》 特此致谢! 二、小…...
)
【OpenHarmony内核】Harmony内核之线程操作函数(二)
文章目录 前言一、获取线程优先级二、转交控制运行权三、挂起线程3.1 线程的挂起是什么意思?3.2 函数介绍四、恢复线程五、分离指定的线程5.1 分离线程是什么意思5.2 函数介绍六、等待线程终止运行七、终止当前线程的运行八、终止指定线程的运行九、获取活跃线程数总结前言 O…...

二十五、W5100S/W5500+RP2040树莓派Pico<Modebus TCP Server示例>
文章目录 1 前言2 简介2 .1 什么是Modbus TCP?2.2 Modbus TCP指令介绍2.3 请求数据过程2.4 Modbus TCP协议优点2.5 Modbus TCP应用场景 3 WIZnet以太网芯片4 Modbus TCP示例概述以及使用4.1 流程图4.2 准备工作核心4.3 连接方式4.4 主要代码概述4.5 结果演示 5 注意…...

Android画个圆点状态灯
1、创建一个 XML 文件在 res/drawable 目录下(默认为黑色) <?xml version"1.0" encoding"utf-8"?> <shape xmlns:android"http://schemas.android.com/apk/res/android"android:shape"oval"><…...

高性能网络编程 - 解读3种线程模型
文章目录 Pre线程模型1:传统阻塞 I/O 服务模型线程模型2:Reactor 模式Reactor 模式的基本设计思想Reactor 模式中的关键组成3种典型实现单 Reactor 单线程单 Reactor 多线程主从 Reactor 多线程 小结 线程模型3:Proactor 模型 Pre 高性能网络…...
MATLAB中deconvwnr函数用法
目录 语法 说明 示例 使用 Wiener 滤波对图像进行去模糊处理 deconvwnr函数的功能是使用 Wiener 滤波对图像进行去模糊处理。 语法 J deconvwnr(I,psf,nsr) J deconvwnr(I,psf,ncorr,icorr) J deconvwnr(I,psf) 说明 J deconvwnr(I,psf,nsr) 使用 Wiener 滤波算法对…...

赛宁网安入选国家工业信息安全漏洞库(CICSVD)2023年度技术组成员单
近日,由国家工业信息安全发展研究中心、工业信息安全产业发展联盟主办的“2023工业信息安全大会”在北京成功举行。 会上,国家工业信息安全发展研究中心对为国家工业信息安全漏洞库(CICSVD)提供技术支持的单位授牌表彰。北京赛宁…...

Git系列之Git集成开发工具及git扩展使用
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是君易--鑨,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的博客专栏《Git实战开发》。🎯🎯 &a…...

selenium headless 无头模式慢
selenium设置headlessTrue发现非常慢,headlessFalse要快很多。 最后测试发现升级到selenium最新版本,selenium4.15.2。设置--headlessnew,解决了,速度正常了。 新版selenium有了两种headless模式,参见:He…...
快速修复因相机断电导致视频文件打不开的问题
3-5 本文主要解决因相机突然断电导致拍摄的视频文件打不开的问题。 在日常工作中,有时候需要使用相机拍摄视频,比如现在有不少短视频拍摄的需求,如果因电池突然断电的原因,导致拍出来的视频播放不了,这时候就容易出大…...

Ceph 笔记, ssh写入缓存
硬件建议 — Ceph 文档 写入缓存 企业级 SSD 和 HDD 通常包括断电保护功能,包括 在运行时断电时确保数据耐久性,以及 使用多级缓存来加快直接或同步写入速度。这些设备 可以在两种缓存模式之间切换 -- 刷新到的易失性缓存 具有 fsync 的持久性媒体&a…...
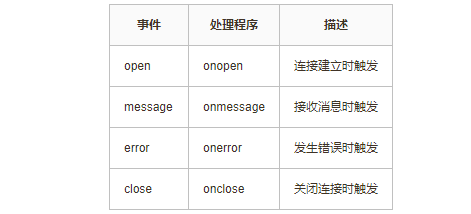
WebSocket魔法师:打造实时应用的无限可能
1、背景 在开发一些前端页面的时候,总是能接收到这样的需求:如何保持页面并实现自动更新数据呢?以往的常规做法,是前端使用定时轮询后端接口,获取响应后重新渲染前端页面,这种做法虽然能达到类似的效果&…...
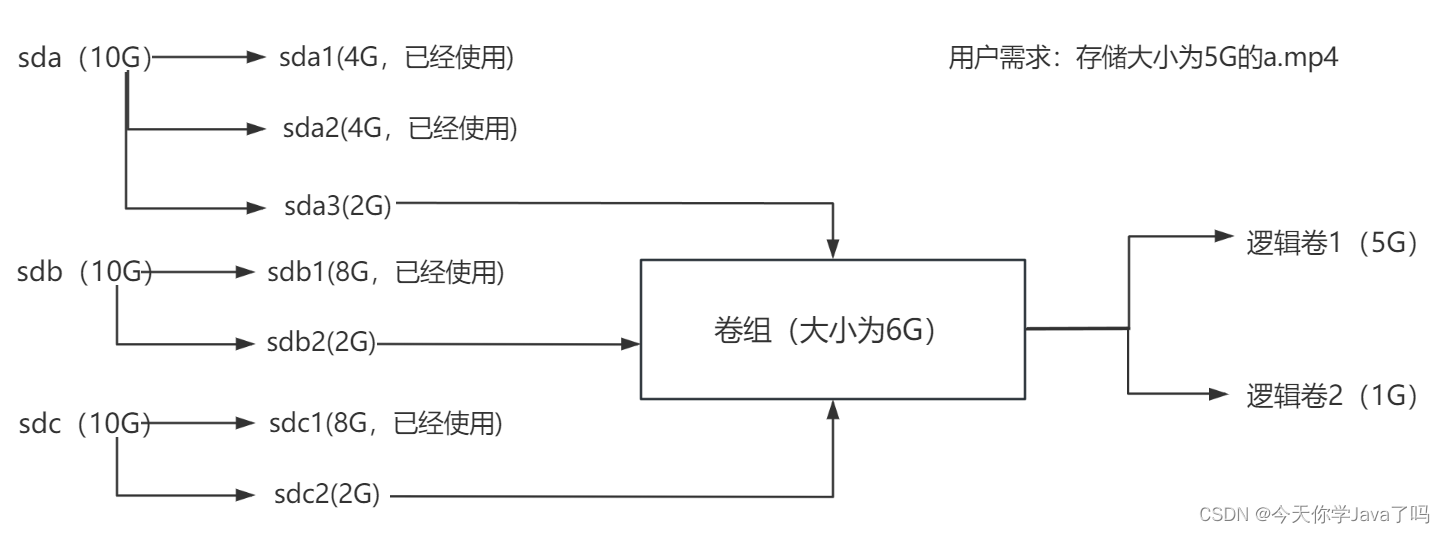
网络运维Day06-补充
文章目录 RAID磁盘阵列RAID0条带模式RAID1镜像模式RAID5高性价比模式RAID01RAID10 逻辑卷一块磁盘的使用流程逻辑卷的使用流程 制作逻辑卷步骤一:添加硬盘步骤二:分区规划步骤三:制作物理卷步骤四:制作卷组步骤五:制作…...
)
openssl+SM2开发实例一(含源码)
一、SM2算法介绍 SM2(国密算法2) 是中国国家密码管理局(CNCA)颁布的椭圆曲线密码算法标准,属于非对称加密算法。它基于椭圆曲线离散对数问题,提供了安全可靠的数字签名、密钥交换和公钥加密等功能。SM2被设…...
操作系统 | 编写内核
🌈个人主页:Sarapines Programmer🔥 系列专栏:《操作系统实验室》🔖少年有梦不应止于心动,更要付诸行动。 目录结构 1. 操作系统实验之编写内核 1.1 实验目的 1.2 实验内容 1.3 实验步骤 1.4 实验过程 …...
)
Rust逆向学习 (4)
Reverse for Struct Rust中的结构体是一个重要的内容,由于Rust中没有类的概念,因此其他编程语言中的封装、继承、多态与Rust中的表现都有较大差异。 我们使用参考书中的一个示例开始进行分析。 Struct 初始化 struct User {username: String,email: …...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
